西瓜的matlab小白级笔记——2.1 矩阵初步

matlab的数据核心为矩阵形式，想要玩转matlab，首先要熟悉矩阵的各种表示形式。

文章目录

• 一、矩阵的输入
• • 1.标量
  • 2.向量
  • 3.二维矩阵
  • 4.高维矩阵
• 二、矩阵的数据性质

一、矩阵的输入

• 最常见的矩阵是二维矩阵，分为行和列两个维度，如果一个矩阵有$m$行$n$列，我们$m\times n$为矩阵的大小。
• 当矩阵的维度大于等于3时，我们称其为多维矩阵。

对于不同的矩阵，我们举例说明：

1.标量

当矩阵的大小为$1\times 1$时，这样的矩阵就是一个数，我们称之为标量。想要在matlab中输入一个标量，有两种方式，分别是给变量赋值或者直接输入值。

x=159.13 %在命令行窗口中给变量x赋值152 %或者直接输入数字

点击enter回车后输出结果为

从结果中可以看出，当赋值给变量时，matlab会即时返回变量的值；当直接输入数值时，会将值赋给名为ans（其名为预定义变量answer）的变量。同时，在红框中的工作区可以查看目前所有变量的赋值情况。

2.向量

当矩阵大小为$1\times n$或者$n\times 1$时，我们将其称之为向量，前者称为行向量（因为它只有一行），后者称为列向量。
在matlab中，我们使用逗号或空格来分割列，使用分号或回车号分割行，并用一对方括号[ ]框起来，如果我们想输入
r = ( 3 4 5 ) , c = ( 3 4 5 ) r=\\begin{pmatrix}3&4&5\\end{pmatrix}, c=\\begin{pmatrix}3\\\\4\\\\5\\end{pmatrix} r=(3​4​5​),c= ​345​ ​

% 这是行向量，意为rowr=[3,4,5] r=[3 4 5]%这是列向量，意为colc=[3;4;5]c=[345] %值得注意的是，在打回车时，请同时按下enter+shift，不然会直接输出结果%如果命令比较长的话，在回车之前加入...以分割长命令到多行，例如:A=[145644646,6464661,66161611,...464616,1616446]

如果想看到自己输入的变量内都含有什么元素，可以在命令行窗口输入变量的名称，例如

>>c >>r %直接输入变量名称c和r

除此之外，还可以双击点击工作区内的变量，获得变量内的视图：

3.二维矩阵

如果我们想输入
A = ( 7 6 3 8 9 5 ) A=\\begin{pmatrix}7 &6&3\\\\8&9&5\\end{pmatrix} A=(78​69​35​)
和输入向量同理

%以下四种方式都是正确的A=[7 6 3;8 9 5]A=[7,6,3;8,9,5]A=[7 6 38 9 5]A=[7,6,38,9,5]

其中第一种方式的输出结果为

除此之外，还可以依次给矩阵内的各个元素分配数值，例如：

A(1,1)=7,A(1,2)=6,A(1,3)=3,A(2,1)=8,A(2,2)=9,A(2,3)=5

或者

 A(1,1)=7;A(1,2)=6;A(1,3)=3;A(2,1)=8;A(2,2)=9;A(2,3)=5

以上两种方法的区别在于使用逗号分隔命令还是使用分号分隔命令。事实上，在matlab中，输入命令会默认即时输出结果。如果在命令的结尾加上分号，那么结果就不会即时输出，也就是说，变量被赋值了但是不会显示在命令行窗口中。上面使用分号分割命令之后，最后一个命令并没有使用分号结尾，因此只会在最后一个命令后输出结果。
当赋值的变量比较多时，这种方法能够让我们的界面显得不会过于杂乱。

4.高维矩阵

对于高维矩阵，我们无法简单地使用行和列进行表示，由此，我们需要使用索引法，分为矩阵索引和线性索引。以三维矩阵为例，我们可以想象一个立方体，使用两种方式对其中的元素进行编号处理：

• 矩阵索引
  
  如图所示，我们将三维矩阵视为一个立体空间下的立方体，矩阵索引的第一个数字代表该点在第一维$x$中的位置，第二个数字代表该点在第二维度$y$中的位置，而第三个数值代表在第三维$z$中的位置（可以视为第几个页面），并以此推广到$n$维。

• 线性索引
  
  按照从上往下，从左往右的顺序，依次给矩阵的各个元素进行编号，便称之为线性索引。（顺序要记住，不然输入错的时候只能像本瓜一样哭晕在电脑前）。

如果我们要输入一个三维矩阵，可以给各个元素赋值如下：

B(1,1,1)=3;B(1,2,1)=6;B(1,1,2)=5;B(2,1,2)=6;B(2,1,3)=9;B(2,2,3)=4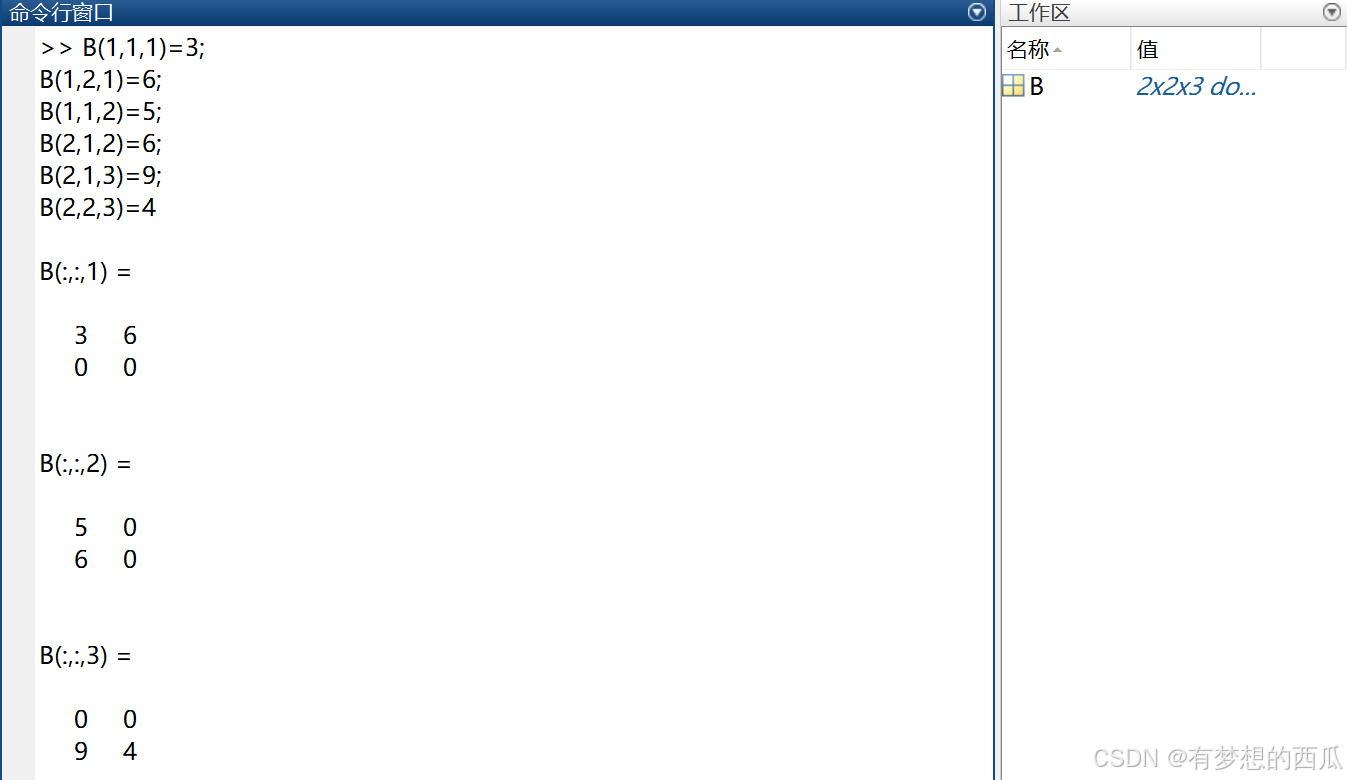

我们的第三维有三个数值，也就是说第三维有三页矩阵，而可怜的matlab只是个二维生物，没法直接表示三维的矩阵，只能拆成三页来显示。
值得注意的是，当没有给矩阵的某个位置赋值时，该值默认为0.
而B(:,:,1)的意思是，取该页的所有行和所有列，使用冒号的地方即为取该维度的所有值，例如：B(1,:,3)即取第三页的第一行（包含所有列）。
通过这个方法，我们也可以将多个低维矩阵合成一个高一维的矩阵，例如：

 A=[2,5,6;8,4,0];B=[87,51,32;45,952,51]; U(:,:,1)=A;U(:,:,2)=B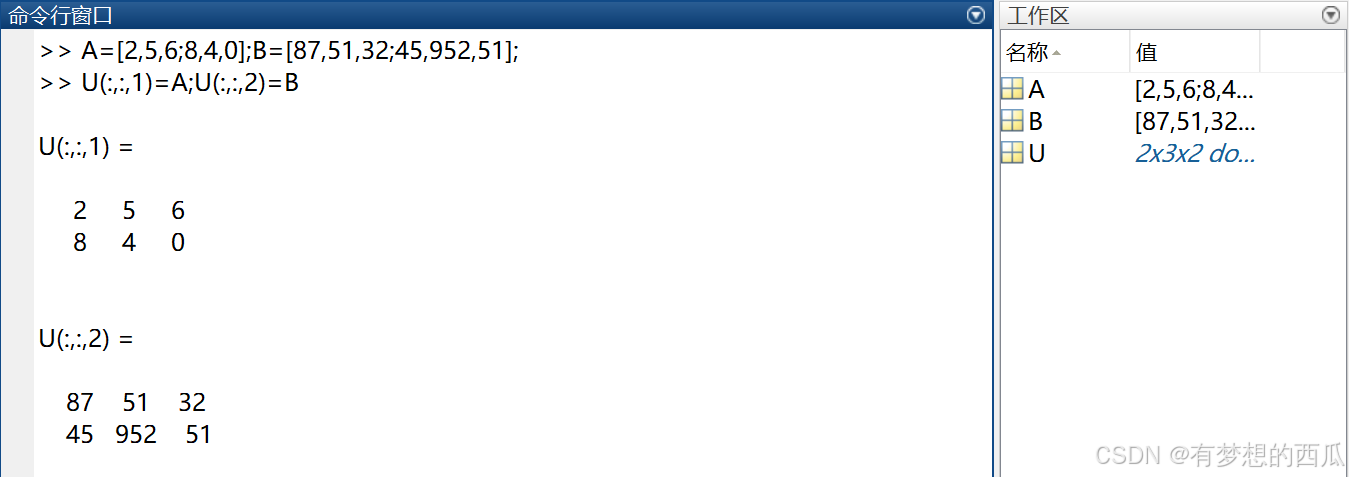

我们将A和B分别赋值给了新矩阵U的第一页和第二页，构成三维矩阵。

二、矩阵的数据性质

以上是矩阵中常用的命令。

往期回顾：
西瓜的Matlab小白级笔记——1.1 初见matlab
西瓜的matlab小白级笔记——1.2 matlab的下载