【B题解题思路第二弹】2025创新杯（钉钉杯）数学建模B题解题思路+可运行代码参考（无偿分享）

技术文档

注：该内容由“数模加油站”原创，无偿分享，可以领取参考但不要利用该内容倒卖，谢谢！

B 题道路路面维护需求综合预测

问题A 路面维护需求预测回归分析问题

在本次研究中，我们针对道路维护需求的预测和优先级划分问题，提出了一种基于特征重要性分析与聚类算法的综合方法。首先，通过构建预测模型（如随机森林、XGBoost等），对每条道路的维护需求进行了预测，并利用模型自带的特征重要性评分，识别了影响道路维护需求的关键特征。接着，我们基于这些关键特征，使用K均值聚类、层次聚类和自组织映射（SOM）三种聚类算法对道路段进行了分组，形成了高优先级、中优先级和低优先级的维护分类。为了评估聚类效果，使用了轮廓系数和DB指数作为聚类质量的衡量标准。通过比较不同算法的评估结果，最终为交通管理部门提供了一种科学的道路维护优先级划分策略。

此外，结合SHAP值分析，我们进一步揭示了每个特征对道路维护需求预测的贡献，为特征选择和聚类优化提供了数据支持。最终，聚类结果的可视化帮助我们直观展示了不同优先级路段的分布，为后续的资源分配和道路养护策略提供了有效依据。

本研究的方法不仅提高了道路维护资源的分配效率，还为交通管理提供了可操作性的决策支持，具有较强的实践意义和应用前景。

问题1思路框架：

一、问题描述与建模目标

本赛题的目标是通过多维度的数据特征（如路面状况指数PCI、年平均日交通量AADT、沥青类型等）预测某条道路是否需要进行维护。该问题的背景与需求明确了模型应当具备较强的预测能力，并且能够准确反映出哪些特征对维护需求有着直接的影响。道路的维护需求不仅仅是单一维度特征所决定的，而是受到诸如路面损坏程度、交通量、气候条件等多种因素的共同影响，因此，构建一个能够综合考虑这些复杂因素的数学模型是非常重要的。

具体而言，赛题要求我们预测目标变量“是否需要维护”，这是一个二分类问题，标签为1表示需要维护，标签为0表示不需要维护。模型构建不仅要求有较高的预测准确度，还要求对每个特征在预测中的贡献进行详细分析，以便为后续的维护策略优化提供依据。

我们需要明确该问题的目标函数，假设数据中包含了多个影响道路维护需求的特征，这些特征可以通过数学模型进行学习与关联，从而预测出目标变量。在模型构建过程中，除了对数据进行清洗与预处理外，特征选择、模型的选择与评估将是至关重要的步骤。针对这个任务，我们将采用机器学习中的二分类方法，并通过精确度、召回率与F1值来评估模型性能。同时，利用SHAP值来分析每个特征的重要性，帮助我们理解模型的决策过程。

二、数据分析与预处理

2.1 特征工程

首先，对于类别型特征（如道路类型、沥青类型），我们采用序列编码的方法进行处理，避免造成维度灾难，同时不会影响假设检验的效果。这种方法能够有效地将类别特征引入模型，避免模型因未能处理类别变量而产生偏差。

对于数值型特征（如PCI、AADT、Rutting、IRI等），标准化和归一化是常用的处理方式。标准化将数据变换为均值为0、方差为1的分布，这对于大多数机器学习算法尤其重要，因为很多算法依赖于数据的尺度一致性。

此外，针对包含时间信息的特征（如上次大修年份），我们可以通过计算当前年份与大修年份的时间差，转化为“距离最后一次大修的年数”这一特征。这种特征反映了时间对于道路维护需求的影响，可能会对预测结果产生显著影响。

2.2 数据分析

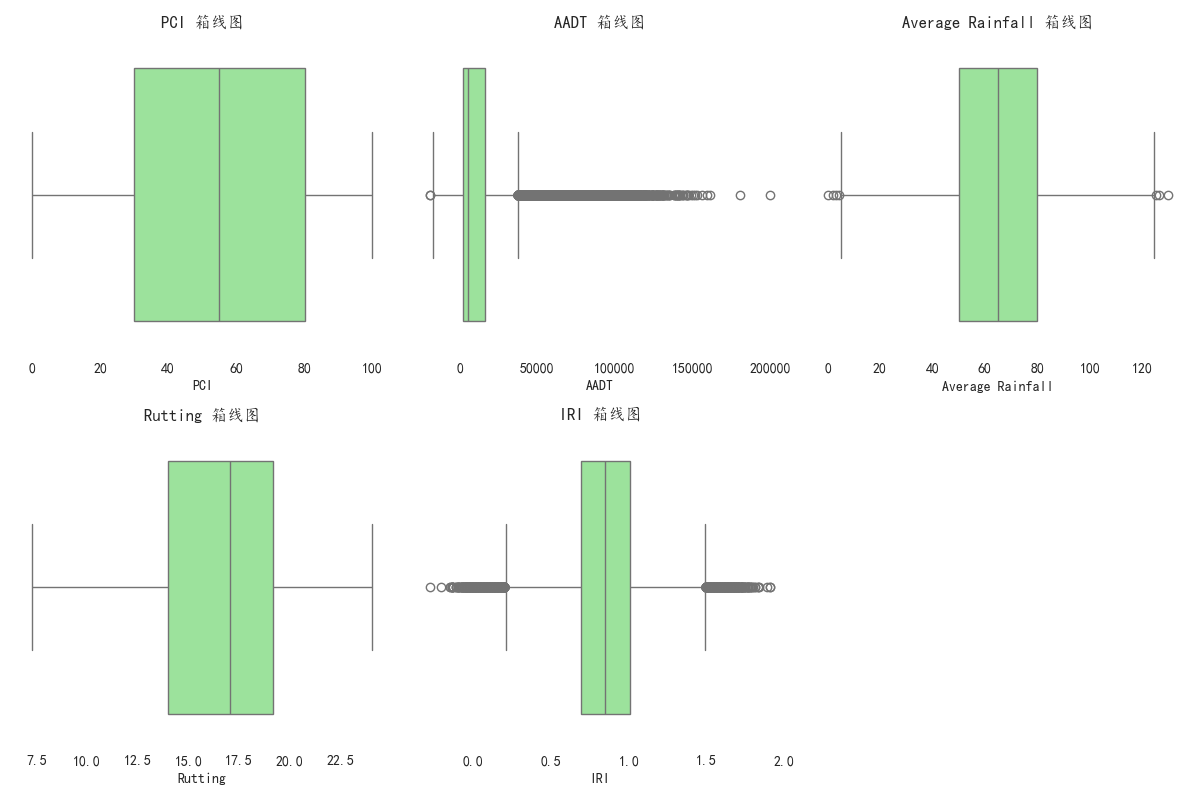
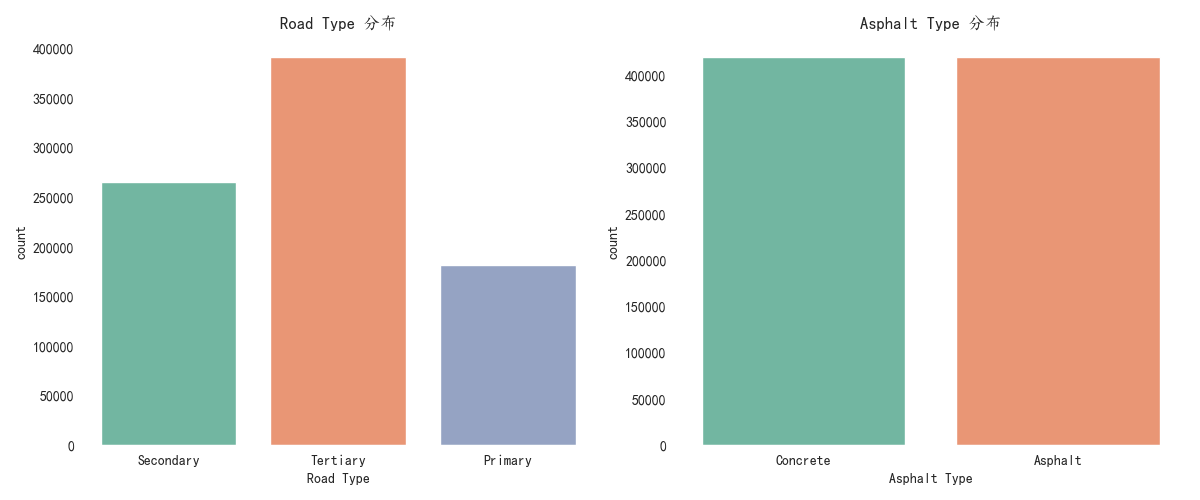
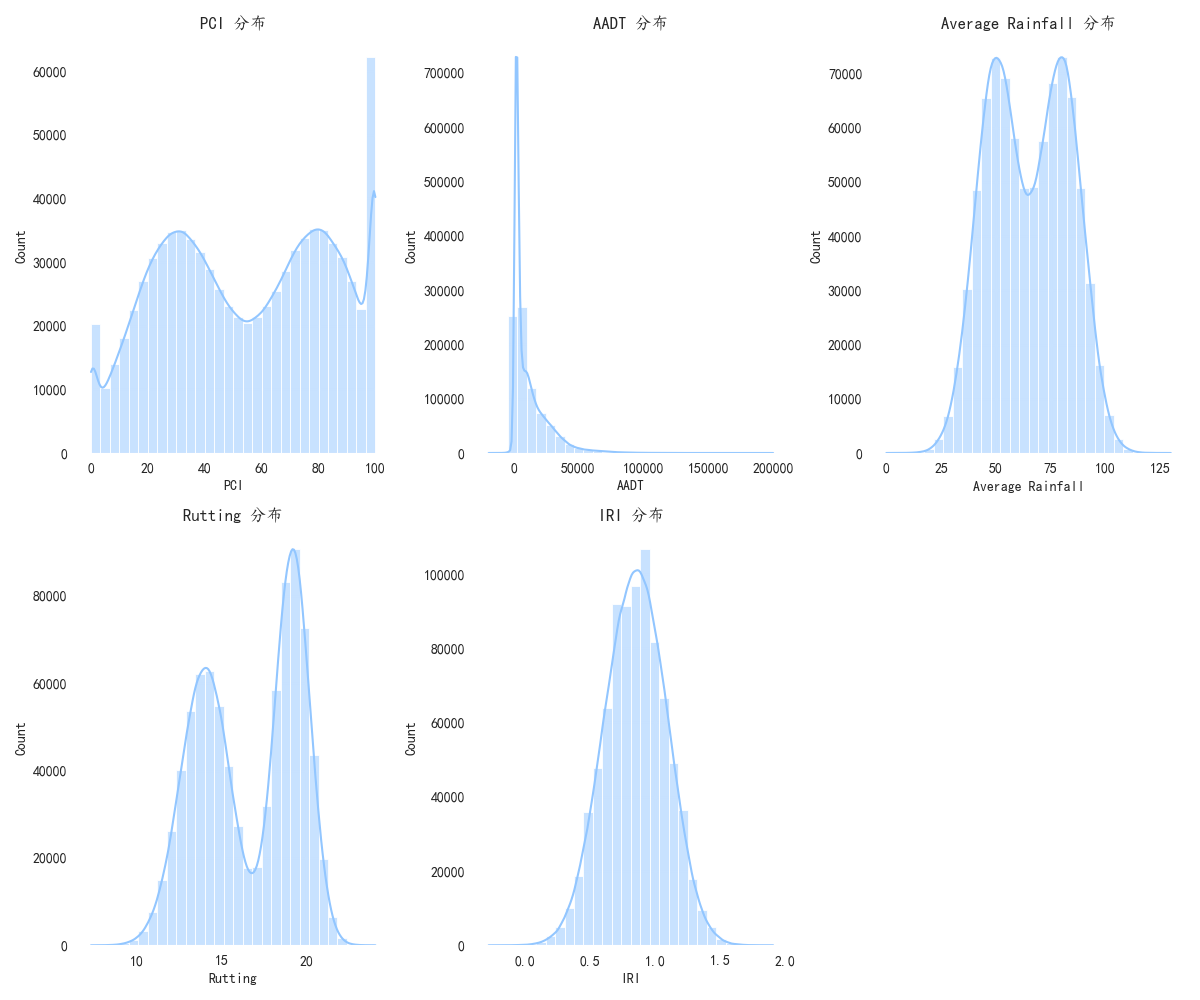
数据探索与可视化是建立在直觉上的第一步。在这一步，我们可以通过散点图、箱型图、相关热力图等方法，检查特征与目标标签之间的关系。例如，可以绘制PCI与是否需要维护之间的散点图，来观察PCI值与道路是否需要维护之间的关系。一般来说，较低的PCI值可能表示路面状况较差，因此较高的PCI值可能会与“不需要维护”标签更强的相关性。

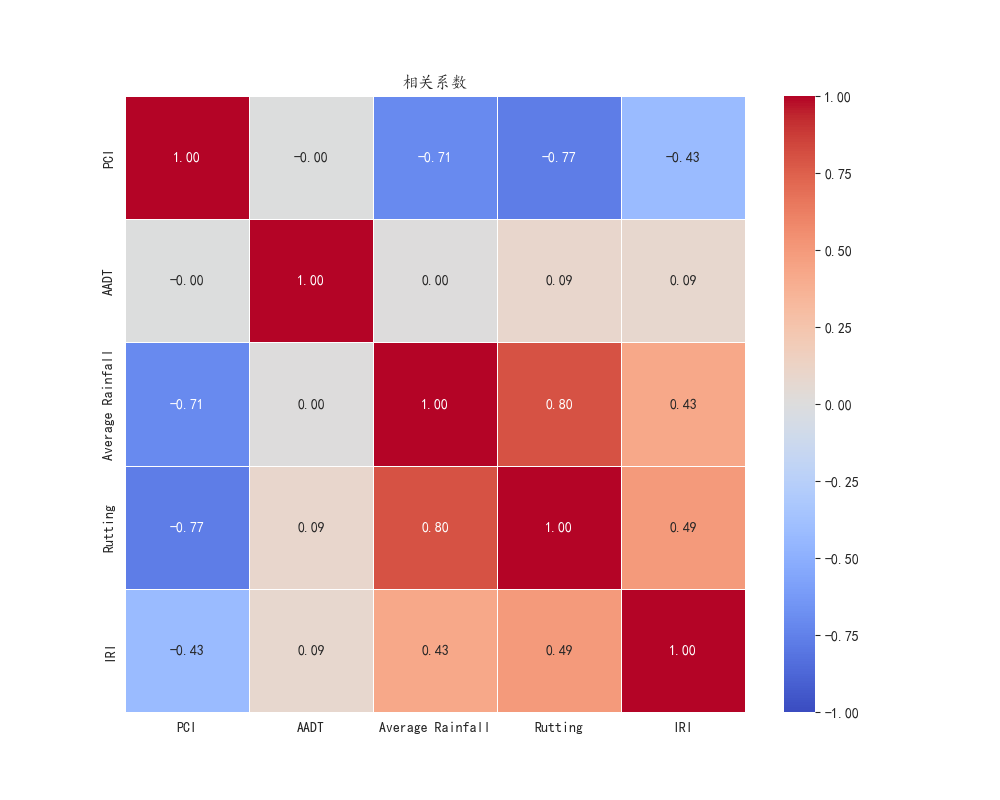
此外，使用相关性分析来探索特征之间的相互关系是非常有用的。例如，通过计算皮尔逊相关系数（）来量化数值型特征之间的相关性。强相关的特征可以帮助我们进一步精简模型，去除冗余特征。对于类别型特征，可以使用卡方检验等统计方法来评估它们与目标标签之间的关联强度。

2.3 假设检验

假设检验是一种统计学方法，用于评估样本数据是否支持某个假设。假设检验分为两种类型：

单尾检验：检验某一方向上的假设（例如，“变量A是否大于B”）。
双尾检验：检验两种不同假设（例如，“变量A与B是否相等”）。

在我们的任务中，我们希望检验每个特征与目标变量（是否需要维护）之间是否存在显著的统计关系，从而帮助我们判断哪些特征对维护需求预测的影响较大。

根据特征的类型，我们将选择合适的假设检验方法。特征可以分为数值型特征（如PCI、车辙深度Rutting等）和类别型特征（如道路类型、沥青类型等）。针对不同类型的特征，假设检验方法有所不同。

2.3.1 数值型特征与目标变量（双样本t检验）

对于数值型特征（如PCI、车辙深度、AADT等），我们可以使用独立样本t检验（Independent Two-Sample t-test）来检验特征值在不同目标类别下（是否需要维护与不需要维护）是否有显著差异。具体步骤如下：

零假设（H0）：该特征在需要维护的道路和不需要维护的道路之间没有显著差异。
备择假设（H1）：该特征在需要维护的道路和不需要维护的道路之间存在显著差异。

假设检验的公式：

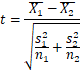
其中，和分别表示两组数据（需要维护与不需要维护）均值，和是两组数据的方差，和是两组样本的数量。通过计算得到的t 值与临界值进行比较，若t值超过临界值，则拒绝零假设，表示该特征与目标变量之间存在显著差异。

2.3.2 类别型特征与目标变量（卡方检验）

对于类别型特征（如道路类型、沥青类型等），我们可以使用卡方检验（Chi-Square Test）来检验类别特征与目标变量之间的独立性。卡方检验常用于检验观察频数与理论频数之间的差异是否显著，适用于类别型变量。

零假设（H0）：类别特征与目标变量之间独立，即该类别特征对目标变量没有显著影响。
备择假设（H1）：类别特征与目标变量之间不独立，即该类别特征与目标变量之间有显著关联。

卡方检验的公式为：

其中，表示观察到的频数，Ei 表示期望的频数，k 是类别的数目。计算出的卡方值与临界值比较，如果卡方值大于临界值，则拒绝零假设，表示该类别特征与目标变量之间存在显著相关性。

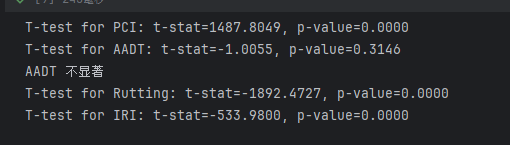
根据每个特征的假设检验结果，我们可以评估哪些特征对模型的预测结果有显著影响。例如，如果PCI值在需要维护和不需要维护的路段之间的差异显著，那么我们可以认为PCI是影响维护需求的重要特征。如果卡方检验结果显示沥青类型与是否需要维护之间存在显著关系，我们也应该将沥青类型作为关键特征之一。

p值的判断：通常，我们使用显著性水平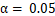作为判断标准。当p值小于0.05时，拒绝零假设，认为该特征与目标变量之间存在显著关系；当p值大于0.05时，则无法拒绝零假设，认为该特征与目标变量之间的关系不显著。
特征选择：基于假设检验的结果，特征选择可以依据显著性来筛选出对目标变量影响较大的特征。这有助于减少模型的复杂度，提高模型的准确性与解释性。

数学模型构建：

三、模型的选择与构建

在本任务中，我们需要构建一个二分类模型，来预测每个道路段是否需要维护。为了实现这个目标，我们可以选择多种机器学习算法，这些算法具有不同的特性，能够在不同的数据环境下表现出不同的优缺点。本文将详细介绍几种常见的分类算法，包括决策树、XGBoost、随机森林和逻辑回归，并分析它们各自的适用场景、优缺点及其在本赛题中的应用。

3.1 决策树

决策树是一种非常直观的分类算法，属于树形结构的模型，通过树的结构进行决策。它通过一系列的决策节点（decision nodes）将数据划分成若干子集，每个叶节点（leaf node）对应一个类别标签。决策树通过“分裂”每个特征的值来使得每个分裂后的子集变得更为纯粹，最终将每个数据样本归类到其所属类别。

在本赛题中，决策树可以用于构建一个初步的模型来了解数据中各个特征对维护需求的影响。由于其较强的解释性，决策树能够帮助我们直观地理解特征如何影响道路是否需要维护的预测。此外，我们可以使用剪枝（pruning）技术来控制树的深度，避免过拟合。

模型公式：

决策树的构建过程基于信息增益（Information Gain）或者基尼指数（Gini Index），其目标是最大化每次分裂后的纯度。信息增益的计算公式为：

其中，表示数据集D的熵值，是根据特征A的取值划分后的子集，是子集的样本量，是整个数据集的样本量。

3.2 XGBoost

XGBoost是一种基于梯度提升决策树（GBDT）方法的集成学习算法。XGBoost通过将多个弱分类器（通常是决策树）组合起来形成一个强分类器，逐步优化误差，最终获得较为精准的分类结果。XGBoost在许多机器学习竞赛中表现优异，尤其擅长处理复杂的特征数据。

模型公式：

XGBoost采用了加法模型（Additive Model）和梯度提升（Gradient Boosting）的思想，具体更新公式为：

其中，是第棵树的预测结果，是第棵树的基学习器（通常是回归树），是树的权重，是学习率。

3.3 随机森林（Random Forest）

随机森林是一种基于集成学习的算法，利用多个决策树来进行分类预测。每棵决策树都在不同的训练数据子集上进行训练，并通过投票机制得到最终的预测结果。

随机森林的核心思想是对多个决策树进行集成，每棵树的输出进行投票或平均，最终得到结果。公式为：

其中，是最终的预测结果，是树的数量，是第t 棵树的预测。

3.4 逻辑回归（Logistic Regression）

逻辑回归是一种基于线性回归思想的分类模型，适用于处理二分类问题。逻辑回归通过sigmoid函数将线性回归的输出映射到[0, 1]之间，从而得到样本属于某一类别的概率。

在本赛题中，如果特征与维护需求之间的关系较为简单且接近线性，逻辑回归可以作为一个基准模型进行快速的预测和分析。

逻辑回归的核心是通过sigmoid函数对线性模型的输出进行映射：

其中，为模型参数，为输入特征，为偏置项，为给定输入特征时，样本属于类别1的概率。

四、特征重要性分析与结果展示

4.1 SHAP值分析

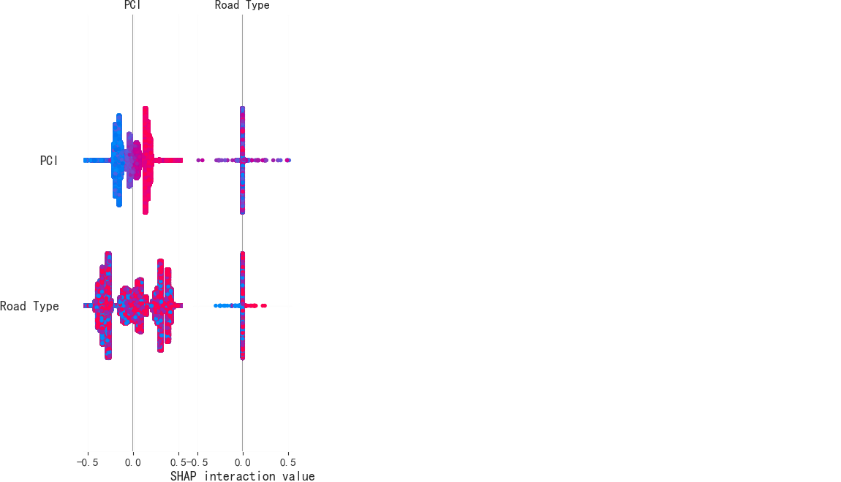
在完成模型训练后，可以使用SHAP（SHapley Additive exPlanations）值分析来量化每个特征对预测结果的贡献。SHAP值是一种基于博弈论的解释方法，它能够准确地衡量每个特征对模型预测结果的边际贡献。

通过SHAP值分析，我们能够深入理解哪些特征对维护需求预测最为关键。例如，PCI值、车辙深度和IRI等特征可能对是否需要维护的预测产生较大影响，而如沥青类型或降雨量等特征则可能对一些道路类型的维护需求产生较小的影响。通过这种特征重要性分析，交通管理部门能够根据特征的优先级，制定更为合理的道路维护策略

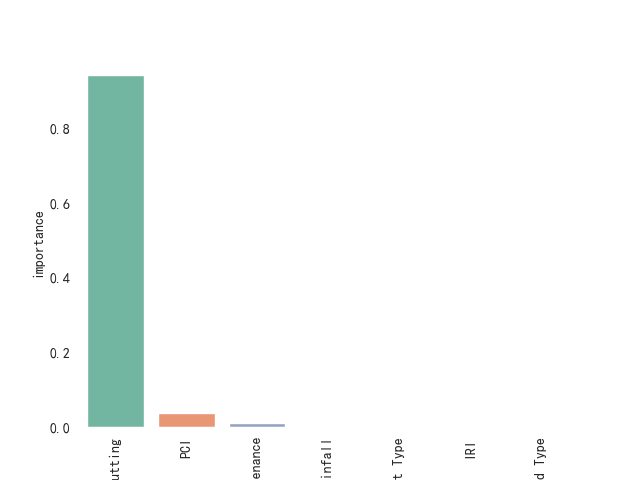
Python代码：

#%%import pandas as pdimport numpy as npimport matplotlib.pyplot as pltimport seaborn as snsfrom sklearn.model_selection import train_test_splitfrom sklearn.preprocessing import StandardScaler, LabelEncoderfrom sklearn.ensemble import RandomForestClassifierfrom sklearn.metrics import accuracy_score, recall_score, f1_score, confusion_matrixfrom scipy.stats import ttest_ind, chi2_contingencyimport shap#%%plt.rcParams[\'font.sans-serif\'] = [\'Kaiti\']plt.rcParams[\'axes.unicode_minus\'] = Falseplt.style.use(\'seaborn-v0_8-pastel\')#%%data = pd.read_csv(\'./数据挖掘：train_data.csv\')data.describe()#%%num_features = [\'PCI\', \'AADT\', \'Average Rainfall\', \'Rutting\', \'IRI\']plt.figure(figsize=(12, 10))for i, feature in enumerate(num_features, 1): plt.subplot(2, 3, i) sns.histplot(data[feature], kde=True, bins=30) plt.title(f\'{feature} 分布\')plt.tight_layout() plt.savefig(\'./pic/histplot.png\',transparent=True)#%%plt.figure(figsize=(12, 8))for i, feature in enumerate(num_features, 1): plt.subplot(2, 3, i) sns.boxplot(x=data[feature], color=\"lightgreen\") plt.title(f\'{feature} 箱线图\')plt.tight_layout()plt.savefig(\'./pic/boxplot.png\',transparent=True) #%%categorical_features = [\'Road Type\', \'Asphalt Type\']plt.figure(figsize=(12, 5))for i, feature in enumerate(categorical_features, 1): plt.subplot(1, 2, i) sns.countplot(x=data[feature], palette=\'Set2\') plt.title(f\'{feature} 分布\') plt.tight_layout()plt.savefig(\'./pic/countplot.png\',transparent=True)#%%corr_matrix = data[num_features].corr()plt.figure(figsize=(10, 8))sns.heatmap(corr_matrix, annot=True, cmap=\"coolwarm\", linewidths=0.5, fmt=\".2f\", vmin=-1, vmax=1)plt.title(\"相关系数\")plt.savefig(\'./pic/heatmap.png\',transparent=True)#%%X = data.drop([\'Segment ID\', \'Needs Maintenance\'], axis=1) # 去掉路段ID和目标标签y = data[\'Needs Maintenance\'] # 目标变量X#%%for feature in num_features: class_0 = X[y == 0][feature] class_1 = X[y == 1][feature] # 进行独立样本t检验 t_stat, p_value = ttest_ind(class_0, class_1) print(f\'T-test for {feature}: t-stat={t_stat:.4f}, p-value={p_value:.4f}\') # 判断p值是否小于0.05 if p_value >= 0.05: print(f\'{feature} 不显著\') num_features.pop(num_features.index(feature)) X = X.drop([feature], axis=1)#%%categorical_features = [\'Road Type\', \'Asphalt Type\'] for feature in categorical_features: contingency_table = pd.crosstab(X[feature], y) chi2_stat, p_value, dof, expected = chi2_contingency(contingency_table) print(f\'Chi-Square test for {feature}: chi2-stat={chi2_stat:.4f}, p-value={p_value:.4f}\') # 判断p值是否小于0.05 if p_value >= 0.05: print(f\'{feature} 不显著\') X = X.drop([feature], axis=1)#%%label_encoder = LabelEncoder() # 对\'Road Type\'和\'Asphalt Type\'进行标签编码X[\'Road Type\'] = label_encoder.fit_transform(X[\'Road Type\'])X[\'Asphalt Type\'] = label_encoder.fit_transform(X[\'Asphalt Type\']) scaler = StandardScaler()X[num_features] = scaler.fit_transform(X[num_features]) # 6. 数据划分：训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)#%%from sklearn.tree import DecisionTreeClassifierfrom xgboost import XGBClassifierfrom sklearn.linear_model import LogisticRegression models = { \"Random Forest\": RandomForestClassifier(n_estimators=100, random_state=42), \"Decision Tree\": DecisionTreeClassifier(random_state=42), \"Logistic Regression\": LogisticRegression(random_state=42), \"XGBoost\": XGBClassifier(random_state=42)} # 存储每个模型的评估结果results = [] # 训练并评估每个模型for model_name, model in models.items(): # 训练模型 model.fit(X_train, y_train) # 预测 y_pred = model.predict(X_test) # 计算评估指标 accuracy = accuracy_score(y_test, y_pred) recall = recall_score(y_test, y_pred) f1 = f1_score(y_test, y_pred) # 存储结果 results.append({ \"Model\": model_name, \"Accuracy\": accuracy, \"Recall\": recall, \"F1 Score\": f1 }) # 8. 将结果存储到表格中results_df = pd.DataFrame(results)results_df#%%results_df.to_csv(\'./model_comparison_results.csv\', index=False)#%%model = DecisionTreeClassifier(random_state=42)model.fit(X_train, y_train)y_pred = model.predict(X_test)cm = confusion_matrix(y_test, y_pred)sns.heatmap(cm, annot=True, fmt=\"d\",)plt.title(\'混淆矩阵\')plt.savefig(\'./pic/confusion_matrix.png\',transparent=True)#%%explainer = shap.TreeExplainer(model)shap_values = explainer.shap_values(X_train) #%%shap.summary_plot(shap_values, X_train, show=False)plt.savefig(\'./pic/shap_values.png\',transparent=True)#%%feature_importance = pd.DataFrame(model.feature_importances_, index=X_train.columns, columns=[\"importance\"]).sort_values(\"importance\", ascending=False)sns.barplot(x=feature_importance.index, y=feature_importance[\'importance\'], palette=\'Set2\')plt.xticks(rotation=90)plt.savefig(\'./pic/feature_importance.png\',transparent=True)#%% #%%

后续都在“数模加油站”......