【动态规划】【简单多状态 dp 问题】按摩师、打家劫舍、删除并获得点数、粉刷房子

文章目录

• 1. 按摩师
• • 算法原理
  • 代码编写
• 2. 打家劫舍 II
• • 题目分析
  • 算法原理
  • 代码编写
• 3. 删除并获得点数
• • 题目解析
  • 预处理
  • 算法原理
  • 代码编写
• 4. 粉刷房子
• • 算法原理
  • 代码编写

1. 按摩师

面试题 17.16. 按摩师

算法原理

1. 确定状态表示
   • dp[i] 表示：选择到 i 位置的时候，此时的最长预约时长

分析细节：
当面对一个预约的时候，可能必选（f），也可能必不选（g）

• f[i] 表示：选择到 i 的时候，nums[i] 必选，此时的最长预约时长
• g[i] 表示：选择到 i 的时候，nums[i] 不选，此时的最长预约时长

2. 状态转移方程

• 当 i 必选的时候，那么 i-1 就是必不选，此时 f[i] = g[i-1] + nums[i]
• 当 i 不选的时候，那么 i-1 可以选也可不选，此时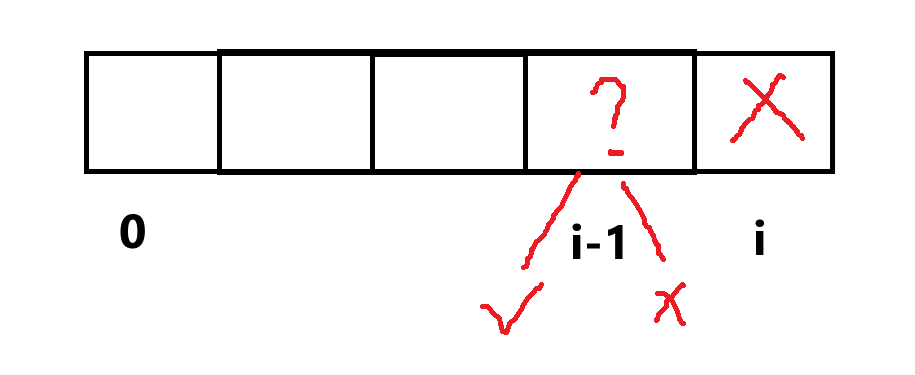
  • i-1 选，g[i] = f[i-1]
  • i-1 不选，g[i] = g[i-1]
  • 所以 g[i] = max(f[i-1], g[i-1])

3. 初始化

   • 直接初始化 f[0] = nums[0]；g[0] = 0

4. 填表顺序

   • 从左往右，两个表一起填

5. 返回值

   • 最终结果要么是最后一个位置选，要么就是不选
   • 返回 max(f[n-1], g[n-1])

代码编写

public int massage(int[] nums) { int n = nums.length; if(n == 0) return 0; //处理边界条件  int[] f = new int[n]; int[] g = new int[n]; f[0] = nums[0]; for (int i = 1; i < n; i++) { f[i] = g[i-1] + nums[i]; g[i] = Math.max(f[i-1], g[i-1]); } return Math.max(g[n-1], f[n-1]); }

2. 打家劫舍 II

213. 打家劫舍 II

题目分析

通过分类讨论，把环形的问题，转化成两个线性的“按摩师”

我们把第一个位置当做主要分析对象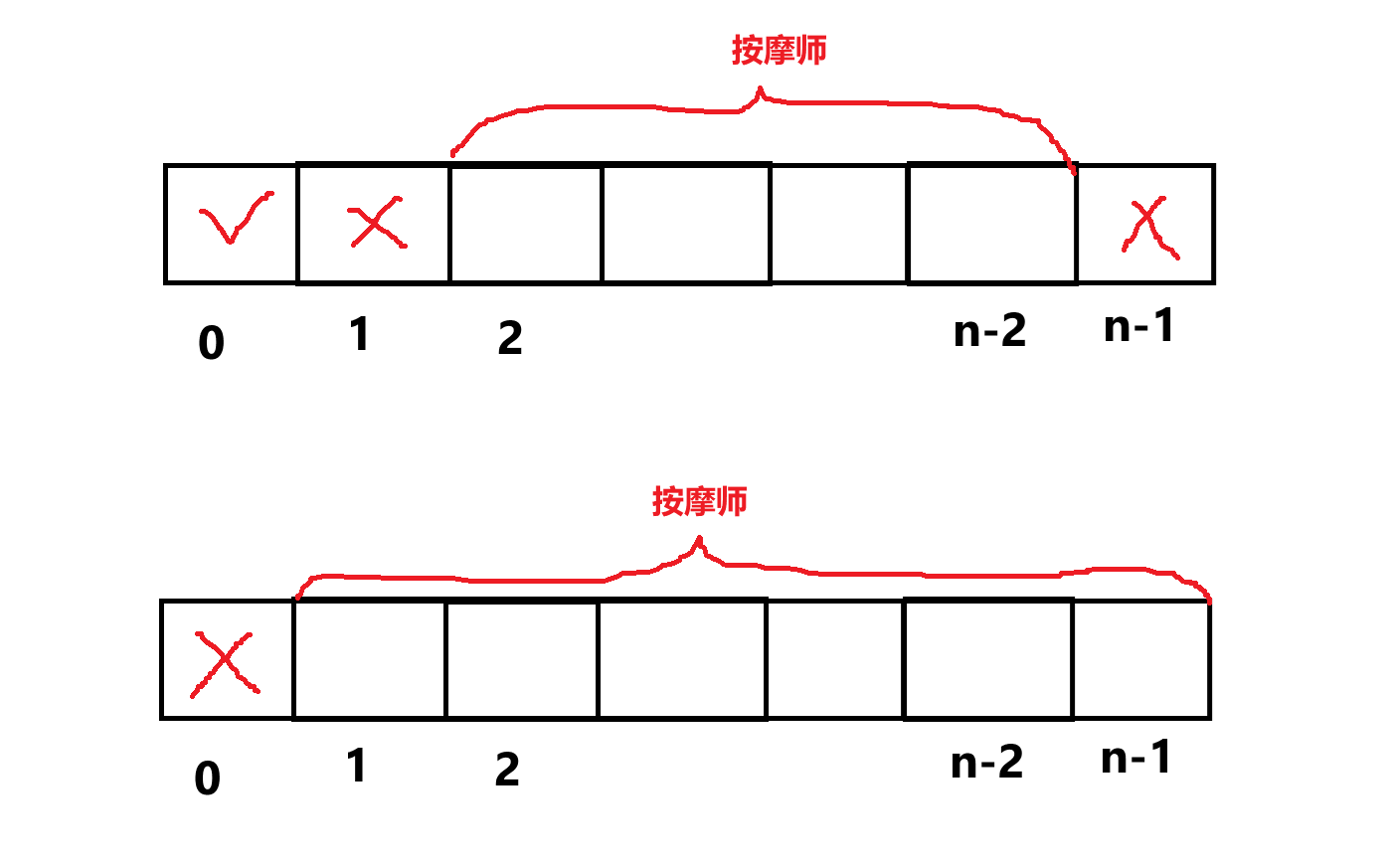

• 当第一个位置偷的时候，此时第二个位置和最后一个位置就偷不了了，相当于在 [2, n-2] 之间做一个上一题的按摩师问题
• 当第一个位置不偷的时候，就相当于在 [1, n-1] 之间做一个按摩师问题

算法原理

1. 确定状态表示

   • f[i] 表示：偷到 i 位置时，偷 nums[i]，此时的最大金额
   • g[i] 表示：偷到 i 位置时，不偷 nums[i]，此时的最大金额

2. 状态转移方程

• 当 i 必选的时候，那么 i-1 就是必不选，此时 f[i] = g[i-1] + nums[i]
• 当 i 不选的时候，那么 i-1 可以选也可不选，此时
  • i-1 选，g[i] = f[i-1]
  • i-1 不选，g[i] = g[i-1]
  • 所以 g[i] = max(f[i-1], g[i-1])

3. 初始化

   • 直接初始化 f[0] = nums[0]；g[0] = 0

4. 填表顺序

   • 从左往右，两个表一起填

5. 返回值

   • 最终结果要么是最后一个位置选，要么就是不选
   • 返回 max(f[n-1], g[n-1])

代码编写

public int rob(int[] nums) { int n = nums.length; return Math.max(nums[0] + rob1(nums, 2, n-2), rob1(nums,1, n-1)); } public int rob1(int[] nums, int left, int right){ //处理边界情况，这个房间不存在  if(left > right) return 0; //1. 创建 dp 表  int n = nums.length; int[] f = new int[n]; int[] g = new int[n]; //2. 初始化  f[left] = nums[left]; //3. 填表  for (int i = left + 1; i <= right; i++) { f[i] = g[i-1] + nums[i]; g[i] = Math.max(g[i-1], f[i-1]); } return Math.max(f[right], g[right]); }

• 因为“按摩师”要用很多次，所以可以把它封装成一个函数
• 初始化的时候不再是从 0 开始填表了，而是从 left
• 返回值是最后一个位置，也就是 right 位置

3. 删除并获得点数

740. 删除并获得点数

题目解析

这题其实和“打家劫舍”问题很像，取完一个数之后，就不能取相邻的数了，还要取的值最大

但这里的数的排列，不是相邻的，所以我们创建一个数组 arr[i]，表示这 i 这个数出现的总和

• 这样，arr[i] 就变成了符合打家劫舍问题的格式了。

预处理

将数组中的数，统计到 arr 中。然后在 arr 中做一次“打家劫舍”问题即可

算法原理

1. 确定状态表示

   • f[i] 表示：选到 i 位置的时候，nums[i] 必选，此时能获得的最大点数
   • g[i] 表是，选到 i 位置的时候，nums[i] 不选，此时能获得的最大点数

2. 状态转移方程

• 当 i 必选的时候，那么 i-1 就是必不选，此时 f[i] = g[i-1] + nums[i]
• 当 i 不选的时候，那么 i-1 可以选也可不选，此时
  • i-1 选，g[i] = f[i-1]
  • i-1 不选，g[i] = g[i-1]
  • 所以 g[i] = max(f[i-1], g[i-1])

3. 初始化

   • 直接初始化 f[0] = arr[0]；g[0] = 0

4. 填表顺序

   • 从左往右，两个表一起填

5. 返回值

   • 最终结果要么是最后一个位置选，要么就是不选
   • 返回 max(f[n-1], g[n-1])

代码编写

public int deleteAndEarn(int[] nums) { //1. 预处理  int n = 10001; int[] arr = new int[n]; for (int x : nums) arr[x] += x; //2. 创建 dp 表  int[] f = new int[n]; int[] g = new int[n]; //3. 初始化  f[0] = arr[0]; //4. 填表  for (int i = 1; i < n; i++) { f[i] = g[i-1] + arr[i]; g[i] = Math.max(f[i-1], g[i-1]); } return Math.max(f[n-1], g[n-1]); }

• 预处理需要将每个数都映射到数组中去，我们可以先遍历数组，找到最大的那个值，然后开辟一个和最大的数同等规模的数组
  • 但此题 nums 有范围：[1, 10000]
• for-each 循环，x 每出现一次就加在 arr[x] 中

时间复杂度：n+10000
空间复杂度：30000（三张表）

4. 粉刷房子

剑指 Offer II 091. 粉刷房子

算法原理

1. 确定状态表示

   • dp[i][0] 表示：粉刷到 i 位置的时候，最后一个位置粉刷上红色，此时的最小花费
   • dp[i][1] 表示：粉刷到 i 位置的时候，最后一个位置粉刷上蓝色，此时的最小花费
   • dp[i][2] 表示：粉刷到 i 位置的时候，最后一个位置粉刷上绿色，此时的最小花费

2. 状态转移方程

   • dp[i][0] = Math.min (dp[i-1][1], dp[i-1][2]) + costs[i-1][0];
   • dp[i][1] = Math.min (dp[i-1][0], dp[i-1][2]) + costs[i-1][1];
   • dp[i][2] = Math.min (dp[i-1][0], dp[i-1][1]) + costs[i-1][2];

3. 初始化

   • 在最前面加一个虚拟节点，所以原 dp 表整体往后移了一格。之后要找到原始矩阵的值下标就要 -1
   • 虚拟节点的值为 0 即可，0 加上其他值不影响结果

4. 填表顺序

   • 从左往右
   • 三个表一起填

5. 返回值

   • 返回最后一个格子的最小值：Math.min(dp[n][0], Math.min(dp[n][1], dp[n][2]))
   • 因为有一个虚拟节点，所以最后一个格子的下标是 n

代码编写

public int minCost(int[][] costs) { int n = costs.length; int[][] dp = new int[n+1][3]; for (int i = 1; i <= n; i++) { dp[i][0] = Math.min(dp[i-1][1], dp[i-1][2]) + costs[i-1][0]; dp[i][1] = Math.min(dp[i-1][0], dp[i-1][2]) + costs[i-1][1]; dp[i][2] = Math.min(dp[i-1][0], dp[i-1][1]) + costs[i-1][2]; } return Math.min(dp[n][0], Math.min(dp[n][1], dp[n][2])); }