【算法】前缀和
🌈个人主页:秦jh_-CSDN博客
🔥 系列专栏:https://blog.csdn.net/qinjh_/category_12862161.html?fromshare=blogcolumn&sharetype=blogcolumn&sharerId=12862161&sharerefer=PC&sharesource=qinjh_&sharefrom=from_link

目录
【模板】二维前缀和
前言
💬 hello! 各位铁子们大家好哇。
今日更新了前缀和的相关内容
🎉 欢迎大家关注🔍点赞👍收藏⭐️留言📝
【模板】一维前缀和
题目链接:
DP34 【模板】一维前缀和
思路:
前缀和思想,前缀和用来快速求出数组中某一个连续区间的和。
第一步:预处理出来一个前缀和数组。
第二步:使用前缀和数组。
前缀和数组求法:前缀和数组命名为dp,dp[i]表示 [1.i] 区间内所有元素的和。
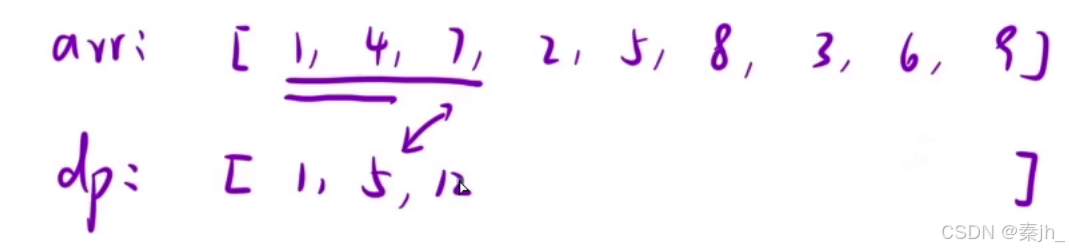
如上图,dp[2]=arr[1]+arr[2] 即1+4=5,不过我们不需要每次都从arr的第一个元素开始加,比如求dp[3],因为已经知道dp[2]了,而dp[2]是arr前两元素的和,所以dp[3]=dp[2]+arr[3]。
也就有一个规律:dp[i]=dp[i-1]+arr[i]
数组下标从1开始,令dp[0]=0,这样就不会影响最终结果,也不用处理特殊情况。因为当下标从0开始的话,dp[i-1]就会出现dp[-1]此时就要处理这种特殊情况了。
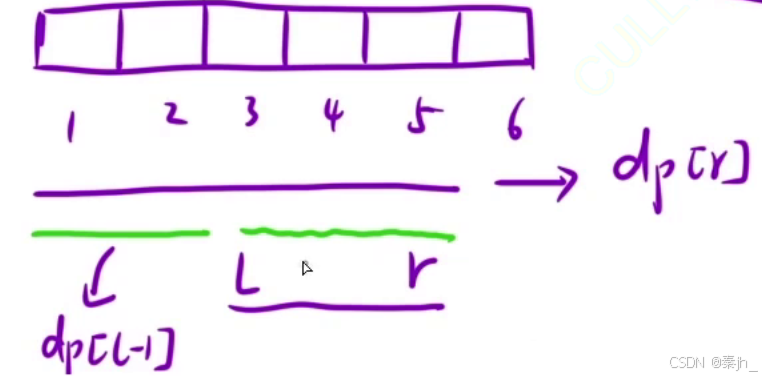
如上图,求数组arr中l~r区间的和时, 只需要用dp[r]-dp[l-1]即可。
【模板】二维前缀和
题目链接:
DP35 【模板】二维前缀和
二维前缀和跟前面的一维前缀和差不多。
思路:
1.预处理出来一个前缀和矩阵。
2.使用前缀和矩阵。
dp[i][j]表示:从[1,1] 位置到 [i,j] 位置,这段区间里面所有元素的和。如下图:
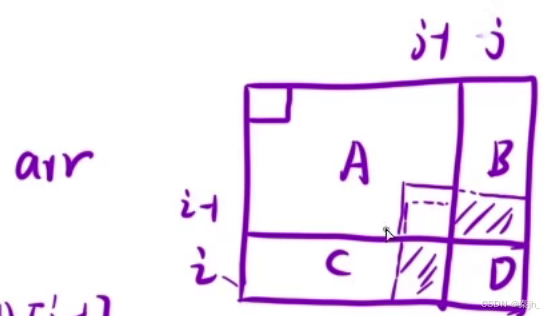
如上图,这是arr数组。如果想求 dp[i][j] ,就等于A区+B区+C区+D元素。B,C区不好求,可以转换成(A+B)+(A+C)+D-A。转换成坐标表示,就可以得到一个规律用来快速求dp[i][j]
即:dp[i][j]=dp[i-1][j]+dp[i][j-1]+arr[i][j]-dp[i-1][j-1]
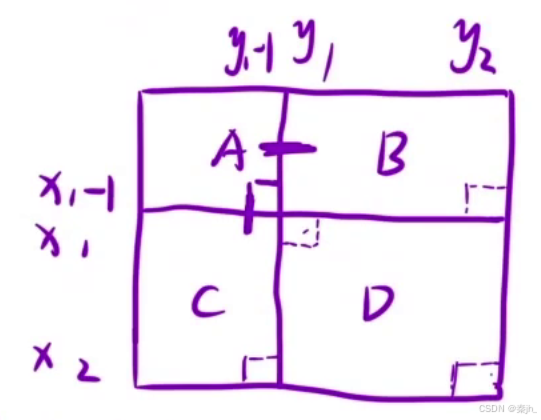
想求[x1,y1]~[x2,y2]区间的和时,可以用整个面积-AB-AC+A来求。
下标表示:D=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]


