网站导航
> 技术文档 > 启发式优化算法——鲸鱼算法_鲸鱼优化算法

启发式优化算法——鲸鱼算法_鲸鱼优化算法

网友: 技术文档 2025-07-30 12:21:01

前言

在我的首篇文章中已介绍了启发式优化算法的相关内容及其在模式识别领域中的应用。本文以使用优化算法优化多机器学习分类器在某二分类模式识别任务时决策级融合（加权投票）的权重为例，介绍鲸鱼算法的原理及实现过程。

1.1 算法原理

鲸鱼算法（Whale Optimization Algorithm, WOA）是一种基于自然界中座头鲸捕食行为的启发式优化算法，由Seyedali Mirjalili和Andrew Lewis于2016年提出。WOA算法模仿了座头鲸独特的泡泡网捕食策略，座头鲸喜欢捕食靠近水面的磷虾群或小鱼。据观察，这种觅食方式是通过沿着圆形或“9”字形路径形成独特的气泡来完成的，如图3-10所示。气泡网捕食是一种独特的行为，只能在座头鲸身上观察到。在这项研究中，螺旋气泡网捕食动作通过数学模型模拟这一过程来解决优化问题。

图1 座头鲸的泡泡网捕食策略示意图

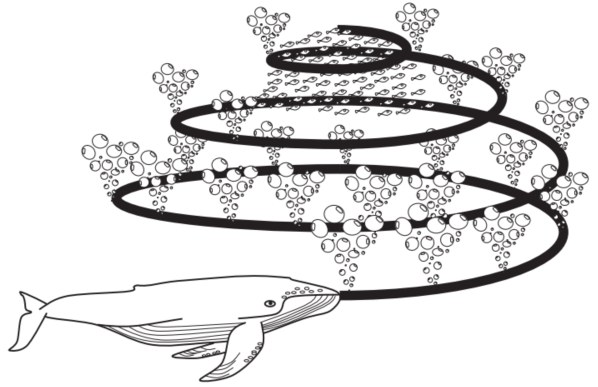
座头鲸泡泡网捕食方法主要分为三个阶段：包围猎物阶段，开发阶段和探索阶段。在包围猎物阶段，进行数学建模的过程是假设当前最佳候选解决方案是目标猎物或接近最优值。在定义最佳搜索代理后，其他搜索代理将尝试更新其位置以靠近最佳搜索代理。此行为可由以下方程表示：

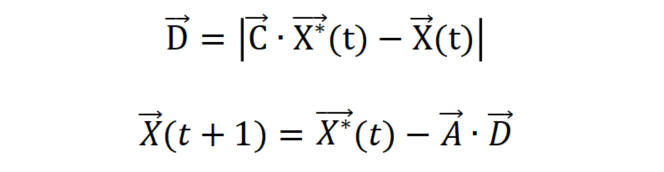
其中t代表当前迭代次数，A和C为系数向量，X^{*}为目前得到最佳解的位置向量，X为当前位置向量，如果有更好的解，则应在每次迭代中更新X^{*} 。

向量\\underset{A}{\\rightarrow}和\\underset{C}{\\rightarrow}的计算过程如下：

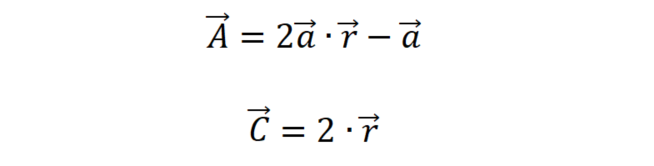
 其中a在迭代过程中从2逐渐减小到0，\\underset{r}{\\rightarrow}是[0, 1]之间的随机值。

在探索猎物阶段，根据座头鲸的习性可分为两种方式：收缩包围机制和螺旋更新位置。收缩包围机制是通过减小式3-7中a值实现的，通过减小a来减小\\underset{A}{\\rightarrow}，从而实现位置的缩小更新。理论上，搜索代理的新位置可以定义在代理的原始位置和当前最佳代理的位置之间的任何位置。

螺旋更新位置机制首先计算位于(X, Y)的鲸鱼与(X^{*},Y^{*})的猎物之间的距离，然后在鲸鱼和猎物之间创建一个螺旋方程，以模仿座头鲸的螺旋运动，如下所示：

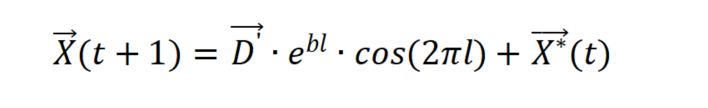
其中， \\underset{\\acute{D}}{\\rightarrow}=\\left | \\underset{X^{*}}{\\rightarrow}(t)-\\underset{X}{\\rightarrow}(t) \\right|表示第i条鲸鱼与猎物的距离（迄今为止获得的最优解），b是定义对数螺旋形状的常数，l是一个[-1, 1]之间的随机数，.代表逐元素乘法。

值得注意的是，座头鲸会同时以收缩环绕机制和螺旋形路径围绕猎物游动。为了模拟这种同时发生的行为，我们假设在优化过程中有50%的概率可以选择收缩环绕机制或螺旋模型来更新鲸鱼的位置。数学模型如下：

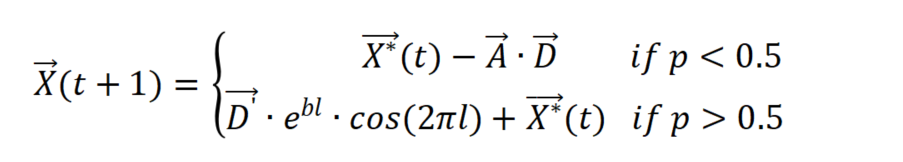
其中p是[0, 1]中的随机数。 

事实上，除了气泡网方法外，座头鲸还会根据彼此的位置随机搜寻猎物。因此，我们使用大于1 或小于−1的随机值的A来迫使搜索代理远离参考鲸鱼。与开发阶段不同，我们在探索阶段根据随机选择的搜索代理而不是迄今为止找到的最佳搜索代理来更新搜索代理的位置。这种机制和 | A| > 1 强调了探索，并允许 WOA 算法执行全局搜索。数学模型如下：

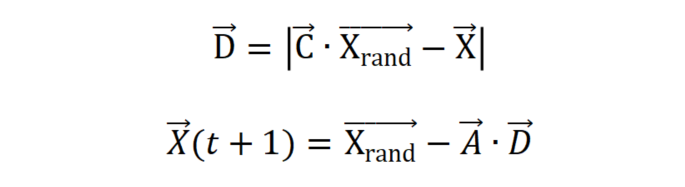
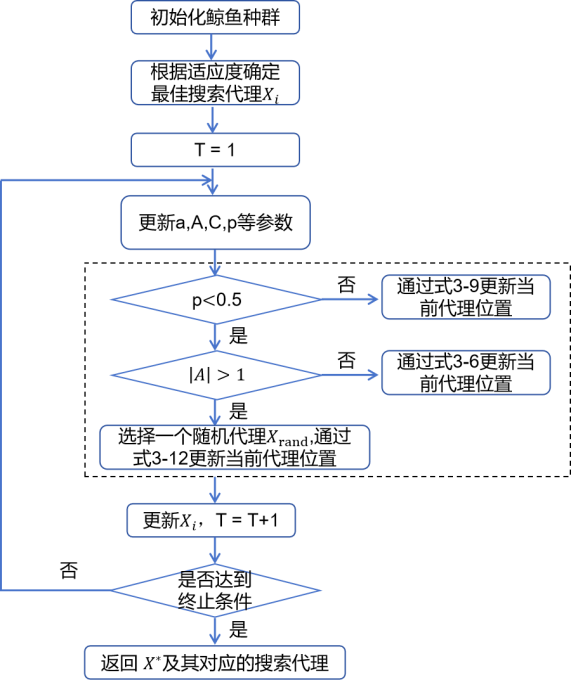
言而总之，WOA算法也是从初始化种群开始，在每次迭代中，搜索代理都会根据随机选择的搜索代理或迄今为止获得的最佳解决方案更新其位置。参数a从2减少到0，以分别提供探索和利用。当 | A| > 1 时，选择随机搜索代理，而当 | A| < 1 时，选择最佳解决方案来更新搜索代理的位置。根据 p 的值，WOA 能够在螺旋或圆形运动之间切换。最后，WOA 算法通过满足终止标准而结束。WOA算法的伪代码如下图所示。 

图2 WOA算法伪代码
图3 WOA算法过程图解

1.2 分类任务示例 

 针对某二分类模式识别任务，本文共采用十种典型的机器学习分类算法。它们分别是：线性判别分析（LDA）、高斯贝叶斯分类器（GNB）、k近邻分类器（KNN）、逻辑回归分类器（LR）、决策树分类器（DT）、随机森林分类器（RF）、支持向量机分类器（SVM）、多层感知机分类器（MLP）、自适应提升分类器（Adaboosting）、梯度提升分类器（GradientBoosting）。以下是分类器的导入方法。

表1 机器学习分类器

机器学习分类器 使用方法 LDA from sklearn.discriminant_analysis import LinearDiscriminantAnalysis GNB     from sklearn.naive_bayes import GaussianNB KNN  from sklearn.neighbors import KNeighborsClassifier LR from sklearn.linear_model import LogisticRegression DT from sklearn import tree RF from sklearn.ensemble import RandomForestClassifier SVM   from sklearn.svm import SVC MLP from sklearn.neural_network import MLPClassifier Adaboosting from sklearn.ensemble import AdaBoostClassifier GradientBoosting  from sklearn.ensemble import GradientBoostingClassifier

 以上分类器均先使用训练集进行训练，训练完毕后使用测试集进行测试，各个分类器在测试集上的准确率如图3所示，其中GBDT分类器的精度最高为93.23%。 

1.3 算法应用

在使用鲸鱼算法对上述十种分类器的投票权重进行优化时，需先初始化鲸鱼种群数量n，在本案例中我们设置n=50，每个个体包含10个维度，取值范围是[0, 1]，即下边界为0，上边界为1，该过程是个随机化的过程，随机在[0, 1]范围内取值。演变截至条件通过最大迭代次数实现，设置iteration=50；接着设置本案例的适应度函数，在本文中将加权投票识别结果的准确率作为适应度函数，如下式所示。

​

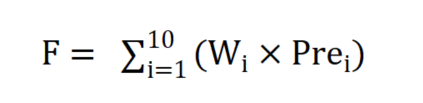
初始条件设置完成后，计算原始种群内每个个体的适应度，从而确定最优适应度X^{*}。按照上述算法流程通过公式3-6至3-12更新，最后在到达停止条件时停止更新并输出最优结果。在本案例中最优解为：

0.00335

0.0192 0.133 0.0192 0.0591 0.0 0.6152 0.2887 0.0314 0.2907

图4展示了使用粒子群算法优化后与未优化之前各个基分类器准确率的对比，从图中不难看出WAO优化后的分类结果为94.13%，比基分类器中最好的GBDT模型提升0.9%。

​
图4十种机器学习分类器与鲸鱼算法优化对比

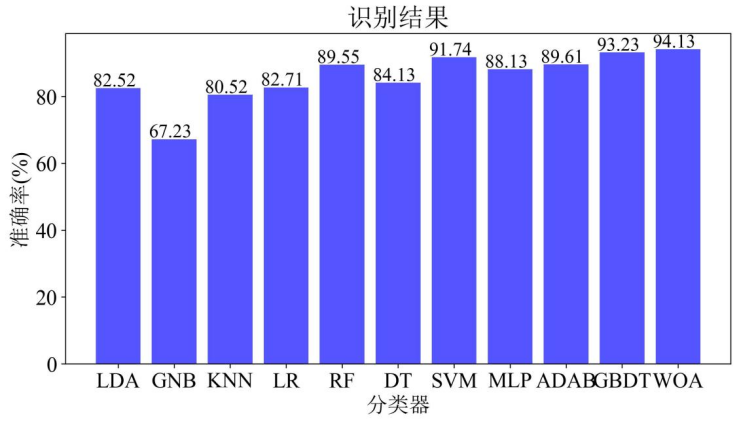
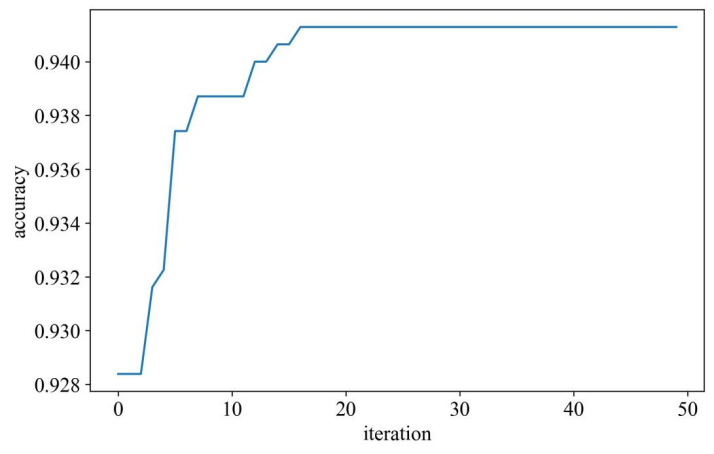
图5展示了算法在优化过程中历代准确率变化趋势。从图中不难看出，鲸鱼算法在该案例的优化过程中收敛速度较快，大概迭代至18次左右收敛至最优解。

​
图3 WOA算法过程图解

这里需要说明的是，鲸鱼算法在python中尚未被封装成高级API，不能通过直接调用相关包来实现优化功能，需要自行编写代码。

1.4 代码演示

导入需要用到的包

 import numpy as npfrom sklearn.metrics import confusion_matrixfrom sklearn.discriminant_analysis import LinearDiscriminantAnalysisfrom sklearn.naive_bayes import GaussianNBfrom sklearn.neighbors import KNeighborsClassifierfrom sklearn.linear_model import LogisticRegressionfrom sklearn.ensemble import RandomForestClassifierfrom sklearn import treefrom sklearn.svm import SVCfrom sklearn.neural_network import MLPClassifierfrom sklearn.ensemble import AdaBoostClassifierimport matplotlib.pyplot as pltplt.rcParams[\'font.family\'] = \'Times New Roman, SimSun\'

定义十种机器学习分类器  

#线性判别分析def lda_classifier(train_x, train_y): model = LinearDiscriminantAnalysis() model.fit(train_x, train_y) return model # 线性回归分类器（贝叶斯分类）def gaussian_classifier(train_x, train_y): model = GaussianNB() model.fit(train_x, train_y) return model # K近邻分类器def knn_classifier(train_x, train_y): model = KNeighborsClassifier() model.fit(train_x, train_y) return model # 逻辑回归分类器def logistic_regression_classifier(train_x, train_y): model = LogisticRegression(penalty=\'l2\',solver=\'lbfgs\', max_iter=100) model.fit(train_x, train_y) return model # 随机森林分类器def random_forest_classifier(train_x, train_y): model = RandomForestClassifier(n_estimators=8,random_state=66) model.fit(train_x, train_y) return model # 决策树分类器def decision_tree_classifier(train_x, train_y): model = tree.DecisionTreeClassifier() model.fit(train_x, train_y) return model # 支持向量机def svm_classifier(train_x, train_y): model = SVC(kernel=\'rbf\', probability=True) model.fit(train_x, train_y) return model # 多层感知机def mlp_classifier(train_x, train_y): model = MLPClassifier(hidden_layer_sizes=(10, 10), max_iter=1000, alpha=0.001, random_state=42) model.fit(train_x, train_y) return model # 自适应提升分类器def ada_boosting_classifier(train_x, train_y): model = AdaBoostClassifier(n_estimators=200) model.fit(train_x, train_y) return model # 梯度提升分类器def gradient_boosting_classifier(train_x, train_y): model = GradientBoostingClassifier(n_estimators=200) model.fit(train_x, train_y) return model # 绘制准确度统计图def plot_acc(acc_list, pso_acc): ary = acc_list ary.append(pso_acc) lab = [\'LDA\',\'GNB\',\'KNN\', \'LR\', \'RF\', \'DT\', \'SVM\', \'MLP\',\'ADAB\',\'GBDT\', \'PSO\'] plt.rcParams.update({\'font.size\': 18}) plt.figure(figsize=(10, 5)) plt.bar(range(len(ary)), ary, color=\'#5555FF\') plt.xticks(range(len(ary)), lab) for j in range(11): plt.text(x=j-0.45, y=ary[j] + 0.6, s=\'%.2f\' % ary[j], fontsize=16) plt.ylabel(\'准确率(%)\', fontsize=18) plt.xlabel(\'分类器\', fontsize=18) plt.title(\'识别结果\') # plt.show() # plt.savefig(\'acc.jpg\',dpi=300, bbox_inches=\'tight\', pad_inches=0.1)

定义鲸鱼算法函数 

# 鲸鱼优化算法class WhaleOptimizationAlgorithm: def __init__(self, pop_size, dim, lb, ub, max_iter, objective_function): self.pop_size = pop_size self.dim = dim self.lb = lb self.ub = ub self.max_iter = max_iter self.fitness_func = objective_function self.Convergence_curve = np.zeros(self.max_iter) # 初始化鲸鱼种群 def initialize_population(self): return np.random.uniform(self.lb, self.ub, (self.pop_size, self.dim)) # 根据p的取值选择对应的捕猎方式(收缩机制/螺旋围捕)，根据A的取值选择鲸鱼是远离还是围绕 def update_position(self, population, A, C, X_star, X, p): if p < 0.5: if abs(A) < 1: new_position = X_star - A * np.abs(C * X_star - X) else: rand_idx = np.random.randint(len(population)) X_rand = population[rand_idx] new_position = X_rand - A * np.abs(C * X_rand - X) else: l = np.random.uniform(-1, 1) new_position = np.abs(X_star - X) * np.exp(l) * np.cos(2 * np.pi * l) + X_star  return new_position # 运行鲸鱼优化算法 def run(self): population = self.initialize_population() fitness = np.array([self.fitness_func(x) for x in population]) X_star = population[np.argmin(fitness)] f_star = np.max(fitness) self.Convergence_curve[0] = f_star a_max = 2 a_min = 0 for t in range(self.max_iter): a = a_max - (a_max - a_min) * (t / self.max_iter) for i in range(self.pop_size): A = 2 * a * np.random.random() - a C = 2 * np.random.random() p = np.random.random() population[i] = self.update_position(population, A, C, X_star, population[i], p) fitness_new = self.fitness_func(population[i]) if fitness_new > f_star:  X_star = population[i]  f_star = fitness_new  self.Convergence_curve[t] = f_star # print(f\"Iteration {t+1}/{self.max_iter}, Best fitness: {f_star}\") return X_star, f_star, self.Convergence_curve

加载分类任务的训练集和测试集完成训练,并输出单分类器的分类指标 

data_train = pd.read_csv(r\"xxx.csv\", header = None)data_test = pd.read_csv(r\"xxx.csv\", header = None)data_train = np.array(data_train)data_test = np.array(data_test) test_classifiers = [\'LDA\',\'GNB\',\'KNN\', \'LR\', \'RF\', \'DT\', \'SVM\', \'MLP\',\'ADAB\',\'GBDT\']classifiers = {\'LDA\':lda_classifier,  \'GNB\':gaussian_classifier, \'KNN\':knn_classifier, \'LR\':logistic_regression_classifier, \'RF\':random_forest_classifier, \'DT\':decision_tree_classifier, \'SVM\':svm_classifier, \'MLP\':mlp_classifier, \'ADAB\':ada_boosting_classifier,  \'GBDT\':gradient_boosting_classifier,  } train_x = data_train[:, :xx]train_y = data_train[:, -1]test_x = data_test[:, :xx]test_y = data_test[:, -1] acc_list = [] for classifier in test_classifiers: model = classifiers[classifier](train_x, train_y) predict = model.predict(test_x) c = confusion_matrix(test_y, predict) acc = (c[0][0] + c[1][1]) / (np.sum(c)) * 100 sens = c[0][0] / np.sum(c[:, 0]) * 100 spec = c[0][0] / np.sum(c[0]) * 100 f1_score = 2*sens*spec/(sens+spec) acc_list.append(acc) print(\'{}分类器的准确率为:{:.2f}%, 精确率为:{:.2f}%, 召回率为:{:.2f}%, F1分数为:{:.2f}%\'.format(classifier, acc, sens, spec, f1_score))
list_model = []for classifier in test_classifiers: model = classifiers[classifier](train_x, train_y) list_model.append(model)print(list_model)

定义适应度函数  

def objective_function(weights): combined_pred = sum(w * p for w, p in zip(weights, predict)) final_pred = np.argmax(combined_pred, axis=1) accuracy = np.mean(final_pred == test_y) return accuracy

初始化算法超参数等

pop_size = 50dim = 10lb = 0ub = 1max_iter = 50predict = [list_model[i].predict_proba(test_x) for i in range(10)]woa = WhaleOptimizationAlgorithm(pop_size, dim, lb, ub, max_iter, objective_function)best_solution, best_fitness, Convergencecurve = woa.run()

可视化训练迭代过程 

plt.figure(figsize=(8, 5))plt.rcParams.update({\'font.size\': 15})plt.plot(Convergencecurve)plt.ylabel(\'accuracy\')plt.xlabel(\'iteration\')# plt.legend()# plt.show()plt.savefig(\'acc_1.jpg\',dpi=300, bbox_inches=\'tight\', pad_inches=0.1)

 打印最优解和最佳适应度

print(\"最优解:\", best_solution)print(\"最优适应度值:\", best_fitness)

 参考文献

MIRJALILI S, LEWIS A. The Whale Optimization Algorithm[J/OL]. Advances in Engineering Software, 2016, 95: 51-67. DOI:10.1016/j.advengsoft.2016.01.008. 

网络标签：

相关问题