C++ Vector算法精讲与底层探秘:从经典例题到性能优化全解析


前引:在C++标准模板库(STL)中,vector作为动态数组的实现,既是算法题解的基石,也是性能优化的关键战场。其连续内存布局、动态扩容机制和丰富的成员函数,使其在面试高频题(如LeetCode、洛谷)中频繁登场。本文聚焦六大经典算法场景(含杨辉三角、去重、结构体排序等),深入解析vector的底层扩容策略、迭代器失效陷阱及内存管理优化技巧,结合代码复现与复杂度对比,帮助开发者从“会用”进阶到“用精”
目录
只出现一次的数字I
原理讲解
代码展示
杨辉三角
原理讲解
代码展示
电话号码字母组合
原理讲解
代码展示
整型去重
原理讲解
代码展示
找只出现一次的数字II
原理讲解
代码展示
只出现一次的数字III
编辑原理讲解
代码展示
编辑
只出现一次的数字I
https://leetcode.cn/problems/single-number 
原理讲解
这种题可以通过排序来找,但最高效的是按位异或:^
按位异或原理:比较二进制,相同为0,相异为1,如果两个数字一模一样去异或,那么就可以消除
代码展示
class Solution {public: int singleNumber(vector& nums) { int tmp=0; for(int i=0;i<nums.size();i++) { tmp^=nums[i]; } return tmp; }};当然用范围for、迭代器也是可以的,因为也是遍历(支持迭代器就支持范围for)
class Solution {public: int singleNumber(vector& nums) { int tmp=0; //范围for for(auto e:nums) { tmp^=e; } return tmp; }};class Solution {public: int singleNumber(vector& nums) { int tmp=0; //迭代器 auto it = nums.begin(); while(it!=nums.end()) { tmp ^= (*it); it++; } return tmp; }};杨辉三角
原理讲解
(1)第一步
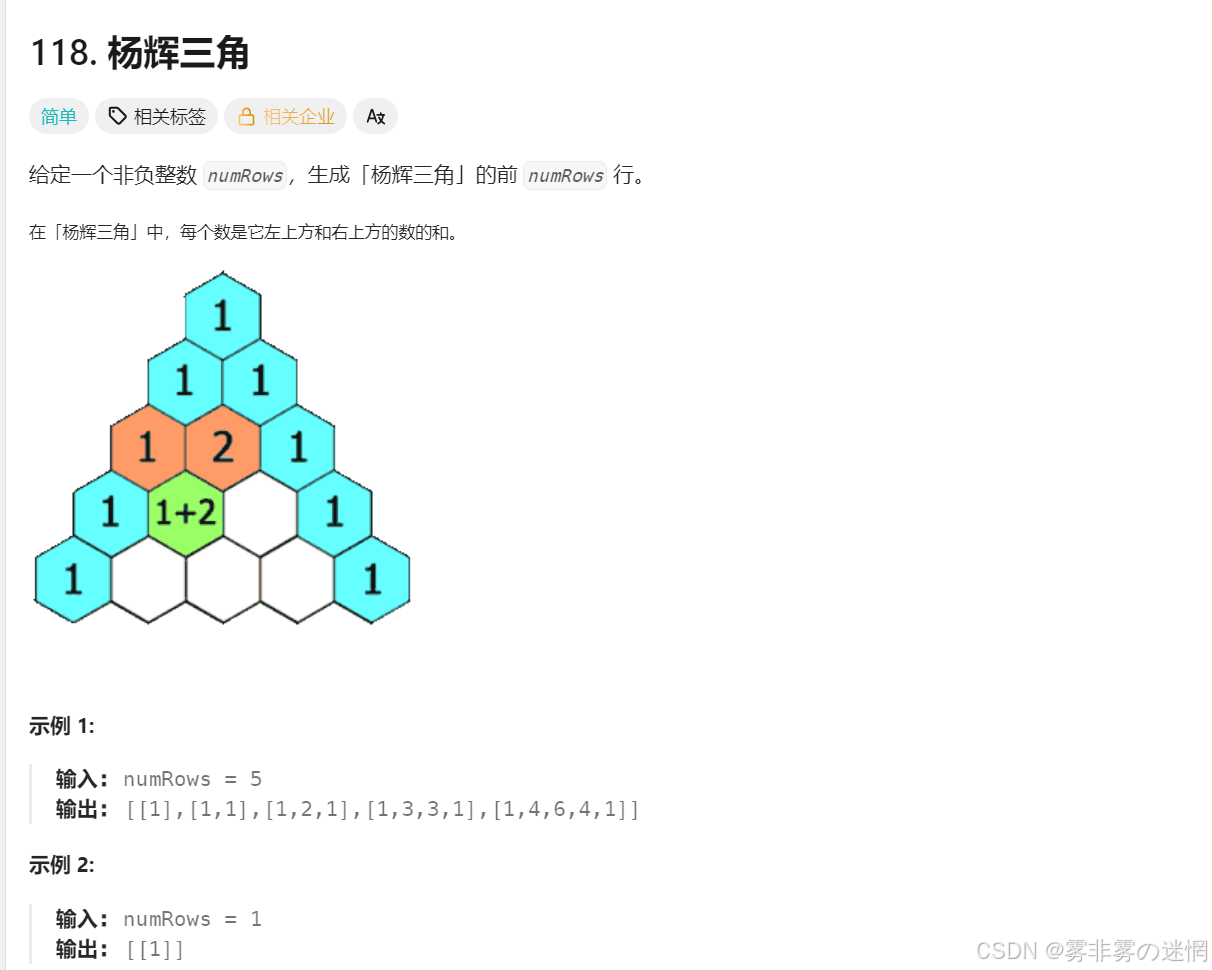
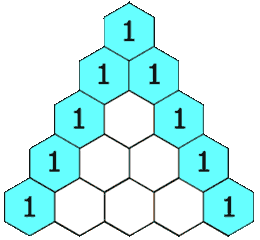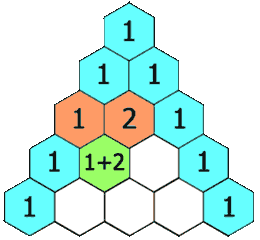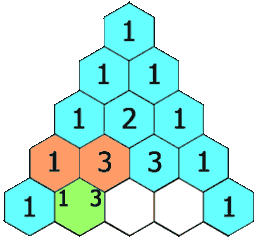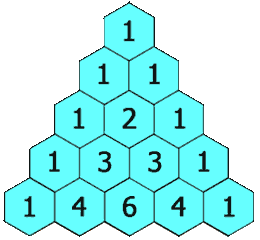
首先两数的计算肯定是没有问题的,对应两个数相加即可,下面我来此题转化一下得到它的本质

从上图看见这是一个二维数组,每行的元素个数都不同,我们可以采用vector来开辟一个二维数组,下面我们来看如何开辟:vector<vector>vector这是二维数组类型,为何 int 不用 int*?
外面的vector表示开辟了一定数量的类型元素,比如:vector<vector> 5,表示5个vector

而里面的每个vector又是一个类型,这样我们可以先访问外面的->里面的,达到二维数组

如果用vector<vector*>表示一定数量的一级指针也是可以的,只是访问方式就需要解引用了
(2)第二步,初始化
我们可以先通过下标访问里面的vector,再调用resize给对应的vector开辟空间+初始化
(3)计算对应的位置
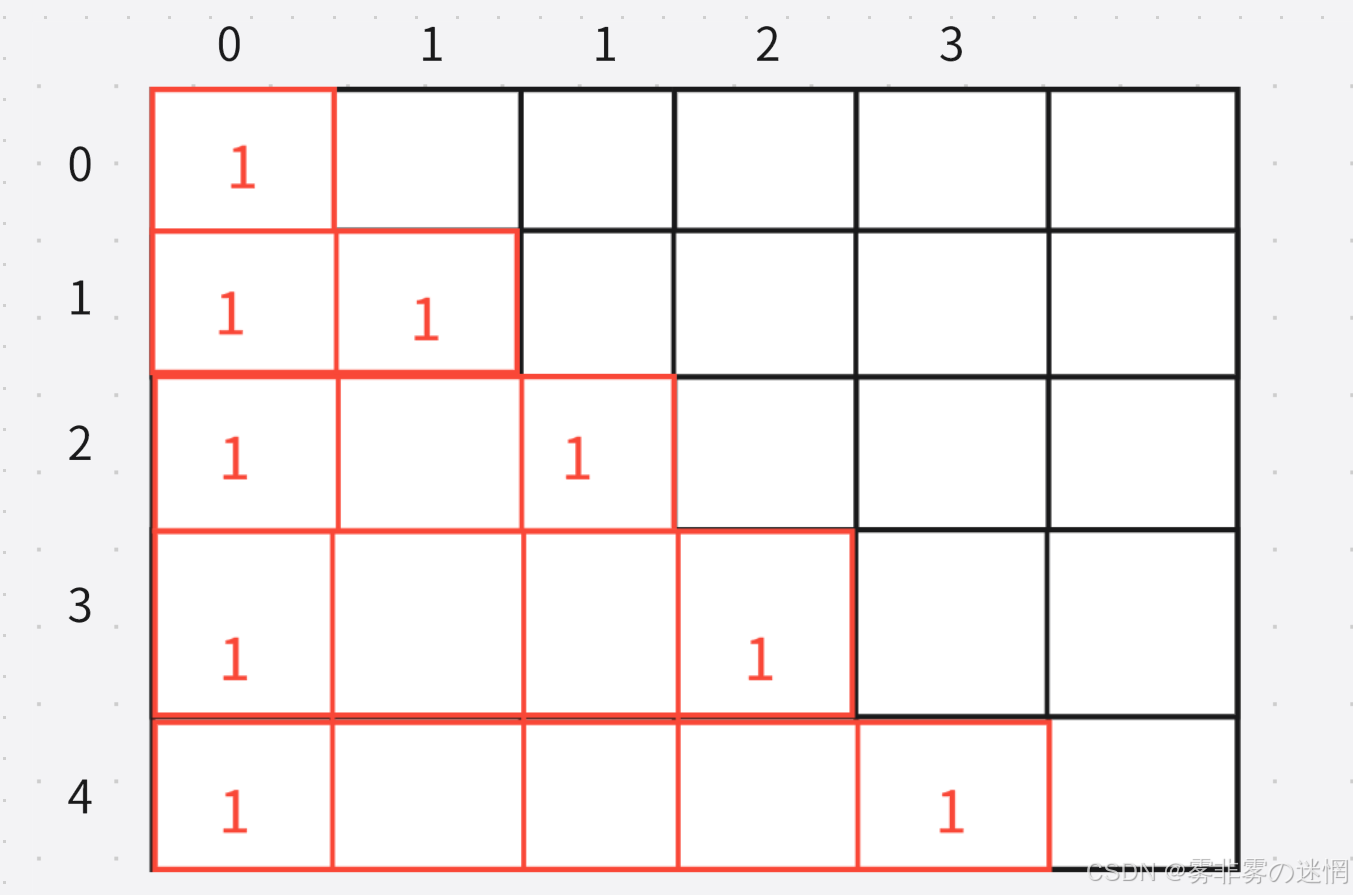
可以看到左边是从下标2开始,右边是从下标1开始,那么空格的元素为【i-1,j-1】+【i-1,j】之和
代码展示
class Solution {public: vector<vector> generate(int numRows) { //开辟行数 vector<vector> V(numRows); //开辟二维数组(开辟+初始化) for(int i=0;i<numRows;i++) { V[i].resize(i+1,1); } //计算指定元素 for(int i=2;i<numRows;i++) { for(int j=1;j<i;j++) { V[i][j]=V[i-1][j]+V[i-1][j-1]; } } return V; }};电话号码字母组合
https://leetcode.cn/problems/letter-combinations-of-a-phone-number

题目解读:
我们可以看到每个数字都代表着一串字符,题目会给你一串字符数字,让你用这些数字所映射的字符串去根据里面的字符组合出不同的字符串,例如:给你“34”。3代表“def”,4代表“ghi”,它们可以组合出:“dg”、“dh”、“di”、“eg”、“eh”、“ei”、“fg”、“fh”、“fi”,将这些字符串放在vector里面,返回即可
原理讲解
这题需要用到多参的递归,下面小编一步步讲解
(1)首先我们需要表达映射关系,比如“2”对应“abc”,“3对应“def”,以此类推
//映射关系string str[10]={\"\",\"\",\"abc\",\"def\",\"ghi\",\"jkl\",\"mno\",\"pqs\",\"tuv\",\"wxyz\"};(2)递归函数参数:题目给的数字组合、数字下标、组合的字符串、vector存储

class Solution { //映射关系 string str[10]={\"\",\"\",\"abc\",\"def\",\"ghi\",\"jkl\",\"mno\",\"pqs\",\"tuv\",\"wxyz\"};public: //递归函数 void Compare(string digits,int val,string news,vector&) { //函数实现 } vector letterCombinations(string digits) { vector V; //如果是空串,直接返回 if(digits.empty()) { return V; } //调用递归函数 Compare(digits,0,\"\",V); //返回结果 return V; }};参数的解释:digits方便我们找到数字字母、val为数字下标、news是组合得到的字符串
(2)首先要拿到第一位数字字母映射的内容,由数字下标找到数字映射的字符串
/拿到映射内容int tmp=digits[val]-\'0\';string stl_=str[tmp];(3)此时我们可以通过循环控制当前的字符:def,例如:
//从第一个字母开始组合for(int i=0;i<stl_size();i++){ //进入第二层for循环}
此时 i 为0,也就是指向d,下面我们想组合出 dg、dh、di,还需要调用递归函数
(4)函数的参数:
Compare(digits,val+1,news+stll[i],V);ghi 是第二个数字映射的字符串,但是又不能真正改变val,因为后面要回溯
此时相当于news从原来的 \"\" 变成了 \"d\",也不能真正改变news,因为后面要回溯否则就累积了
(5)现在是递归的结束条件,如果组合完每层的字母,那就返回,回到第一层for循环,重新开始
//递归结束条件if(val==digits.size()){ //存储 V.push_back(news); return;}梳理递归思路:

代码展示
class Solution { //映射关系 string str[10]={\"\",\"\",\"abc\",\"def\",\"ghi\",\"jkl\",\"mno\",\"pqrs\",\"tuv\",\"wxyz\"};public: //递归函数 void Compare(string digits,int val,string news,vector& V) { //递归结束条件 if(val==digits.size()) { //存储 V.push_back(news); return; } //拿到映射内容 int tmp=digits[val]-\'0\'; string stll=str[tmp]; //从第一个字母开始组合 for(int i=0;i<stll.size();++i) { //进入第二层for循环 Compare(digits,val+1,news+stll[i],V); } } vector letterCombinations(string digits) { vector V; if(digits.empty()) { return V; } //调用递归函数 Compare(digits,0,\"\",V); //返回结果 return V; }};整型去重
https://leetcode.cn/problems/remove-duplicates-from-sorted-array

原理讲解
(1)首先我们不管此类去重题有没有序,如果没有,调用Sort函数先排序
(2) 如果本身已经有序,使用:unique+erase 去重组合即可(适用任何类型)
unique 接口作用:
返回一个迭代器,指向去重后序列的末尾(即最后一个不重复元素的下一个位置)
unique 接口参数:
序列范围:begin(),end()
erase 接口作用:
指定删除范围内的元素,并将之后的元素前移
注意:unique 的范围必须有序,且必须保存返回值作为erase的输入范围点
erase之后迭代器会失效,如果需要重复使用,需要接收erase的返回值
例如:

代码展示
class Solution {public: int removeDuplicates(vector& nums) { auto new_end=unique(nums.begin(),nums.end()); nums.erase(new_end,nums.end()); return nums.size(); }};找只出现一次的数字II
https://leetcode.cn/problems/single-number-iii

原理讲解
(1)先算出不同的两个整型的异或结果(比如:1、2、1、3、2、5,异或和结果为6)
(2)找到找到最低位的1(注意整型溢出)
int mask = (tmp == INT_MIN ? tmp : tmp & (-tmp));
(3)将最低位为1的进行分组,最后得到只出现一次的两个数字

代码展示
class Solution {public: vector singleNumber(vector& nums) { //计算异或和 int tmp = 0; for (auto e : nums) { tmp ^= e; } //算最低位的1 int mask = (tmp == INT_MIN ? tmp : tmp & (-tmp)); //分组异或 int a = 0; int b = 0; for (auto e : nums) { if (e & mask) { a ^= e; } else { b ^= e; } } return {a, b}; }};只出现一次的数字III
https://leetcode.cn/problems/single-number-iii
 原理讲解
原理讲解
出现3次的数字它的该为加起来至少是3,例如:

代码展示
class Solution {public: int singleNumber(vector& nums) { int ans = 0; //遍历二进制的每一位 for (int i = 0; i > i) & 1); } //模3去重 if (total % 3) { ans |= (1 << i); } } return ans; }};【雾非雾】期待与你的下次相遇!



