网站导航
> 技术文档 > 【算法解析5/5 下】强化学习（RL）深度解析：常用主流算法（附Python代码）|动态规划、蒙特卡洛方法、时序差分学习、Q-Learning、策略梯度与Actor-Critic方法|优缺点与工程建议_rl 有哪些常见算法

【算法解析5/5 下】强化学习（RL）深度解析：常用主流算法（附Python代码）|动态规划、蒙特卡洛方法、时序差分学习、Q-Learning、策略梯度与Actor-Critic方法|优缺点与工程建议_rl 有哪些常见算法

网友: 技术文档 2025-07-30 12:27:44

注：本系列将有五部分，分别对应五大机器学习任务类型，包括：
1. 分类（Classification）、2. 回归（Regression）、3. 聚类（Clustering）、4. 降维（Dimensionality Reduction）以及 5. 强化学习（Reinforcement Learning）
此文含大量干货，建议收藏方便以后再读！

注：此为两部分中的下部，上部请按下面链接前往！（强烈建议先看上部分）

【算法解析5/5 上】强化学习（RL）深度解析：常用算法、数学目标与核心公式、与其他任务的差别 | 状态、动作、奖励、策略、环境转移概率、折扣因子 | MDP、累积奖励、策略与价值函数、贝尔曼方程-CSDN博客

大家好，我是爱酱。强化学习是机器学习五大任务中最具挑战性和潜力的分支之一，广泛应用于智能控制、博弈、机器人、自动驾驶、推荐系统等地方。作为强化学习专题的第二部分，本节将围绕实际案例，详细讲解强化学习的典型算法、核心思想、数学表达与操作流程，帮助你系统掌握强化学习的实践方法。（将继续延续上部分的完结部分）

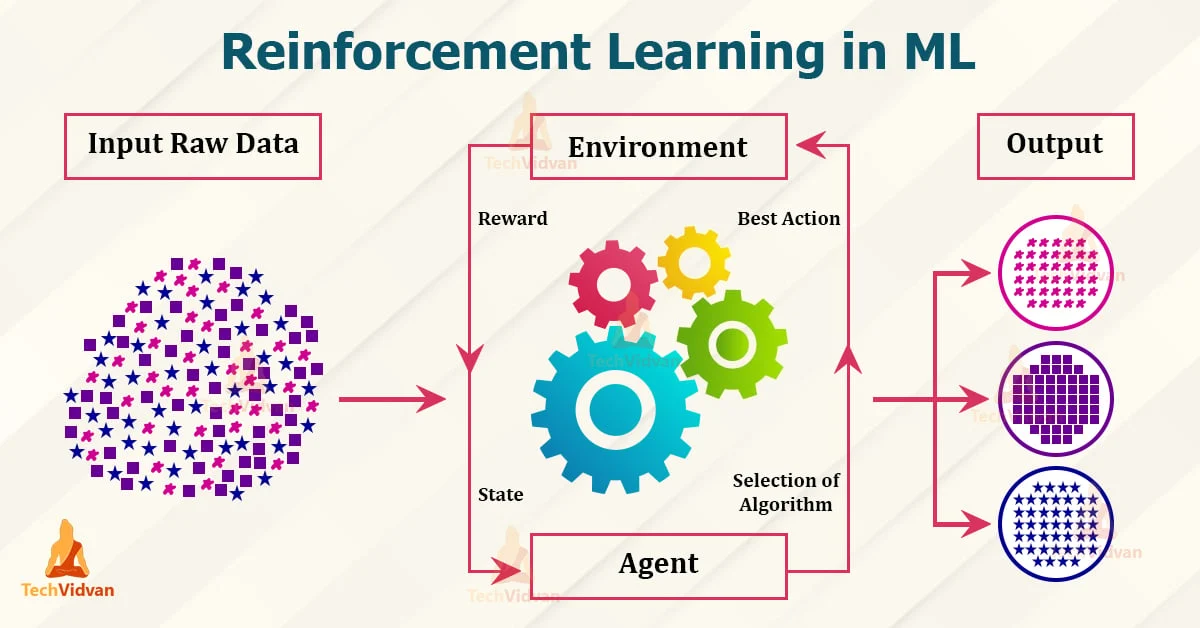
七、强化学习主流算法与详细流程

1. 动态规划（Dynamic Programming, DP）

适用场景：环境模型已知（即状态转移概率$P$和奖励$R$已知）
代表方法：值迭代（Value Iteration）、策略迭代（Policy Iteration）

值迭代核心流程

  • 初始化所有状态的价值$V(s)$为0

  • 重复更新：对每个状态$s$，按贝尔曼方程迭代

    V_{k+1}(s) = \\max_{a} \\sum_{s\'} P(s\'|s,a) [R(s,a,s\') + \\gamma V_k(s\')]

  • 直到$V(s)$收敛，提取最优策略$\\pi^*(s) = \\arg\\max_a \\sum_{s\'} P(s\'|s,a)[R(s,a,s\') + \\gamma V(s\')]$

优缺点：理论完备，但需环境模型，难以扩展到大规模或未知环境。

2. 蒙特卡洛方法（Monte Carlo Methods）

适用场景：环境模型未知，但能采样完整回合
核心思想：通过多次采样完整轨迹，直接用经验平均累计奖励估计价值函数

流程

  • 反复采样完整回合，记录每步状态、动作、奖励

  • 每个状态的价值由其后续实际累计奖励的平均值估计

  • 可用于策略评估和策略改进

优缺点：无需环境模型，样本利用率低，需完整回合。

3. 时序差分学习（Temporal Difference, TD）

适用场景：环境模型未知，可在线学习
核心思想：结合动态规划和蒙特卡洛，边采样边更新价值函数

TD(0)更新公式

V(s_t) \\leftarrow V(s_t) + \\alpha [r_t + \\gamma V(s_{t+1}) - V(s_t)]

  • 每一步采样后立即更新当前状态的价值估计

  • TD($\\lambda$)可结合多步信息，提升效率

优缺点：无需完整回合，学习速度快，理论基础扎实。

4. Q-Learning（离线/无模型强化学习）

适用场景：环境模型未知，目标学得最优策略
核心思想：直接学习最优动作价值函数$Q^*(s,a)$，不依赖环境模型

Q-Learning更新公式

Q(s_t, a_t) \\leftarrow Q(s_t, a_t) + \\alpha [r_t + \\gamma \\max_{a\'} Q(s_{t+1}, a\') - Q(s_t, a_t)]

  • 训练目标是学会最优策略$\\pi^(s) = \\arg\\max_a Q^(s,a)$

  • 采用$\\epsilon$-贪婪策略平衡探索与利用

优缺点：简单高效，理论保证收敛，适合离线学习和大规模问题。

5. 策略梯度与Actor-Critic方法

适用场景：动作空间大或连续、策略需直接优化
核心思想：直接优化参数化策略$\\pi_\\theta(a|s)$，通过采样估计梯度并更新参数

策略梯度公式

\\nabla_\\theta J(\\theta) = \\mathbb{E}_\\pi [\\nabla_\\theta \\log \\pi_\\theta(a|s) Q^\\pi(s,a)]

  • Actor-Critic结合了价值函数和策略优化，提升训练效率和稳定性

  • 适合复杂、高维、连续动作空间

优缺点：适用范围广，收敛速度快，但易陷入局部最优，对超参数敏感。

八、（简单版）强化学习案例流程与代码演示

案例：迷宫寻路（GridWorld）Q-Learning

1. 环境描述

  • $5\\times5$迷宫，智能体起点$(0,0)$，目标点$(4,4)$，每步奖励$-1$，到达目标奖励$+10$

  • 动作：上、下、左、右

2. Q-Learning详细流程

  1. 初始化$Q(s,a)$为0

  2. 对每一回合：

    • 智能体从起点出发

    • 按$\\epsilon$-贪婪策略选择动作

    • 执行动作，获得新状态和奖励

    • 按Q-Learning公式更新$Q(s,a)$

    • 到达目标或步数耗尽则回合结束

  3. 重复多回合，Q值逐渐收敛，智能体学会最短路径

3. Python代码示例（简易版）

import numpy as npimport matplotlib.pyplot as plt# 1. 环境参数n_states = 5 # 5x5网格actions = [\'up\', \'down\', \'left\', \'right\']action_dict = {0: (-1, 0), 1: (1, 0), 2: (0, -1), 3: (0, 1)}goal_state = (4, 4)# 2. Q表初始化Q = np.zeros((n_states, n_states, len(actions)))# 3. Q-Learning参数alpha = 0.1 # 学习率gamma = 0.9 # 折扣因子epsilon = 0.2 # 探索率episodes = 500 # 训练回合数max_steps = 100 # 每回合最大步数# 4. 环境step函数def step(state, action): x, y = state dx, dy = action_dict[action] nx, ny = x + dx, y + dy # 边界处理 nx = min(max(nx, 0), n_states - 1) ny = min(max(ny, 0), n_states - 1) next_state = (nx, ny) # 奖励设计 if next_state == goal_state: reward = 10 done = True else: reward = -1 done = False return next_state, reward, done# 5. Q-Learning主循环for episode in range(episodes): state = (0, 0) for step_count in range(max_steps): # epsilon-贪婪策略 if np.random.rand() < epsilon: action = np.random.choice(len(actions)) else: action = np.argmax(Q[state[0], state[1]]) next_state, reward, done = step(state, action) # Q值更新 Q[state[0], state[1], action] += alpha * ( reward + gamma * np.max(Q[next_state[0], next_state[1]]) - Q[state[0], state[1], action] ) state = next_state if done: breakprint(\"Q-Learning训练完成！\")# 6. 策略展示（从起点到终点的最优路径）def get_optimal_path(Q, start, goal): path = [start] state = start for _ in range(100): action = np.argmax(Q[state[0], state[1]]) next_state, _, _ = step(state, action) path.append(next_state) if next_state == goal: break state = next_state return pathoptimal_path = get_optimal_path(Q, (0,0), goal_state)print(\"最优路径:\", optimal_path)# 7. 可视化最优路径grid = np.zeros((n_states, n_states))for (x, y) in optimal_path: grid[x, y] = 1grid[goal_state] = 2plt.figure(figsize=(6,6))plt.imshow(grid, cmap=\'Blues\', origin=\'upper\')plt.title(\'Optimal Path in GridWorld\')plt.xticks(range(n_states))plt.yticks(range(n_states))plt.xlabel(\'Y\')plt.ylabel(\'X\')for (x, y) in optimal_path: plt.text(y, x, \'●\', ha=\'center\', va=\'center\', color=\'red\', fontsize=16)plt.text(goal_state[1], goal_state[0], \'G\', ha=\'center\', va=\'center\', color=\'green\', fontsize=16)plt.gca().invert_yaxis()plt.show()

代码说明

  • step函数：定义了智能体在网格环境中的移动和奖励规则。

  • Q-Learning主循环：每回合从起点出发，采用$\\epsilon$-贪婪策略探索，更新Q表。

  • get_optimal_path：利用训练好的Q表，从起点出发，按最优策略走到终点，记录路径。

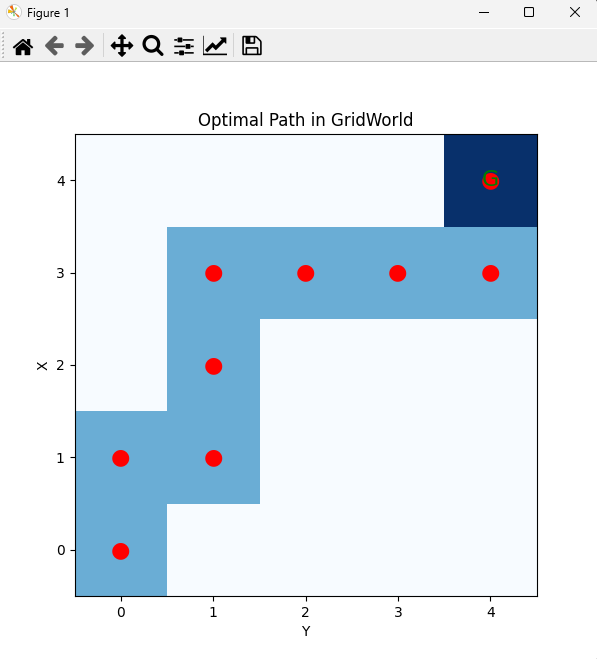
  • 可视化：用matplotlib画出最优路径，终点用绿色G标记，路径用红色圆点标记。

 九、（复杂版）强化学习案例流程与代码演示（GridWorld + 障碍物 + pygame 可视化）

1. 环境设定

  • 5x5 网格世界，智能体起点 (0,0)，终点 (4,4)

  • 有若干障碍物（如(1,2)、(2,2)、(3,1)），智能体不能走进障碍格

  • 每步奖励 -1，走进终点奖励 +10，碰到障碍物奖励 -5（并停在原地）

  • 四个动作：上、下、左、右

2. Q-Learning 流程

  1. 初始化 Q 表为 0

  2. 每回合从起点出发，最多走 max_steps 步

  3. 按 $\\epsilon$-贪婪策略选择动作

  4. 执行动作，获得新状态和奖励

    • 若撞到障碍物，奖励 -5，停在原地

    • 若到终点，奖励 +10，回合结束

    • 否则奖励 -1

  5. 按 Q-Learning 公式更新 Q 表

  6. 多回合训练后，Q 表收敛，智能体学会避开障碍、走最短路

3. Python代码实现（含pygame可视化）

1）安装依赖（Dependency）
pip install pygame numpy
2）完整代码
import numpy as npimport pygameimport sysimport time# 环境参数n_states = 5actions = [\'up\', \'down\', \'left\', \'right\']action_dict = {0: (-1, 0), 1: (1, 0), 2: (0, -1), 3: (0, 1)}goal_state = (4, 4)obstacles = [(1,2), (2,2), (3,1)]# Q表初始化Q = np.zeros((n_states, n_states, len(actions)))# Q-Learning参数alpha = 0.1gamma = 0.9epsilon = 0.2episodes = 1000max_steps = 50def step(state, action): x, y = state dx, dy = action_dict[action] nx, ny = x + dx, y + dy # 边界处理 nx = min(max(nx, 0), n_states - 1) ny = min(max(ny, 0), n_states - 1) next_state = (nx, ny) if next_state in obstacles: reward = -5 next_state = state # 碰到障碍物停在原地 done = False elif next_state == goal_state: reward = 10 done = True else: reward = -1 done = False return next_state, reward, done# Q-Learning主循环for episode in range(episodes): state = (0, 0) for step_count in range(max_steps): if np.random.rand()  0: prev = path[idx-1] start = (prev[1]*CELL_SIZE + CELL_SIZE//2, prev[0]*CELL_SIZE + CELL_SIZE//2) pygame.draw.line(screen, (255,0,0), start, center, 3) pygame.display.flip()# 展示最优路径动画for i in range(1, len(optimal_path)+1): draw_grid(optimal_path[:i]) for event in pygame.event.get(): if event.type == pygame.QUIT: pygame.quit() sys.exit() time.sleep(0.5)# 等待关闭while True: for event in pygame.event.get(): if event.type == pygame.QUIT: pygame.quit() sys.exit()

代码说明

  • 环境定义：障碍物用黑色格子，起点蓝色，终点绿色。

  • Q-Learning训练：遇到障碍物会被惩罚并停在原地，终点奖励高。

  • 路径获取：智能体按最优策略走到终点，自动避开障碍。

  • pygame动画：动态展示最优路径，红色圆点和线段显示智能体移动轨迹。

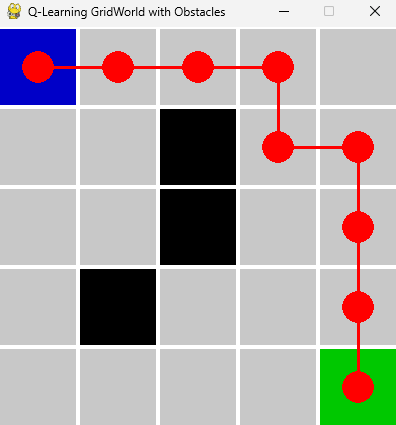
你可以直接运行这段代码，看到智能体如何学会避开障碍、走最优路径，并用pygame动态展示全过程。如果需要更大地图、更多障碍、不同奖励设计或更酷的可视化。

十、强化学习的优缺点与工程建议

优点：

  • 能解决无标签、反馈稀疏、动态决策等复杂问题

  • 适应性强，可自主探索最优策略

  • 理论基础扎实，适合长期收益优化场景

缺点：

  • 训练效率低，样本利用率不高

  • 对环境建模、奖励设计敏感

  • 训练过程可能不稳定，调参复杂

工程建议：

  • 环境建模和奖励函数设计需贴合实际目标

  • 结合模拟、并行采样等手段提升训练效率

  • 可用深度学习（DQN、PPO等）扩展到高维感知任务

十一、总结

强化学习通过智能体与环境的交互、试错和奖励反馈，最终学会最优策略，是解决序列决策和长期收益优化问题的强大工具。理解MDP、贝尔曼方程、Q-Learning、策略梯度等核心理论与算法，有助于你在智能控制、自动决策等前沿场景中发挥强化学习的威力。

注：还没看上部分的伙伴记得先回去看看喔～会对理解这部分有帮助喔！

谢谢你看到这里，你们的每个赞、收藏跟转发都是我继续分享的动力。

如需进一步案例、代码实现或与其他聚类算法对比，欢迎留言交流！我是爱酱，我们下次再见，谢谢收看！

网络标签：

相关问题