【深度学习优化算法】09：Adadelta算法

【作者主页】Francek Chen
【专栏介绍】$\lceil$PyTorch深度学习$\rfloor$ 深度学习 (DL, Deep Learning) 特指基于深层神经网络模型和方法的机器学习。它是在统计机器学习、人工神经网络等算法模型基础上，结合当代大数据和大算力的发展而发展出来的。深度学习最重要的技术特征是具有自动提取特征的能力。神经网络算法、算力和数据是开展深度学习的三要素。深度学习在计算机视觉、自然语言处理、多模态数据分析、科学探索等地方都取得了很多成果。本专栏介绍基于PyTorch的深度学习算法实现。
【GitCode】专栏资源保存在我的GitCode仓库：https://gitcode.com/Morse_Chen/PyTorch_deep_learning。

文章目录

• • 一、算法
  • 二、代码实现
  • 小结

  Adadelta是AdaGrad的另一种变体，主要区别在于前者减少了学习率适应坐标的数量。此外，广义上Adadelta被称为没有学习率，因为它使用变化量本身作为未来变化的校准。

一、算法

  简而言之，Adadelta使用两个状态变量， s t \\mathbf{s}_t st​用于存储梯度二阶导数的泄露平均值， Δ x t \\Delta\\mathbf{x}_t Δxt​用于存储模型本身中参数变化二阶导数的泄露平均值。请注意，为了与其他出版物和实现的兼容性，我们使用作者的原始符号和命名（没有其它真正理由让大家使用不同的希腊变量来表示在动量法、AdaGrad、RMSProp和Adadelta中用于相同用途的参数）。

  以下是Adadelta的技术细节。鉴于参数du jour是$\rho$，我们获得了与RMSProp算法类似的以下泄漏更新：
s t = ρ s t − 1 + ( 1 − ρ ) g t 2 (1) \\begin{aligned} \\mathbf{s}_t & = \\rho \\mathbf{s}_{t-1} + (1 - \\rho) \\mathbf{g}_t^2 \\end{aligned} \\tag{1} st​​=ρst−1​+(1−ρ)gt2​​(1) 与RMSProp算法的区别在于，我们使用重新缩放的梯度 g t ′ \\mathbf{g}_t\' gt′​执行更新，即
x t = x t − 1 − g t ′ (2) \\begin{aligned} \\mathbf{x}_t & = \\mathbf{x}_{t-1} - \\mathbf{g}_t\' \\end{aligned}\\tag{2} xt​​=xt−1​−gt′​​(2) 那么，调整后的梯度 g t ′ \\mathbf{g}_t\' gt′​是什么？我们可以按如下方式计算它：
g t ′ = Δ x t − 1 + ϵ s t + ϵ ⊙ g t (3) \\begin{aligned} \\mathbf{g}_t\' & = \\frac{\\sqrt{\\Delta\\mathbf{x}_{t-1} + \\epsilon}}{\\sqrt{{\\mathbf{s}_t + \\epsilon}}} \\odot \\mathbf{g}_t \\\\ \\end{aligned} \\tag{3} gt′​​=st​+ϵ ​Δxt−1​+ϵ ​​⊙gt​​(3) 其中 Δ x t − 1 \\Delta \\mathbf{x}_{t-1} Δxt−1​是重新缩放梯度的平方 g t ′ \\mathbf{g}_t\' gt′​的泄漏平均值。我们将 Δ x 0 \\Delta \\mathbf{x}_{0} Δx0​初始化为$0$，然后在每个步骤中使用 g t ′ \\mathbf{g}_t\' gt′​更新它，即
Δ x t = ρ Δ x t − 1 + ( 1 − ρ ) g t ′2 (4) \\begin{aligned} \\Delta \\mathbf{x}_t & = \\rho \\Delta\\mathbf{x}_{t-1} + (1 - \\rho) {\\mathbf{g}_t\'}^2 \\end{aligned} \\tag{4} Δxt​​=ρΔxt−1​+(1−ρ)gt′​2​(4)

  $ϵ$（例如 1 0 − 5 10^{-5} 10−5这样的小值）是为了保持数字稳定性而加入的。

二、代码实现

  Adadelta需要为每个变量维护两个状态变量，即 s t \\mathbf{s}_t st​和 Δ x t \\Delta\\mathbf{x}_t Δxt​。这将产生以下实现。

%matplotlib inlineimport torchfrom d2l import torch as d2ldef init_adadelta_states(feature_dim): s_w, s_b = torch.zeros((feature_dim, 1)), torch.zeros(1) delta_w, delta_b = torch.zeros((feature_dim, 1)), torch.zeros(1) return ((s_w, delta_w), (s_b, delta_b))def adadelta(params, states, hyperparams): rho, eps = hyperparams[\'rho\'], 1e-5 for p, (s, delta) in zip(params, states): with torch.no_grad(): # In-placeupdatesvia[:] s[:] = rho * s + (1 - rho) * torch.square(p.grad) g = (torch.sqrt(delta + eps) / torch.sqrt(s + eps)) * p.grad p[:] -= g delta[:] = rho * delta + (1 - rho) * g * g p.grad.data.zero_()

  对于每次参数更新，选择$\rho =0.9$相当于10个半衰期。由此我们得到：

data_iter, feature_dim = d2l.get_data_ch11(batch_size=10)d2l.train_ch11(adadelta, init_adadelta_states(feature_dim), {\'rho\': 0.9}, data_iter, feature_dim);

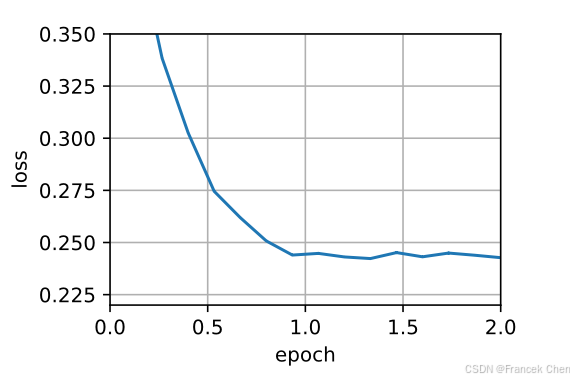
  为了简洁实现，我们只需使用高级API中的Adadelta算法。

trainer = torch.optim.Adadeltad2l.train_concise_ch11(trainer, {\'rho\': 0.9}, data_iter)

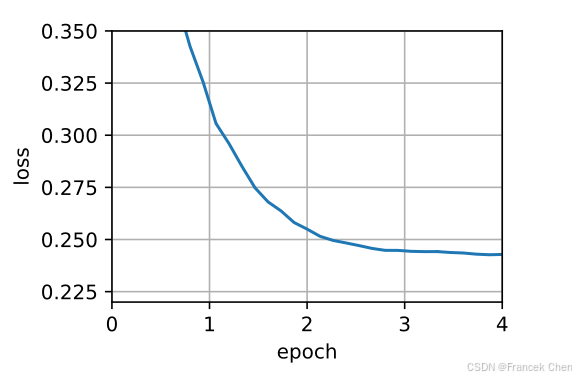
小结

• Adadelta没有学习率参数。相反，它使用参数本身的变化率来调整学习率。
• Adadelta需要两个状态变量来存储梯度的二阶导数和参数的变化。
• Adadelta使用泄漏的平均值来保持对适当统计数据的运行估计。