【数据结构多彩画卷】不要只会普通的二叉树了 , 你听说过用二叉树来排序吗？ 【二叉搜索树】会带给你惊喜 ！！ ！（万字详解）

本篇会加入个人的所谓鱼式疯言

❤️❤️❤️鱼式疯言:❤️❤️❤️此疯言非彼疯言

而是理解过并总结出来通俗易懂的大白话,

小编会尽可能的在每个概念后插入鱼式疯言,帮助大家理解的.

🤭🤭🤭可能说的不是那么严谨.但小编初心是能让更多人能接受我们这个概念 ！！！

引言

二叉搜索树，如数据世界的神秘钥匙，开启高效数据管理之门。它以独特的结构，让数据有序排列，犹如智慧的阶梯，引领我们快速攀登信息高峰。在算法的舞台上，二叉搜索树翩翩起舞，展现出无与伦比的魅力，吸引着无数探索者深入其中，揭开它的神秘面纱。让我们一同踏上这奇妙的数据结构之旅，领略二叉搜索树的精彩之处！

目录

1. 二叉树搜索树

2. 二叉搜索树的实现

3. TreeMap 的使用

一. 二叉树搜索树

1. 二叉搜索的初识

在前面的数据结构——二叉树的章节中， 我们认识到二叉树是一个含有 左右节点的一种非线性的结构 ， 并且我们可以通过 前序遍历， 中序遍历， 后序遍历 的方式来到达每一个节点。

但是在二叉树中 ， 我们只有结构上含有 完全二叉树和满二叉树 的概念， 但是在 存储的数据上并没有规律 。

关于二叉树还不了解的小伙伴可以参考小编的下面三篇二叉树详解全集来理解哦~

详解二叉第一回

详解二叉第二回

详解二叉树完结

而在本篇文章中要认识的一种特殊的二叉树—— 二叉搜索树 ， 是一种在存储的数据值上含有 一定顺序的二叉树 。

鱼式疯言

二叉搜索树，因为在 数值上有一定顺序的 ， 故又称之为 二叉排序树

2. 二叉搜索树的特点

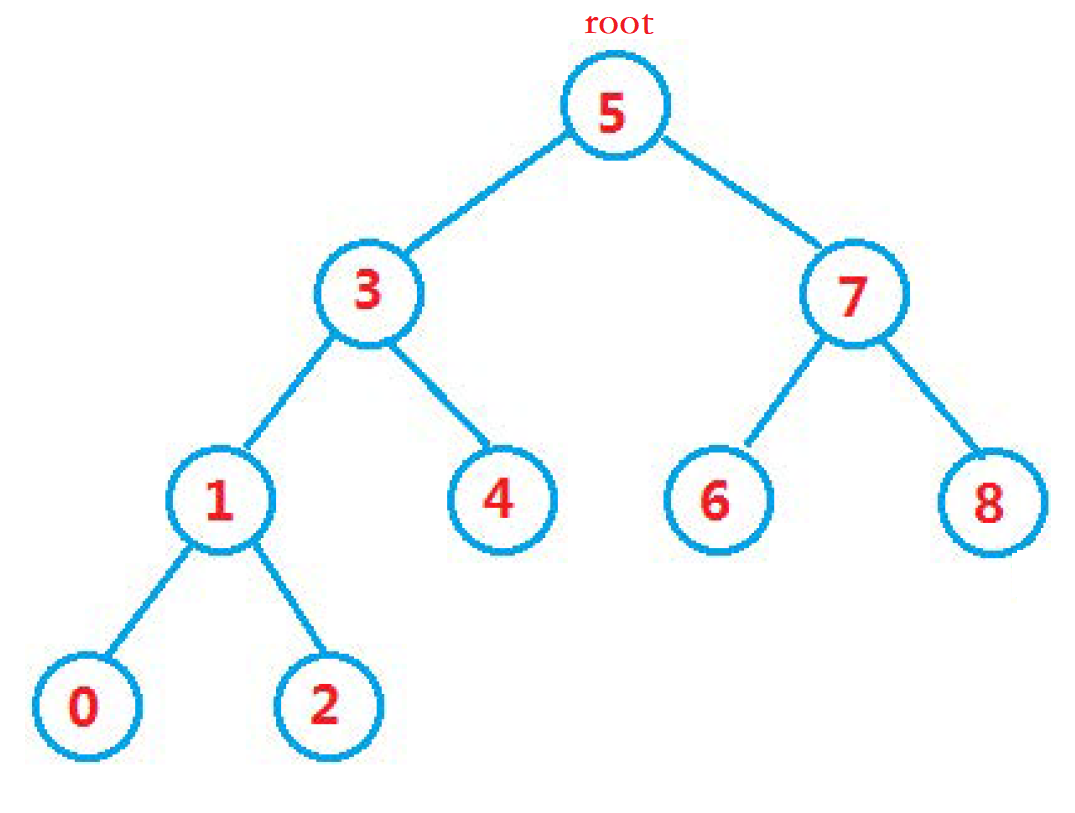
如上图， 这就是一颗二叉搜索树，

小伙伴们可以清楚的看到以下特点： 、

• 在 根节点root 的左子树的 所有节点是小于当前的根节点root 的 val值

• 在 根节点 root 的右子树的 所有节点是大于当前的根节点root 的 val值

• 二叉树的左右子树也都是 二叉搜索树 （递归思想）

• 通过二叉树的 中序遍历 ， 我们就可以得到一组升序的数据： 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8

鱼式疯言

补充说明

• 在二叉搜索树中 ， 规定是不可以存在相同的val值 ， 如果出现相同的值就有可能节点和节点之间的位置是不确定的 ！ ！ ！

了解完二叉搜索的基本含义， 下面让我们真正从代码的角度来一览二叉搜索树的美妙之处~

二. 二叉搜索树的实现

下面讲围绕着二叉搜索树的查 ， 增 ， 删 的三个对于数据结构的基本操作来进行代码的实现。

这时就有小伙伴问了， 改 去哪里了，为啥那么孤立改呢？小编那么偏心吗？

这里小编解释一下哈， 关于改 操作，其实小伙伴们可以思考一下， 是不是和查是一样的啊， 我们只需要调用 查操作 ， 然后 在查操作之后把想要修改的那个节点修改成想要的数据进行赋值语句 即可。 所以小编这里就不赘述了~

1. 查

 public TreeNode search(int key) { TreeNode cur = root; while (cur != null) { if(cur.val < key) { cur = cur.right; }else if(cur.val > key) { cur = cur.left; }else { return cur; } } return null; }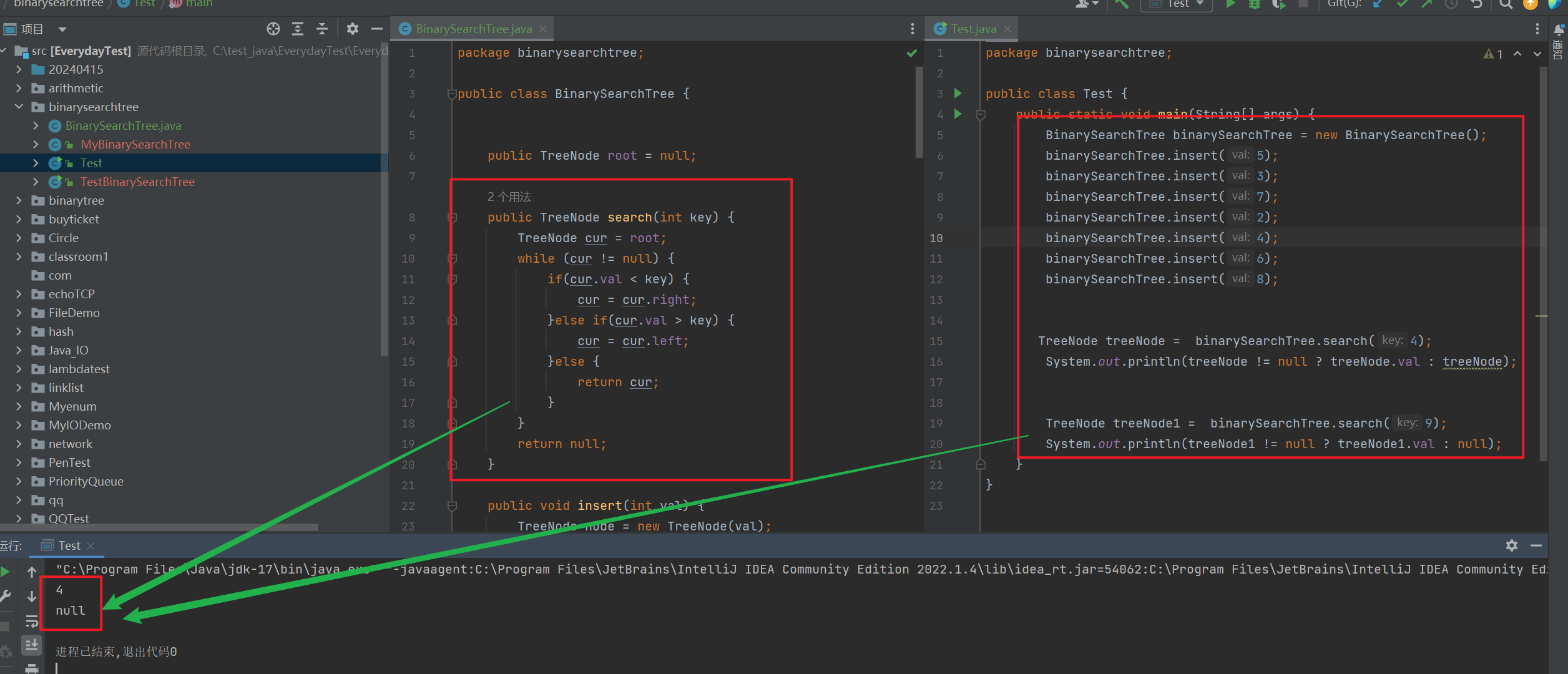

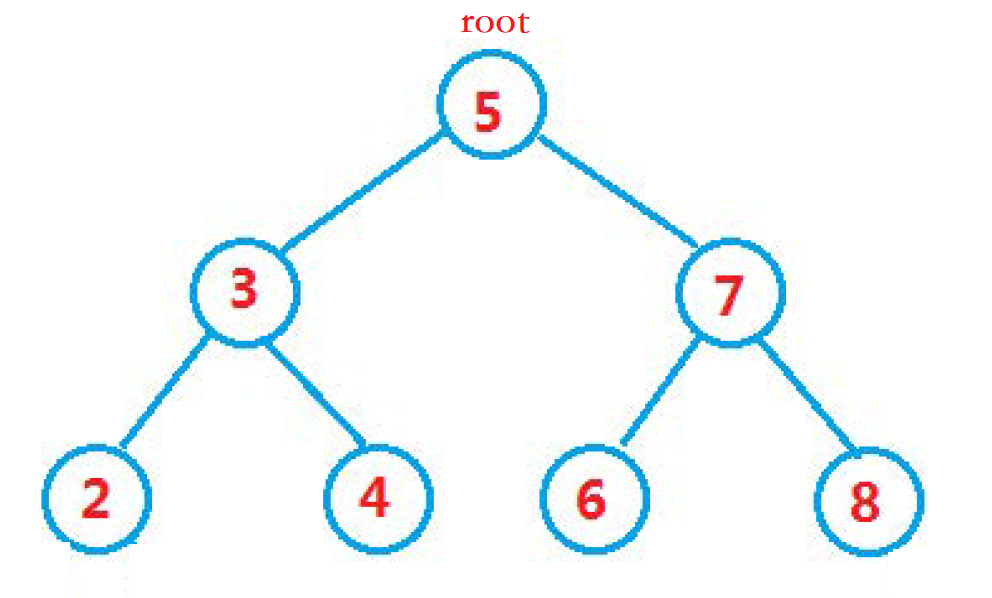
如上图， 上面构造的二叉搜索树， 其实是这样的一个结构。

具体查找的流程可以分为：

1. 从 cur 开始遍历

2. 如果当前 cur 节点的val 值 大于 需要查找的key ， cur 就向左节点 走

3. 如果当前 cur 节点的val 值 小于 需要查找的 key ， cur 就往右节点 走

4. 直到最终 cur 节点的等于 val ， 就返回 当前节点 。

5. 如果遍历完 整个二叉搜索树都没有寻找到结果 ， 就说明当前树中没有该值， 就 返回null 。

如下图流程：

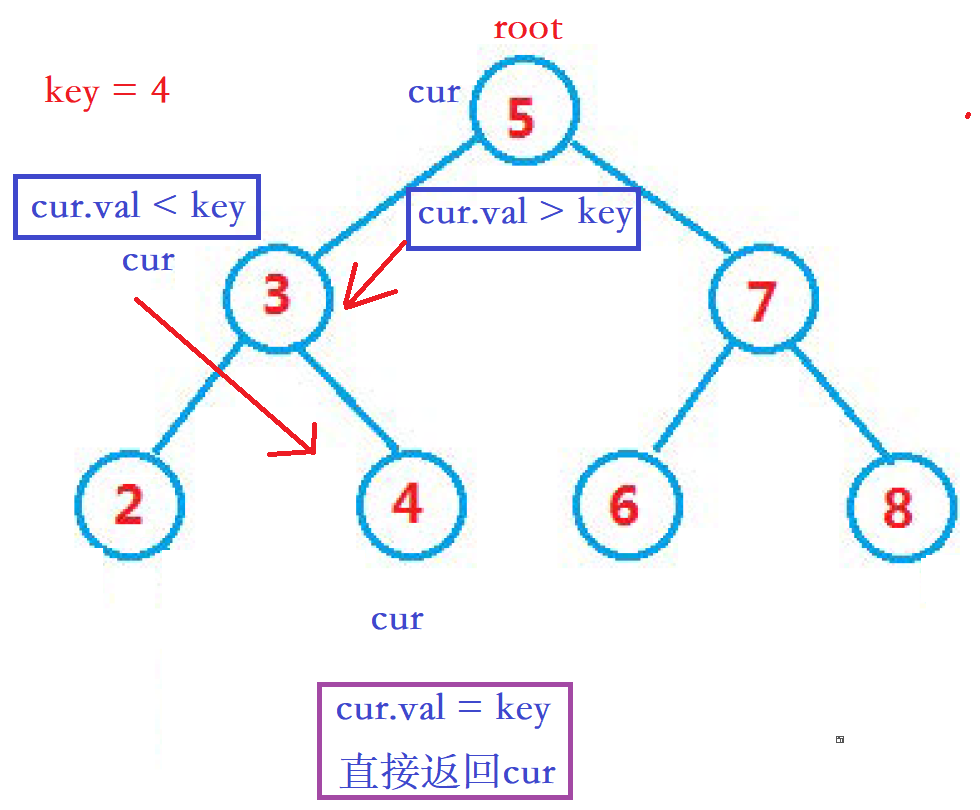
鱼式疯言

从上面的查找中， 可以理解到可以根据 二叉搜索树 自身 左小右大 的特点， 确定该位置是往左走还是往右走， 从而 快速的查找到需要查找的数据 。

2. 增

public void insert(int val) { TreeNode node = new TreeNode(val); if(root == null) { root = node; return; } TreeNode cur = root; TreeNode parent = null; while (cur != null) { if(cur.val < val) { parent = cur; cur = cur.right; }else if(cur.val > val) { parent = cur; cur = cur.left; }else { return; } } //parent 指向的节点 就是 需要插入的节点位置 的 父亲节点 if(parent.val > val) { parent.left = node; }else { parent.right = node; } }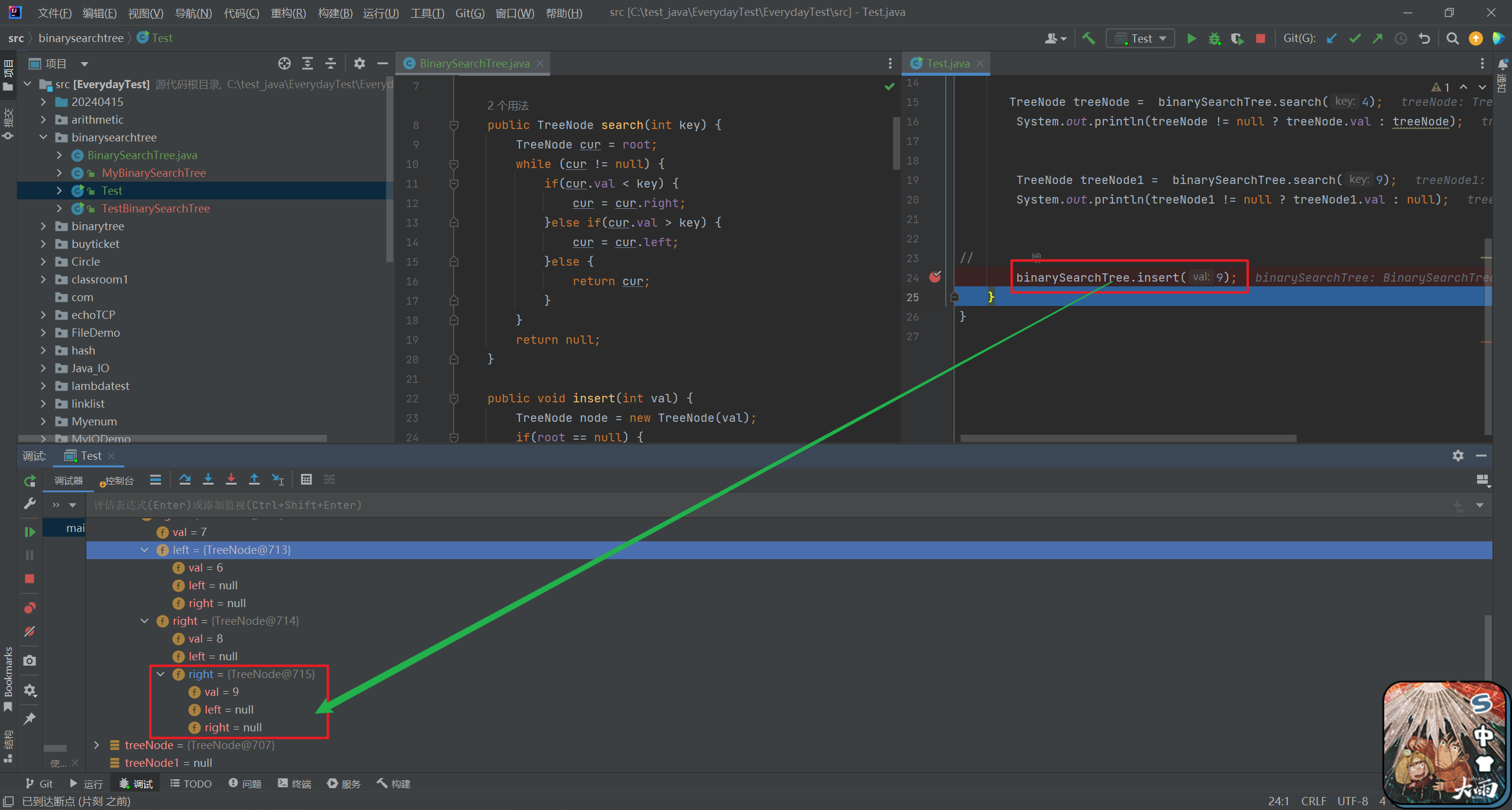

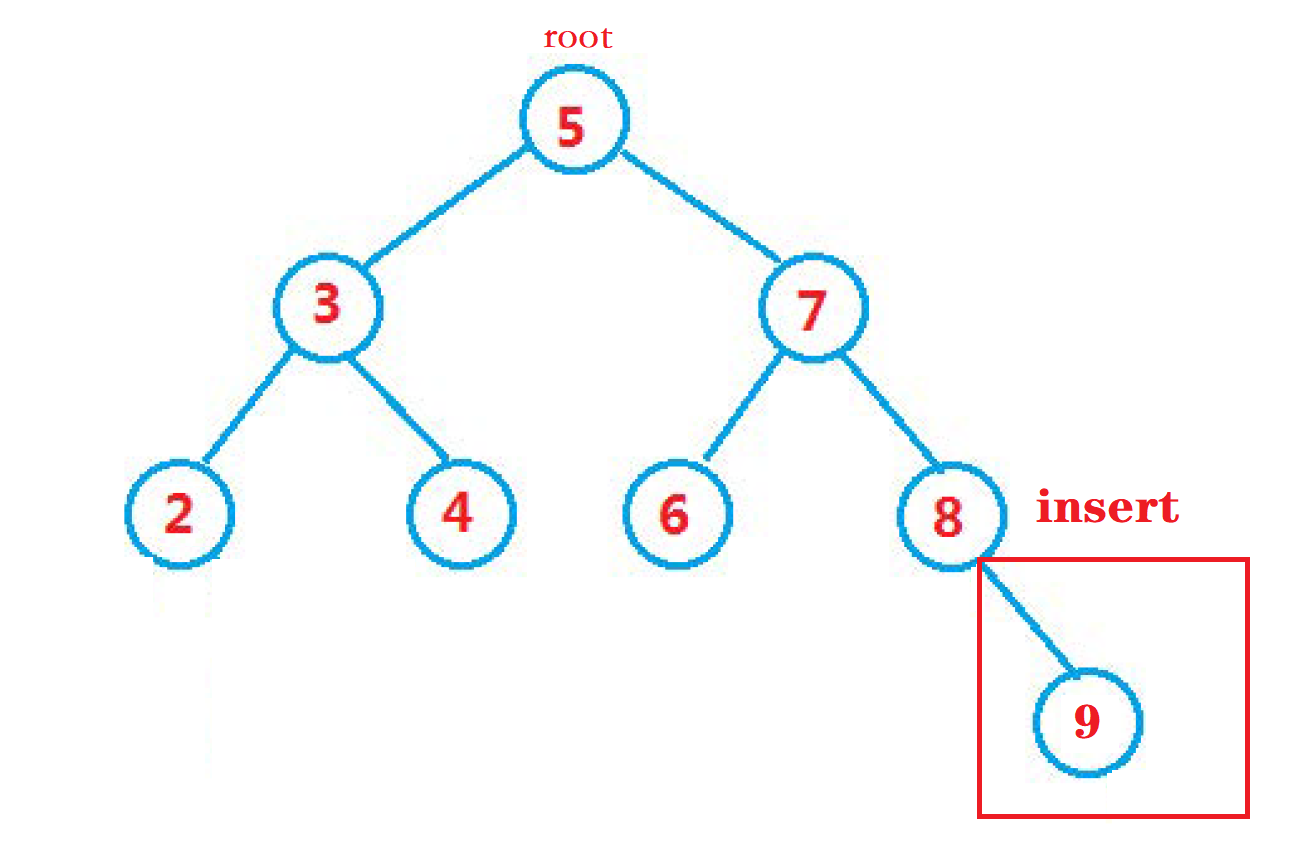
操作流程：

1. 首先用cur 表示当前节点， parent 记录cur 的上一个节点。

2. 如果当前 cur 节点的val 值 大于 需要查找的key ， cur 就向左节点 走。

3. 如果当前 cur 节点的val 值 大于 需要查找的key ， cur 就向左节点 走。

4. 如果 cur 节点的等于 val ， 就 退出方法， 添加失败。

5. 最终遍历结束后 cur 为 null， parent 记录着 最终位置 。判断 其val 值大小来插入到 parent 的左节点还是右节点进行插入。

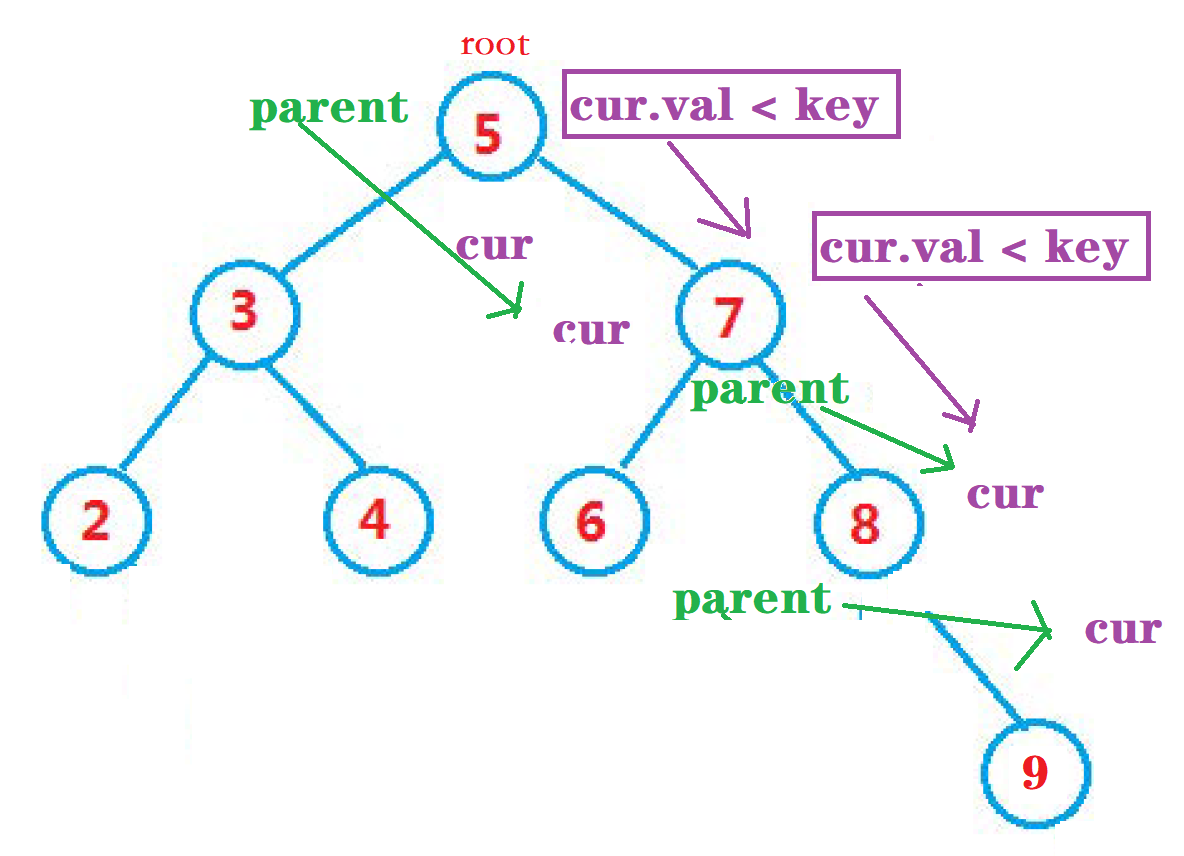
鱼式疯言

注意事项：

• 注意这里不要 添加重复的数据 , 如果 添加重复的元素就无法确定新添加的重复元素在是原有元素的左子树还是右子树， 就很容易 出现BUG（下面的TreeMap就会出现）

3. 删（难点）

 public void remove(int key) { TreeNode parent = null; TreeNode cur = root; while (cur != null) { if(cur.val < key) { parent = cur; cur = cur.right; }else if(cur.val > key) { parent = cur ; cur = cur.left; }else { removeNode(parent,cur); return; } } } private void removeNode(TreeNode parent,TreeNode cur) { if(cur.left == null) { if(cur == root) { root = cur.right; }else if(cur == parent.left) { parent.left = cur.right; }else { parent.right = cur.right; } }else if(cur.right == null) { if(cur == root) { root = cur.left; }if(cur == parent.left) { parent.left = cur.left; }else { parent.right = cur.left; } }else { TreeNode target = cur.right; TreeNode targetP = cur; while (target.left != null) { targetP = target; target = target.left; } cur.val = target.val; if(target == targetP.left) { targetP.left = target.right; }else { targetP.right = target.right; } } }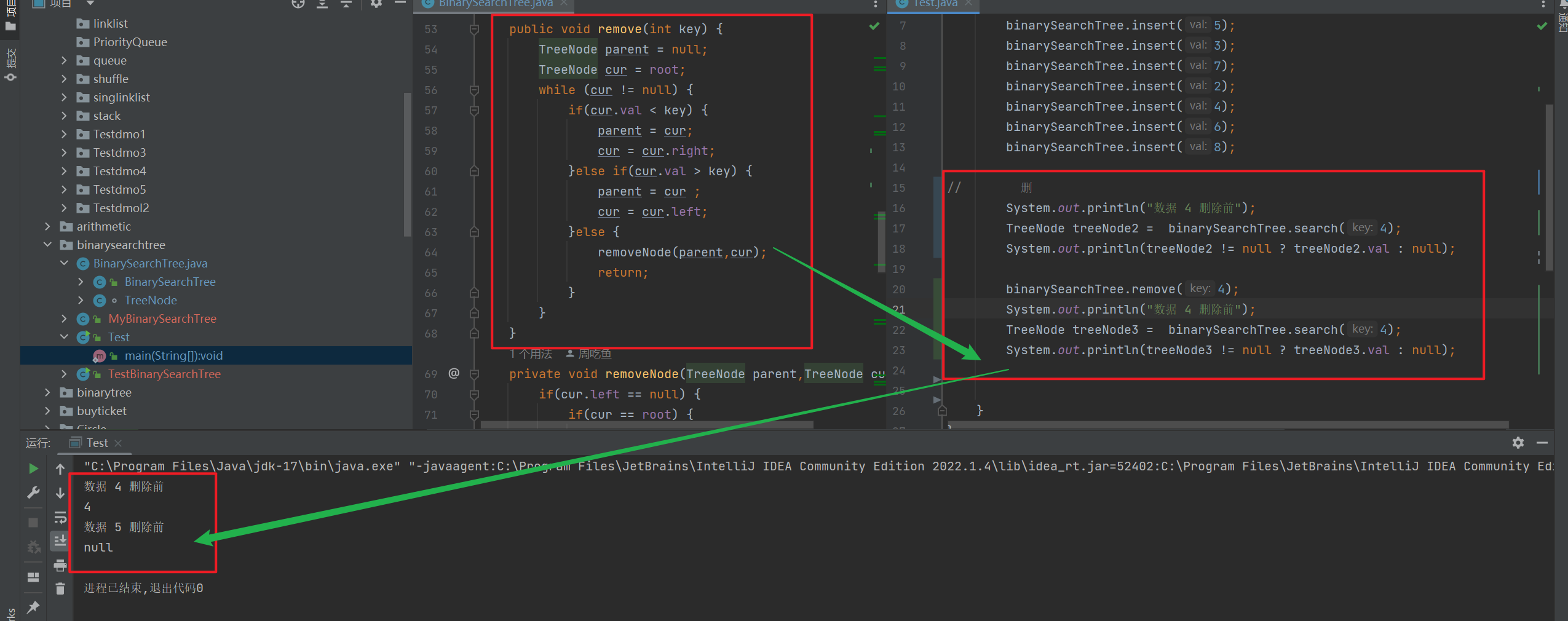

如上图：

对于 二叉搜索树删除 的过程中， 是有一定难度的， 不是说 本身的删除操作难， 而是 需要考虑的情况比较多， 下面小编将 从三种情况来考虑进行删除操作 ：

设待删除的节点为 cur， 待删除的双亲节点为 parent ：

• cur.left = null;

• cur.right = null;

• cur.left != null && cur.right != null

. cur.left = null

情况一 ： cur.left == null && cur = root

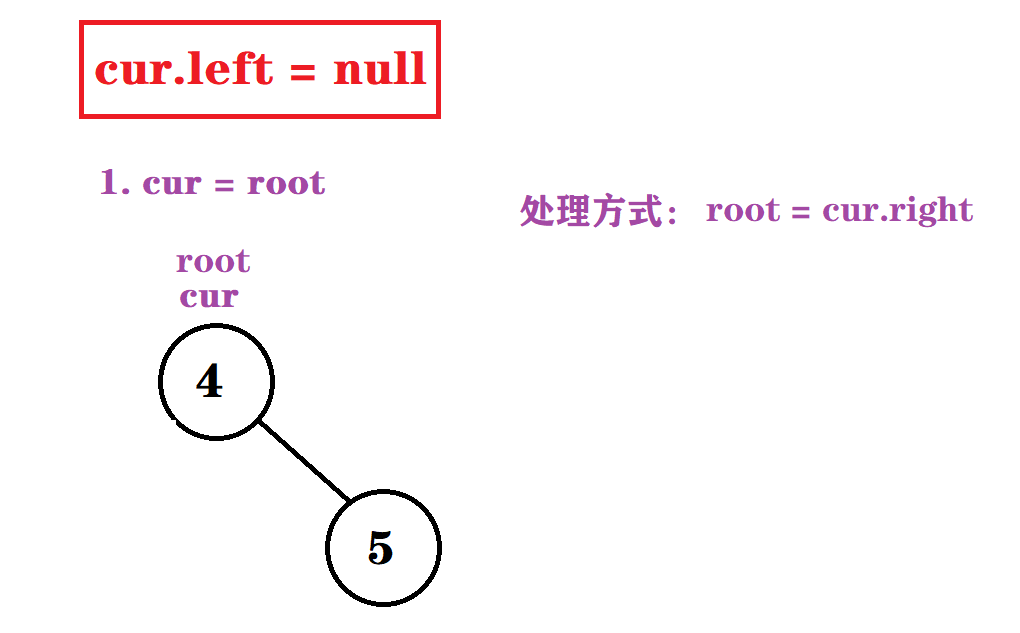
情况二 ： cur.left == null && parent.left = cur

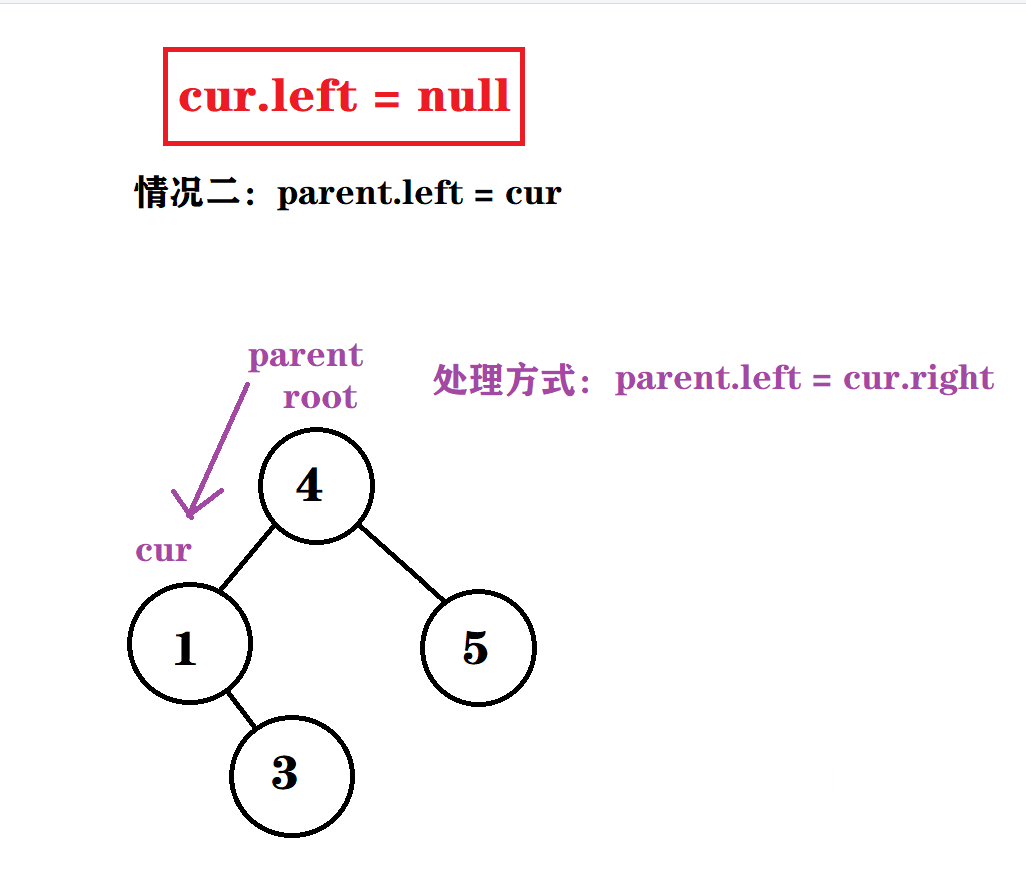
情况三 ： cur.left == null && parent.right = cur

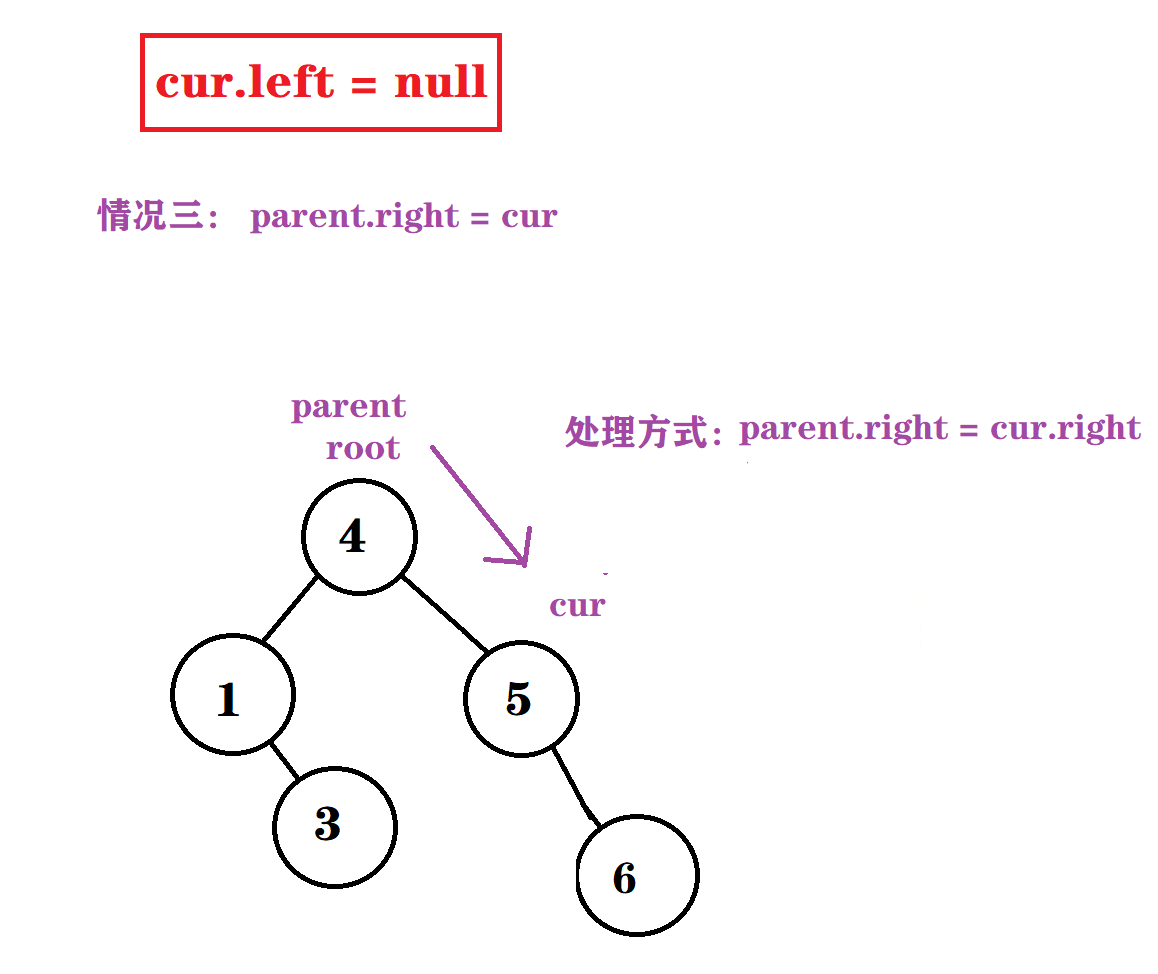
. cur.right = null

情况一： cur.right = null && cur = root

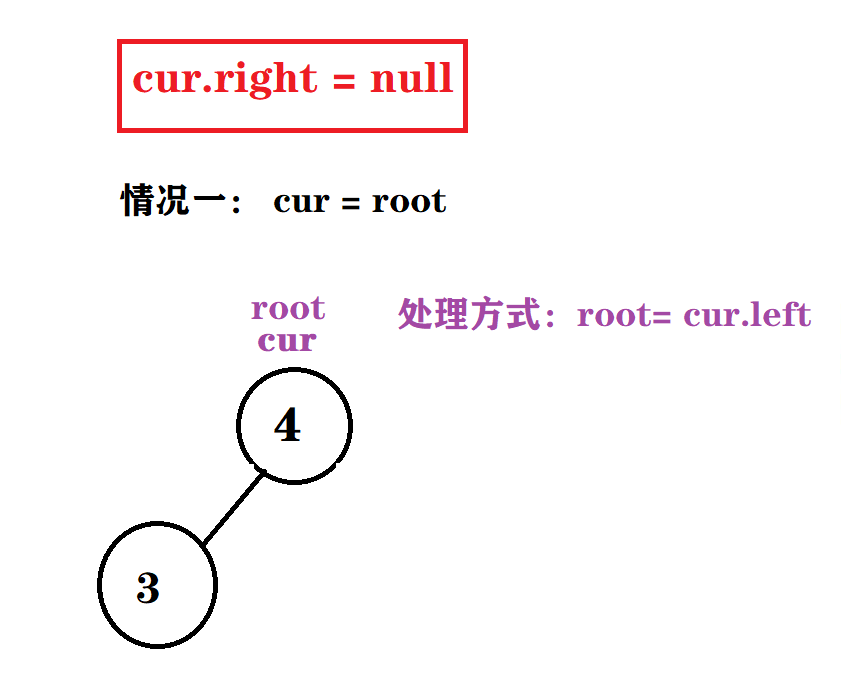
情况二： cur.right = null && parent.left = cur

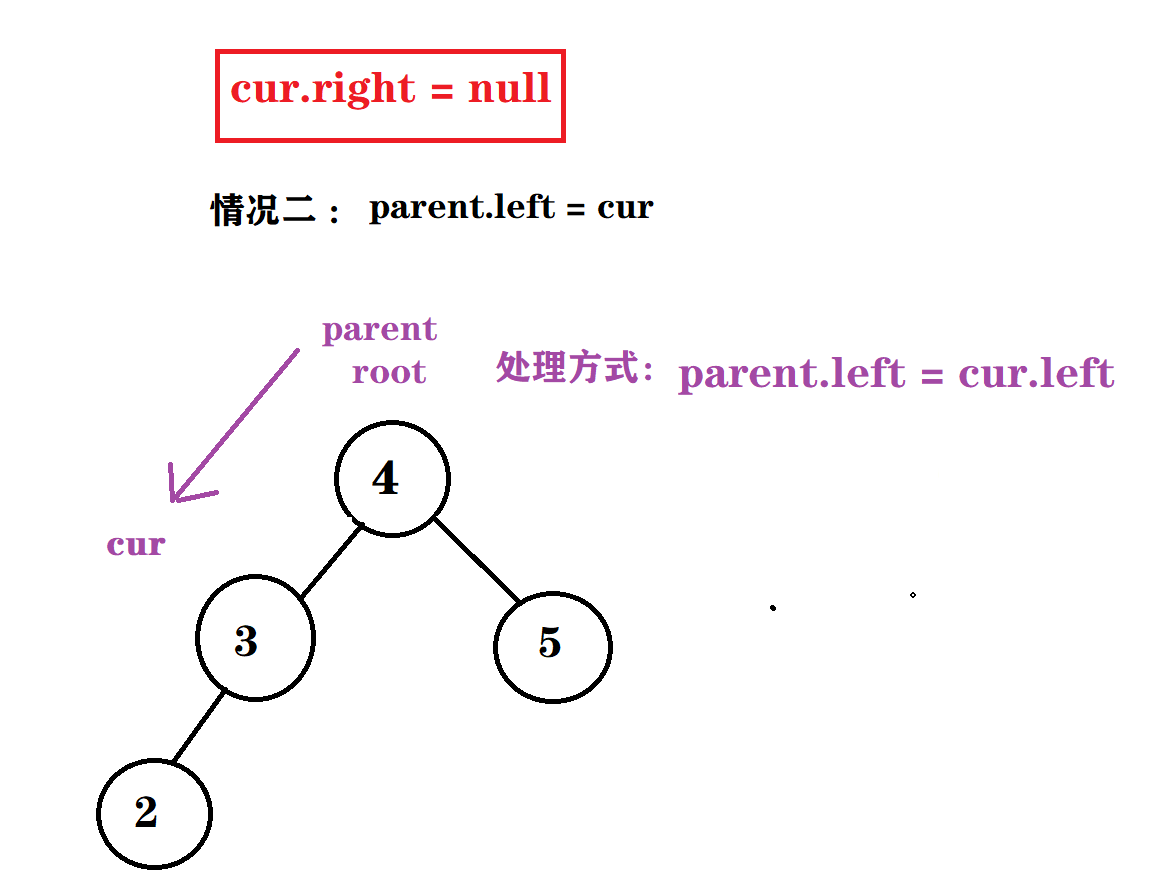
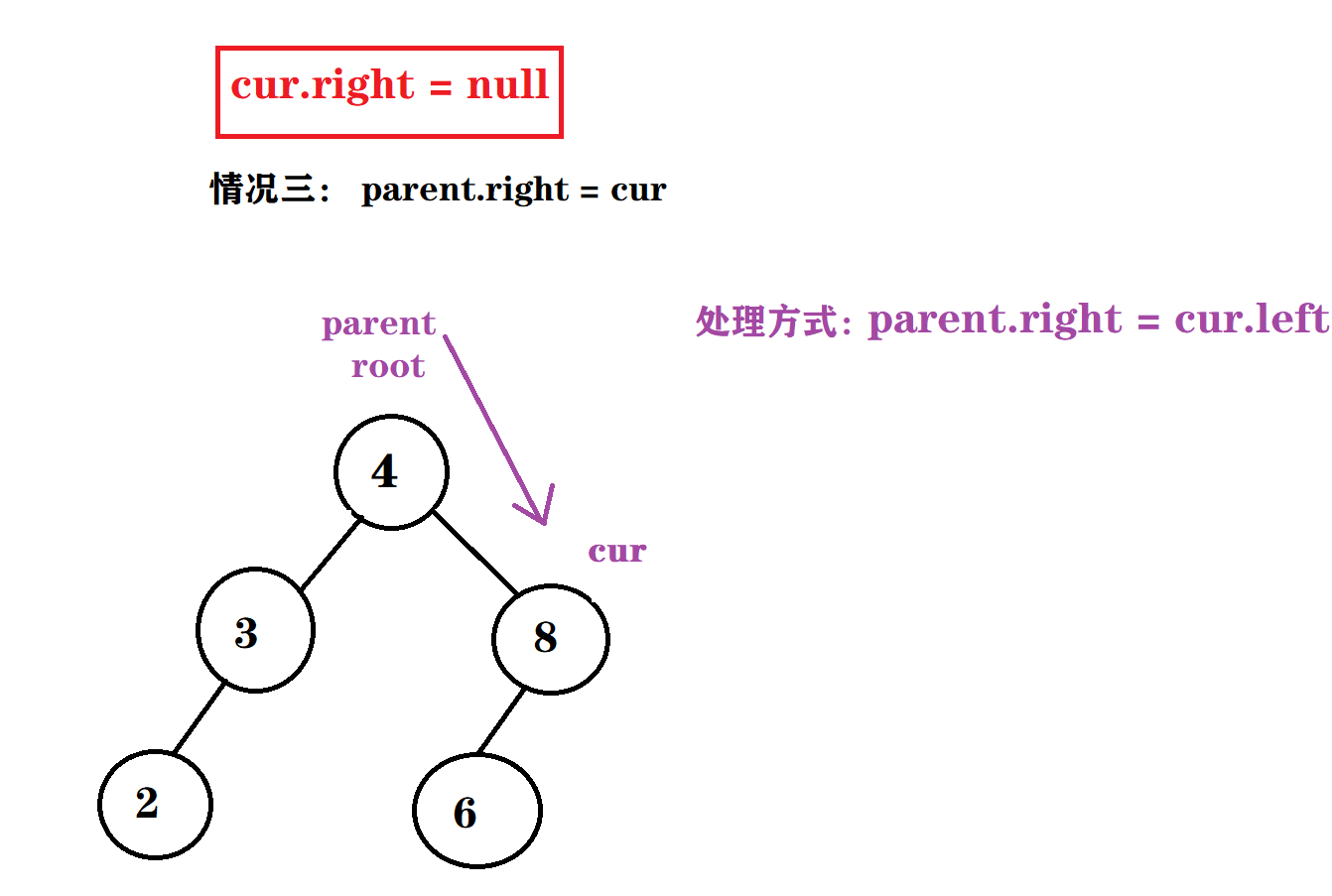
情况三 ： cur.right = null && parent.right = cur

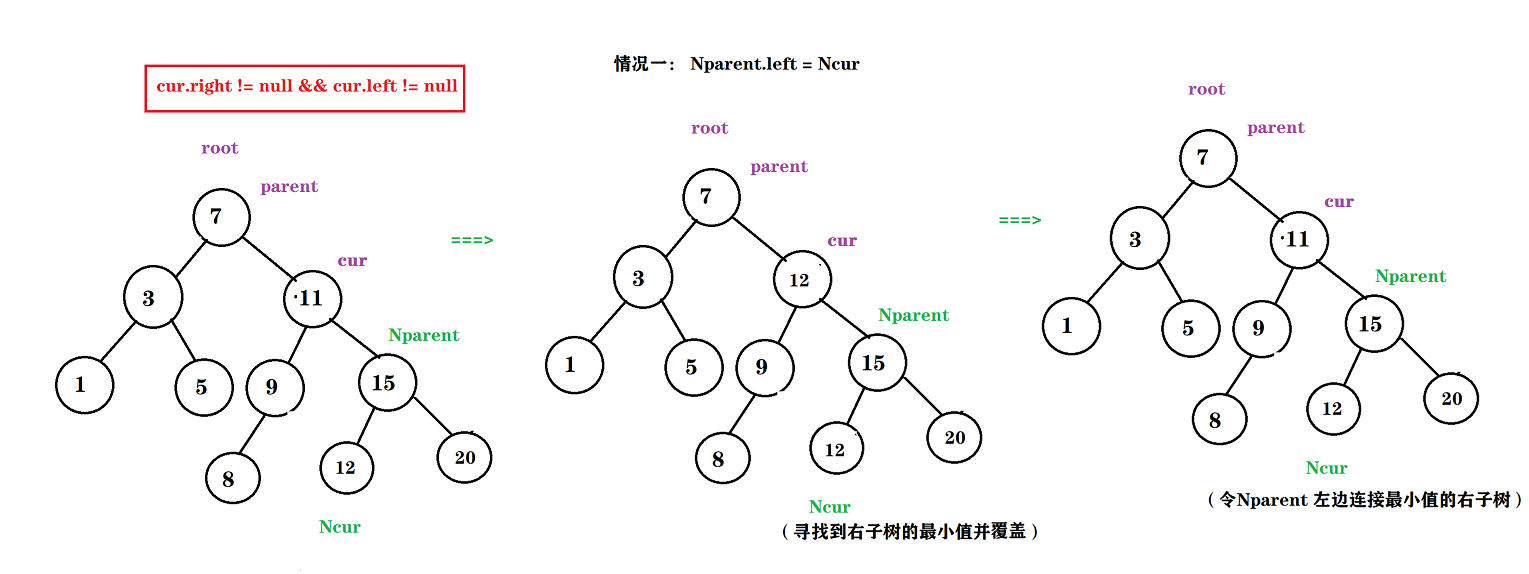
. cur.left != null && cur.right != null

这种情况是最复杂的， 因为需要删除的节点左右两边都还连着数据， 所以我们的方式是需要 cur右子树的最小值（右子树最左边的节点） 或 cur左子树的最大值（左子树最右边的节点） 。

这里小编就介绍这种 cur右子树最小值 的方式来 删除cur 节点。

如果要需要再假设两个变量： Ncur 为 右子树的最小值 ， Nparent 为 右子树最小值的双亲节点。

于是就分下面两种情况考虑：

情况一 ： Nparent.left = Ncur

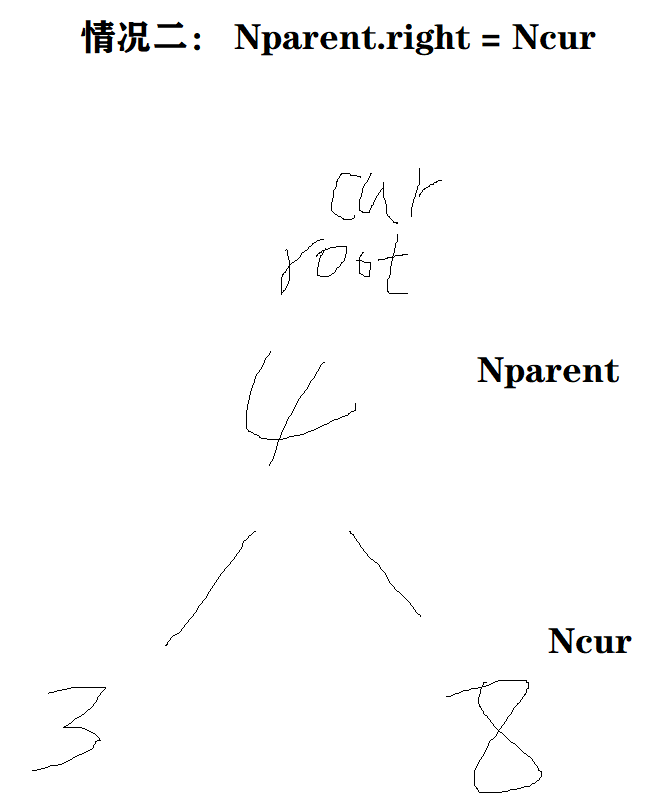
情况二 ： Nparent.right = Ncur

4. 二叉搜索树全代码展示

package binarysearchtree;public class BinarySearchTree { public TreeNode root = null; public TreeNode search(int key) { TreeNode cur = root; while (cur != null) { if(cur.val < key) { cur = cur.right; }else if(cur.val > key) { cur = cur.left; }else { return cur; } } return null; } public void insert(int val) { TreeNode node = new TreeNode(val); if(root == null) { root = node; return; } TreeNode cur = root; TreeNode parent = null; while (cur != null) { if(cur.val < val) { parent = cur; cur = cur.right; }else if(cur.val > val) { parent = cur; cur = cur.left; }else { return; } } //parent 指向的节点 就是 需要插入的节点位置 的 父亲节点 if(parent.val > val) { parent.left = node;  }else { parent.right = node; } } //key = 10; public void remove(int key) { TreeNode parent = null; TreeNode cur = root; while (cur != null) { if(cur.val < key) { parent = cur; cur = cur.right; }else if(cur.val > key) { parent = cur ; cur = cur.left; }else { removeNode(parent,cur); return; } } } private void removeNode(TreeNode parent,TreeNode cur) { if(cur.left == null) { if(cur == root) { root = cur.right; }else if(cur == parent.left) { parent.left = cur.right; }else { parent.right = cur.right; } }else if(cur.right == null) { if(cur == root) { root = cur.left; }if(cur == parent.left) { parent.left = cur.left; }else { parent.right = cur.left; } }else { TreeNode target = cur.right; TreeNode targetP = cur; while (target.left != null) { targetP = target; target = target.left; } cur.val = target.val; if(target == targetP.left) { targetP.left = target.right; }else { targetP.right = target.right; } } }} class TreeNode { public int val; public TreeNode left; public TreeNode right; public TreeNode(int val) { this.val = val; }}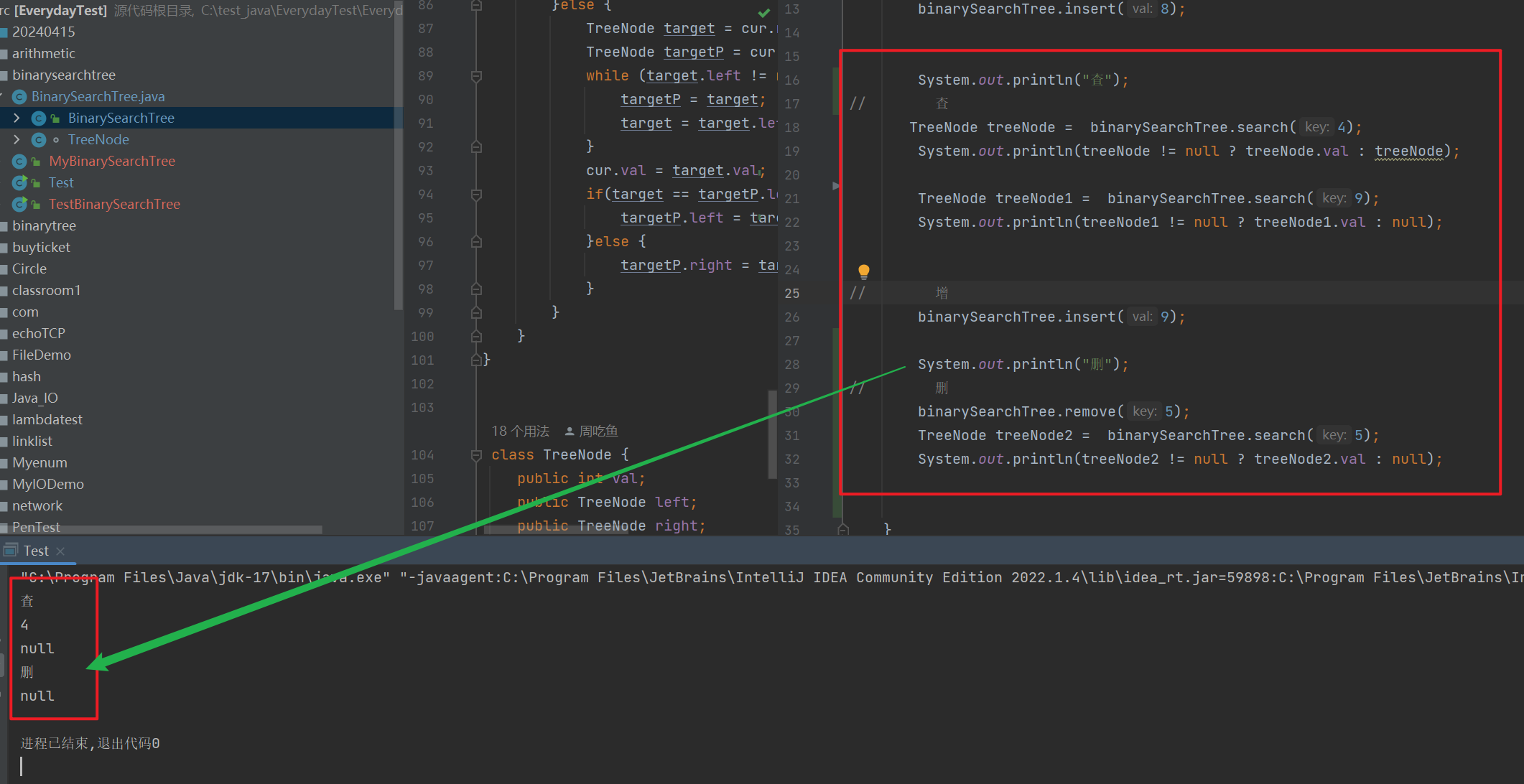

如上图， 这就是二叉搜索树的常见的三种操作了，关于需要更一步学习搜索树的小伙伴，在后期小编将推出更难的系列——红黑树，B树等…

敬请期待哦~

三. TreeMap 的使用

1. TreeMap 的引入

关于 TreeSet 和 TreeMap , 其实是java底层利用红黑树去实现的 Set 和 Map 的接口，

红黑树的是在 二叉搜索树的基础上加上 一些颜色辨别和调整实现一颗近乎平衡二叉树， 是 比普通二叉搜索树效率更高的一颗二叉树 。

而在本文中不讲解如何实现红黑树， 而是 简单的讲解 对于 TreeMap 的具体用法（后序会详细重点讲解）。

2. TreeMap 和 HashMap 的区别

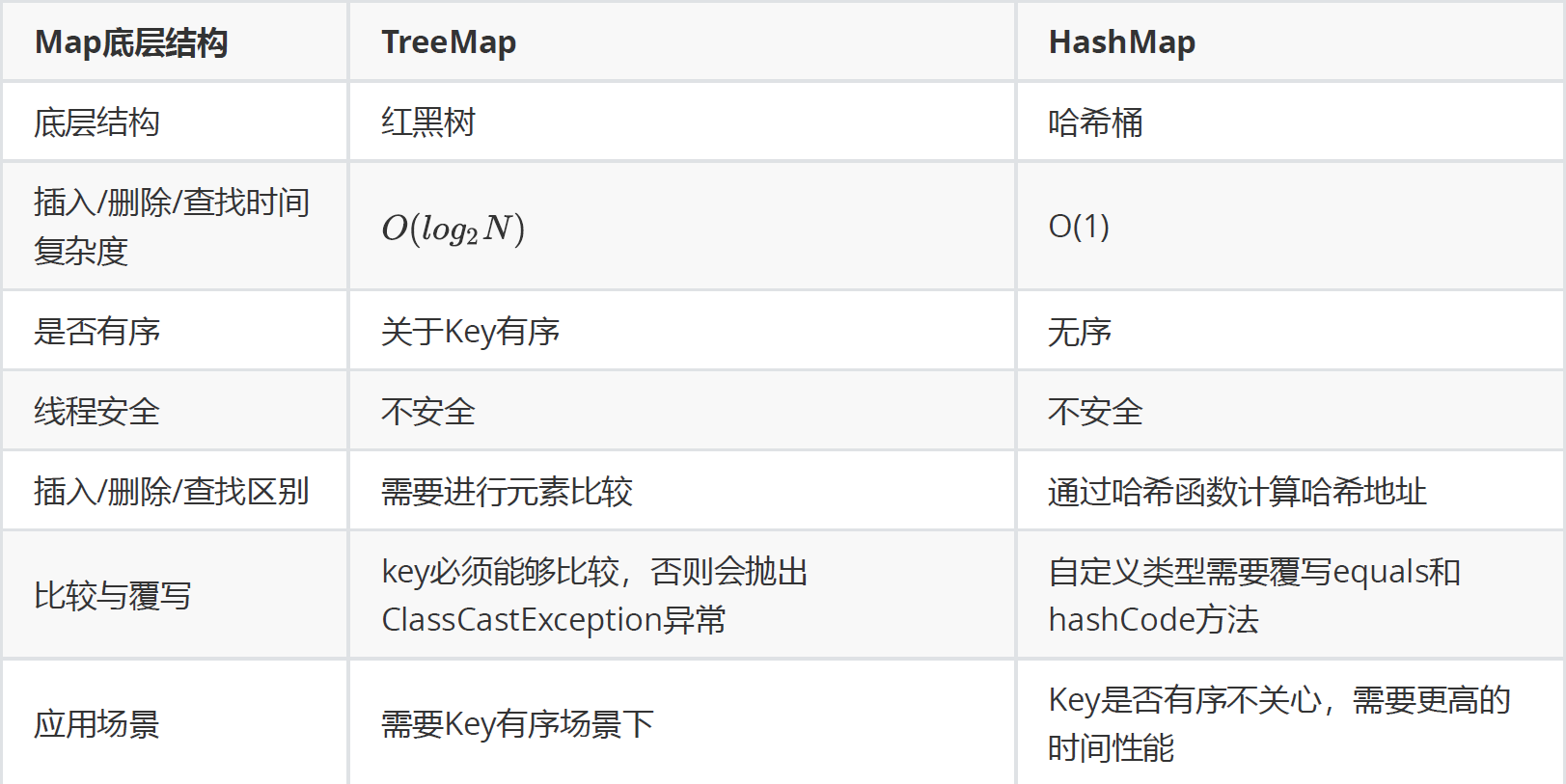
如上图：

为什么说不是重点讲解用法， 因为在 HashMap 中已经讲解了相同的用法， 可以那么说吧。

• 操作的时间复杂度 ：TreeMap 是 O（n） ， 而HashMap 是 O（1） 的。

• 其实 HashMap 和 TreeSet 最本质的区别， 就在于 TreeMap 只是一颗搜索树， TreeMap是需要当数据操作时就需要对 数据的比较， 而 HashMap 不底层只是 一个数组不需要比较 。

2. 基本类型的使用

package binarytree;import java.util.Map;import java.util.TreeMap;public class Demo { public static void main(String[] args) { Map<Integer,String> map = new TreeMap<>(); map.put(12, \"shuaige\"); map.put(25, \"meinv\"); map.put(76, \"dalao\"); System.out.println(25); }}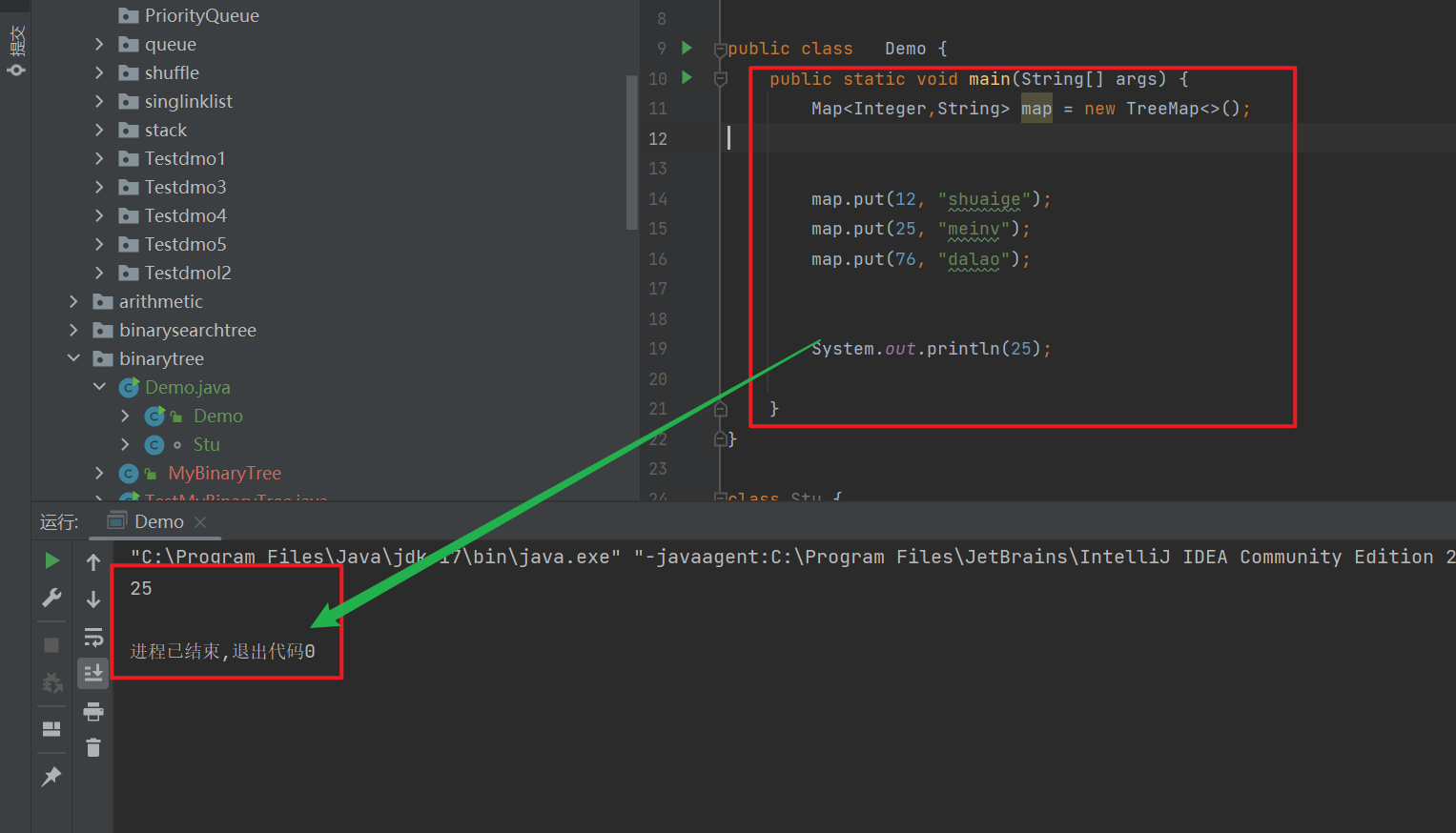

如上图，

基本类型 的使用和 HashMap 的使用是一致的， 都是通过键值对 Key- Value 的方式存储的， 并且通过 Key 的方式可以访问到对应的 Value 。

如果是 普通的基本类型 不需要 指定特别的比较方式 ， 因为 属性（成员变量）只有一个 。

但是如果是 具体对象的话， 由于 成员变量比较多 ， 就需要指定 比较方式 ， 否则编译器不知道要通过 哪个变量来进行比较 来 确定左子树还是右子树 。

鱼式疯言

补充说明：

如果 不指定比较方式 ， 就会抛出如下 异常

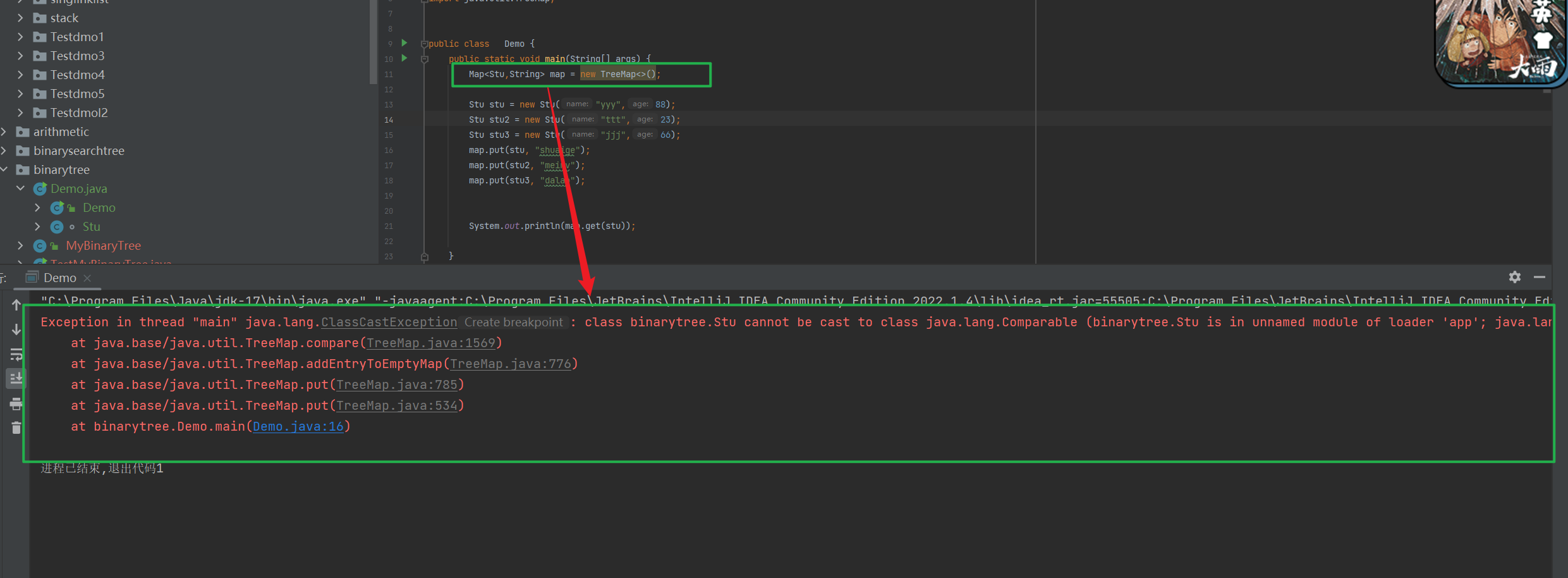
3. 比较方式

搜索树需要建立 比较方式， 建立比较方式就需要 比较方法，关于比较方法， 小编介绍两种比较方法的方式：

• Comparator 的 比较器 的比较

• Comparable的 比较接口 的实现

. Comparator 比较

package binarytree;import java.util.Comparator;import java.util.Map;import java.util.TreeMap;public class Demo { public static void main(String[] args) { Map<Stu,String> map = new TreeMap<>(new Comparator<Stu>() { @Override public int compare(Stu o1, Stu o2) { return Integer.compare(o1.age, o2.age); } }); Stu stu = new Stu(\"yyy\",88); Stu stu2 = new Stu(\"ttt\",23); Stu stu3 = new Stu(\"jjj\",66); map.put(stu, \"shuaige\"); map.put(stu2, \"meinv\"); map.put(stu3, \"dalao\"); System.out.println(map.get(stu)); }}class Stu { int age ; String name; public Stu( String name, int age) { this.age = age; this.name = name; }}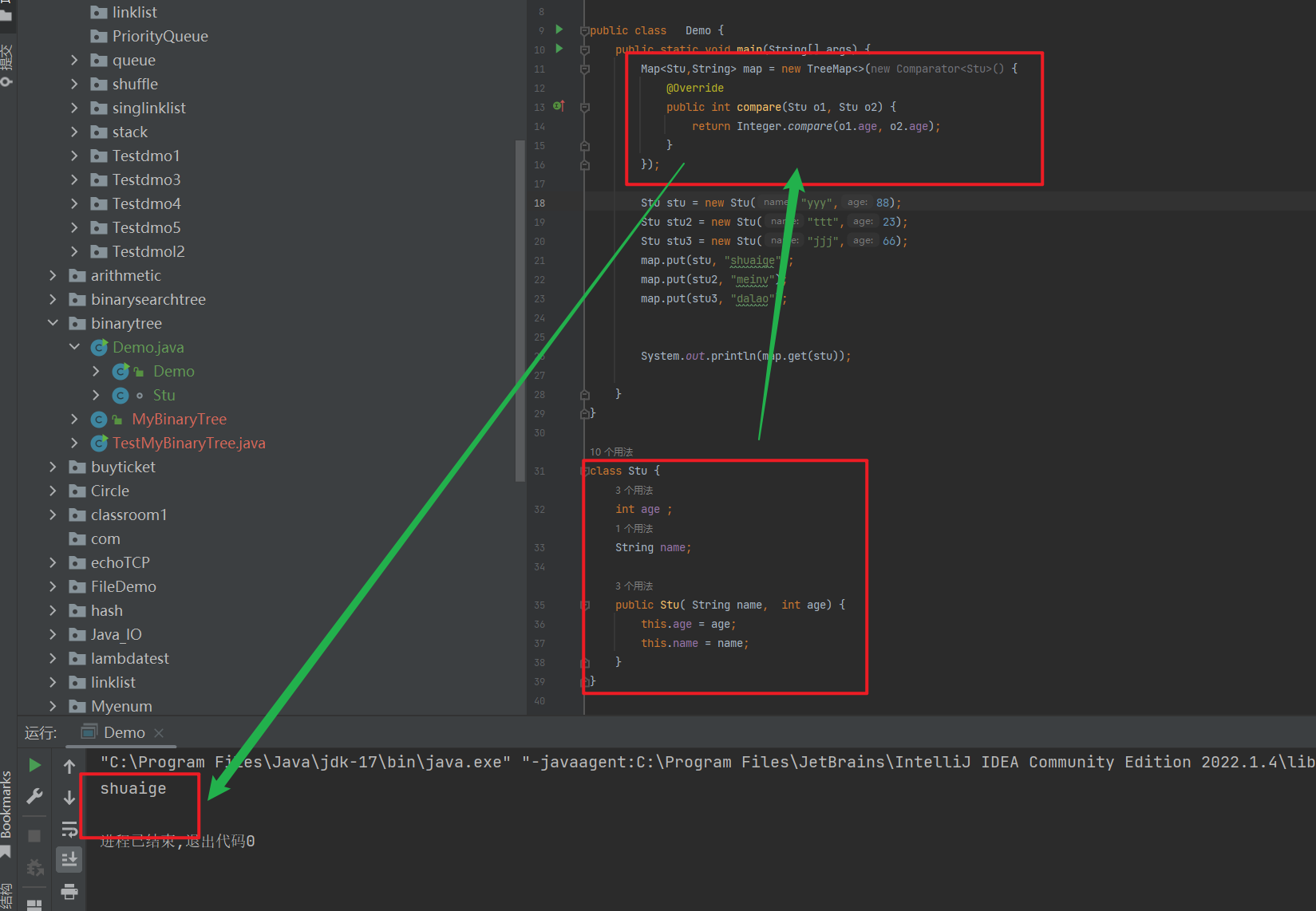

如上图， 我们通过匿名内部类的方式来实现我们的比较器， 通过 比较器就确定需要用 age 这个成员变量来进行比较。

或者也可以用 name 这个成员变量来指定也可以, 根据 具体的需求场景 。

. Comparable 比较

package binarytree;import java.util.Map;import java.util.TreeMap;public class Demo { public static void main(String[] args) { Map<Stu,String> map = new TreeMap<>(); Stu stu = new Stu(\"yyy\",88); Stu stu2 = new Stu(\"ttt\",23); Stu stu3 = new Stu(\"jjj\",66); map.put(stu, \"shuaige\"); map.put(stu2, \"meinv\"); map.put(stu3, \"dalao\"); System.out.println(map.get(stu)); }}class Stu implements Comparable<Stu>{ int age ; String name; public Stu( String name, int age) { this.age = age; this.name = name; } @Override public int compareTo(Stu o) { return this.age-o.age; }}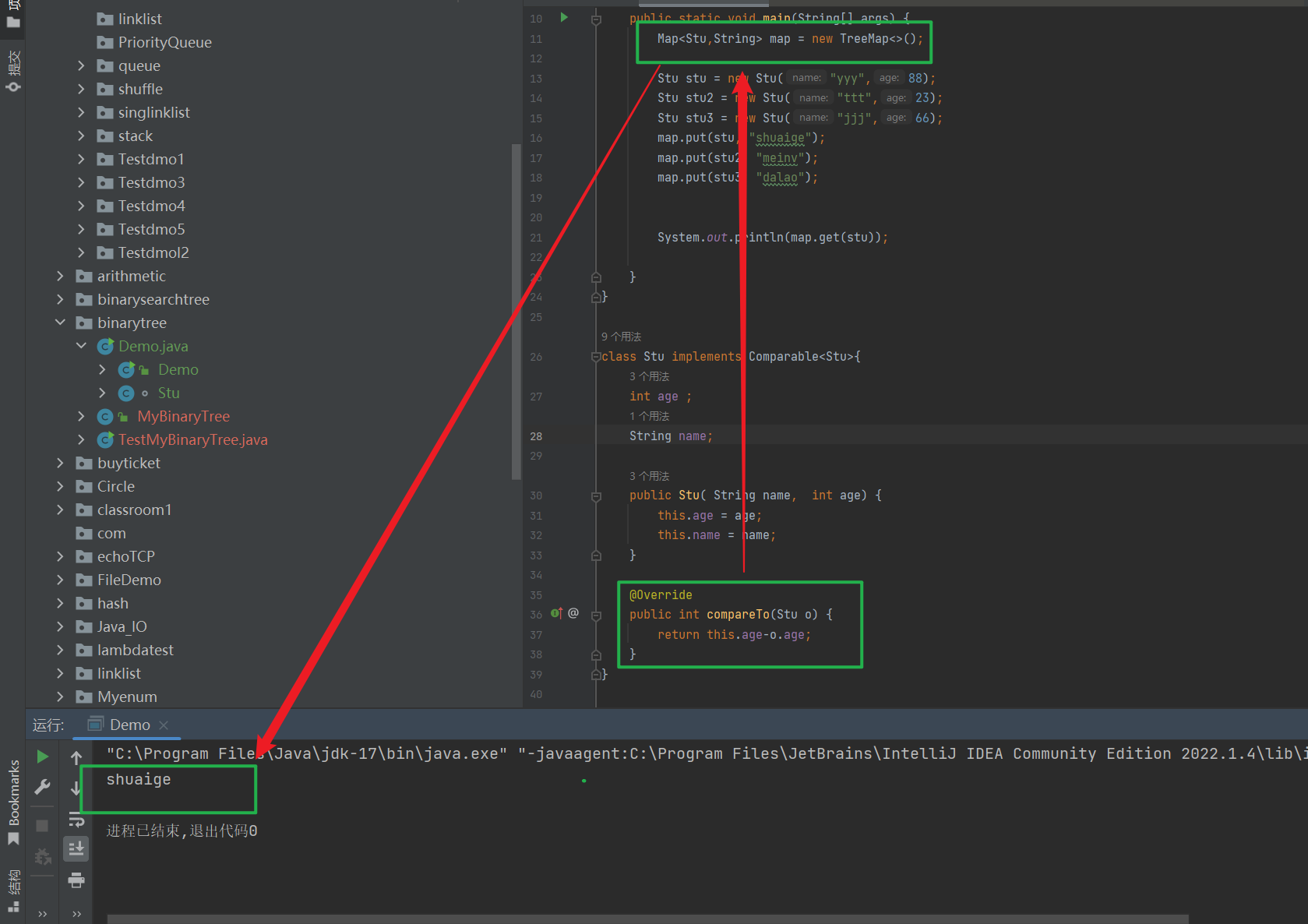

上述过程是通过实现 Comparable 的接口 来确定比较方式。

鱼式疯言

补充细节：

这里小编要提上一嘴：

1. 注意不要在 Key的比较方式中添加 相同的数据， 否则就会出现以下的 BUG 。

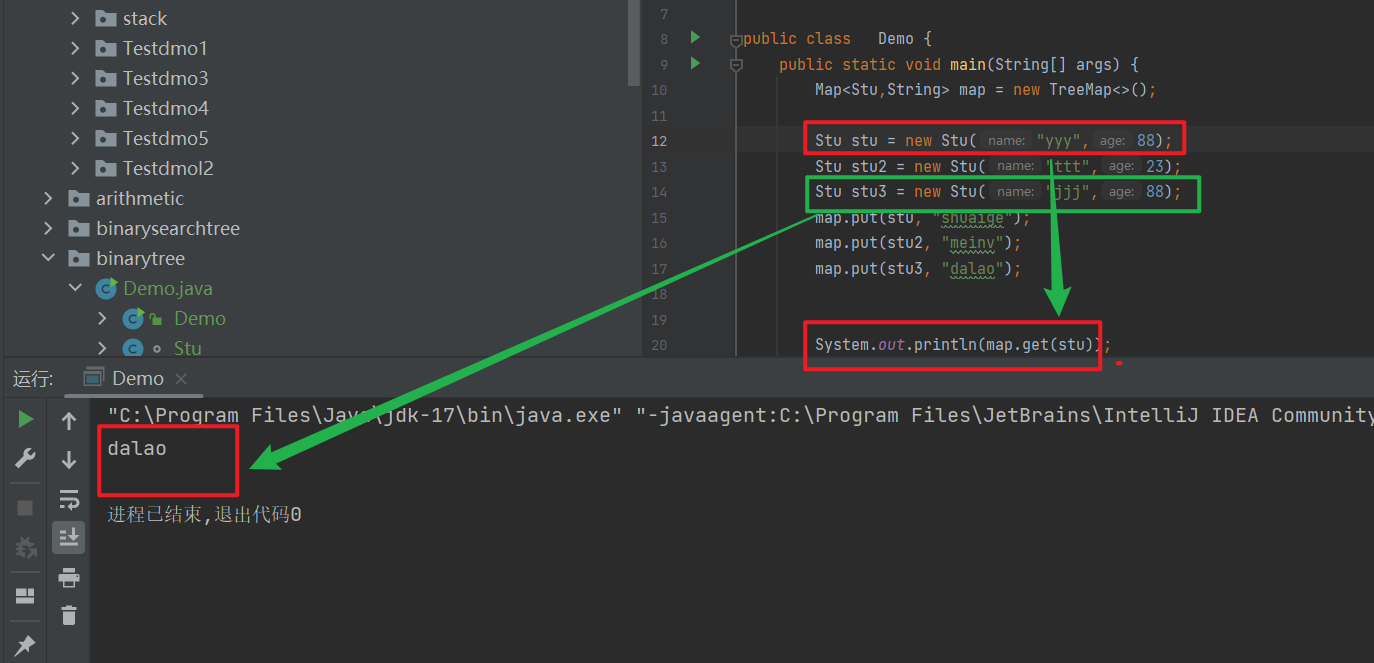
2. 可以用lambda 表达式的形式简化 匿名内部类实现 Comparator 的比较器：

 Map<Stu,String> map = new TreeMap<>((a,b)->{ return a.age-b.age; });

故: 上面是小编主要就是围绕 数据比较 来讲， 其实的使用方法 HashMap 并且 HashSet 和 TreeSet 的使用方式也都是 使用是一模一样的 ， 唯一的区别就在于上面的 比较方法 ， 小编在这里就 不赘述了 。

使用不明确的小伙伴，参考以下文章哦~

HashMap 与 HashSet 的详解文章

总结

• . 二叉树搜索树: 初识二叉搜索树本质上是一颗排序树： 左子树都小于根节点 ， 右子树都大于根节点 的一颗特殊的二叉树。

• . 二叉搜索树的实现： 二叉树的实现主要围绕 查， 增， 改的三部曲 来实现， 并且对于 删操作 这个难点主要分为三种情况考虑： cur.left = null ， cur.right = null ， cur.left != null && cur.right != null ， 这三种情况来考虑。

• . TreeMap 的使用: 主要围绕着 比较方法： Comparator 的比较器实现 ，Comparable的接口实现， 其他的方法都是一样一样的~

如果觉得小编写的还不错的咱可支持 三连 下 (定有回访哦) , 不妥当的咱请评论区 指正

希望我的文章能给各位宝子们带来哪怕一点点的收获就是 小编创作 的最大 动力 💖 💖 💖