【Leetcode:面试经典150题】(1-10题)解析
一、内容描述
Hello!今天不再摆烂开始学习,哦莫。作者是python解法噢(*╹▽╹*)
面试经典 150 题 - 学习计划 - 力扣(LeetCode)全球极客挚爱的技术成长平台
二、练习
88. 合并两个有序数组
方法一:直接合并然后排序
排序(sort、sorted)
sort在排序时,是在对原列表本身进行改变,不需要另外一个空列表来进行接收,没有返回值。sorted在排序时,并不是对原列表本身进行改变,这时需要一个空列表进行接收排序后的列表,有返回值。
LeetCode:
class Solution(object): def merge(self, nums1, m, nums2, n): nums1[m:]=nums2 nums1.sort() 完整版:
def merge(nums1, m, nums2, n): nums1[m:] = nums2[:n] nums1.sort() return nums1# 获取用户输入nums1_input = input(\"请输入nums1(以空格分隔的整数,后n个为0):\")m = int(input(\"请输入m(nums1的有效元素个数):\"))nums2_input = input(\"请输入nums2(以空格分隔的整数):\")n = int(input(\"请输入n(nums2的元素个数):\"))# input输入的是字符串,需要转换输入为列表nums1 = list(map(int, nums1_input.split()))nums2 = list(map(int, nums2_input.split()))# 合并数组merge(nums1, m, nums2, n)# 输出结果print(\"合并后的nums1:\", nums1)复杂度分析
时间复杂度:O((m+n)log(m+n))。
排序序列长度为 m+n,套用快速排序的时间复杂度即可,平均情况为 O((m+n)log(m+n))。
空间复杂度:O(log(m+n))。
排序序列长度为 m+n,套用快速排序的空间复杂度即可,平均情况为 O(log(m+n))。
快速排序视频讲解
数据结构合集 - 快速排序(算法过程, 效率分析, 稳定性分析)_哔哩哔哩_bilibili
方法二:双指针
def merge(nums1, m, nums2, n): merged = [] # 创建临时列表 p1 = 0 p2 = 0 # 使用 and 而非 or,确保只有一个数组遍历完就停止 while p1 < m and p2 < n: if nums1[p1] < nums2[p2]: merged.append(nums1[p1]) p1 += 1 else: merged.append(nums2[p2]) p2 += 1 # 处理剩余元素(只会有一个数组有剩余) merged.extend(nums1[p1:m]) merged.extend(nums2[p2:n]) # 正确修改原始数组(使用切片赋值) nums1[:] = merged # 覆盖原始数组的内容# 示例nums1 = [1, 2, 3, 0, 0, 0]m = 3nums2 = [2, 5, 6]n = 3merge(nums1, m, nums2, n)print(nums1) # 输出: [1, 2, 2, 3, 5, 6]时间复杂度:O(m+n)每个元素最多被访问两次(一次添加到临时列表,一次复制回原数组)。
空间复杂度:O(m+n)需要临时列表存储合并结果。
方法三:逆双指针(最佳)
class Solution(object): def merge(self, nums1, m, nums2, n): p1=m-1 p2=n-1 tail=m+n-1 while p1>=0 or p2>=0: if p2==-1: nums1[tail]=nums1[p1] p1-=1 elif p1==-1: nums1[tail]=nums2[p2] p2-=1 elif nums1[p1]>nums2[p2]: nums1[tail]=nums1[p1] p1-=1 else: nums1[tail]=nums2[p2] p2-=1 tail-=1 时间复杂度:O(m+n)。
指针移动单调递减,最多移动 m+n 次,因此时间复杂度为 O(m+n)。
空间复杂度:O(1)。
直接对数组 nums 1原地修改,不需要额外空间。
27. 移除元素
需要注意使用remove,删除后n的值会变。
class Solution(object): def removeElement(self, nums, val): k=0 n=0 while n<len(nums): if nums[n]==val: nums.remove(nums[n]) else: k+=1 n+=1 时间复杂度是 O(n²),空间复杂度是 O(1)
改善:
使用双指针,删除太费时间,避免删除操作:不直接删除元素,而是将不等于 val 的元素移到数组前部,输出只要前部就行了。
class Solution(object): def removeElement(self, nums, val): k=0 i=0 for i in range(len(nums)): if nums[i]!=val: nums[k]=nums[i] k+=1 return k 一个快指针,从头到尾遍历,一个慢指针记录有效元素。
时间复杂度:O (n),只需遍历一次数组
空间复杂度:O (1),原地修改数组
26. 删除有序数组中的重复项
跟上题一样,也用双指针解决
class Solution(object): def removeDuplicates(self, nums): p=0 i=1 for i in range(len(nums)): if nums[i]!=nums[p]: p+=1 nums[p]=nums[i] i+=1 return p+1 80. 删除有序数组中的重复项 II
双指针
class Solution(object): def removeDuplicates(self, nums): i=2 p=2 n=len(nums) if n<=2: return n else: for i in range(2,n): if nums[i]!=nums[p-2]: nums[p]=nums[i] p+=1 return p时间复杂度:O(n),其中 n 是数组的长度。我们最多遍历该数组一次。
空间复杂度:O(1)。我们只需要常数的空间存储若干变量。
也可改用单指针
class Solution(object): def removeDuplicates(self, nums): p=0 for i in range(len(nums)): if p<2 or nums[i]!=nums[p-2]: nums[p]=nums[i] p+=1 return p169. 多数元素 - 力扣(LeetCode)
方法一:哈希表
class Solution(object): def majorityElement(self, nums): counts=collections.Counter(nums) return max(counts.keys(),key=counts.get)key 接收一个函数,用于指定每个元素的比较值。
collections.Counter(nums) 是 Python 中用于统计可迭代对象(如列表、字符串等)中元素出现次数的高效工具。它属于标准库 collections 模块,返回一个特殊的字典(Counter 对象),其中键为元素值,值为对应元素的出现次数。
方法二:摩尔投票算法(Boyer-Moore Voting Algorithm)
方法思路
摩尔投票算法的核心思想是通过抵消不同元素的计数,最终剩下的元素即为多数元素。具体步骤如下:
-
初始化候选人:将数组的第一个元素设为初始候选人。
-
计数器初始化:将计数器初始化为 1。
-
遍历数组:从第二个元素开始遍历数组:
-
如果当前元素与候选人相同,则计数器加 1。
-
如果当前元素与候选人不同,则计数器减 1。
-
当计数器减为 0 时,更换候选人为当前元素,并将计数器重置为 1。
-
-
返回结果:遍历结束后,候选人即为多数元素。
该算法的正确性在于,多数元素的出现次数超过一半,即使在最坏情况下,每次抵消操作后,多数元素仍会在剩余元素中占据多数,因此最终的候选人必定是多数元素。
class Solution(object): def majorityElement(self, nums): candidate = nums[0] count = 1 for num in nums[1:]: if num == candidate: count += 1 else: count -= 1 if count == 0: candidate = num count = 1 return candidate189. 轮转数组 - 力扣(LeetCode)
方法一:环状替换
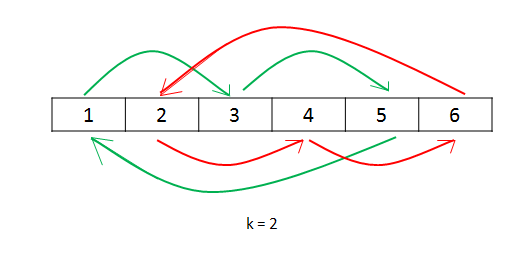
from math import gcdclass Solution: def rotate(self, nums, k): n=len(nums) k=k%n count=gcd(k,n) for start in range(count): current=start prev=nums[start] while True: next=(current+k)%n nums[next],prev=prev,nums[next] current=next if current==start: break方法二:数组翻转
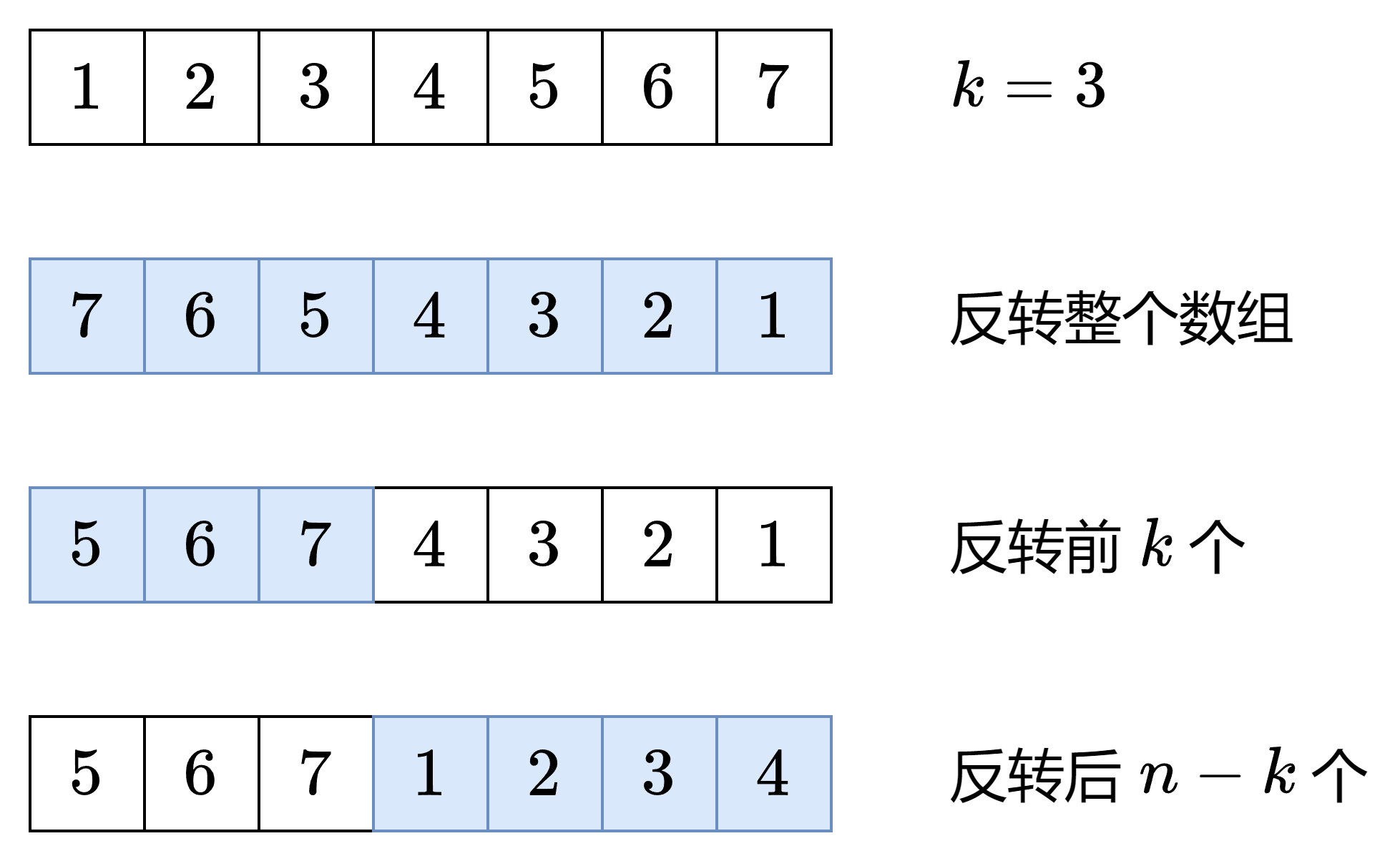
class Solution(object): def rotate(self, nums, k): def reverse(i:int,j:int)->None: while i<j: nums[i],nums[j]=nums[j],nums[i] i+=1 j-=1 n=len(nums) k%=n reverse(0,n-1) reverse(0,k-1) reverse(k,n-1)121. 买卖股票的最佳时机 - 力扣(LeetCode)
方法一:遍历
class Solution: def maxProfit(self, prices: List[int]) -> int: minprice = prices[0] maxprofit = 0 for price in prices: minprice = min(minprice,price) maxprofit = max(maxprofit,price - minprice) return maxprofit方法二:动态规划 (dp)
基本原理是将大问题分解为小问题,通过保存中间结果来避免重复计算,从而提高算法的效率。
class Solution: def maxProfit(self, prices: List[int]) -> int: n = len(prices) if n == 0: return 0 else: dp = [0] * n minprice = prices[0] for i in range(1,n): minprice = min(minprice,prices[i]) dp[i] = max(dp[i-1],prices[i] - minprice) return dp[-1] 122. 买卖股票的最佳时机 II - 力扣(LeetCode)
方法一: 动态规划(dp)
基本步骤:
1.定义状态:用变量描述问题在某一阶段的具体情况,明确子问题的解的表示方式。
2.确定状态转移方程:建立当前状态与前序状态之间的推导关系,明确如何从已知子问题的解推出当前问题的解。
3.初始化边界条件:设定最小子问题的解,作为状态转移的起点。
4.确定计算顺序:确保在计算当前状态时,其依赖的所有前序状态已被计算,可通过自底向上(迭代)或自顶向下(递归 + 记忆化)的方式进行。
class Solution: def maxProfit(self, prices: List[int]) -> int: n = len(prices) if n == 1: return 0 else: dp = [[0]*2 for j in range(n)] dp[0][0] = 0 dp[0][1] = -prices[0] for i in range(1,n): dp[i][0] = max(dp[i-1][0],dp[i-1][1] + prices[i]) dp[i][1] = max(dp[i-1][1],dp[i-1][0] - prices[i]) return dp[-1][0]方法二:贪心算法
贪心算法的核心思想是通过一系列局部最优选择来构建全局最优解。
思路是遍历价格数组,只要后一天的价格比前一天高,就将差值累加到总利润中。
class Solution: def maxProfit(self, prices: List[int]) -> int: maxprofit = 0 n = len(prices) if n == 1: return 0 else: for i in range(1,n): if prices[i] > prices[i-1]: maxprofit += prices[i] - prices[i-1] return maxprofit55. 跳跃游戏 - 力扣(LeetCode)
方法一:贪心算法
class Solution: def canJump(self, nums: List[int]) -> bool: max_reach = 0 for i in range(len(nums)): # 如果当前位置i超过了最远能到达的位置max_reach,说明无法到达i,返回False if i > max_reach: return False # 更新最远能到达的位置:取当前max_reach和i + nums[i]中的较大值 max_reach = max(max_reach,i + nums[i]) # 如果最远能到达的位置已经超过或等于数组的最后一个位置,返回True if max_reach >= len(nums) - 1: return True return False# 遍历结束仍未到达终点,返回False 方法二:从后往前贪心算法
class Solution: def canJump(self, nums: List[int]) -> bool: end = len(nums) - 1 for i in range(len(nums)-2,-1,-1): if i + nums[i] >= end: end = i return end == 0方法三:dp
class Solution: def canJump(self, nums: List[int]) -> bool: n = len(nums) if n == 0: return False dp = [False] * n dp[-1] = True # 从倒数第二个位置向前遍历 for i in range(n-2, -1, -1): # 检查从当前位置i能跳到的最远位置(不超过数组边界) max_jump = min(i + nums[i], n-1) # 检查所有可能的跳跃位置j(从i+1到max_jump) for j in range(i+1, max_jump+1): if dp[j]: # 如果j可达终点 dp[i] = True # 则i也可达终点 break # 只要找到一个可达的j,就无需继续检查 return dp[0] # 返回起点是否可达终点45. 跳跃游戏 II - 力扣(LeetCode)
方法一:从后往前贪心算法
思路:每一步都找到最左的起跳点,从而能够保证跳数最小
class Solution: def jump(self, nums: List[int]) -> int: m = len(nums) - 1 step = 0 while m > 0: for i in range(m): if i + nums[i] >= m: m = i step += 1 break return step时间复杂度:O(n^2),其中 n 是数组长度。有两层嵌套循环,在最坏的情况下,例如数组中的所有元素都是 1,position 需要遍历数组中的每个位置,对于 position 的每个值都有一次循环。
空间复杂度:O(1)。
方法二:从前往后贪心算法
class Solution: def jump(self, nums: List[int]) -> int: n = len(nums) maxPos,end,step = 0,0,0 for i in range(n - 1): if maxPos >= i:# 确保当前位置可达 maxPos = max(maxPos,i + nums[i]) if i == end: # 到达当前跳跃边界时 end = maxPos # 更新边界为最远可达位置 step += 1 return step 时间复杂度:O(n),在算法中,我们只需对数组进行一次遍历,其中n是数组的长度。在遍历过程中,每个元素的处理时间都是常数时间O(1),因此总的时间复杂度为O(n)。
空间复杂度:O(1)
三、小结
本博客代码参考官方题解和豆包,在leetcode中也有其他算法和设计思路可以参考学习,希望大家一起努力(*^▽^*)!
收获:双指针,正向和逆向,dp,贪心算法
PS:代码或解析有误之处,欢迎uu们评论或私信联系。


