从0开始机器学习--12.决策分析-运筹优化与数学建模（决策分析方法，评价模型-层次分析法AHP、灰色综合评价法/灰色关联法、模糊综合评价法、TOPSIS法、数据包络分析DEA、组合评价法，含代码）_ahp-topsis评价法

技术文档

写在前面

这些内容准确来说严格意义上不属于机器学习，把这部分内容归在这篇专栏中，主要原因之一是：机器学习算是与评价模型有关，且机器学习可以解决数学建模的问题。（其实就是我不想让这篇文章没有专栏归属，就把它聚类到这里了，后续若有更新其他运筹或数模的文章会再单独分类的~）

机器学习与评价模型的关系与联系

机器学习（Machine Learning） 主要通过数据驱动的方法来学习模型，用于从历史数据中发现模式并进行预测或决策。评价模型是用来对某个系统或过程进行量化和评估的工具，常常用来帮助决策。机器学习和评价模型在实际应用中有紧密的联系，特别是在多目标决策、优化和自动化评估中，机器学习算法常用于评估标准和模型参数的学习和改进。

《机器学习》：通过训练数据，构建预测模型，通常包含监督学习、无监督学习、强化学习等方法。
评价模型：帮助决策者分析不同选项的优劣，常用于多标准决策分析。
联系：评价模型为机器学习算法提供了评估准则，反过来，机器学习算法可优化决策模型的效果，使其更具智能化和自动化。
《决策分析》：
- 主要研究如何在不确定、模糊或复杂的环境下对决策问题进行分析和选择。这些评价模型（如AHP、TOPSIS、DEA等）正是该领域的核心方法。
- 决策分析关注的是如何通过数学和统计方法来支持决策过程，尤其是如何处理多准则决策和复杂的决策问题。
《运筹与优化》：
- 该领域主要研究如何通过数学模型、算法和计算方法来优化资源的配置、时间的安排等。运筹学通常更加关注约束条件下的最优化问题，如线性规划、整数规划、动态规划等。
- 如果涉及到优化决策问题（例如，利用优化算法来解决某些决策模型中的最优方案选择问题），那部分内容可能会涉及到运筹与优化。
《数学建模》：
- 数学建模是通过建立数学模型来描述现实问题，通常会结合数据、方程和算法来解决实际问题。数学建模的应用场景非常广泛，从经济学、工程学到管理学、医学等都有涉及。
- 在数学建模中，决策分析方法可以作为一个工具，用来建立多目标、多约束条件的决策模型，并求解最优解。

本专栏其他内容:

1.python基础；
2.ai模型概念+基础；
3.数据预处理；
4.机器学习模型--1.编码（嵌入）；2.聚类；3.降维；4.回归（预测）；5.分类；
5.正则化技术；
6.神经网络模型--1.概念+基础；2.几种常见的神经网络模型；
7.对回归、分类模型的评价方式；
8.简单强化学习概念；
9.几种常见的启发式算法及应用场景；
10.机器学习延申应用-数据分析相关内容--1.A/B Test；2.辛普森悖论；3.蒙特卡洛模拟；
11.数据挖掘--关联规则挖掘
12.数学建模--决策分析方法，评价模型
13.主动学习（半监督学习）
以及其他的与人工智能相关的学习经历，如数据挖掘、计算机视觉-OCR光学字符识别、大模型等。

合集链接https://blog.csdn.net/m0_73752612/category_12799244.html?fromshare=blogcolumn&sharetype=blogcolumn&sharerId=12799244&sharerefer=PC&sharesource=m0_73752612&sharefrom=from_link

写在前面

机器学习与评价模型的关系与联系

决策分析

基本概念与问题

决策分析方法

评价模型

层次分析法（AHP）

简单综述介绍

假设条件/超参数

思想/原理介绍（公式）

算法步骤

主要应用场景

优缺点

简单Python演示代码

灰色综合评价法（灰色关联法）

简单综述介绍

假设条件/超参数

思想/原理介绍（公式）

算法步骤

主要应用场景

优缺点

简单Python演示代码

模糊综合评价法

简单综述介绍

假设条件/超参数

思想/原理介绍（公式）

算法步骤

主要应用场景

优缺点

简单Python演示代码

TOPSIS法

简单综述介绍

假设条件/超参数

思想/原理介绍（公式）

算法步骤

主要应用场景

优缺点

简单Python演示代码

数据包络分析（DEA）

简单综述介绍

假设条件/超参数

思想/原理介绍（公式）

算法步骤

主要应用场景

优缺点

简单Python演示代码

组合评价法

简单综述介绍

假设条件/超参数

思想/原理介绍

算法步骤

主要应用场景

优缺点

总结

决策分析

基本概念与问题

决策分析 是指在面对不确定性和复杂情况时，使用科学的方式来选择最优决策方案的过程。其主要问题是如何在多种选择方案中做出最优决策，尤其是在不确定、风险和利益冲突的情况下。

决策分析与评价模型的关系与联系：

决策分析 提供了评估决策效果的框架，评价模型为决策分析提供了具体的评估工具。
决策分析在考虑决策目标和可行方案时，利用评价模型来衡量每个选项的优劣，为最终决策提供依据。

决策分析方法

风险型决策方法：

风险决策的期望值法：基于每个决策可能产生的结果及其发生概率计算期望值，选择期望值最大（或最小）的决策。
- 优点：量化风险，帮助决策者理性决策。
- 缺点：依赖于概率的准确性。
利用后验概率的方法及信息价值：根据追加信息对先验概率进行修正，并根据后验概率进行修正（类似于贝叶斯分类器的原理）（可见本专栏《4.4分类》）。将获取追加信息的费用与带来的收益增加值进行比较判断。
决策树方法

不确定型决策方法：

无法知道哪种自然状态将出现，且对出现概率也不确定。主要取决于决策者的素质和要求。

乐观准则（max-max）：选择最优的最好的结果，适用于对风险容忍度高的决策者。
- 优点：简单直接。
- 缺点：忽略了风险。
悲观准则（max-min）：选择最坏结果中的最优，即对最坏结果进行保守选择，适合风险厌恶的决策者。
- 优点：规避最坏情况。
- 缺点：可能错失更好的机会。
等可能准则（Laplace准则）：假设所有决策方案的概率相等，选择期望值最大的方案。
- 优点：简单，适用于没有明确概率信息时。
- 缺点：可能过于简化。
遗憾准则（min-max）：选择最小化遗憾（即错过最好结果的损失）的决策。
- 优点：适合避免因错误选择导致的后悔。
- 缺点：计算较为复杂。
效用函数方法：通过效用函数来度量各个决策的满足程度，选择效用最大的决策。
- 优点：可以将不同标准量化为统一的效用值。
- 缺点：需要设计合理的效用函数。

评价模型

通常用于多方案决策分析（Multi-Criteria Decision Making, MCDM）

场景：当需要在多个备选方案中做出选择时，评价模型帮助根据不同的标准（或属性）对这些方案进行综合评估。
典型问题：选址问题（选择最佳商铺位置）、旅游推荐（选择最佳旅行目的地）、供应链优化（选择最优供应商）。
常用方法：层次分析法（AHP）、模糊综合评价法、灰色关联分析、TOPSIS等。

风险评估与决策优化

场景：在金融、工程、保险等地方，评价模型被用来评估不同方案或行为的风险，帮助决策者做出最优选择。
典型问题：金融投资组合优化、保险定价、工程项目的风险分析。
常用方法：效用理论、期望效用模型、风险评估模型等。

模型选择与比较、预测模型性能评估（见本专栏《7.模型评估》）

层次分析法（AHP）

简单综述介绍

层次分析法（AHP）是一种多准则决策分析方法，用于处理多标准决策问题。它通过将复杂问题分解成多个层次，并通过对比各方案之间的相对重要性来进行评估。AHP广泛应用于评估和选择方案，在项目管理、资源分配、风险管理等地方都有广泛应用。

AHP的主要特点是通过建立递阶层次结构, 把人类的判断转化到若干因素两两之间重要度的比较上, 从而把难于量化的定性判断转化为可操作的重要度的比较上面。在许多情况下, 决策者可以直接使用AHP进行决策, 极大地提高了决策的有效性、可靠性和可行性, 但其本质是一种思维方式, 它把复杂问题分解成多个组成因素, 又将这些因素按支配关系分别形成递阶层次结构, 通过两两比较的方法确定决策方案相对重要度的总排序。整个过程体现了人类决策思维的基本特征，即分解、判断、综合，克服了其他方法回避决策者主观判断的缺点。

多个准则层，一层一层求解

（1）从上到下顺序地存在支配关系，并用直线段表示。除目标层外，每个元素至少杯上一层一个元素支配。除最后一层外，每个元素至少支配下一层次一个元素，上下层元素的联系比同一层次强, 以避免同一层次中不相邻元素存在支配关系;
（2）整个结构中, 层次数不受限制;
（3）最高层只有一个元素, 每一个元素所支配的元素一般不超过 9 个, 元素过多时可进一步分组；准则层只对应两个方案时，将其余的那个方案权重设为0。
该图来源

假设条件/超参数

假设每个方案的比较是可量化的。
需要专家对不同方案进行成对比较。
超参数：无明显的超参数，依赖于判断矩阵的一致性。

思想/原理介绍（公式）

需要用到线性代数基础知识。

构建判断矩阵：对于每一对准则 $C_i$ 和 $C_j$ ，我们用数字 $a_{ij}$ 来表示它们之间的重要性比例（例如，1表示两者同等重要，3表示 $C_i$ 比 $C_j$ 重要）。
判断矩阵的一致性检验：对于矩阵的每个元素 $a_{ij}$ ，需满足 $a_{ij}$ · $a_{ij}$ =1。
特征向量法：通过计算判断矩阵的特征向量来得到各准则的权重。
- 算数平均法求权重（对每一列归一化处理，再对每一行取平均）
- 几何平均法求权重
  - 第一步：将A的元素按照行相乘得到一个新的列向量
  - 第二步：将新的向量的每个分量开 n 次方
  - 第三步: 对该列向量进行归一化即可得到权重向量
- 特征值求权重（使用的最多）
  - 第一步：求出矩阵A的最大特征值以及其对应的特征向量
  - 第二步：对求出的特征向量进行归一化即可得到我们的权重

算法步骤

构建决策问题的层次结构。
构建判断矩阵，进行专家评估。
计算判断矩阵的特征向量，得出每一层的权重。
一致性检验，确保判断矩阵的一致性。
通过加权平均法得出最终决策结果。

主要应用场景

项目选择
资源分配
风险评估
供应商选择

优缺点

优点：简洁易懂，适用于多层次、多标准的决策分析。
缺点：判断矩阵可能受到专家主观偏差的影响，且当层次和标准增多时，计算复杂度增大。

简单Python演示代码

例子来源及详解

小明想去旅游，经查阅攻略，初步选择苏杭、北戴河和桂林三地作为目标景点。请确定评价指标、形成评价体系为小明同学选择最佳的方案。

评价目标：去哪个城市旅游
可选方案：苏杭、北戴河、桂林
评价指标：知网搜索“旅游目的地影响因素”，阅读相关文献并在写论文中加以引用，选择：景点景色、旅游花费、居住环境、饮食情况、交通便利程度五个指标
完成表格：在确定表格权重时，采用分而治之的思想。一次性考虑这5个指标，往往考虑不周，两个两个指标进行比较，最终根据两两比较的结果来推算出权重。即层次分析法的思想。

层次图：

import matplotlib.pyplot as pltimport networkx as nx# 设置中文字体和负号显示plt.rcParams[\'font.sans-serif\'] = [\'SimHei\']plt.rcParams[\'axes.unicode_minus\'] = False# 创建一个有向图G = nx.DiGraph()# 添加节点G.add_node(\"选择最佳旅游城市\", level=0)G.add_node(\"交通便利性\", level=1)G.add_node(\"景点吸引力\", level=1)G.add_node(\"住宿价格\", level=1)G.add_node(\"苏杭\", level=2)G.add_node(\"北戴河\", level=2)G.add_node(\"桂林\", level=2)# 添加边（即层次关系）G.add_edges_from([ (\"选择最佳旅游城市\", \"交通便利性\"), (\"选择最佳旅游城市\", \"景点吸引力\"), (\"选择最佳旅游城市\", \"住宿价格\"), (\"交通便利性\", \"苏杭\"), (\"交通便利性\", \"北戴河\"), (\"交通便利性\", \"桂林\"), (\"景点吸引力\", \"苏杭\"), (\"景点吸引力\", \"北戴河\"), (\"景点吸引力\", \"桂林\"), (\"住宿价格\", \"苏杭\"), (\"住宿价格\", \"北戴河\"), (\"住宿价格\", \"桂林\"),])# 计算节点的层次pos = { \"选择最佳旅游城市\": (0, 2), \"交通便利性\": (-1, 1), \"景点吸引力\": (0, 1), \"住宿价格\": (1, 1), \"苏杭\": (-1, 0), \"北戴河\": (0, 0), \"桂林\": (1, 0)}# 绘制图形plt.figure(figsize=(8, 6))nx.draw(G, pos, with_labels=True, node_size=3000, node_color=\'skyblue\', font_size=10, font_weight=\'bold\', arrows=True)plt.title(\"层次分析法（AHP）层次图\")plt.show()

import numpy as npimport pandas as pd# 定义判断矩阵A = np.array([ [1, 3, 5, 7, 9], # 景点景色 [1/3, 1, 3, 5, 7], # 旅游花费 [1/5, 1/3, 1, 3, 5], # 居住环境 [1/7, 1/5, 1/3, 1, 3], # 饮食情况 [1/9, 1/7, 1/5, 1/3, 1] # 交通便利程度])# 打印判断矩阵df_A = pd.DataFrame(A, columns=[\"景点景色\", \"旅游花费\", \"居住环境\", \"饮食情况\", \"交通便利程度\"],  index=[\"景点景色\", \"旅游花费\", \"居住环境\", \"饮食情况\", \"交通便利程度\"])print(\"判断矩阵：\\n\", df_A)from numpy.linalg import eig# 求解特征值和特征向量eigvals, eigvecs = eig(A)# 取最大特征值对应的特征向量max_eigval_index = np.argmax(eigvals)weights = eigvecs[:, max_eigval_index].real# 归一化处理权重weights = weights / sum(weights)print(\"各评价指标的权重：\", weights)# 计算一致性比率（CR）CI = (eigvals[max_eigval_index] - len(A)) / (len(A) - 1)RI = 1.12 # 规模为5时的随机一致性指标（RI值）CR = CI / RIprint(\"一致性比率：\", CR)if CR < 0.1: print(\"一致性通过\")else: print(\"一致性不通过\")# 方案评分数据scores = np.array([ [9, 6, 7, 8, 6], # 苏杭 [7, 8, 7, 6, 7], # 北戴河 [8, 7, 8, 7, 8] # 桂林])# 计算各方案的综合评分final_scores = np.dot(scores, weights)print(\"各方案的综合评分：\", final_scores)# 选择得分最高的方案best_option = [\"苏杭\", \"北戴河\", \"桂林\"][np.argmax(final_scores)]print(\"最佳旅游城市选择：\", best_option)import matplotlib.pyplot as pltimport seaborn as sns# 设置中文字体和负号显示plt.rcParams[\'font.sans-serif\'] = [\'SimHei\']plt.rcParams[\'axes.unicode_minus\'] = False# 可视化判断矩阵sns.heatmap(A, annot=True, cmap=\"Blues\", xticklabels=df_A.columns, yticklabels=df_A.index)plt.title(\"判断矩阵\")plt.show()# 可视化各方案的综合评分plt.bar([\"苏杭\", \"北戴河\", \"桂林\"], final_scores)plt.xlabel(\"方案\")plt.ylabel(\"综合评分\")plt.title(\"各方案综合评分\")plt.show()

判断矩阵： 景点景色 旅游花费 居住环境 饮食情况 交通便利程度景点景色 1.000000 3.000000 5.000000 7.000000 9.0旅游花费 0.333333 1.000000 3.000000 5.000000 7.0居住环境 0.200000 0.333333 1.000000 3.000000 5.0饮食情况 0.142857 0.200000 0.333333 1.000000 3.0交通便利程度 0.111111 0.142857 0.200000 0.333333 1.0各评价指标的权重： [0.51281281 0.26149906 0.12897642 0.06337653 0.03333518]一致性比率： (0.05300786863555966+0j)一致性通过各方案的综合评分： [7.79416792 7.19812253 7.67512442]最佳旅游城市选择： 苏杭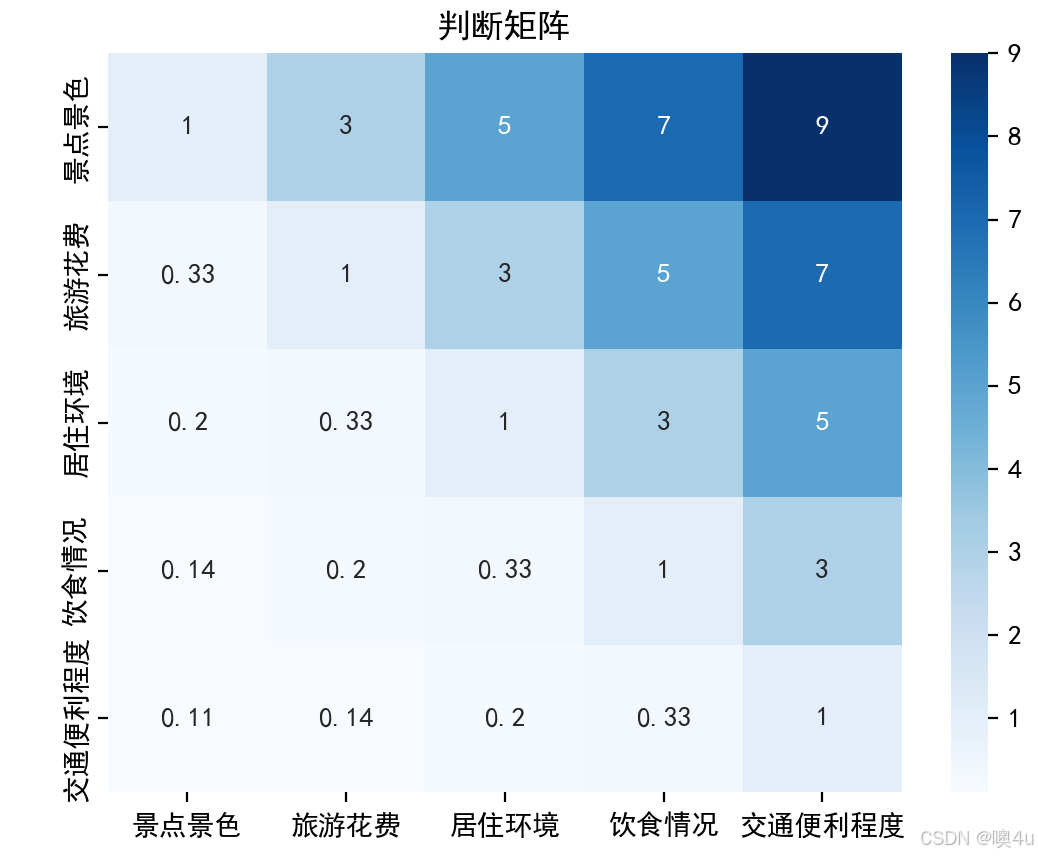

灰色综合评价法（灰色关联法）

简单综述介绍

灰色综合评价法基于灰色系统理论，主要用于处理系统中的不确定性信息。通过计算不同方案与理想方案之间的关联度来进行综合评估，广泛应用于环境监测、质量评价等地方。

灰色系统理论（Grey System Theory，GST）是一种用于分析和处理不确定性、部分信息不完全的系统理论。它的核心思想是：面对信息不完全、数据不完整、缺乏全知的情况，通过“灰色”而非“黑色”或“白色”的概念来进行建模和分析。灰色系统理论通过对系统中的不完全信息进行合理的推测和处理，以便揭示系统的规律，进而做出预测或决策。
主要步骤：
- 数据预处理：将原始数据进行归一化处理，使得各数据处于相同的标准。
- 计算关联度：通过计算各方案与理想方案的差异度，得到关联度。关联度越高，表示方案与理想方案越相似。
- 排序与评估：根据计算出的关联度对所有方案进行排序，选择最优方案。
主要方法：
- 灰色关联分析法（GRA）：用于分析和比较不同方案之间的优劣，广泛应用于工业质量评估、环境监测等地方。
- 灰色预测法：灰色系统中的灰色预测（GM）方法利用有限的历史数据来建立模型进行未来预测。灰色GM(1,1)模型是最常见的模型之一，广泛用于时间序列预测。
  - GM(1,1)模型的步骤：（具体见本专栏《4.3回归》）
    - 累加生成：通过对原始数据序列进行累加生成序列，以消除数据的波动性。
    - 建立灰色微分方程：根据累加序列建立一阶灰色微分方程，求解得到相关参数。
    - 预测：利用已建立的灰色模型进行未来值的预测。

假设条件/超参数

假设不同方案之间的数据能够进行灰色关联度分析。
超参数：无显式超参数。

思想/原理介绍（公式）

关联度计算公式： $\\xi_i = \\frac{min \\left( \\left| x_0 - x_i \\right| + \\rho \\right)}{max \\left( \\left| x_0 - x_i \\right| + \\rho \\right)}$ 其中， $x_0$ 为参考序列（理想方案）， $x_i$ 为待评估方案，ρ 为分辨系数（一般取 0.5 或 0.6）。关联度越高，代表越接近所谓的理想方案。

算法步骤

标准化原始数据。
计算每个方案与理想方案的灰色关联度。
根据关联度排序，得出评估结果。

主要应用场景

环境监测
工业质量控制
项目评价

优缺点

优点：能处理不完全和模糊的数据。
缺点：计算复杂，对数据的标准化要求较高。

简单Python演示代码

import numpy as npimport pandas as pdimport matplotlib.pyplot as plt# 设置中文字体和负号显示plt.rcParams[\'font.sans-serif\'] = [\'SimHei\']plt.rcParams[\'axes.unicode_minus\'] = False# 方案评分数据scores = np.array([ [9, 6, 7, 8, 6], # 苏杭 [7, 8, 7, 6, 7], # 北戴河 [8, 7, 8, 7, 8] # 桂林])# 归一化处理min_scores = np.min(scores, axis=0)max_scores = np.max(scores, axis=0)normalized_scores = (scores - min_scores) / (max_scores - min_scores)# 计算关联度ideal_solution = np.max(normalized_scores, axis=0) # 理想方案（最大值）disassociation = np.abs(normalized_scores - ideal_solution)min_disassociation = np.min(disassociation)max_disassociation = np.max(disassociation)# 灰色关联度grey_relations = (min_disassociation + 0.5 * max_disassociation) / (disassociation + 0.5 * max_disassociation)print(\"各方案的灰色关联度：\", grey_relations)# 计算每个方案的平均灰色关联度average_grey_relations = np.mean(grey_relations, axis=1)print(\"每个方案的平均灰色关联度：\", average_grey_relations)# 选择关联度平均值最大的方案best_option_gra = [\"苏杭\", \"北戴河\", \"桂林\"][np.argmax(average_grey_relations)]print(\"基于平均灰色关联度选择的最佳旅游城市：\", best_option_gra)# 可视化平均灰色关联度plt.bar([\"苏杭\", \"北戴河\", \"桂林\"], average_grey_relations)plt.xlabel(\"方案\")plt.ylabel(\"平均灰色关联度\")plt.title(\"每个方案的平均灰色关联度\")plt.show()

各方案的灰色关联度： [[1. 0.33333333 0.33333333 1. 0.33333333] [0.33333333 1. 0.33333333 0.33333333 0.5 ] [0.5 0.5 1. 0.5 1. ]]每个方案的平均灰色关联度： [0.6 0.5 0.7]基于平均灰色关联度选择的最佳旅游城市： 桂林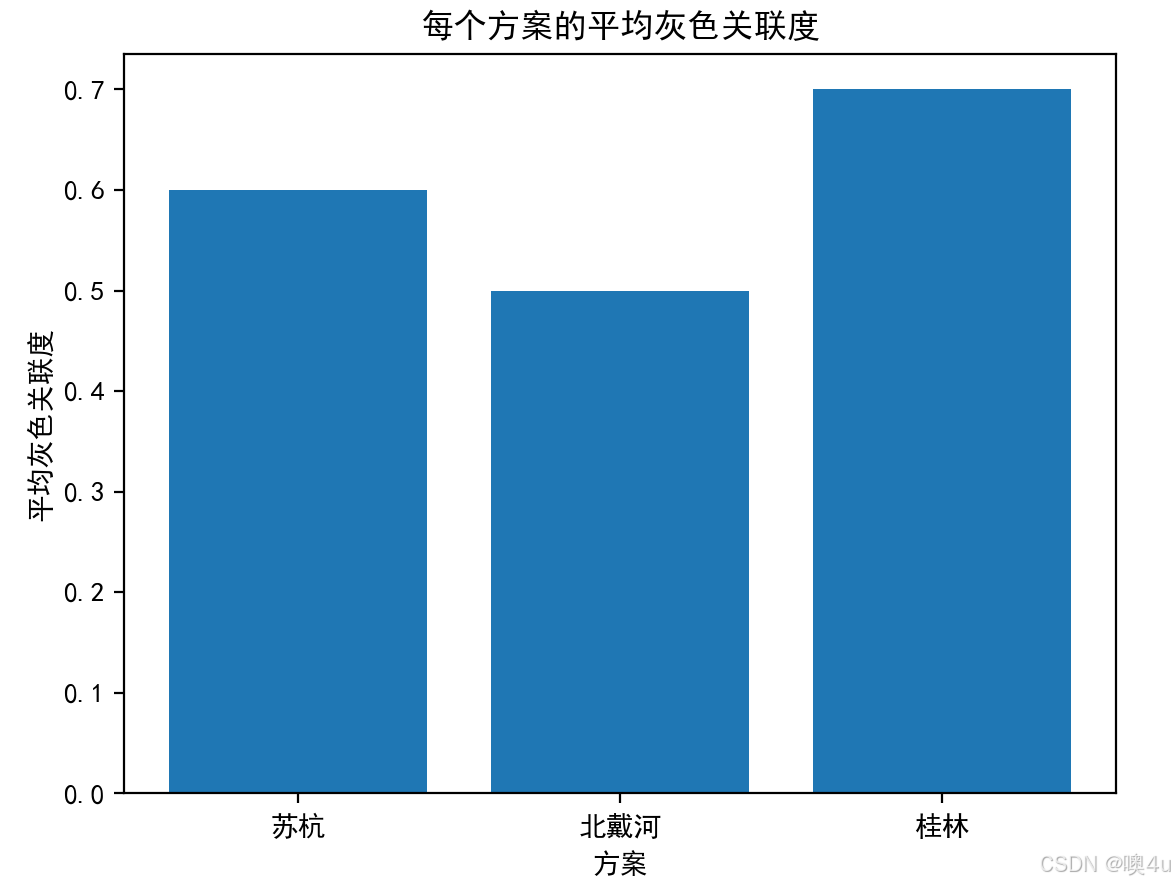

模糊综合评价法

简单综述介绍

模糊综合评价法基于模糊数学（若有需求的话可以单独出一篇博客介绍模糊数学、模糊控制等概念，可留言），旨在处理不确定和模糊性信息，通过隶属度函数对评价指标进行模糊化处理，最终综合得出各方案的评估结果。广泛应用于环境评估、健康评价等地方。

假设条件/超参数

假设评价数据能够进行模糊化处理。
超参数：隶属度函数的选择。

思想/原理介绍（公式）

隶属度函数：<img alt=\"\\mu(x) = \\frac{x - a}{b - a}, \\quad \\text{(a <= x 其中，a 和 b 为区间的上下界，x 为评价指标值，μ(x) 为隶属度。

算法步骤

确定评价指标。
为每个指标建立隶属度函数。
进行综合评估，得到综合得分。

主要应用场景

环境影响评价
社会安全评估
风险评估

优缺点

优点：能处理模糊、不确定性的信息。
缺点：需要专家经验（专家系统、PID专家控制）来构建隶属度函数。

简单Python演示代码

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom skfuzzy import control as ctrlimport skfuzzy as fuzz# 设置中文字体和负号显示plt.rcParams[\'font.sans-serif\'] = [\'SimHei\']plt.rcParams[\'axes.unicode_minus\'] = False# 方案评分数据scores = np.array([ [9, 6, 7, 8, 6], # 苏杭 [7, 8, 7, 6, 7], # 北戴河 [8, 7, 8, 7, 8] # 桂林])# 将评分归一化为0到1之间scores_fuzzy = scores / 10.0 # 评分归一化# 隶属度函数x = np.arange(0, 1.1, 0.1) # 隶属度函数的范围# 对每个评分设置隶属度函数（使用三角隶属度函数）fuzzy_scores = np.array([fuzz.trimf(x, [0, 0.5, 1]) for score in scores_fuzzy.flatten()])# 将每个方案的评分通过隶属度函数映射fuzzy_scores = fuzzy_scores.reshape(scores_fuzzy.shape[0], scores_fuzzy.shape[1], -1)# 权重weights_fuzzy = np.array([0.2, 0.3, 0.5]) # 假设每个评分的权重# 将权重调整为与 fuzzy_scores 相容的形状 (3, 1, 1)weights_fuzzy = weights_fuzzy[:, np.newaxis, np.newaxis] # 调整权重形状为 (3, 1, 1)# 计算每个评分项的加权隶属度评分weighted_scores = fuzzy_scores * weights_fuzzy# 对每个评分项求和，得到每个方案的综合评分fuzzy_composite_scores = np.sum(weighted_scores, axis=2).flatten()# 去除相同的评分值，保留唯一的评分fuzzy_composite_scores_unique = np.unique(fuzzy_composite_scores)# # 打印调试信息# print(\"模糊综合评分：\", fuzzy_composite_scores)# print(\"模糊综合评分的长度：\", len(fuzzy_composite_scores))# print(\"fuzzy_scores的形状：\", fuzzy_scores.shape)# print(\"fuzzy_scores的内容：\", fuzzy_scores)# 选择综合评分最高的方案best_option_fuzzy = [\"苏杭\", \"北戴河\", \"桂林\"][np.argmax(fuzzy_composite_scores_unique)]print(\"模糊综合评价法选择的最佳旅游城市：\", best_option_fuzzy)# 可视化模糊综合评价plt.bar([\"苏杭\", \"北戴河\", \"桂林\"], fuzzy_composite_scores_unique)plt.xlabel(\"方案\")plt.ylabel(\"模糊综合评分\")plt.title(\"模糊综合评分\")plt.show()

import numpy as npimport matplotlib.pyplot as plt# 构建一个简单的隶属度函数def membership_function(x, a, b): return (x - a) / (b - a)# 数据data = np.array([70, 80, 90, 85])a, b = 60, 100 # 隶属度函数区间# 计算隶属度membership_values = membership_function(data, a, b)# 可视化plt.bar(range(len(membership_values)), membership_values)plt.title(\"隶属度\")plt.xlabel(\"方案\")plt.ylabel(\"隶属度\")plt.show()

TOPSIS法

在本专栏《9.启发式算法》中对TOPSIS也有简单介绍。

简单综述介绍

TOPSIS（Technique for Order of Preference by Similarity to Ideal Solution）法通过计算各方案与理想解和负理想解的距离来进行排序，最终选择与理想解最接近的方案。常用于多目标决策问题。

假设条件/超参数

假设决策矩阵已经标准化。
超参数：无。

思想/原理介绍（公式）

正理想解：所有指标的最大值。
负理想解：所有指标的最小值。
计算每个方案与正负理想解的距离： $D_i^+ = \\sqrt{\\sum (X_i - X^+)^2} ; D_i^- = \\sqrt{\\sum (X_i - X^-)^2}$ 最终的接近度： $C_i = \\frac{D_i^-}{D_i^+ + D_i^-}$

算法步骤

构造决策矩阵。
标准化矩阵。
计算正负理想解。
计算与正负理想解的距离。
根据距离计算接近度，进行排序。

主要应用场景

项目优选
产品评估
资源分配

优缺点

优点：计算简单，结果清晰。
缺点：对权重敏感。

简单Python演示代码

import numpy as npimport pandas as pdfrom sklearn.preprocessing import MinMaxScalerimport matplotlib.pyplot as plt# 设置中文字体和负号显示plt.rcParams[\'font.sans-serif\'] = [\'SimHei\']plt.rcParams[\'axes.unicode_minus\'] = False# 构造决策矩阵decision_matrix = np.array([ [250, 60, 7], [300, 50, 8], [220, 70, 6]])# 标准化矩阵scaler = MinMaxScaler()norm_matrix = scaler.fit_transform(decision_matrix)# 计算正负理想解positive_ideal = np.max(norm_matrix, axis=0)negative_ideal = np.min(norm_matrix, axis=0)# 计算与理想解的距离dist_positive = np.sqrt(np.sum((norm_matrix - positive_ideal) ** 2, axis=1))dist_negative = np.sqrt(np.sum((norm_matrix - negative_ideal) ** 2, axis=1))# 计算接近度closeness = dist_negative / (dist_positive + dist_negative)# 可视化labels = [\'方案1\', \'方案2\', \'方案3\']plt.bar(labels, closeness)plt.ylabel(\'接近度\')plt.title(\'TOPSIS法评估结果\')plt.show()

数据包络分析（DEA）

简单综述介绍

数据包络分析（DEA）是一种评估多输入多输出决策单元（DMU）相对效率的方法，通过建立生产前沿来评估各单元的效率。广泛应用于银行、医院、教育等地方的效率评估。

假设条件/超参数

假设每个决策单元的输入输出可以量化。
超参数：无显式超参数。

思想/原理介绍（公式）

DEA的基本原理是通过线性规划来求解决策单元的相对效率。假设有 n 个决策单元，每个决策单元有 m 个输入和 s 个输出：

对于决策单元 j，它的相对效率满足以下线性规划：
- $\\text{Maximize} \\quad \\theta_j$
- subject to: $\\sum_{i=1}^n \\lambda_i x_{ij} \\leq \\theta_j y_{j}i=1$ λi≥0,i=1,2,…,n

算法步骤

构造决策单元的输入输出矩阵。
通过线性规划方法计算每个决策单元的效率。
得到每个单元的相对效率。

主要应用场景

企业效率评估
医院、银行等公共服务行业效率分析

优缺点

优点：无须考虑具体的权重，纯粹的效率评估。
缺点：对数据变化敏感，可能对某些数据偏差敏感。

简单Python演示代码

import numpy as npimport pandas as pdimport matplotlib.pyplot as plt# 设置中文字体和负号显示plt.rcParams[\'font.sans-serif\'] = [\'SimHei\']plt.rcParams[\'axes.unicode_minus\'] = False# 简单的DEA数据（输入，输出）inputs = np.array([ [200, 150], [400, 300], [300, 250]])outputs = np.array([ [100, 80], [200, 180], [150, 120]])# 计算相对效率（简化版）efficiencies = np.linalg.norm(outputs, axis=1) / np.linalg.norm(inputs, axis=1)# 可视化labels = [\'DMU1\', \'DMU2\', \'DMU3\']plt.bar(labels, efficiencies)plt.title(\"DEA效率评估\")plt.ylabel(\"效率\")plt.show()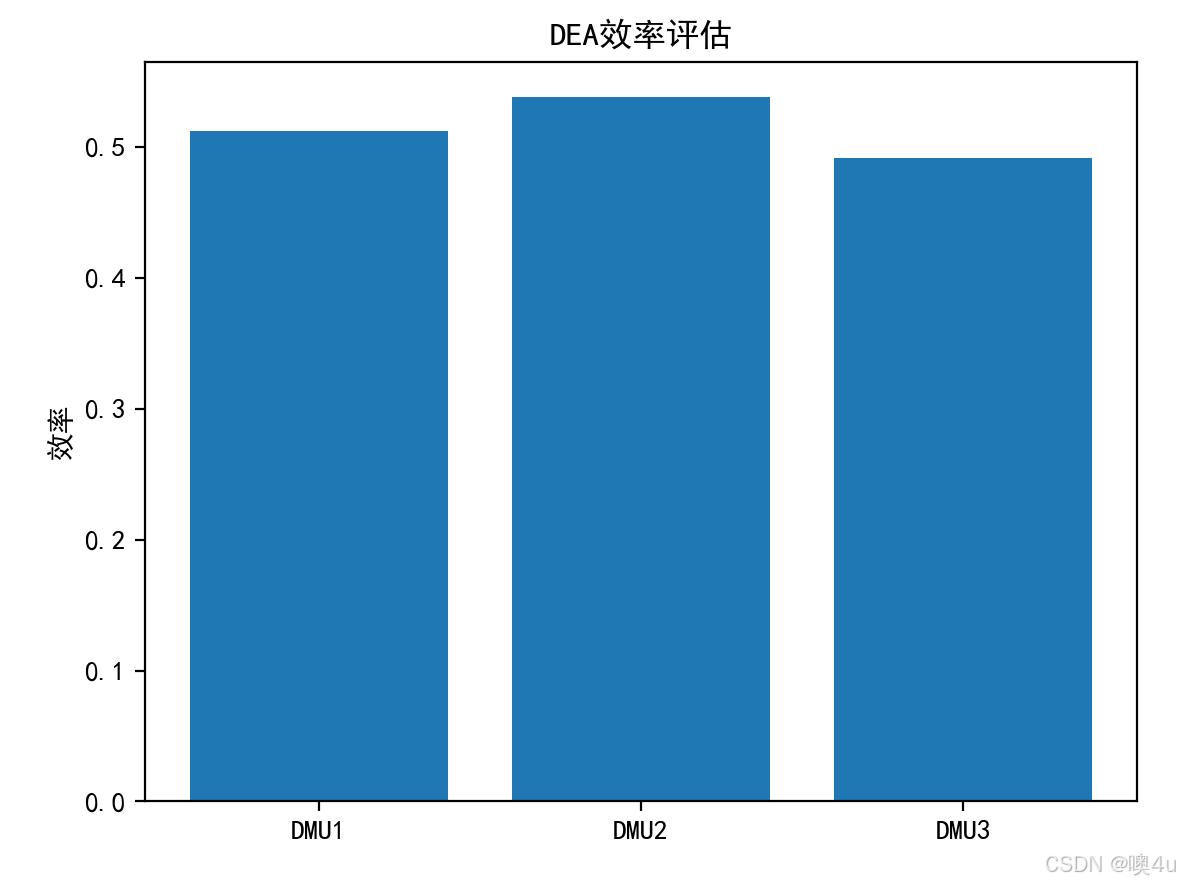

组合评价法

简单综述介绍

组合评价法通过结合多种评价方法来提高评估结果的准确性，弥补单一方法的不足。它利用多个模型的优点来得出最终的评价结果。

假设条件/超参数

假设选择的评价方法能够互补。
超参数：组合方法的权重和规则。

思想/原理介绍

通过加权平均或其他规则将多个评价方法的结果组合在一起，以便得到一个更为准确的评估结果。

算法步骤

选择多个评价方法。
对每个方法计算得分。
根据预设规则或权重进行组合。
得到最终的评估结果。

主要应用场景

复杂多目标决策问题。
需要多个角度进行评估的场景。

优缺点

优点：能够结合不同方法的优点，提高评估精度。
缺点：需要合理设计组合规则和权重，可能会复杂化计算过程。

总结

机器学习（ML）是通过数据学习模型以进行预测或决策，包含监督学习、无监督学习和强化学习等方法。评价模型用于多目标决策分析，帮助决策者量化和比较不同选项的优劣。机器学习与评价模型在实际应用中相辅相成，前者提供数据驱动的决策支持，后者则为机器学习模型提供评估标准和改进路径。决策分析主要处理多标准决策问题，运用数学和统计方法对复杂环境中的决策进行优化。常见的评价模型方法包括AHP、TOPSIS和灰色关联法等，这些方法通过对比和综合评价不同方案，帮助决策者在不确定性或风险条件下做出最优选择。此外，风险评估和决策优化在金融、工程等地方也有广泛应用，能够进一步提升决策的智能化与自动化。

从0开始机器学习--12.决策分析-运筹优化与数学建模（决策分析方法，评价模型-层次分析法AHP、灰色综合评价法/灰色关联法、模糊综合评价法、TOPSIS法、数据包络分析DEA、组合评价法，含代码）_ahp-topsis评价法

写在前面

机器学习与评价模型的关系与联系

决策分析

基本概念与问题

决策分析方法

评价模型

层次分析法（AHP）

简单综述介绍

假设条件/超参数

思想/原理介绍（公式）

算法步骤

主要应用场景

优缺点

简单Python演示代码

灰色综合评价法（灰色关联法）

简单综述介绍

假设条件/超参数

思想/原理介绍（公式）

算法步骤

主要应用场景

优缺点

简单Python演示代码

模糊综合评价法

简单综述介绍

假设条件/超参数

思想/原理介绍（公式）

算法步骤

主要应用场景

优缺点

简单Python演示代码

TOPSIS法

简单综述介绍

假设条件/超参数

思想/原理介绍（公式）

算法步骤

主要应用场景

优缺点

简单Python演示代码

数据包络分析（DEA）

简单综述介绍

假设条件/超参数

思想/原理介绍（公式）

算法步骤

主要应用场景

优缺点

简单Python演示代码

组合评价法

简单综述介绍

假设条件/超参数

思想/原理介绍

算法步骤

主要应用场景

优缺点

总结

相关问题

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载