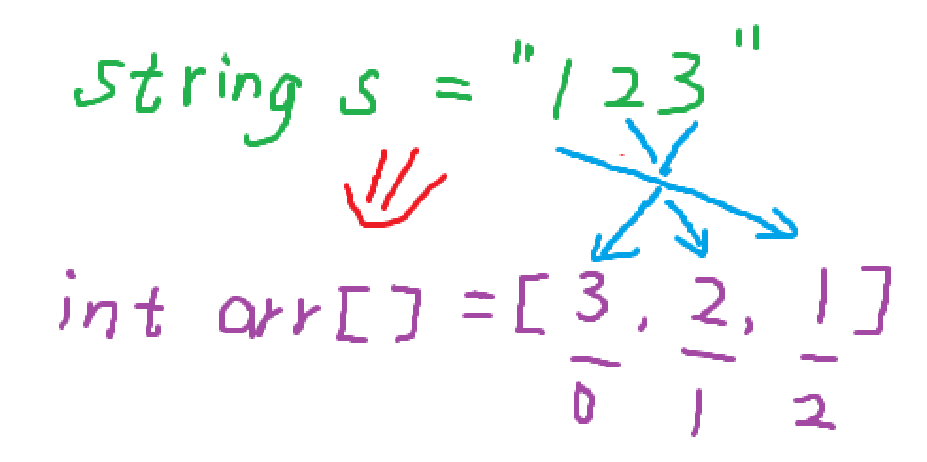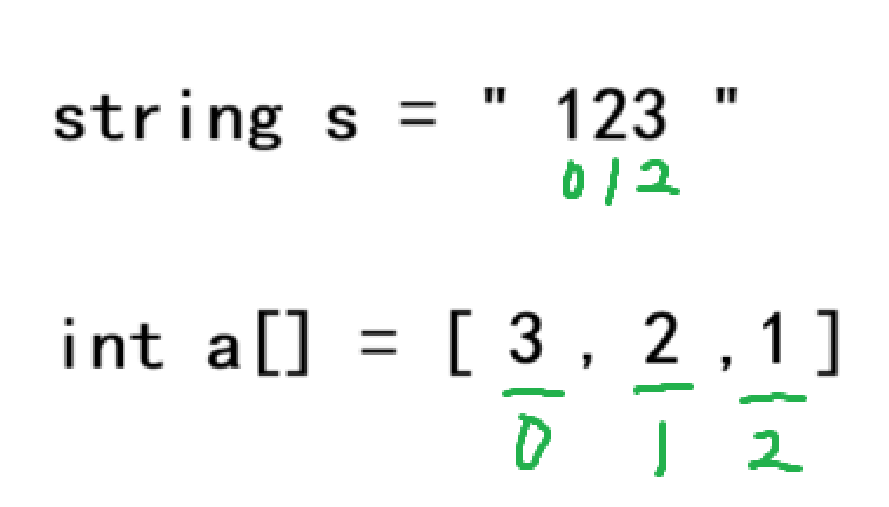【算法】高精度加、减、乘、除法_高精度加法
目录
引入
1.高精度算法概念
1.1什么是高精度?
1.2如何使用高精度来进行计算
1.3如何进行逆序存放
2.高精度算法的原理及其实现
2.1高精度加法
2.2高精度减法
2.3高精度乘法
2.4高精度除法
小结
引入
在算法领域里,高精度的计算也是属于其中的一部分,主要分为加法、减法、乘法、除法。接下来来带领大家深度了解一下算法——高精度算法的使用。
1.高精度算法概念
1.1什么是高精度?
举个例子,假如要使用1×10^5的数,那么可以使用int类型来存储这个数据,当然如果是1×10^18,longlong类型也足以存下。但假如说我要使用1×10^10000000或者是比这个更大的数呢,无论是int还是longlong,甚至是连最大的double都存储不下,那么这个数就被称为高精度数。
所以我们可以得出一个结论:当一个数据的特别大,甚至已经用各种类型都存储不下了(超出了类型范围),我们称这样的数据为大整数(也就是高精度数)。那么使用两个高精度数来进行计算方法我们也称为高精度算法(High Accuracy Algorithm)。
1.2如何使用高精度来进行计算
要运用高精度数来进行计算,首先得读入高精度数,可以先通过字符串(string)来将高精度数存储到字符串里面,因为计算机读入的数据是以字符的形式读入的。
例如数字“12345”,从我们的视角来看,是一串数字,但在计算机视角里,则是从左到右依次读入的五个字符:‘1’,‘2’,’3‘,’4‘,‘5’。
所以可以借助这样的一个特性,将特别庞大的高精度数存入到string字符串中,那么计算机就会将这一串数字当作字符串来存储(读入)下来。就算高精度的数字特别庞大,那么存入到字符串中,也就变成了一个长度很长的一个字符串罢了。比如一个数的数据范围是10的一万次方到10的十万次方之间,将它存放到字符串里, 这个字符串的长度撑死就是这个数的10的一万次方到10的十万次方的长度。所以在计算机视角,无论这个数的数据有多大多长,都可以把它当作一个字符串来读进来。
将高精度数读入进计算机后,那么下一步可以使用数组逆序存储这个数的每一位这一种形式。
字符串数据逆序存入数组形式图
为什么要使用数组逆序来存储这个数的每一位呢?因为在计算加减法的时候,都是从个位开始进行计算的然后再依次从十位百位逐渐往上进行运算。那我们将这个数逆序存入数组中时,对应的下标也就是从个位开始依次向后,在进行数组遍历的时候,就是从下标为0(个位)开始,跟我们的计算过程是一一对应的,也就是说从我们在进行模拟加法计算的结果也是从最低位到最高位。
还有一种情况是当处理进位的情况时,可以更好的处理进位数,如果是将字符串里的数正序存入数组,处理进位数则比较不方便。
将数存完之后,就可以利用数组来进行模拟加减乘除法运算了。
1.3如何进行逆序存放
其实并没有想象的很难,就是一个找规律的过程。
假定用字符串s读入了一个数“123”,接下来就要拆分存放到数组a中去。我们先把字符串和数组的下标写出来,此时字符串“1,2,3”各自对应的下标分别是“0,1,2”,数组的下标也标记出来。因为我们的最终目的是逆序存放到数组,所以在图例就先将数字存放到数组里面。
根据图例可以看出,字符串和数组的下标是有对应关系的,字符串中”1“的下标加上数组中”1“的下标是等于2,同理2和3也是一样。此时我们发现,两个下标相加的结果正好是对应字符串中长度再减1。因此当我们用一个i变量来对字符串进行从前往后的遍历时,所对应在数组中的下标位置就是ls(设置一个长度变量)减1再减i,我们要保证两个下标之和是等于字符串长度减一的。
还有个注意事项,我们在字符串里遍历得到的数据s[i]是字符,是要减去一个字符’0‘才能得到字符对应的数的。
搞清楚了原理,接下来就可以代码实现了。
#includeusing namespace std;const int N = 1e6 + 10;//定义一个N的范围(可根据需求修改)int a[N];//定义个数组来接收字符串的数int la;//定义一个变量来代表字符串的长度int main(){//定义个字符串来存入数据string s;cin >> s;la = s.size();//算出字符串s的长度赋值给变量la//拆分每一位,逆序存放在数组for (int i = 0; i < la; i++){a[la - 1 - i] = s[i] - \'0\';//i位置的字符在数组中的位置是字符串的长度减去1再减去i//确保i加上长度减1再减i的结果是长度减1}for (int i = 0;i < la;i++){cout << a[i] << \" \";//输出数组a的数}return 0;}输出的结果

2.高精度算法的原理及其实现
在运用两个数来进行加减乘除的时候可以使用小学列数式来进行,所以高精度算法本质就是用代码来模拟小学列竖式计算加减乘除的过程。
2.1高精度加法
进行高精度加法可以分成两步:1.读入字符串、拆分逆序存放到数组;2.利用数组来模拟小学列竖式计算加法的过程。第一步在前面已经讲解过了,现在就来进行第二步的操作。
咱们先来使用一下小学时学的列竖式来模拟一下计算。
首先先从最低位开始进行,计算一下4+7,得出来的结果为11,大于10则需要进1,进1则可以通过/10来将十位1传给前一位,将得出的结果%10留下余数,那么个位就完成了加法计算。后面的十位百位等等往上的位数都是如此。
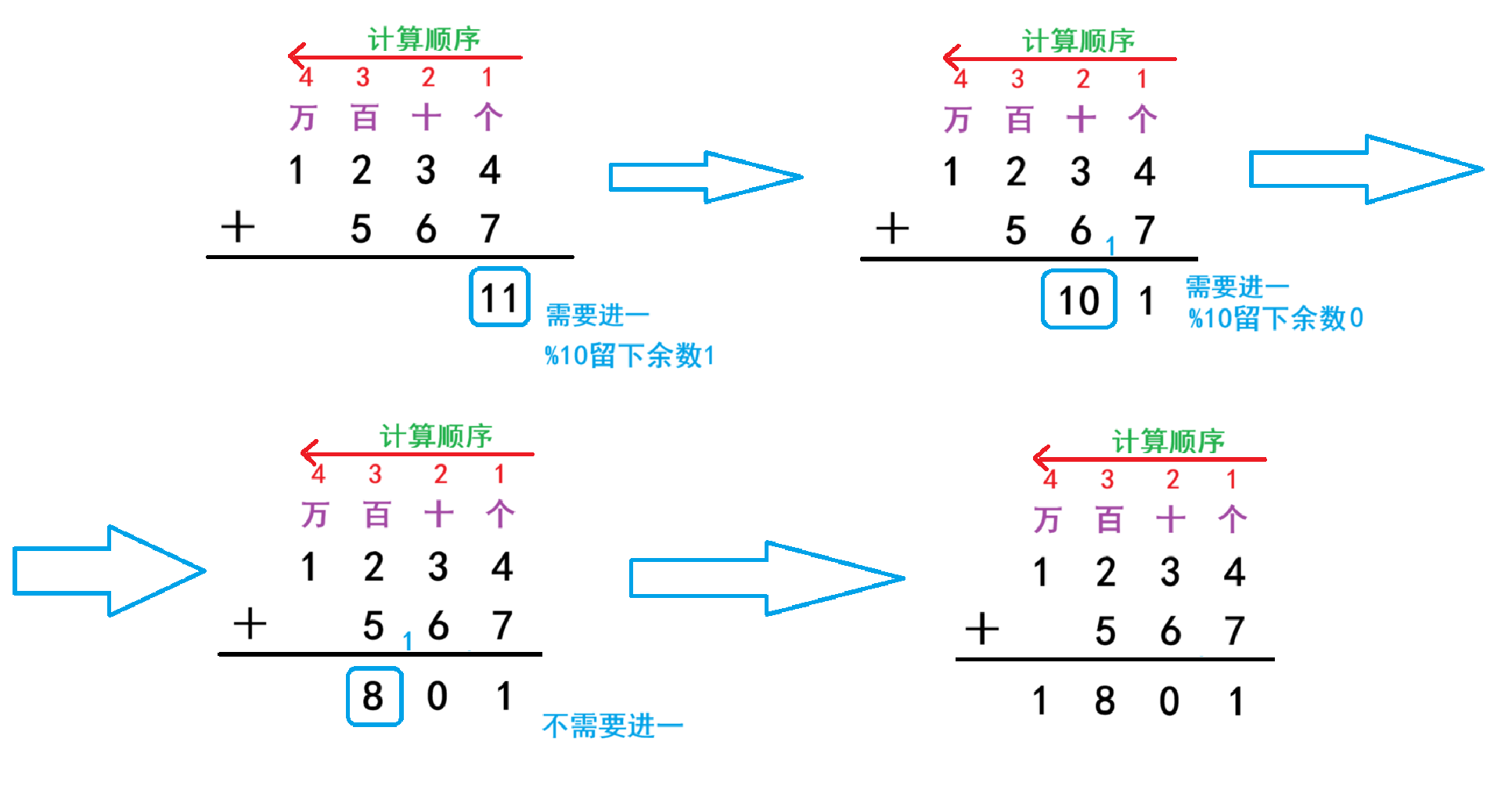
如果是要计算a +(-b)的话,我们可以同等于a - |b|,直接运用高精度减法即可。
那么由上面的例子,我们可以得出这样的规律:
- 对应位相加,然后再加上进位
- 处理进位
- 处理余数
刚刚的加法计算过程的每一个过程都是这三步循环,简单概述就是对应位先相加算出结果x,如果x>10则需要进位,因为我们最终看进位是看它的十位,那么进位就通过x/10得出十位数1,最后将进完位后的x%10得出余数留下来就是这个位数的计算结果。如果两数相加不需要进位,则可以直接将结果保留下来。
经过了的列竖式的模拟,接下来的数组计算也是和上面的差不多。
先建立分别建立三个数组来分别来逆序存放两个字符串的数据和计算出来的结果的数。这次来换一组数据来进行计算:1234+582。先计算下标为0的数字:2 + 4 = 6,然后处理进位,将6 / 10 = 0,算出的结果是进0,我们就在下一位放上我们的进位数0,接着处理余数:6 % 10 = 6,那么6就是我们的最终计算结果。
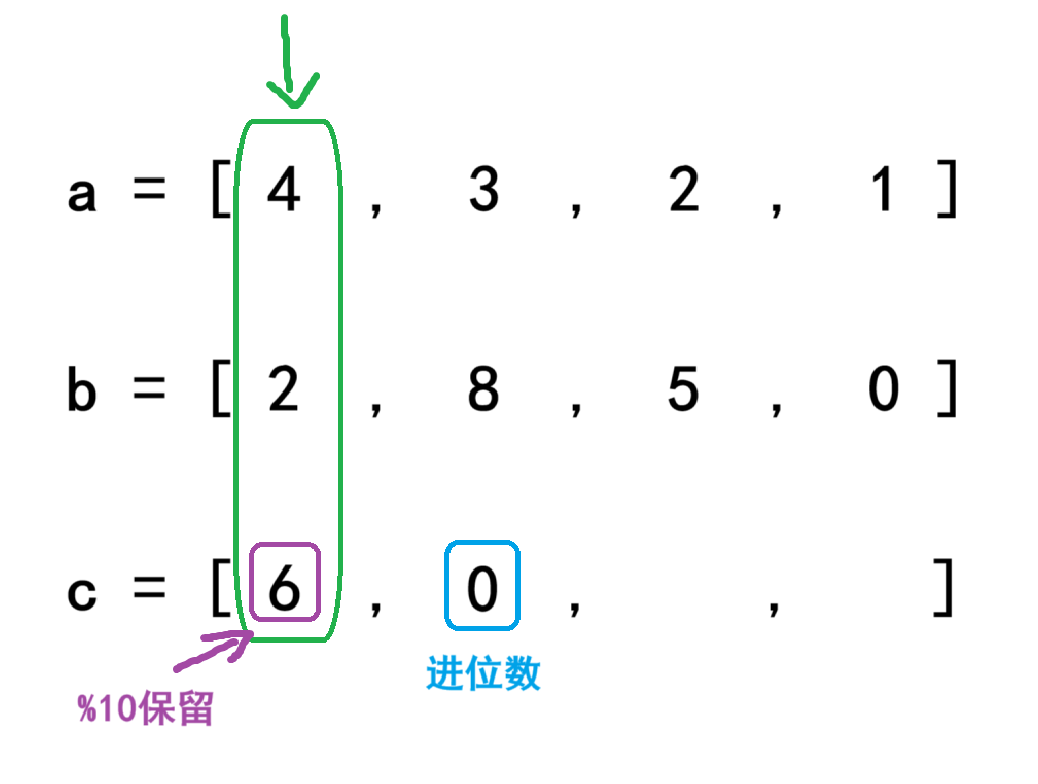
然后进行下一位的计算,首先进行对应位相加,然后再加上进位:3 + 8 + 0 = 11,然后处理进位:11 / 10 = 1,将进位数存入到下一位,最后处理余数:11 % 10 = 1,将最终结果1存放到原位置。
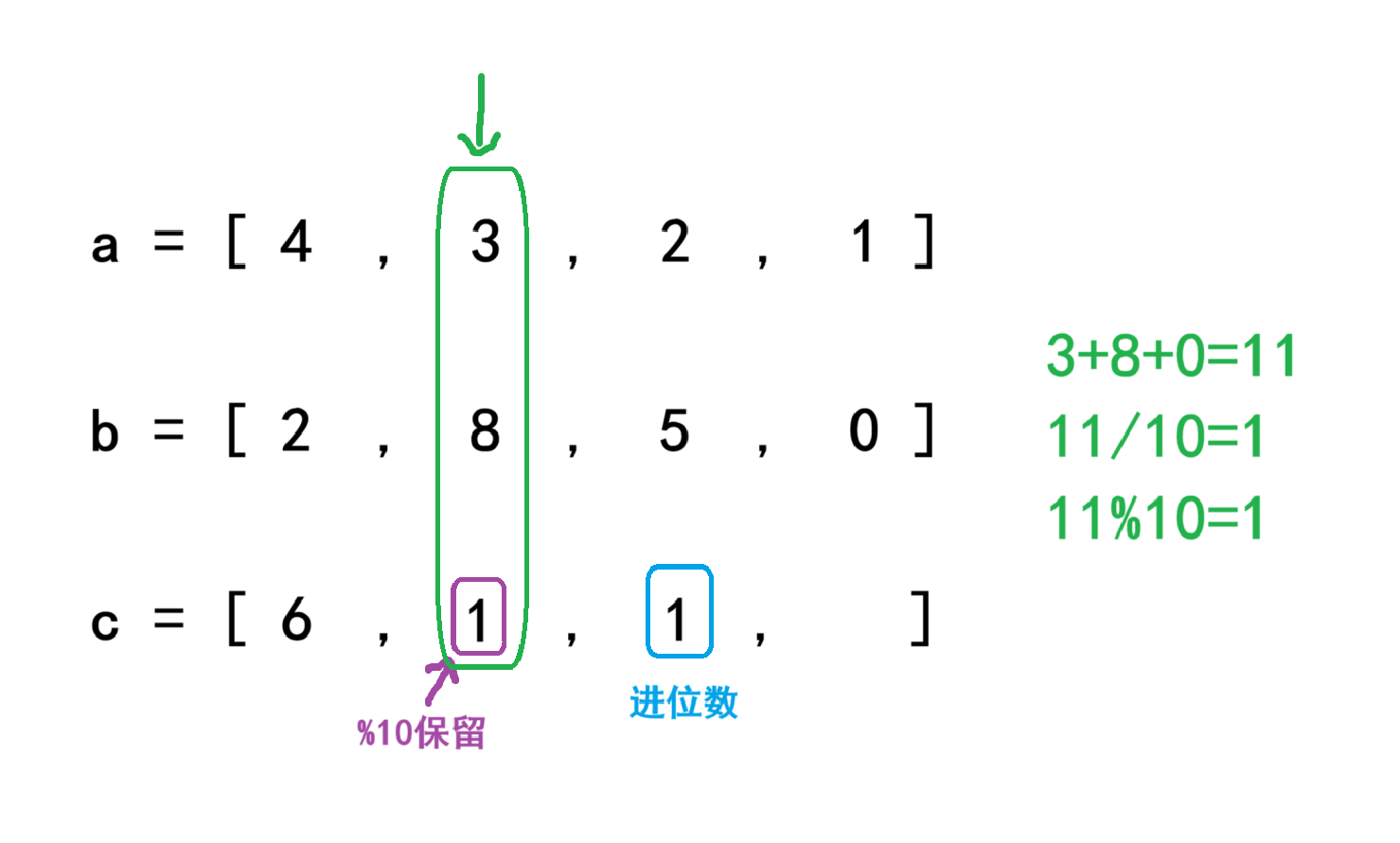
百位千位的计算方式也是一样的,最终算出来的结果就是c = [ 6 , 1 ,8 , 1 ],最后我们从后往前输出数组里的数就是我们的最终的计算结果了。

以上就是高精度加法的模拟实现,我们就可以通过上面形式来进行代码书写了。
//高精度加法#includeusing namespace std;const int N = 1e6 + 10;//设置数组初始长度(按自己情况进行设置)int a[N], b[N], c[N];//存放的数据 int la, lb, lc;//分别标记三个数组的长度void add(int c[], int a[], int b[]){for (int i = 0;i > x >> y;//分别计算两个字符串的长度la = x.size();lb = y.size();lc = max(la, lb);//结果数组中的长度是两者之间的最大值//第一步:拆分每一位,逆序存放到数组中for (int i = 0; i < la; i++){a[la - 1 - i] = x[i] - \'0\';}for (int i = 0; i = 0;i--){cout << c[i];}return 0;}运行结果

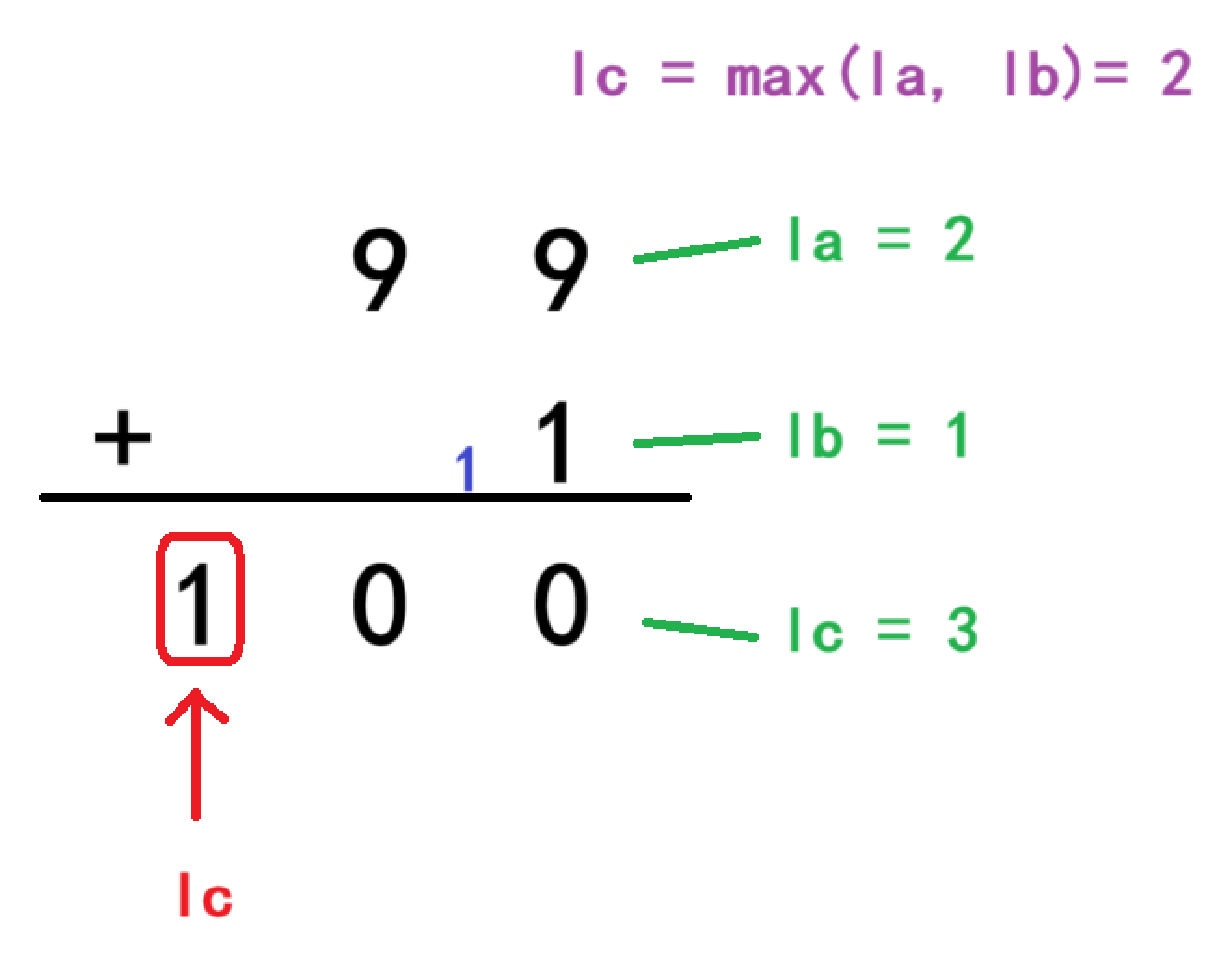
这里讲解一下边界问题,假如要进行99 + 1的加法时,得出的结果是100,也就是实际lc长度是3,但在进行计算前我们用lc = max(la, lb)计算的长度是2,所以输出的话则是只输出十位和个位的0。
这种情况lc的位置是还有数据的,所以为了防止最高位数据遗忘这种特殊情况,我们要进行判断。在正常计算循环后,如果c[lc]位置还有数据,就让lc++即可。
2.2高精度减法
高精度减法在加法中除了主要两个步骤相等的情况下,我们还要考虑减数和被减数的关系。
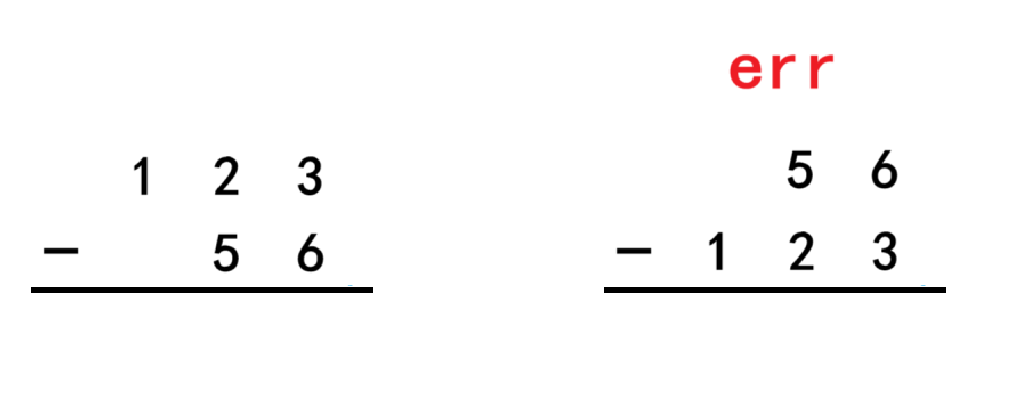
在正常的小学列竖式计算的中,我们是用较大的数当作被减数,较小的当作减数,如果相反来计算的话是错误的计算。假如遇到了要使用较小的数来减去较大的数的时候,就要将二者调换过来进行计算,最后在输出结果之前先输出一个负号(‘-’)就行。所以我们要在进行减法运算前先进行比较两个数的大小,然后用较大的数减去较小的数。在之前我们存储数据是用字符串来进行存储的,如果直接使用字符串来进行比较大小是会出错的,因为字符串是通过字典序的方式来进行比较的。

我们正常比较两个数的大小是看这个数的长度来进行比较的,但是字符串则是不管字符串的长度有多长,只比较两个字符串的最高位,谁的最高位大,那么谁的字符串就大。所以我们直接拿字符串来比较两个数的大小是错误的。我们的目的是比较字符串里面的数而不是字符串,所以就会导致计算数值的错误。处理这种情况的方法就是先比较两个数之间的长度,长度较长的数一定是大的,如果两个数的长度相等,那么就再按照字典序来比较两个数就可以了。
注意:我们这种比较方式只适用于比较字符串里面数的大小,如果是正常比较字符串的大小那么之间按照字典序来比较即可。
处理完大小的问题,接下来我们模拟一下减法的运算过程。以123减56为例,一样是从最低位开始计算。先用3减6等于-3,但最终在个位的结果是不能出现负数的,所以要向前借位1,也就是借了个10,我们直接用10来加上刚刚算出来的结果,就是这一位的最终结果。正常我们计算是3减6不够借1后13减6等于7,二者其实是一样的。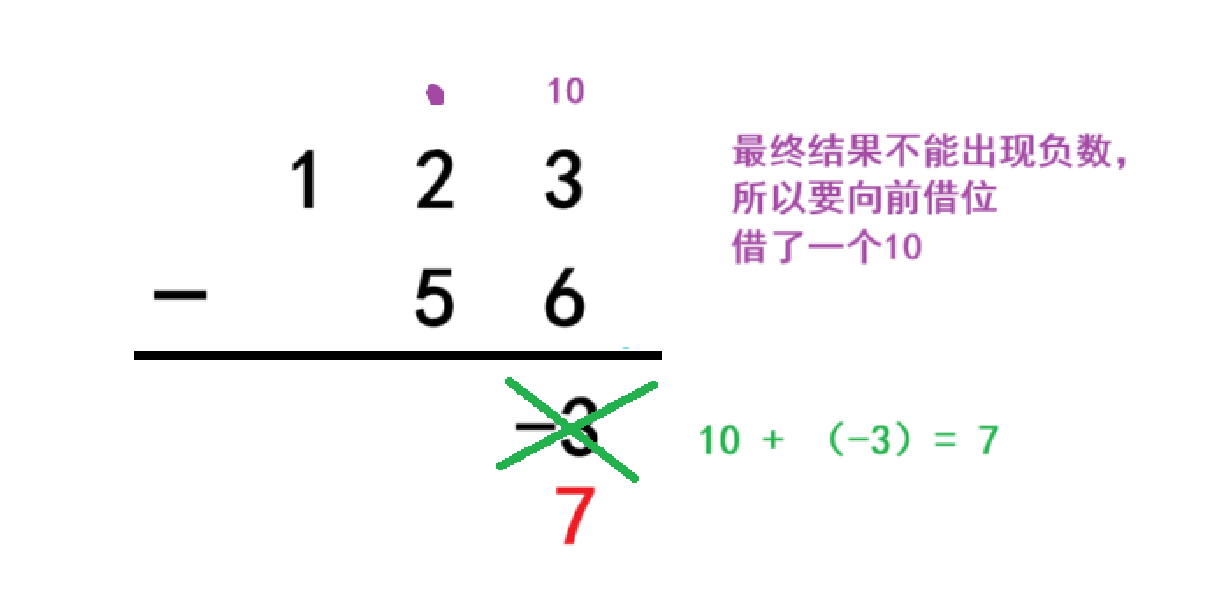
在十位借1后,十位的2就要减1变成1,而后再拿1直接减去5等于-4,最终结果不能是负数于是还要向前借1,用借来的10再加上-4等于6就是最终的结果了。计算完后百位的1被刚刚借位后要减1变成0,0加0等于0直接保留,这样整体计算就结束了。
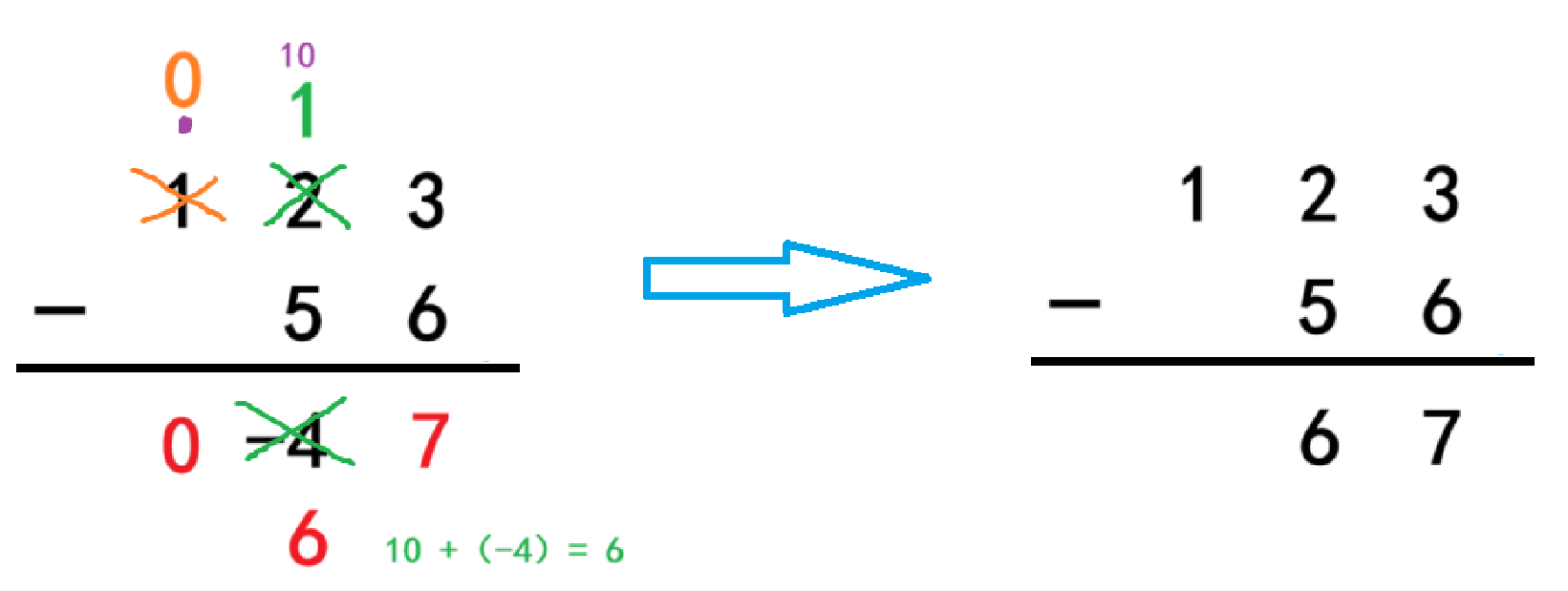
经过上面模拟可以得出一个规律:
1.先是对应位相减,然后处理借位
2.如果减的结果小于0,往前借一位,然后这一位加上10
数组的模拟也是和高精度加法是相似的,这里就不再进行模拟演示了,直接上代码书写。
//高精度减法#include using namespace std;const int N =1e6 + 10;int a[N],b[N],c[N];int la,lb,lc;bool cmp(string& x,string& y){//先比较长度 if(x.size() != y.size()){return x.size() < y.size();}//如果长度一样则比较字典序 return x < y; }void sub(int c[],int a[],int b[]){for(int i = 0;i <lc;i++){c[i] += a[i] -b[i];//对应位相减,然后处理借位if(c[i]<0)//如果算出的结果 1 && c[lc - 1] == 0){lc--;}}int main(){//建立两个字符串来输入要计算的高精度数string x,y;cin >> x >> y;//先建立一个函数cmp来比较大小,目的是判断是否是小数减大数if(cmp(x,y)) //如果函数返回的是true的话,那么计算的数是x<y{swap(x,y);//把两个数交换一下就是大数减小数了cout << \'-\';//在结果前面先输出个负号}la=x.size();lb=y.size();lc=max(la,lb);//拆分逆序存放for(int i = 0;i < la;i++){a[la-i-1] = x[i] - \'0\';}for(int i = 0;i = 0;i--){cout << c[i];}return 0;}运行结果

这里讲解一下前导零的问题,假如出现了999减998这种情况,此时lc的长度是为3,算出的结果是001,但实际输出是要删去前面的0只保留1,所以lc长度也要只减到1。还要一种情况是999减999,计算出的结果是为000,但不能将所有的0都删去,至少要保留一个0来输出。
所以要进行删去前导零但lc长度还要大于1,就得出了结论最终结果要大于1并且从c[lc - 1]是为0的时候,lc长度要减1。
2.3高精度乘法
高精度乘法和高精度加法的过程步骤是一样的,但在进行数组模拟的时候还是有些许不同的。咱们直接来模拟一下计算的过程。
咱们用123乘456来为例,正常的计算是从第二个乘数个位开始依次向第一个乘数相乘,接着到下一位,知道将所有位数全部乘完后,再各列进行相加,有进位的进位,最终就得出了结果。
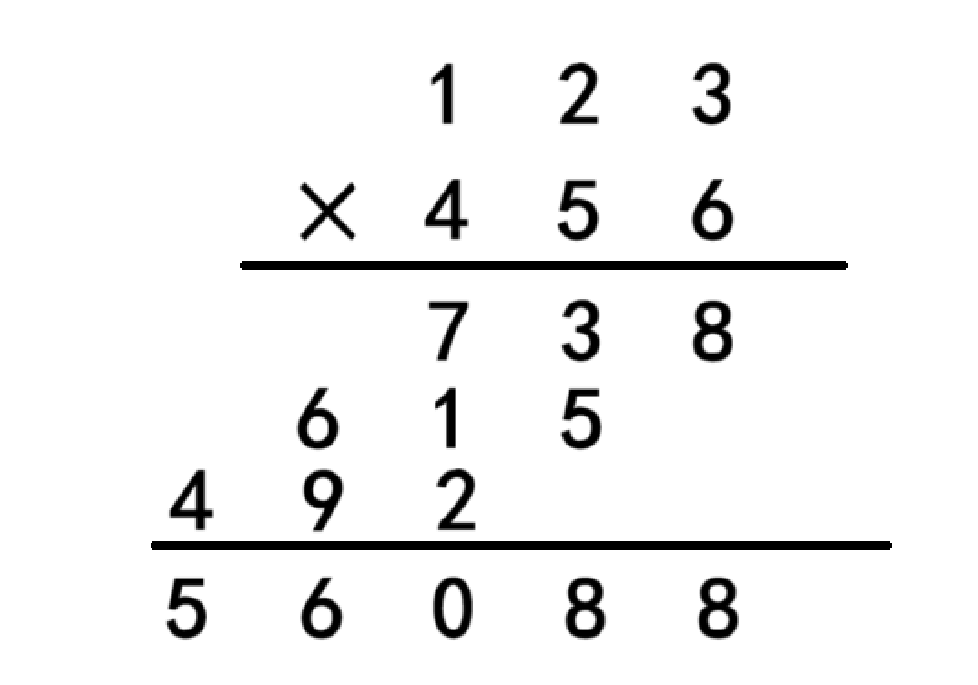
在这里有个点就是在3乘6的算出的结果为18时,我们要处理余数后还要进位,那么下一步2乘6等于12时还得进行加上进位以及又要处理进位和余数,这类过程比较繁琐。那么接下来有一个比较简单方便的方法,就是无进位相乘,然后相加,最后处理进位。
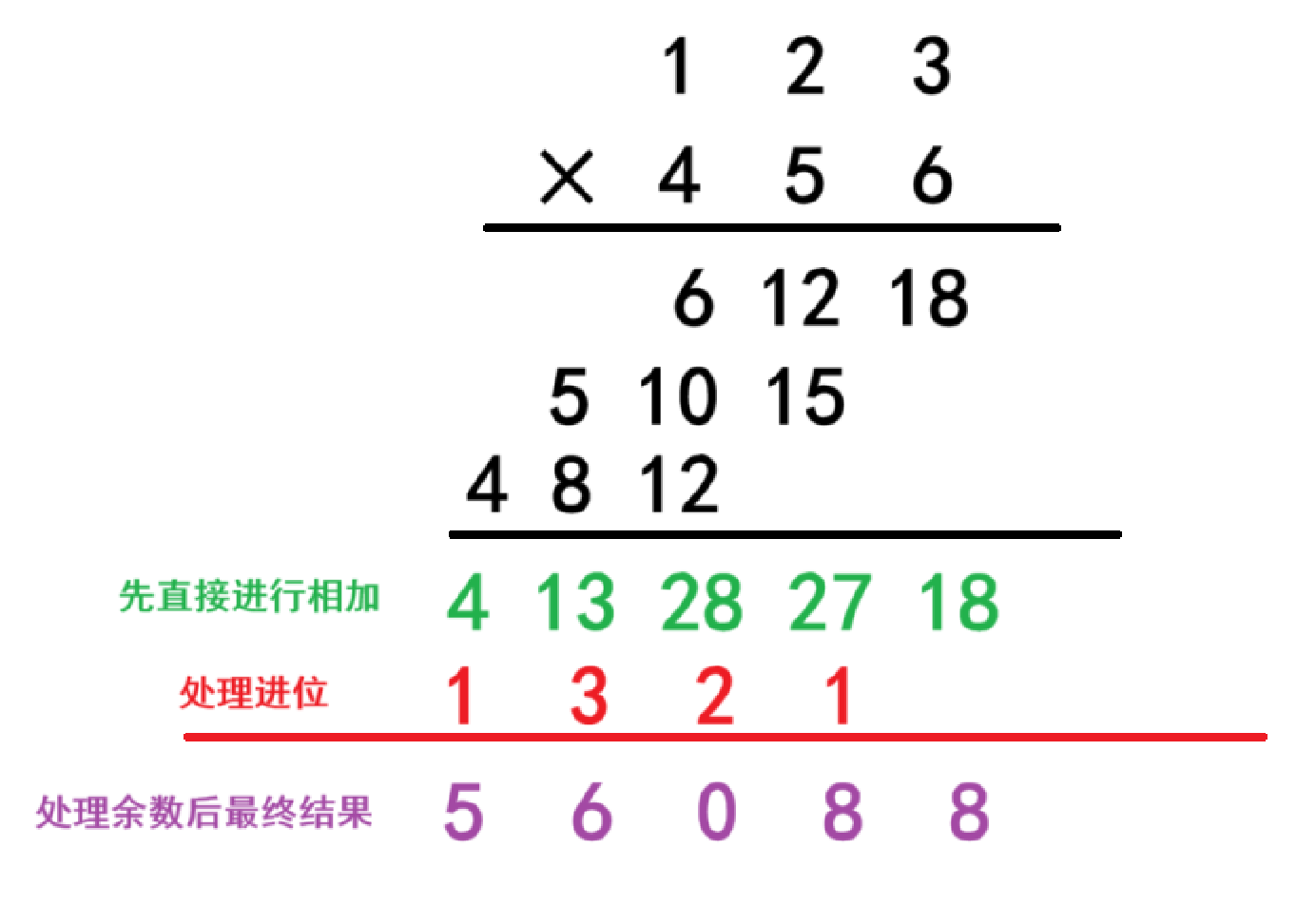
我们先直接进行逐位相乘,不用先进行进位直接保留结果,将所有位计算完后直接进行相加,就能一眼看到要进的位数了。接着处理进位和保留余数,得出来的结果和刚刚正常计算的结果是一样的,但是省去了比较繁琐的乘完一位后接着下一位就要处理进位和余数的步骤。那么如何在代码层中实现这样的过程呢。
在数组模拟里我们已经将所有数都逆序存在了数组中,每一个下标都对应的相应的位数,每一位的相乘我们可以类比对应下标的相加,最终的结果也就存放在相加后得下标的位置里。例如用3乘6等于18,对应的下标是0和0,0加0等于0,那么18就是存放在数组下标为0的位置里;接下来就是2和6相乘等于12,对应的下标是1和0,1加0等于1,那么12就是存放在数组下标为1的位置里,后面的过程也是一样的。
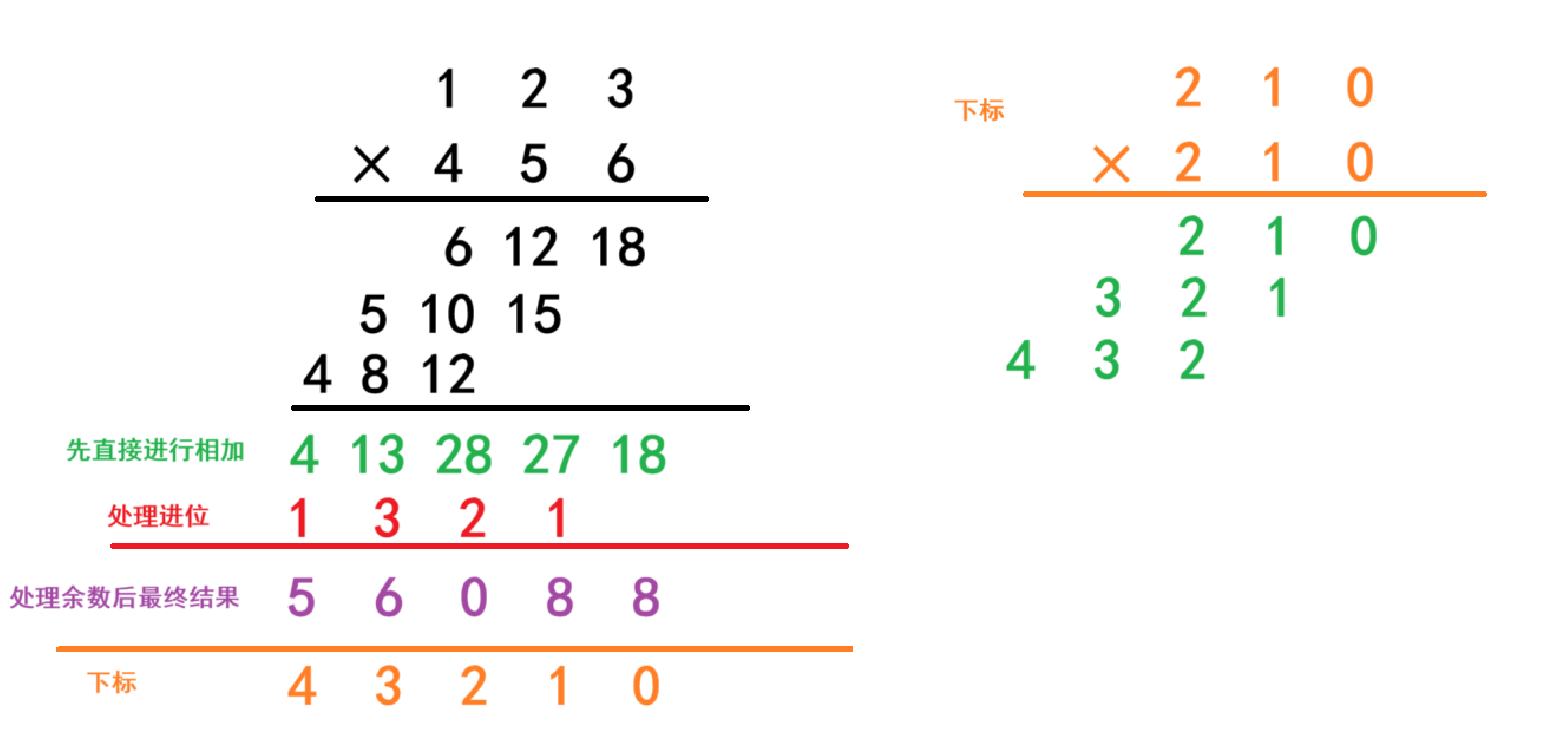
所以通过这个规律我们只需要使用两个for循环就能完成上述操作,跟咱们使用两个for循环来遍历制作出九九乘法表的项目意思是比较相似的。第一个for循环是枚举第二个数的每一位,第二个for循环则是枚举第一个数的每一位,假设第一个for循环用的是i变量,第二个for循环用的是j变量,将计算的结果就可以存放在c[i + j] += a[i] * b[j]的位置上,然后在数组c里处理进位就可以了。
接下来进行代码的实现
//高精度乘法#includeusing namespace std;const int N = 1e6 + 10;int a[N], b[N], c[N];int la, lb, lc;void mul(int c[], int a[], int b[]){//无进位相乘,然后相加for (int i = 0;i < la;i++){for (int j = 0;j < lb;j++){c[i + j] += a[i] * b[j];}}//处理进位for (int i = 0;i 1 && c[lc - 1] == 0){lc--;}}int main(){string x, y;cin >> x >> y;la = x.size();lb = y.size();lc = la + lb;//计算最高位的长度,计算的长度不会超过两者相加//拆分逆序存放for (int i = 0;i < la;i++){a[la-1-i] = x[i] - \'0\';}for (int i = 0;i = 0;i--){cout << c[i];}return 0;}运行结果

这里注意,假如要计算123乘0这种情况,在模拟计算出的结果是000,但实际只需输出一个0就行,所以要进行前导零的处理。
2.4高精度除法
讲解完了加法减法乘法,那么最终就还剩下一个高精度除法。高精度除法一般是高精度数除一个低精度数,如果是使用高精度数除一个高精度数的话,会运用上高精度减法的模拟过程,并且是无法像我们在高精度加、减、乘法这样使用小学列竖式来进行模拟的。高精度数与高精度数之间的除法在平常的也是比较少见的,主要是以高精度数除一个低精度数为多。那么在这里只给大家讲解高精度除低精度的算法讲解。
主要解法还是跟前面一样:首先读入字符串、拆分逆序存放到数组,然后利用数组来模拟小学列竖式计算除法的过程。第一步已经在前面讲解过了,咱们主要来讲解第二步。
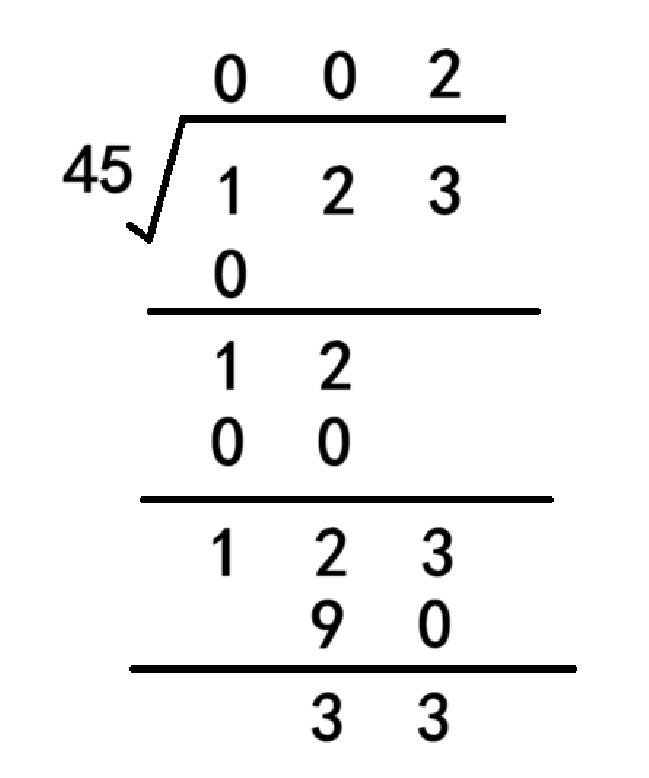
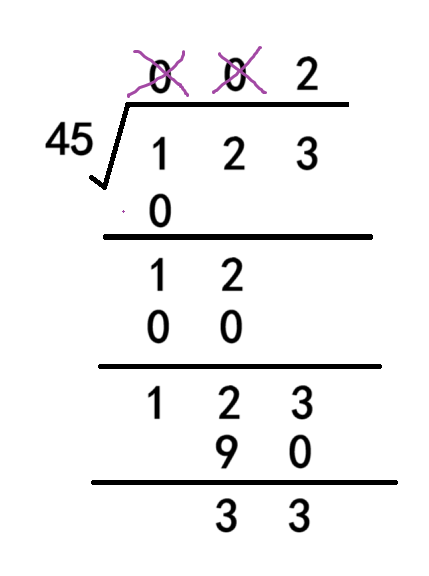
以123除45为例,先从被除数的最高位先进行计算,1除45不够商0余1,下一次计算要加上百位的2变成12再进行运算。我们可以设置一个tmp变量来存储刚刚计算的余数1,如果要加上下一位的数的话,可以先将存入余数的tmp乘10再加上下一位就行,可以用tmp = tmp * 10 + 下一位来表示。再进行计算12除45不够,继续商0余12,再将余数乘10加下一位,此时tmp为123。最后用123来除45得商为2,tmp要减去90(除数乘2)得余数为33。我们可以通过tmp / 45得到商,tmp % 45得到余数。
通过上面的模拟运算可以总结一个计算规律:
1.设一个变量tmp来一直存放余数,tmp = tmp * 10 + a[i]
2.用tmp在除上除数(b)得到商,tmp / b ——>商
3.然后用tmp模上除数(b)得到余数,tmp % b ——>余
4.最后将计算的余数再存入tmp中(如果还要再进行计算)
计算的过程主要是循环上面四个步骤,弄清楚了计算的原理,咱们可以直接进行代码展示
//高精度除法#include using namespace std;const int N = 1e6 + 10;typedef long long ll;//可能余数会超过int范围,用longlong来选择类型范围int a[N], b, c[N];int la, lc;void div(int c[], int a[], int b) //(高精度 / 低精度){ll tmp = 0;//标记每次除完之后的余数for (int i = la - 1;i >= 0;i--)//每次从最高位进行计算{//计算当前的余数tmp = tmp * 10 + a[i];//用tmp在除上除数(b)得到商c[i] = tmp / b;//处理余数tmp %= b;}//处理前导零while (lc > 1 && c[lc - 1] == 0){lc--;}}int main(){string x;cin >> x >> b;la = x.size();for (int i = 0; i = 0; i--){cout << c[i];}return 0;}运行结果
讲解一下代码中的几个点:
1.定义了longlong类型
假如要用一个10的9次方或者更大的除数来进行计算的话,那么算出来的余数肯定会超过int类型的范围(10^9),所以为了防止出现这种特殊情况,才将变量tmp的类型设置为longlong类型。
2.前导零
当从最高位开始进行除法计算时除不进,则要商0,但实际输出也是一样是不能输出前导零的,所以也要处理前导零问题。
小结
总体来看,四种算法的步骤其实大同小异,主要的还是如何将数据导入、模拟运算、解决特殊类问题等。但或许有更加优质方便简单的方法来进行计算,也希望本篇的讲解对你有所帮助。如有啥不足之处或者问题所在,欢迎大家进行评论,制作不易,也恳请大家给个三联,谢谢。