矩阵形式的FFT算法理解(Cooley-Tukey)_cooley-tukey fft算法原理程序

技术文档

长度为N的原始输入序列组成的向量为 $x\\boldsymbol x$ ，经过傅里叶变换后的序列组成的向量为 $X\\boldsymbol X$ ，则有：
$X[k]=∑n=0Ne−2πinkNx[n]\\boldsymbol X[k]=\\sum_{n=0}^{N}e^{\\frac{-2\\pi ink}{N}}\\boldsymbol x[n]$

将原始输入序列 $x\\boldsymbol x$ 划分为 $N_1$ 个长度为 $N_2=N/N_1$ 的子序列(将原序列按顺序划分为 $N1×N2N_1 \\times N_2$ 的矩阵，然后每列为一个子序列)，将第 $m$ 个子序列记为 $xm\\boldsymbol x_m$ ，原序列和子序列中的元素对应关系为：
$xm[s]=x[sN1+m]\\boldsymbol x_m[s] = x[sN_1+m]$
设序列 $xm\\boldsymbol x_m$ 的傅里叶变换为 $Xm\\boldsymbol X_m$ 。进而有：
$X[k]=∑n=0Ne−2πinkNx[n]=∑n=0Ne−2kiπ(sN1+m)Nx[sN1+m]=∑n=0Ne−2kiπmNe−2kiπsN2xm[s]=∑m=0N1e−2kiπmN∑s=0N2e−2kiπsN2xm[s]\\begin{align}\\boldsymbol X[k]&=\\sum_{n=0}^{N}e^{\\frac{-2\\pi ink}{N}}\\boldsymbol x[n] \\\\&=\\sum_{n=0}^{N}e^{\\frac{-2ki\\pi (sN_1+m)}{N}}\\boldsymbol x[sN_1+m] \\\\&=\\sum_{n=0}^{N}e^{\\frac{-2ki\\pi m}{N}}e^{\\frac{-2ki\\pi s}{N_2}}\\boldsymbol x_m[s] \\\\&=\\sum_{m=0}^{N_1}e^{\\frac{-2ki\\pi m}{N}}\\sum_{s=0}^{N_2}e^{\\frac{-2ki\\pi s}{N_2}}\\boldsymbol x_m[s]\\end{align}$
设 $WN=e2iπNW_N=e^{\\frac{2i\\pi}{N}}$ ，则有：
$X[k]=∑m=0N1WNkmXm[k%N2]\\boldsymbol X[k]=\\sum_{m=0}^{N_1}W_N^{km}\\boldsymbol X_m[k\\%N_2]$
如果将输出序列 $X\\boldsymbol X$ 划分为 $N1×N2N_1\\times N_2$ 的矩阵，矩阵中的元素和序列中的元素的对应关系为：
$Xr,c=X[rN2+c]\\boldsymbol X_{r,c}=\\boldsymbol X[rN_2 + c]$
则有：
$Xr,c=∑m=0N1WN(rN2+c)mXm[k%N2]=∑m=0N1WN1rmWNcmXm[c]\\begin{align}\\boldsymbol X_{r,c}&=\\sum_{m=0}^{N_1}W_N^{(rN_2+c)m}\\boldsymbol X_m[k\\%N_2] \\\\&=\\sum_{m=0}^{N_1}W_{N_1}^{rm}W_N^{cm}\\boldsymbol X_m[c]\\end{align}$
设：
$FN1=(WN10WN10⋯WN10WN10WN11⋯WN1N1−1⋮⋮⋮⋮WN10WN1N1−1⋯WN1(N1−1)(N1−1))F_{N_1}=\\left( \\begin{matrix} W_{N_1}^{0} & W_{N_1}^{0} & \\cdots & W_{N_1}^{0} \\\\ W_{N_1}^{0} & W_{N_1}^{1} & \\cdots & W_{N_1}^{N_1-1}\\\\ \\vdots & \\vdots & \\vdots & \\vdots \\\\ W_{N_1}^{0} & W_{N_1}^{N_1-1} & \\cdots & W_{N_1}^{(N_1-1)(N_1-1)}\\end{matrix} \\right)$

$TN1N2=(WN0WN0⋯WN0WN0WN1⋯WNN2−1⋮⋮⋮⋮WN0WNN1−1⋯WN(N1−1)(N2−1))T_{N_1N_2}=\\left( \\begin{matrix} W_{N}^{0} & W_{N}^{0} & \\cdots & W_{N}^{0} \\\\ W_{N}^{0} & W_{N}^{1} & \\cdots & W_{N}^{N_2-1}\\\\ \\vdots & \\vdots & \\vdots & \\vdots \\\\ W_{N}^{0} & W_{N}^{N_1-1} & \\cdots & W_{N}^{(N_1-1)(N_2-1)}\\end{matrix} \\right)$

$Xin=(X0[0]X0[1]⋯X0[N2−1]X1[0]X1[1]⋯X1[N2−1]⋮⋮⋮⋮XN1−1[0]XN1−1[1]⋯XN1−1[N2−1])X_{in}=\\left( \\begin{matrix} X_{0}[0] & X_{0}[1] & \\cdots & X_{0}[N_2-1] \\\\ X_{1}[0] & X_{1}[1] & \\cdots & X_{1}[N_2-1]\\\\ \\vdots & \\vdots & \\vdots & \\vdots \\\\ X_{N_1-1}[0] & X_{N_1-1}[1] & \\cdots & X_{N_1-1}[N_2-1]\\end{matrix} \\right)$
则有：
$Xout=FN1⋅(TN1N2⊙Xin)\\boldsymbol X_{out}=F_{N_1}\\cdot(T_{N_1N_2} \\odot \\boldsymbol X_{in})$
在 $Xin\\boldsymbol X_{in}$ 中每一行是一个子序列的傅里叶变换序列，这些子序列的傅里叶变换序列可以递归地使用上面的方法计算得到。一共需要递归地计算 $log_{N_1}{N}$ 轮，直到子序列中只有一个数，一个数的傅里叶变换就是其本身。每轮的计算次数为 $N_1N_1N_2+N_1N_2=(N1+1)N$ 次。故该算法的时间复杂度为 $N1+1)Nlog_{N_1}{N}$ 。

注意到：
$X[k]=∑m=0N1e−2kiπmN∑s=0N2e−2kiπsN2xm[s]\\boldsymbol X[k]=\\sum_{m=0}^{N_1}e^{\\frac{-2ki\\pi m}{N}}\\sum_{s=0}^{N_2}e^{\\frac{-2ki\\pi s}{N_2}}\\boldsymbol x_m[s]$
其中 $Xm[k]=∑s=0N2e−2kiπsN2xm[s]X_m[k]=\\sum_{s=0}^{N_2}e^{\\frac{-2ki\\pi s}{N_2}}\\boldsymbol x_m[s]$ 为 $N_2$ 点的 DFT，上面公式的含义为 $X[k]\\boldsymbol X[k]$ 的计算可以拆分为 $N_1$ 个 $N_2$ 点的 DFT 进行计算，然后再组合。而且每个 $N_2$ 点 DFT使用到的原序列中的元素为 $sN1+m,s∈{0,1,2,...,N2}sN_1+m,s\\in\\{0,1,2,...,N_2\\}$ ，对于每个序列需要固定 $m$ 。每个 $N_2$ 点 DFT使用到的原序列中的元素在原序列中并不连续，这样不方便进行迭代计算。

所以需要将原序列中的元素顺序进行调整，调整为每个 $N_2$ 点 DFT使用的元素连续存储。将原序列视为 $N1×N2N_1\\times N_2$ 的矩阵，列优先存储，然后转置即可。

其中每个 $N_2$ 点的 DFT 可以继续使用上面公式进行拆分，也需要继续对每个序列的元素顺序进行调整。

下面以 8 点 FFT 使用 radix2 为例进行说明，radix2 说明 $N_1=2$ ，首先将原序列视为 $2×42\\times 4$ 的矩阵（列优先存储）：
$[x0x2x4x6x1x3x5x7]\\left[\\begin{matrix}x_0 & x_2 & x_4 & x_6 \\\\x_1 & x_3 & x_5 & x_7 \\end{matrix}\\right]$
然后对上面矩阵转置：
$[x0x4x1x5x2x6x3x7]\\left[\\begin{matrix}x_0 & x_4 & x_1 & x_5 \\\\x_2 & x_6 & x_3 & x_7 \\end{matrix}\\right]$
将上面序列视为两个 $2×22\\times2$ 的矩阵：
$[x0x4x2x6][x1x5x3x7]\\left[\\begin{matrix}x_0 & x_4 \\\\x_2 & x_6\\end{matrix}\\right]\\left[\\begin{matrix}x_1 & x_5 \\\\x_3 & x_7\\end{matrix}\\right]$
继续对每个矩阵进行转置：
$[x0x2x4x6][x1x3x5x7]\\left[\\begin{matrix}x_0 & x_2 \\\\x_4 & x_6\\end{matrix}\\right]\\left[\\begin{matrix}x_1 & x_3 \\\\x_5 & x_7\\end{matrix}\\right]$
继续进行拆分：
$[x0x4][x2x6][x1x5][x3x7]\\left[\\begin{matrix}x_0 \\\\x_4 \\end{matrix}\\right]\\left[\\begin{matrix}x_2 \\\\x_6 \\end{matrix}\\right]\\left[\\begin{matrix}x_1 \\\\x_5 \\end{matrix}\\right]\\left[\\begin{matrix}x_3 \\\\x_7 \\end{matrix}\\right]$
再对每个子序列进行转置，由于每个子序列是 $2×12\\times 1$ 的矩阵，转置之后再拆分变为：
$[x0][x4][x2][x6][x1][x5][x3][x7]\\left[x_0 \\right]\\left[x_4 \\right]\\left[x_2 \\right]\\left[x_6 \\right]\\left[x_1 \\right]\\left[x_5 \\right]\\left[x_3 \\right]\\left[x_7 \\right]$
到此步每个子序列的长度为 1，其傅里叶变换为其本身，将其表示如下（下面所有矩阵都是行优先）：
$[Z0[0]][Z1[0]][Z2[0]][Z3[0]][Z4[0]][Z5[0]][Z6[0]][Z7[0]]\\left[Z_0[0] \\right]\\left[Z_1[0] \\right]\\left[Z_2[0] \\right]\\left[Z_3[0] \\right]\\left[Z_4[0] \\right]\\left[Z_5[0] \\right]\\left[Z_6[0] \\right]\\left[Z_7[0] \\right]$
下面开始按照 $Xout=FN1⋅(TN1N2⊙Xin)\\boldsymbol X_{out}=F_{N_1}\\cdot(T_{N_1N_2} \\odot \\boldsymbol X_{in})$ 进行合并计算：
$[G0[0]G0[1]]=[W20W20W20W21]⋅([W20W20]⊙[Z0[0]Z1[0]])\\left[\\begin{matrix}G_0[0] \\\\G_0[1] \\end{matrix}\\right]=\\left[\\begin{matrix}W_2^0 & W_2^0 \\\\ W_2^0 & W_2^1 \\end{matrix}\\right]\\cdot \\left(\\left[\\begin{matrix}W_2^0 \\\\W_2^0 \\end{matrix}\\right]\\odot\\left[\\begin{matrix}Z_0[0] \\\\Z_1[0] \\end{matrix}\\right]\\right)$
对八个个子序列分别进行合并计算得到4个 2 点 DFT 序列：
$[G0[0]G0[1]][G0[0]G1[1]][G0[0]G2[1]][G0[0]G3[1]]\\left[\\begin{matrix}G_0[0] \\\\G_0[1]\\end{matrix}\\right]\\left[\\begin{matrix}G_0[0] \\\\G_1[1]\\end{matrix}\\right]\\left[\\begin{matrix}G_0[0] \\\\G_2[1]\\end{matrix}\\right]\\left[\\begin{matrix}G_0[0] \\\\G_3[1]\\end{matrix}\\right]$
继续进行下一轮合并：
$[F0[0]F0[1]F0[2]F0[3]]=[W20W20W20W21]⋅([W40W40W40W41]⊙[G0[0]G0[1]G1[0]G1[1]])\\left[\\begin{matrix}F_0[0] & F_0[1]\\\\F_0[2] & F_0[3]\\end{matrix}\\right]=\\left[\\begin{matrix}W_2^0 & W_2^0 \\\\ W_2^0 & W_2^1 \\end{matrix}\\right]\\cdot \\left(\\left[\\begin{matrix}W_4^0 & W_4^0\\\\W_4^0 & W_4^1\\end{matrix}\\right]\\odot\\left[\\begin{matrix}G_0[0] & G_0[1]\\\\G_1[0] & G_1[1]\\end{matrix}\\right]\\right)$
对四个子序列分别进行合并计算得到 2 个 4 点的 DFT 序列：
$[F0[0]F0[1]F0[2]F0[3]][F1[0]F1[1]F1[2]F1[3]]\\left[\\begin{matrix}F_0[0] & F_0[1]\\\\F_0[2] & F_0[3]\\end{matrix}\\right]\\left[\\begin{matrix}F_1[0] & F_1[1]\\\\F_1[2] & F_1[3]\\end{matrix}\\right]$
最后一步，对两个子序列进行合并计算得到最终的 8 点 DFT 序列：
$[X[0]X[1]X[2]X[3]X[4]X[5]X[6]X[7]]=[W20W20W20W21]⋅([W80W80W80W80W80W81W82W83]⊙[F0[0]F0[1]F0[2]F0[3]F1[0]F1[1]F1[2]F1[3]])\\left[\\begin{matrix}X[0] & X[1] & X[2] & X[3] \\\\ X[4] & X[5] & X[6] & X[7]\\end{matrix}\\right]=\\left[\\begin{matrix}W_2^0 & W_2^0 \\\\ W_2^0 & W_2^1 \\end{matrix}\\right]\\cdot \\left(\\left[\\begin{matrix}W_8^0 & W_8^0 & W_8^0 & W_8^0 \\\\W_8^0 & W_8^1 & W_8^2 & W_8^3\\end{matrix}\\right]\\odot\\left[\\begin{matrix}F_0[0] & F_0[1] & F_0[2] & F_0[3]\\\\F_1[0] & F_1[1] & F_1[2] & F_1[3] \\end{matrix}\\right]\\right)$
计算过程表示为如下图：

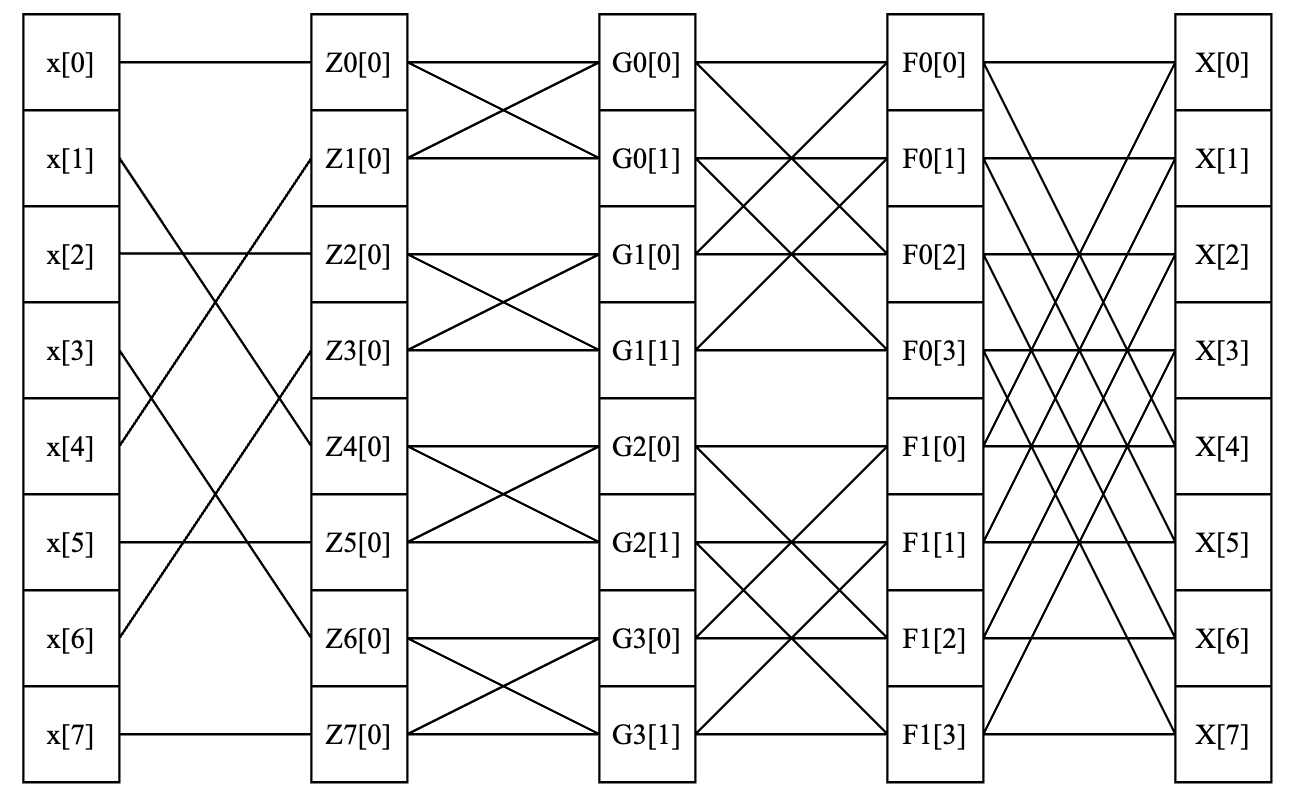
矩阵形式的FFT算法理解(Cooley-Tukey)_cooley-tukey fft算法原理程序

所以矩阵形式的 FFT 算法设计思路为：

对序列长度进行分解，确定 radix序列

例如上面例子中将长度 8 分解为 $2×2×22\\times 2\\times 2$ ，即三次 radix2 的合并计算

如果是 512 的序列可以分解为 $2×16×162\\times 16\\times 16$ ，即一次 radix2 和两次 radix16 合并
通过矩阵转置对原序列进行重新排列，也即位置换

如果是上面 512 的序列分解为 $2×16×162\\times 16\\times 16$ ，首先将 512 序列视为列优先 $2×2562\\times256$ 的矩阵进行转置，再将其分为两个 256 的序列，每个序列视为 $16×1616\\times16$ 的列优先矩阵进行转置，最后将其分解为 16 个长度为 16 的序列，对每一个序列，将其视为 $16×116\\times1$ 的矩阵进行转置。最后将所有序列顺序排布即可。
迭代对子序列进行合并，将短的 DFT 序列合并为长的 DFT 序列

算法实现如下：

import numpy as npdef generate_matrix(n1, n2, dft): if dft : len = n1 else: len = n1 * n2 # print(len) matrix = np.ones((n1, n2)) + 1.j * np.zeros((n1, n2)) w = np.cos(2 * np.pi / len) - 1.j * np.sin(2 * np.pi / len) for i in range(1, n2): matrix[1, i] = matrix[1, i - 1] * w for i in range(2, n1): matrix[i, :] = matrix[i - 1, :] * matrix[1, :] # for i in range(n1): # for j in range(n2): # matrix[i][j] = np.exp(-2j * np.pi * i * j / len) return matrixdef bit_reverse(x, len, batch, radix_list): tlen = len * batch n2 = len for radix in reversed(radix_list): n1 = radix n2 = n2 // radix x = np.transpose(x.reshape(batch, n2, n1), (0, 2, 1)).flatten() batch = batch * radix return xdef find_raidx_list(len): radix = [16, 8, 4, 2] list = [] for r in radix: while len % r == 0: list.append(r) len = len // r return listdef stockham_fft(x, len, batch, radix_list): tlen = len * batch n2 = 1 X = x for radix in radix_list: n1 = radix batch = tlen // n1 // n2 X = X.reshape((batch, n1, n2)) print(X.shape) tw_matrix = generate_matrix(n1, n2, 0) X *= tw_matrix dft_matrix = generate_matrix(radix, radix, 1) X = dft_matrix @ X n2 = n2 * radix return X.flatten()N = 8192x = np.random.uniform(0, 1, (N,)) + 1.j * np.random.uniform(1, 1, (N,))# x =np.array([1+1j, 2+1j, 3+1j, 4+1j])# print(x)np_fft_X = np.fft.fft(x)radix_list = find_raidx_list(N)# radix_list = [2, 2, 2]x = bit_reverse(x, N, 1, radix_list)X = stockham_fft(x, N, 1, radix_list)# print(X)# print(np_fft_X)print(\"isCorrect: \", np.allclose(X, np_fft_X))

矩阵形式的FFT算法理解(Cooley-Tukey)_cooley-tukey fft算法原理程序

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

矩阵形式的FFT算法理解(Cooley-Tukey)_cooley-tukey fft算法原理程序

相关问题

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载