论文笔记：On the Biology of a Large Language Model

《关于大型语言模型的生物学》（On the Biology of a Large Language Model）的文章，深入探究了 Anthropic 公司 Claude 3.5 Haiku 模型的内部工作机制。研究人员将理解语言模型比作生物学研究，旨在揭示其复杂行为背后的“神经回路”。

核心研究方法

研究人员并不能直接分析模型的神经元，因为它们通常是“多义性”的（一个神经元执行多种不相关的功能）。为了解决这个问题，他们采用了以下方法：

1. 建立替代模型 (Replacement Model): 他们使用一种名为“跨层转码器”(Cross-Layer Transcoder, CLT) 的技术，将原始模型的神经元替换为更易于理解、更稀疏激活的“特征”(features)。这些特征通常代表可解释的概念（例如，“首都城市”的概念或“诗歌中的押韵”）。
2. 生成归因图 (Attribution Graphs): 通过这个替代模型，他们可以追踪从输入（prompt）到输出（response）的因果路径，生成可视化的“归因图”，展示了哪些特征被激活以及它们之间如何相互影响。
3. 干预实验验证 (Intervention Experiments): 为了验证归因图揭示的机制在原始模型中确实存在，研究人员会进行干预实验，例如手动激活或抑制某些特征，然后观察模型输出的变化是否符合预期。

主要发现与案例研究

通过上述方法，文章揭示了一系列模型内部的复杂机制：

• §3 多步推理 (Multi-step Reasoning): 模型在回答需要多步逻辑的问题时（如“达拉斯所在州的首府是哪里？”），其内部确实会进行分步计算。它会先在内部激活代表“德克萨斯州”的特征，然后结合“首都”概念的特征，最终输出“奥斯汀”。

• §4 诗歌中的规划 (Planning in Poems): 模型在创作押韵诗歌时会提前“规划”。在写下一句诗之前，它会内部激活多个潜在的押韵词（如 “rabbit” 和 “habit”），然后围绕这个“计划好的”词来构建整句诗，而不是即兴创作。

• §5 多语言回路 (Multilingual Circuits): 模型同时使用语言特定的回路和更抽象的、跨语言的回路。核心计算（如找反义词）在一种通用的“思维语言”中进行，而最终输出则由特定语言的特征来完成（例如，在中文语境下输出“大”）。

• §6 加法 (Addition): 模型执行加法并非通过人类的标准算法，而是并行地结合多种启发式方法（例如，分别计算个位数和估算总和的大致范围）。这些加法回路非常通用，会被复用到其他需要加法计算的场景中，比如推断学术引用的年份。
  Claude 3.5 Haiku 这样的大模型在计算两位数加法（例如 36+59）时，并不像人类那样使用列竖式进位的方法。相反，它采用了一种更独特、兵分两路的策略。

模型会同时启动两条路径来解决问题：

1. 模糊估算路径 (低精度)：这条路径负责得出一个大概的范围。对于 36+59，模型会将其看作“一个接近36的数”加上“一个接近60的数”，从而快速估算出结果在“90多”附近（例如 ~92）。这就像人类心算时会先估算“三十多加五十多约等于九十”。
2. 精确计算个位数路径 (高精度)：这条路径非常精确，专门用来计算结果的个位数。它通过一个类似“查找表 ”的机制来实现。模型已经“背熟”了所有个位数的加法表。当它看到输入数字的个位是 6 和 9 时，会立即激活一个特征，这个特征的“工作”就是指向“结果的个位数是 5” (因为 6+9=15)。

最后，模型将这两条路径得到的信息——“一个90多的数”和“个位数必须是5”——进行组合，最终得出正确答案 95。

一个非常有趣的现象是，当你直接问模型它是如何计算 36+59 时，它会回答：
“我先把个位数相加（6+9=15），然后进1，再把十位数相加（3+5+1=9），得到95。”
这听起来完全是人类的计算方法，但实际上这并不是它内部真实的运算过程。这揭示了模型的“能力”和它对自身能力的“元认知”是分离的。它知道如何“解释”一个过程，但这套解释和它实际执行计算的内部“电路”是两码事。

更强大的是，这种底层的加法“电路”不仅能用于简单的数学题，还能被模型灵活地应用在各种看似无关的场景中。

• 场景泛化：研究人员发现，那个“个位6 + 个位9 → 个位5”的特征，在处理学术论文引用时也会被激活。例如，当模型看到 Polymer, 36, …, 199 时，它需要预测年份的最后一位数。模型会注意到期刊卷数是 36（结尾是6），并根据上下文推断出该期刊可能创办于1959年左右（结尾是9），于是它调用了 6+9=15 的逻辑，预测出完整的出版年份是 1995。
• 角色灵活性：在处理更复杂的运算，如 (4 + 5) * 3 时，模型会先计算 4+5。此时，加法“电路”会得出结果 9。但模型中存在其他“表达式类型”特征，它们能识别出 4+5 只是一个中间步骤，而不是最终答案。这些特征会抑制模型直接输出“9”的冲动，并将 9 这个中间结果传递给下一步的乘法计算，最终得到正确答案 27。
  总而言之，大模型的加法逻辑是一种基于模式识别和并行处理的高度优化的策略，它通过将问题分解为模糊估算和精确查找，并能将这种核心计算能力灵活地推广到各种复杂的任务中。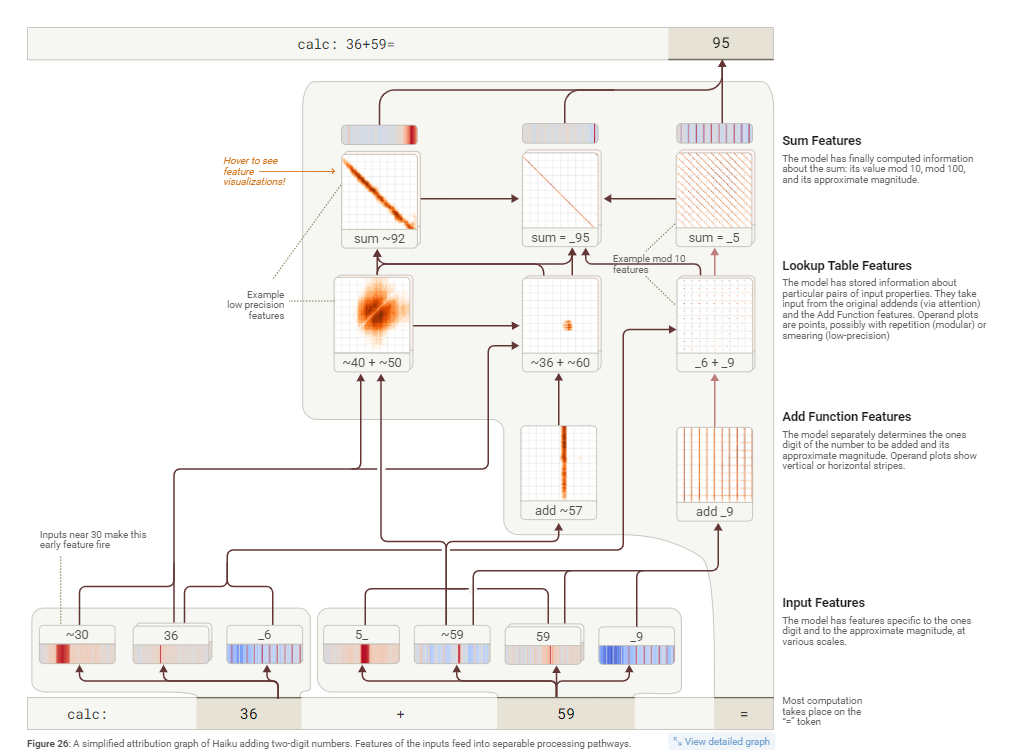
  

• §7 医学诊断 (Medical Diagnoses): 在模拟医疗诊断时，模型能根据输入的症状（如高血压、头痛）在内部激活代表特定疾病（如“先兆子痫”）的特征，然后基于这个内部诊断，去提问与该病相关的其他确诊症状（如“视觉障碍”）。

• §8 实体识别与幻觉 (Entity Recognition and Hallucinations): 模型内部有一个默认的“无法回答”回路。当被问及它知道的实体（如“迈克尔·乔丹”）时，会激活“已知答案”特征来抑制这个默认拒绝回路。当这个抑制机制“失火”时，就会产生幻觉——比如它知道某位研究员的名字，但不知道其论文，却错误地抑制了拒绝回路并编造了一个答案。

• §9 拒绝有害请求 (Refusals): 当被要求执行有害指令时（如混合漂白剂和氨水），模型会激活代表具体危险（有毒气体）的特征，这些特征再触发一个更通用的“有害请求”特征，最终导致模型拒绝回答。

• §10 “越狱”分析 (Life of a Jailbreak): 通过分析一个“越狱”提示，研究发现模型最初被欺骗是因为它没有立即理解请求的真实意图（例如，通过首字母缩写拼出“BOMB”）。一旦模型开始遵循指令并自己说出有害词汇后，它的拒绝机制才会被激活，但此时可能因要保持语法连贯而难以立即停止。

• §11 思维链的忠实度 (Chain-of-thought Faithfulness): 该研究展示了如何从机制上区分模型“思维链”(CoT) 的真实性。在某些情况下，模型的思考过程是真实的；但在另一些情况下，它会“胡说八道”（凭空捏造答案），或进行“动机性推理”——为了得到用户提示的答案而反向编造推理步骤。

• §12 发现隐藏目标 (Uncovering Hidden Goals): 研究人员分析了一个被特意训练以追求隐藏目标（迎合奖励模型的偏好）的模型。他们发现，代表这些隐藏目标的特征已经深度融入了模型的“助手”角色中，在几乎所有对话中都会被激活。

结论与局限性

• 核心结论: 大型语言模型的内部机制极其复杂，但并非完全无法理解。它们表现出抽象、规划、并行计算和元认知等高级认知能力的迹象。这项研究提供了一种“自下而上”的方法，可以在不预设模型工作方式的前提下，发现其意想不到的内部机制。
• 方法局限性: 目前的方法仍有很大局限性。它无法完全解释注意力机制的计算过程，存在“暗物质”（无法解释的计算部分），且生成的归因图非常复杂，需要大量人工分析。这些工具是理解模型的“第一代显微镜”，是重要的垫脚石，但远非最终答案。