【递归,搜索与回溯算法篇】专题(一) - 递归

文章目录
面试题 08.06. 汉诺塔问题
题目链接: 面试题 08.06. 汉诺塔问题
题目描述:
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
示例 1:
输入:A = [2, 1, 0], B = [], C = []
输出:C = [2, 1, 0]
示例 2:
输入:A = [1, 0], B = [], C = []
输出:C = [1, 0]
提示:
A 中盘子的数目不大于 14 个。
题目解析:
- 小规模问题分析
当N = 1时:直接移动
//将盘子直接从a移动到ca -> c
当N = 2时:先将最小的盘子从a移到b,再将大盘从a移到c,再将小盘从b移到c。
//先把小盘子从a移动到ba -> b//再把大盘子从a移动到ca -> c//最后把小盘子从b移动到cb -> c
当N = 3时:先将前两个盘子借助c从a移动到b,再将最大的盘子移动到c,将前两个盘子借助a从b移动到c。
//将前两个盘子从a移动到b(借助c)a -> ca -> bc -> b//将最大的盘子从a移动到ca -> c//将b上面的两个盘子从b移动到c(借助a)b -> ab -> ca -> c
- 这道题为什么可以使用递归?
解决大问题时出现了相同的子问题,在解决子问题时又出现了相同的子问题。 - 如何编写递归代码?
1.重复子问题 -> 函数头
函数头:将x柱子上的一堆盘子,借助y柱子,转移到z柱子上。n代表盘子的数量
void dfs(x , y , z , int n )
2.只关心某一个子问题在做什么 -> 函数体
函数体:
将x柱子上的n-1个盘子借助z柱子放到y柱子上
dfs(x , z , y , n-1)
将x柱子最大的盘子放到z柱子上
x.back() -> z
将y柱子上的n-1个盘子借助x盘子放到z柱子上
dfs(y , x , z , n-1)
当剩最后一个盘子时,直接从a柱子移动到c柱子
x.back -> z
代码实现:
class Solution {public: void hanota(vector<int>& A, vector<int>& B, vector<int>& C) { dfs(A,B,C,A.size()); } void dfs(vector<int>& A, vector<int>& B, vector<int>& C,int n) { if(n == 1) { C.push_back(A.back()); A.pop_back(); return; } dfs(A,C,B,n-1); C.push_back(A.back()); A.pop_back(); dfs(B,A,C,n-1); }};21. 合并两个有序链表
题目链接: 21. 合并两个有序链表
题目描述:
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
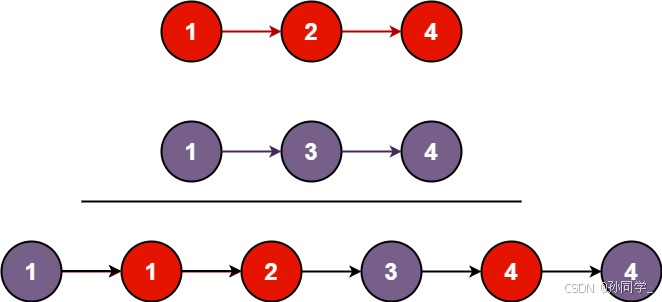
示例 1:
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
示例 2:
输入:l1 = [], l2 = []
输出:[]
示例 3:
输入:l1 = [], l2 = [0]
输出:[0]
提示:
- 两个链表的节点数目范围是 [0, 50]
- -100 <= Node.val <= 100
- l1 和 l2 均按 非递减顺序 排列
题目解析:
这道题让我们将两个升序链表合并为一个新的升序链表,我们用递归的解法就是先找出l1和l2头节点小的那一个,让它作为新的链表的头节点。然后在剩下的两个链表中继续去找小的那个作为链表的头节点。此时就出现了相同的子问题。
- 相同的子问题 -> 函数头的设计
Node* dfs(Node* l1,Node* l2) - 某个子问题在干什么 -> 函数体的设计
先判断两个头指针的大小,谁小谁当最后的头指针
①比大小
②让小的那个连接剩下的两个链表合并后的结果
小->next = dfs(小->next,大)
return 小; - 递归的出口
谁为空返回另一个
代码实现:
class Solution {public: ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) { if(l1 == nullptr) return l2; if(l2 == nullptr) return l1; if(l1 -> val <= l2 -> val) { l1 -> next = mergeTwoLists(l1 -> next,l2); return l1; } else { l2 -> next = mergeTwoLists(l1,l2 -> next); return l2; } }};206. 反转链表
题目链接: 206. 反转链表
题目描述:
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:

输入: head = [1,2,3,4,5]
输出: [5,4,3,2,1]
示例 2:

输入: head = [1,2]
输出: [2,1]
示例 3:
输入: head = []
输出:[]
题目解析:
这道题给了我们一个单链表的头节点,让我们反转链表,然后返回反转后的链表。
第一种视角:从宏观的角度来看待这个问题
将head的next的next指向head,将head的next置为空。
如此我们会发现这将会导致结点丢失

比如上述操作会使得3这个结点丢失。
我们用递归的方法来解决这道问题
1.我们先让当前结点后面的链表先逆置,并且把头节点返回。
2.把当前结点添加到逆置后的结点的后面即可。
第二种视角:将链表看成一棵树
链表其实是一种特殊的树形结构,仅需对链表做一次深度优先遍历即可。

我们定义一个newhead对链表做一次深度优先遍历,当newhead的next为空时说明此结点就是将来要返回的头节点
- 重复子问题 -> 函数头的设计
传入一个头节点,从后向前反转链表 - 子问题在干什么 -> 函数体的设计
将此结点的next的next指向此节点,此节点的next置为空 - 返回值
返回next为空的结点
代码实现:
class Solution {public: ListNode* newhead; //定义一个newhead记录要返回的新的头节点 ListNode* reverseList(ListNode* head) { if(head == nullptr || head -> next == nullptr) return head; auto newhead = reverseList(head -> next); head -> next -> next = head; head -> next = nullptr; return newhead; }};24. 两两交换链表中的节点
题目链接: 24. 两两交换链表中的节点
题目描述:
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:

输入: head = [1,2,3,4]
输出: [2,1,4,3]
示例 2:
输入: head = []
输出: []
示例 3:
输入: head = [1]
输出: [1]
题目解析:
这道题目让我们两两交换相邻的节点,并返回交换后链表的头节点,前提是在不修改节点中的值的情况下,即只能进行节点交换。这道题我们可以用递归的思路来求解。首先定义一个ret来用来接收交换后链表的头节点。然后把相邻节点进行两两交换。
代码实现:
class Solution {public: ListNode* swapPairs(ListNode* head) { if(head == nullptr || head->next == nullptr) return head;//如果链表为空或者链表的下一个节点为空,直接返回头节点 ListNode* r = swapPairs(head->next->next); ListNode* ret = head->next; head->next->next = head; head->next = r; return ret; }};50. Pow(x, n)
题目链接: 50. Pow(x, n)
题目描述:
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,x的n次方)。
示例 1:
输入: x = 2.00000, n = 10
输出: 1024.00000
示例 2:
输入: x = 2.10000, n = 3
输出: 9.26100
示例 3:
输入: x = 2.00000, n = -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25
题目解析:
这道题让我们计算x的n次方。
解法一: 暴力解法
我们可以用一个循环进行暴力求解,但是对这道题而言暴力求解会超出时间限制。
解法二: 快速幂
实现快速幂的方法有两种,第一种是递归,第二种是循环。本题我们就来用递归的方式实现快速幂。
例如:我们要求3的16次方,我们可以先求出3的8次方,要求3的8次方,我们可以先求出3的4次方,要求3的4次方,我们可以先求出3的平方。

当n为奇数时,我们可以先求出x的二分之n次方,最后再乘上x。

- 相同的的子问题 -> 函数头的设计
给一个数和一个指数,求出x的n次幂是多少
int Pow( x , n ) - 只关心某一层在干什么 -> 函数体的设计
给一个数和一个指数,求出x的n/2次幂是多少
tmp = Pow( x , n / 2 ) - 返回值
分类讨论
如果n为偶数,返回tmp*tmp
如果n为奇数,返回tmp*tmp*x
代码实现:
class Solution{public: double myPow(double x, int n) { return n < 0 ? 1.0 / pow(x, -(long long)n) : pow(x,n); } double pow(double x, long long n) { if(n == 0) return 1.0; double tmp = pow(x ,n / 2); return n % 2 == 0 ? tmp * tmp : tmp * tmp * x; }};👍 如果对你有帮助,欢迎:
- 点赞 ⭐️
- 收藏 📌
- 关注 🔔


