【动态规划】01背包问题应用_我们将这些重量分成两组:编号不大于 t的重量和编号大于 t的重量,对于某

01背包问题应用

• 1.分割等和子集
• 2.目标和
• 3.最后一块石头的重量 II

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励，我们一起努力吧!😃😃

1.分割等和子集

题目链接：416. 分割等和子集

题目分析：

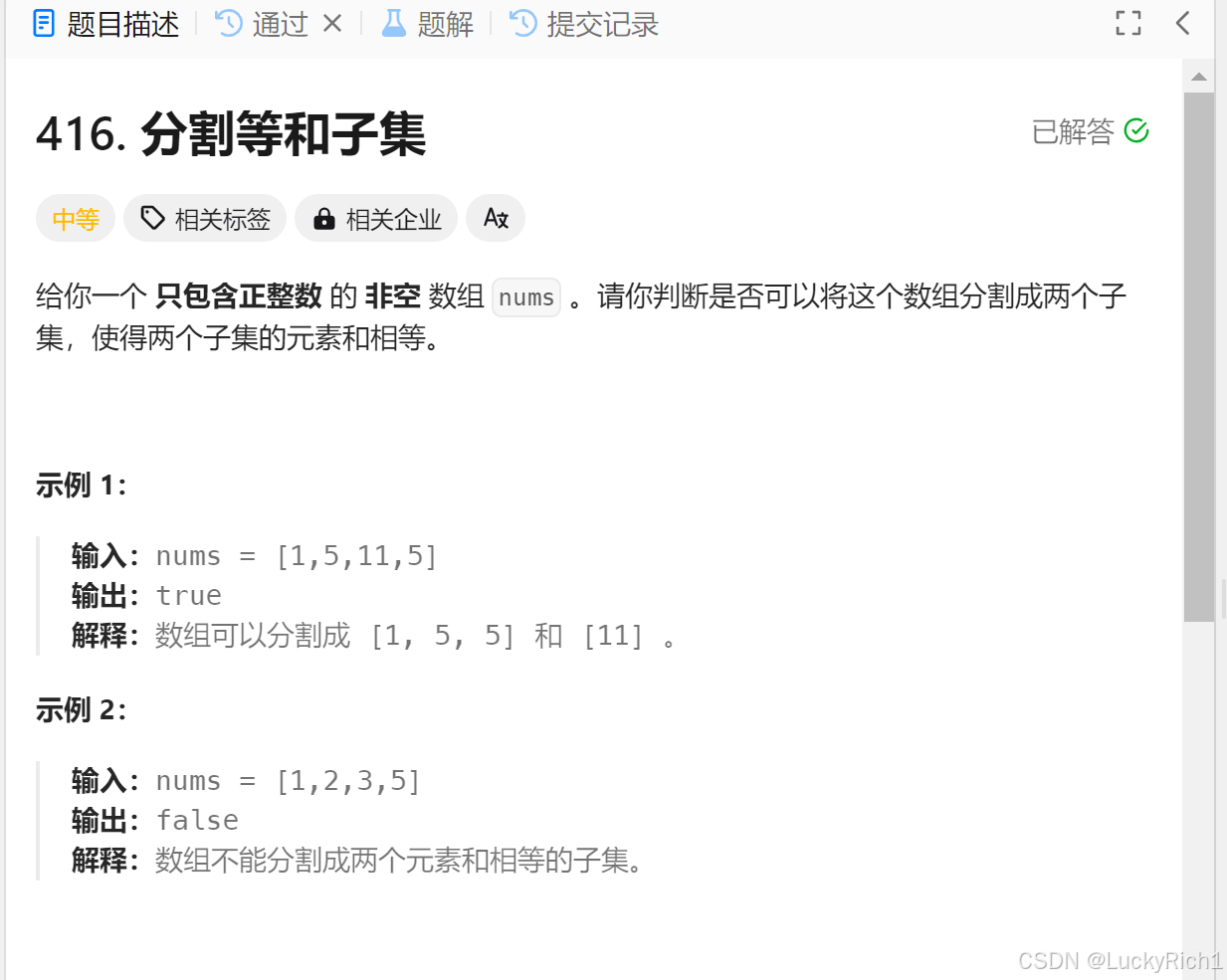
给一个 只包含正整数 的 非空 数组 nums 。判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

算法原理：

在用动态规划之前我们先分析一下，如果这道题直接把数组拆分成两部分，你会发现非常难做。所以我们要把问题的题干转换一下。

这道题重点是：将这个数组分割成两个子集，使得两个子集的元素和相等。

假设原始数组的和为sum，将它分成两个子集并且和相等，那每个子集和都是sum/2。

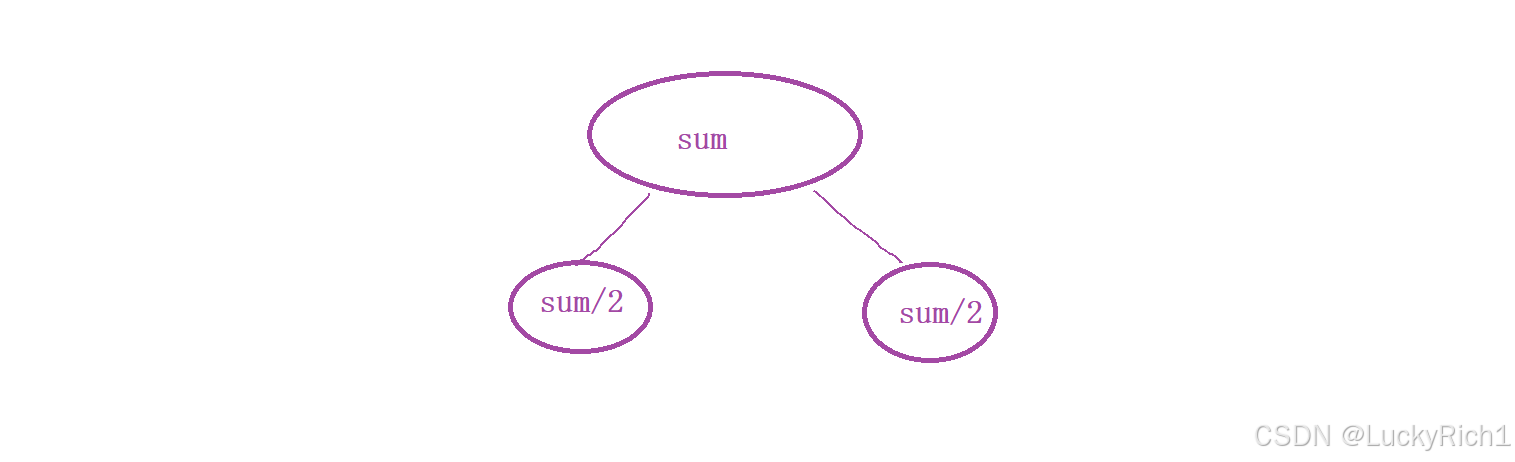
其次我们仅需解决左边一个子集就可以了，右边我们就不考虑了。因为整个数组的和是不变的。只要能挑选出一些元素让左边子集的和为sum/2，右边自然也是sum/2。

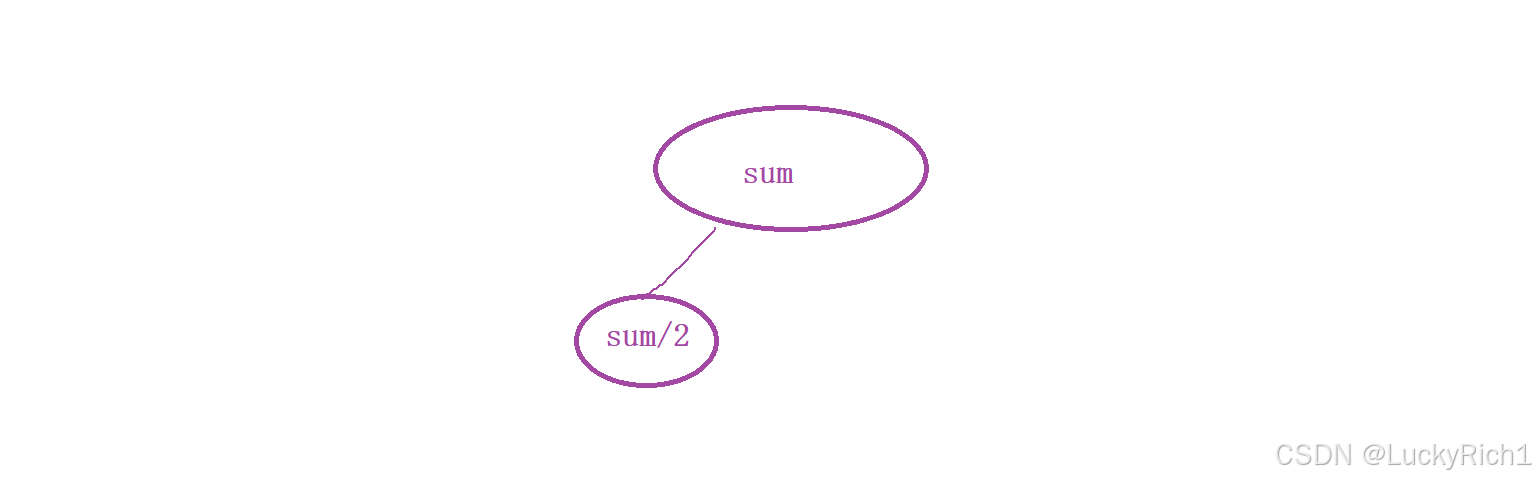
所以这道题就可以转化成：

在数组中选择一些数出来，让这些数的和等于 sum/2

那如何解决这个问题呢？

我们可以从左往右开始选，数组中每一个数都有选or不选两种情况。然后我们从这些数挑一些出来正好等于sum/2。

这是不是和01背包的问题一模一样。

回顾一下01背包问题，给一些物品，每个物品都只有1个，都面临选or不选两种情况。然后挑一些物品放背包里面，在背包容量可以承受情况下求最大价值。

这道题我们可以把每一个数当成一个物品，相当于我们有一个背包容量是sum/2。每个物品都有一个面临选or不选两种情况，把这些物品挑选出来装到背包里，把背包装满即可。

这道题比01背包简单，01背包每个物品不仅右体积还有价值，而我们这里只有体积。我们仅需把背包装满就可以了。然后每个物品只有1个面临选or不选两种情况，像这种问题我们转换为01背包问题。

之前01背包哪里说过，01背包是一个模板。模板的意思是并不是把哪里的状态表示，状态转移方程直接照抄。而照抄的应该是里面的分析思路。 如何定义状态表示可以照抄一下01背包，如何推导状态转移方程照抄一下01背包。要根据题目要求做些微调的，比如01背包要求最大价值。这里我们这里仅需考虑能否装满这个背包就可以了。

1.状态表示

这里我们不用考虑最大价值，所以我们的状态表示可以这样定义：

dp[i][j] 表示：从前 i 个数中选，所有选法中，能否凑成 j 这个数

2.状态转移方程

根据最后一个位置，划分问题：

不选 i ，那仅在 0 ~ i - 1 选看能否凑成 j

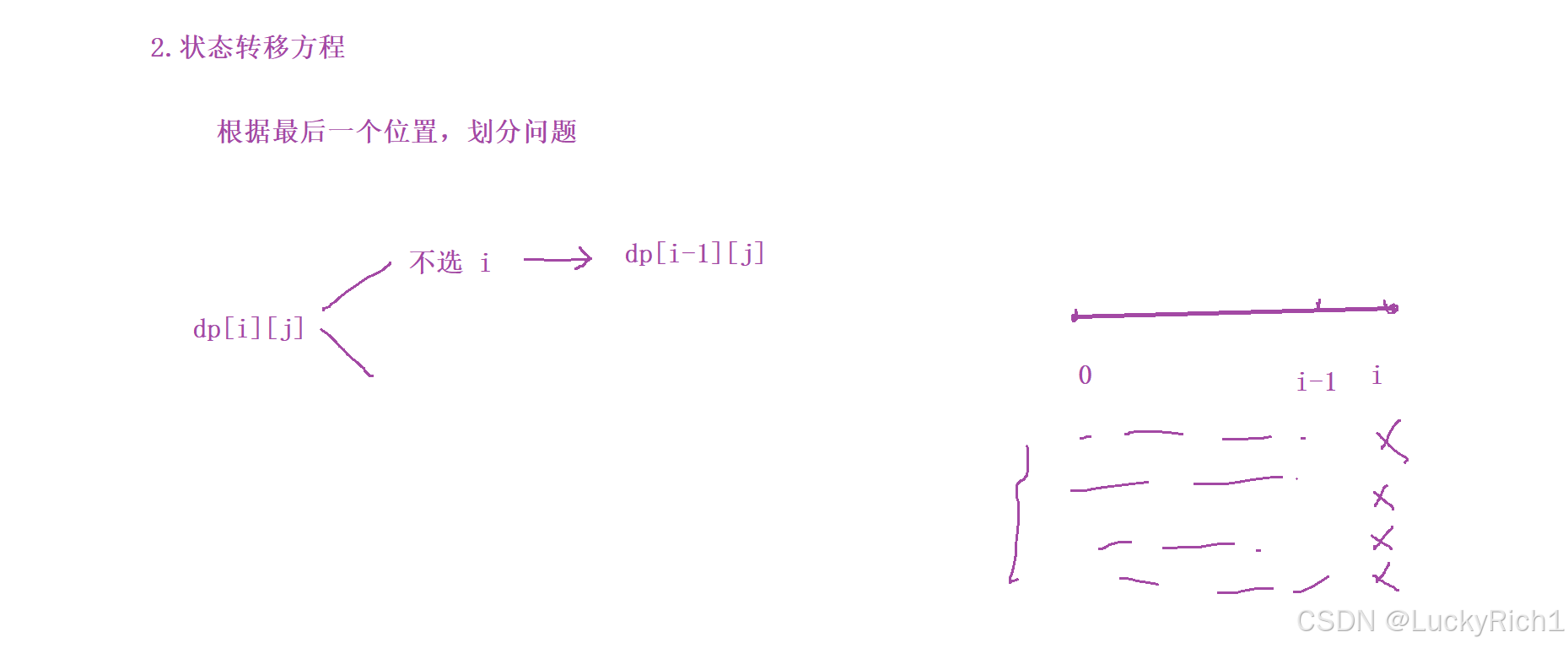
选 i，所有选法都包含 i ，接下来看能否凑成 j。i 必选 相当于已经有一个nums[i]了，接下来在 0 ~ i - 1选凑成 j - nums[i] 就可以了。但是 j - nums[i] 不一定存在。
如果nums[i]比j还大， j - nums[i] 就变成负数。因此必须 j >= nums[i]

我们要的是能否，因此只要两种情况有一个成立即可

3.初始化

1. 多开一行一列
2. 里面的值要保证后序的填表是正确的
3. 下标的映射关系

第一行表示数组为空，第一列表示 j 为空。

如果第一行为空，凑成和为0，当然是可以的。

那想凑成后面1、2、3…，根本不可能

如果第一列为空，表示 j 为空，数组虽然不为空，但是我不选就可以凑成 j = 0

4.填表顺序

从上往下填写每一行

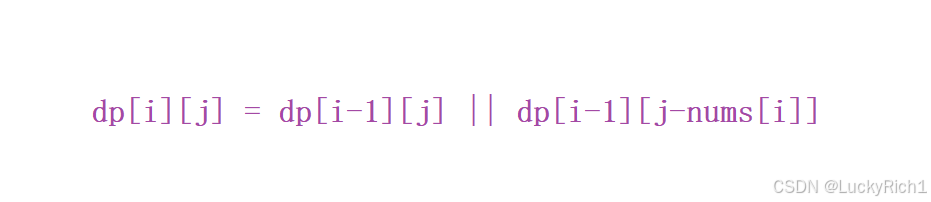
5.返回值

dp[i][j] 表示：从前 i 个数中选，所有选法中，能否凑成 j 这个数。我们要的是整个数组能否凑成sum/2这个数。因此返回dp[n][sum/2]

class Solution { public: bool canPartition(vector<int>& nums) {  // 预处理 int sum = 0; for(auto e: nums) sum += e;  if(sum % 2) return false; // 1.创建 dp 表 // 2.初始化 // 3.填表 // 4.返回值 int n = nums.size(); int aim = sum / 2; vector<vector<bool>> dp(n + 1,vector<bool>(aim + 1)); for(