优选算法：移动零

题目链接

移动零

 

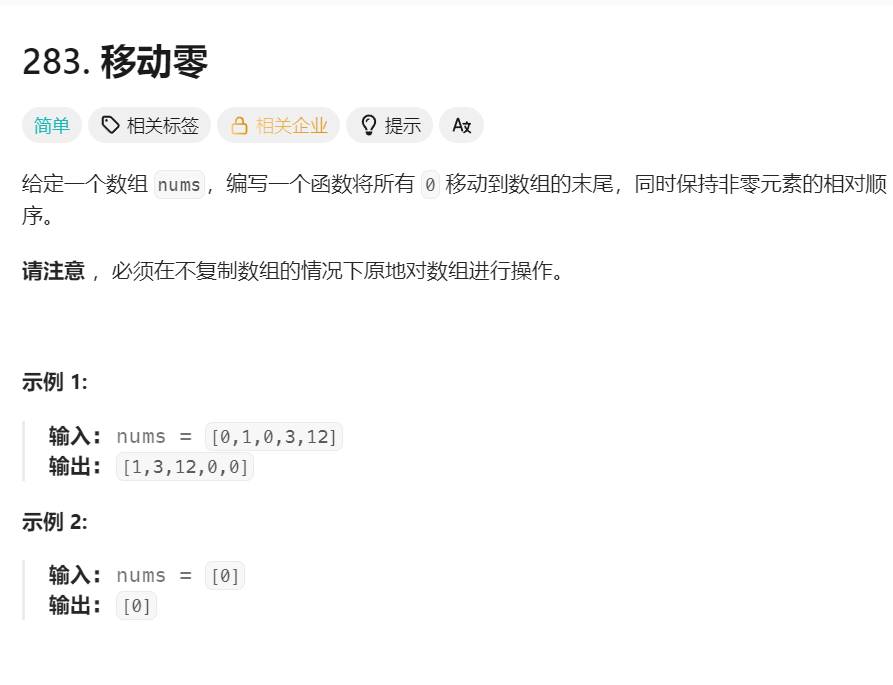
题目描述

 

核心思路

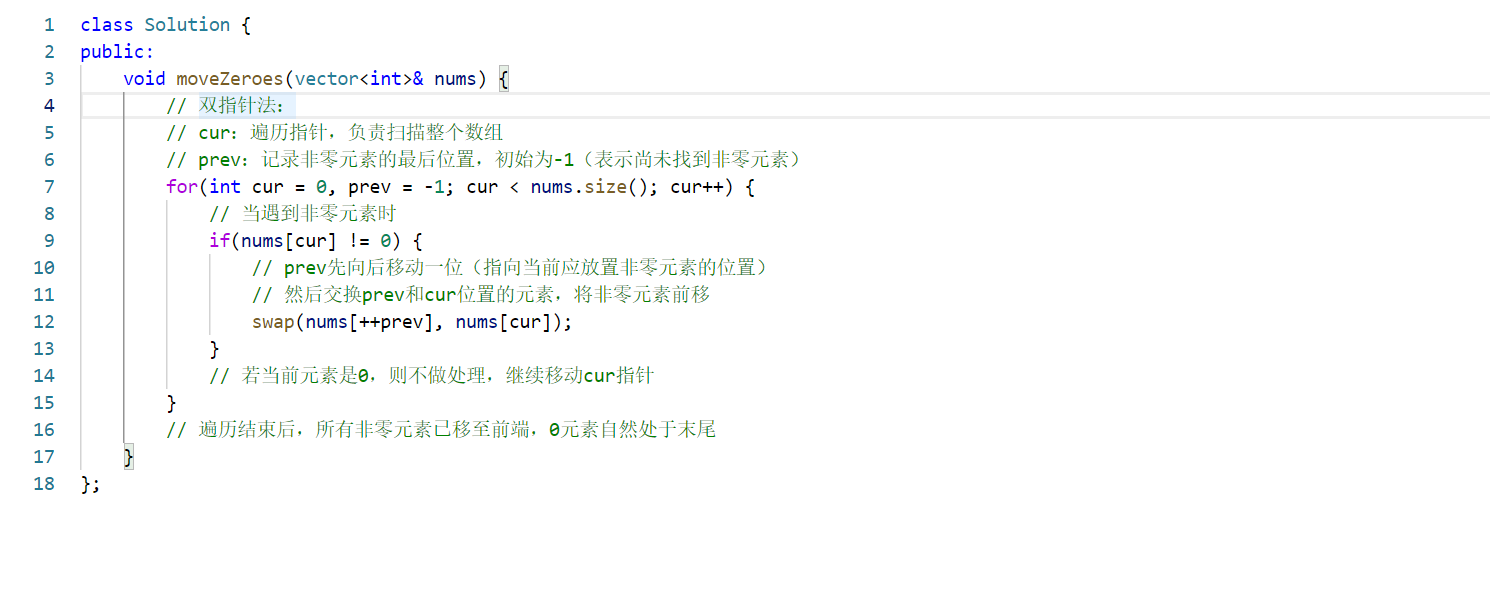
使用双指针法，通过两个指针（prev 和 cur）的配合，高效完成零元素的移动，时间复杂度为 O(n)（n 是数组长度），空间复杂度为 O(1)（仅使用常数级额外空间）。

• cur：遍历指针，负责从头到尾扫描整个数组。
• prev：记录非零元素的「待放置位置」，始终指向已处理部分的最后一个非零元素（初始化为 -1，表示尚未遇到非零元素）。

代码执行步骤

1. 初始化指针：cur = 0（从数组第一个元素开始遍历），prev = -1（初始无有效非零元素）。
2. 遍历数组：cur 从 0 到 nums.size() - 1 逐个移动：
   • 若 nums[cur] 是非零元素（if(nums[cur])，等价于 if(nums[cur] != 0)）：
     • 先将 prev 向前移动一位（++prev），此时 prev 指向「下一个非零元素的放置位置」。
     • 交换 nums[prev] 和 nums[cur]：将当前非零元素 nums[cur] 放到 prev 位置，而原 prev 位置的元素（可能是零，也可能是之前未处理的非零元素）被交换到 cur 位置。
   • 若 nums[cur] 是零元素：不做操作，cur 继续向后移动。
3. 遍历结束：所有非零元素已通过交换移动到数组前端，且保持相对顺序；零元素自然被「挤到」数组末尾。

示例演示

以数组 nums = [0, 1, 0, 3, 12] 为例，模拟执行过程：

步骤 cur nums[cur] prev 操作（交换后数组） 1 0 0 -1 不操作，cur++ 2 1 1（非零） -1 → 0 交换 nums [0] 和 nums [1] → [1,0,0,3,12] 3 2 0 0 不操作，cur++ 4 3 3（非零） 0 → 1 交换 nums [1] 和 nums [3] → [1,3,0,0,12] 5 4 12（非零） 1 → 2 交换 nums [2] 和 nums [4] → [1,3,12,0,0]

最终结果：[1, 3, 12, 0, 0]，符合预期。 

关键细节

• 非零元素相对顺序不变：由于 cur 按顺序遍历，且每次交换都是将「当前非零元素」放到「前一个非零元素的下一位」，因此非零元素的相对顺序不会被破坏。
• 交换的意义：当 prev 和 cur 不相等时，交换会将非零元素前移；当 prev == cur（如数组开头就是非零元素），交换相当于无操作，不影响结果。

 完整代码：