力扣--不同路径、不同路径2、解码方法、使用最小花费爬楼梯

力扣算法题：62. 不同路径 \\ 63.不同路径2 \\ 91.解码方法 \\ 746. 使用最小花费爬楼梯

• 1.不同路径
• • 1.1.状态表示
  • 1.2.状态转移方程
  • 1.3.初始化
  • 1.4.填表顺序
  • 1.5.返回值
  • 1.6.代码
• 2.不同路径2
• • 2.1.状态表示
  • 2.2.状态转移方程
  • 2.3.初始化
  • 2.4.填表顺序
  • 2.5.返回值
  • 2.6.代码
• 3.解码方法
• • 3.1.状态表示
  • 3.2.状态转移方程
  • 3.3.初始化
  • 3.4.填表顺序
  • 3.5.返回值
  • 3.6.代码
• 4.使用最小花费爬楼梯
• • 4.1.状态表示
  • 4.2.状态转移方程
  • 4.3.初始化
  • 4.4.填表顺序
  • 4.5.返回值
  • 4.6.代码

1.不同路径

链接：https://leetcode.cn/problems/unique-paths/description/

1.1.状态表示

dp[i][j]表示从起始点到下标x=i,y=j位置的总路径数

• 如果是初始化，起始点为dp[0][0]
• 如果是虚拟节点，起始点为dp[1][1]

1.2.状态转移方程

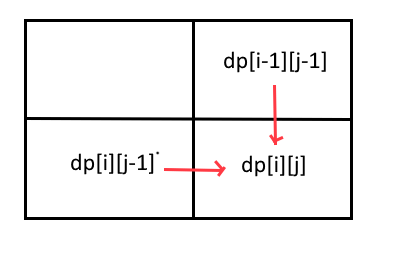
由图知：dp[i][j]的路径总数等于dp[i-1][j]+dp[i][j-1]

1.3.初始化

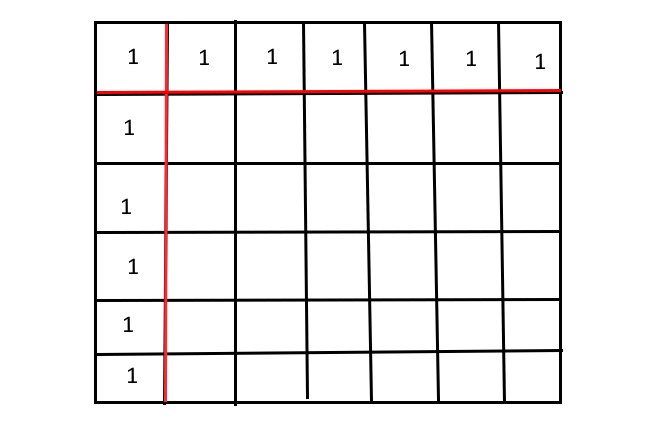
为了防止边缘的元素在赋值是越界，就要这样设置初始值使得dp[i][j]的路径总数等于dp[i-1][j]+dp[i][j-1]合法

使用虚拟节点，可以不对上述有具体含义的dp元素进行初始化，如下：

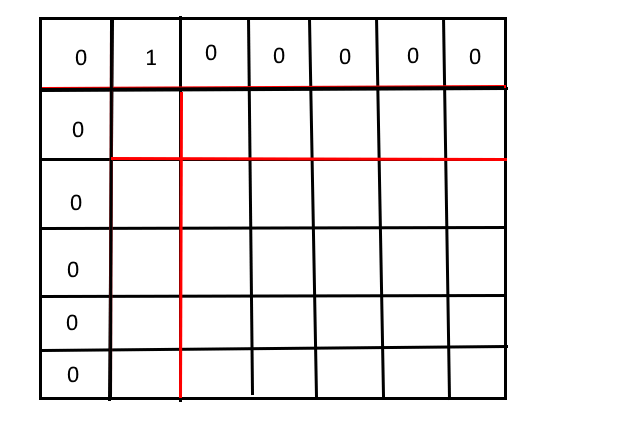
根据设置好的没有如何含义的虚拟节点后，根据填表顺序进行赋值，也能得到和初始化一样的效果dsd

1.4.填表顺序

从上往下，从左往右

1.5.返回值

• 如果是用的初始化，返回dp[m-1][n-1]
• 如果是用的虚拟节点，多出了第一行和第一列，则返回dp[m][n];

1.6.代码

class Solution { public int uniquePaths(int m, int n) { //加入虚拟节点，所以多加一行和一列 int[][] dp = new int[m+1][n+1]; //设置虚拟节点 for(int i = 0;i<=n;i++){ dp[0][i] = 0; } dp[0][1] = 1; for(int j = 0;j<=m;j++){ dp[j][0] = 0; } //根据虚拟节点进行赋值 for(int i = 1;i <= m;i++){ for(int j = 1;j <= n;j++){ dp[i][j] = dp[i][j-1] + dp[i-1][j]; } } return dp[m][n]; }}

2.不同路径2

链接：https://leetcode.cn/problems/unique-paths-ii/submissions/640586583/

2.1.状态表示

dp[i][j]表示从起始点到下标x=i,y=j位置的总路径数

2.2.状态转移方程

如果当前位置是障碍物，则总路径数为0，否则dp[i][j]=dp[i-1][j]+dp[i][j-1]

2.3.初始化

设置虚拟节点，保证在初始位置时的总路径数为1

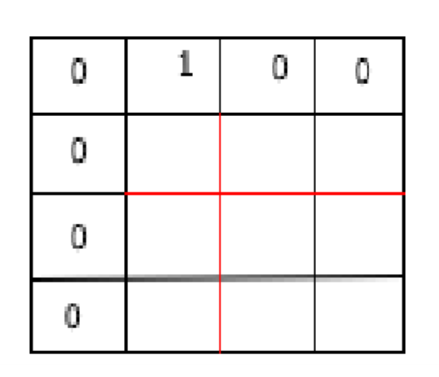
2.4.填表顺序

从上往下，从左往右

2.5.返回值

返回dp[m][n]

2.6.代码

class Solution { public int uniquePathsWithObstacles(int[][] obstacleGrid) { int m = obstacleGrid.length; int n = obstacleGrid[0].length; //要加入虚拟节点，所以加一行和一列 int[][] dp = new int[m + 1][n + 1]; //设置虚拟节点 for (int j = 0; j <= n; j++) { dp[0][j] = 0; } dp[0][1] = 1; for (int i = 0; i <= m; i++) { dp[i][0] = 0; } //对dp表赋值 for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) { //加了一行和一列，取原数组元素时就要-1 //当前位置是障碍物 if (obstacleGrid[i - 1][j - 1] == 0) {  dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; } //当前位置不是障碍物 else {  dp[i][j] = 0; } } } return dp[m][n]; }}

3.解码方法

链接：https://leetcode.cn/problems/decode-ways/description/

3.1.状态表示

dp[i]表示当前i下标所处位置的部分字符串的解码方式总数

3.2.状态转移方程

如图，当i位置的字符不为’0’时,i位置的解码总数要加上i-1位置的解码总数，即dp[i]=0+dp[i-1]；当i-1位置的字符不为’0’,并且i-1位置和i位置的字符所构成的数大于等于10并且小于等于26时，编码合法,i位置的解码总数还要加上i-2位置的解码总数，即dp[i] = dp[i]+dp[i-2];

3.3.初始化

因为求dp[i],要已知dp[i-1]和dp[i-2]才行，所以刚开始要初始化dp[0]和dp[1];
对dp[0]进行初始化：如果str[0]不为’0’,dp[0]=1;
对dp[1]进行初始化：如果str[0]不为’0’并且str[1]也不为’0’，dp[1] = 0+1,如果str[0]和str[1]构成的数大于等于10并且小于等于26,dp[1] = dp[1] +1;

设置虚拟节点方法：
将dp[0]设为1，再根据str[0]是否为’0’初始化dp[1],然后按照逻辑填表，就省去了原来对dp[1]的繁琐的初始化过程，至于为什么设置虚拟节点为1，答案是在对dp[2]进行赋值时,如果str[0]和str[1]构成的数大于等于10并且小于等于26时,dp[2]=dp[2]+dp[2-2],在原来的对dp[1]的初始化中dp[1] = dp[1]+1,所以得到dp[0]要设为1.

3.4.填表顺序

从左向右填表

3.5.返回值

返回最后一个dp元素

3.6.代码

 //解码方法 public int numDecodings(String s) { int n = s.length(); char[] str = s.toCharArray(); //new出来的dp[i]默认是0 int[] dp = new int[n+1]; //设置虚拟节点dp[0]为1 dp[0] = 1; //初始化dp[0] if(str[1-1] != \'0\') dp[1] = 1; for(int i = 2;i <= n;i++){ if(str[i-1] != \'0\'){ dp[i] += dp[i-1]; } int t = (str[i-1-1] - \'0\')*10 + (str[i-1] - \'0\'); if(10 <= t && t <= 26){ dp[i] += dp[i-2]; } } return dp[n]; }

4.使用最小花费爬楼梯

链接：https://leetcode.cn/problems/min-cost-climbing-stairs/description/
有两种方法：一种是dp[i]表示走到当前楼层最少花费的钱；一种是dp[i]表示从从当前位置到终点所要花费的最少钱

4.1.状态表示

方法一： dp[i]表示走到当前楼层最少花费的钱
方法二： dp[i]表示从从当前位置到终点所要花费的最少钱

4.2.状态转移方程

方法一：

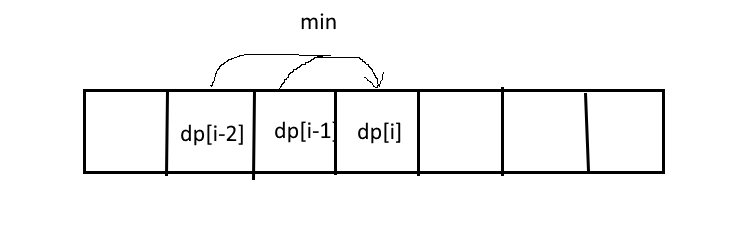
dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);

方法二：

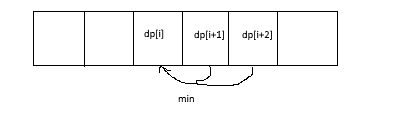
dp[i] = min(dp[i+1]+cost[i],dp[i+2]+cost[i])

4.3.初始化

方法一：
dp[0]和dp[1]为0

方法二：
其中n表示终点楼层
dp[n-1] = cost[n-1];
dp[n-2] = cost[n-2];

4.4.填表顺序

方法一：
从左向右

方法二：
从右向左

4.5.返回值

方法一：
返回dp[n]

方法二：
返回min(dp[0],dp[1])

4.6.代码

方法一：

 //法一:dp[i]表示走到当前楼层最少花费的钱 public int minCostClimbingStairs(int[] cost) { int n = cost.length; int[] dp = new int[n+1]; for(int i = 2;i <= n;i++){ int min = dp[i-2]+cost[i-2]; if(dp[i-1]+cost[i-1] < min) min = dp[i-1]+cost[i-1]; dp[i] = min; } return dp[n]; }

方法二:

 //法二:dp[i]表示从从当前位置到终点所要花费的最少钱 public int minCostClimbingStairs1(int[] cost) { int n = cost.length; int[] dp = new int[n]; //初始化 dp[n-1] = cost[n-1]; dp[n-2] = cost[n-2]; for(int i = n-3;i >= 0;i--){ int min = dp[i+1]; if(dp[i+2] < min) min = dp[i+2]; dp[i] = min+cost[i]; } if(dp[0] < dp[1]){ return dp[0]; }else{ return dp[1]; } }