【数学建模|Matlab】数学建模「常用作图」示例

- 第 117 篇 -
Date: 2025 - 07 - 25
Author: 郑龙浩（仟墨）

Matlab 数学建模 常用作图示例

学习的网课的链接：

文章目录

• Matlab 数学建模 常用作图示例
• 一 二维曲线
• • 1 多图叠加命令
  • 2 具体案例
• 二 二维散点图
• 三 二维渐变图
• • 1 scatter 怎么用
  • 2 实际运用
• 四 条形图
• • 1 方法1 所有柱子一起绘制，最后改色
  • 2 方法2 黑白灰三种柱子分开绘制
• 五 填充图
• • 1 代码解释
  • 2 **如何理解**：
  • 3 实现
• 六 双y轴图
• 七 二维场图
• 八 三维螺旋线图
• 九 三维三点图
• 十 3D伪彩图
• 十一 裁剪伪彩图
• 十二 等高线图
• 十三 3D等高线图
• 十四 等高线填充图
• 十五 3D矢量场图
• 十六 伪彩图 + 投影图
• 十七 热图
• 十八 分子模型图
• 十九 分形图

一 二维曲线

1 多图叠加命令

注意： 只需写一次：绘制多个图时，只需在第一个图之后写一次 hold on，后续所有图自动叠加。

切忌：想要叠加，在每个绘制的图后都写plot

不要这样

2 具体案例

x = linspace(1, 200, 100); % 1 到 200 之间生成 ​​100 个等间距的数​y1 = log(x) + 1; % 第一个函数log(x) + 1 y2 = log(x) + 2; % 第二个函数log(x) + 2y3 = 0.5 * log(x);figure; % 创建画布plot(x, y1); % 图像1hold on % ​​命令：开启图形叠加模式->让多个图绘制在同一个窗口上，避免覆盖之前的图形plot(x, y2, \'LineWidth\', 3); % 图像2，线宽为2plot(x, y3, \'--\', \'LineWidth\', 3); % 线宽5 + 虚线hold off % 命令：关闭图形叠加模式legend(\'y1\', \'y2\', \'y3\'); % 生成图例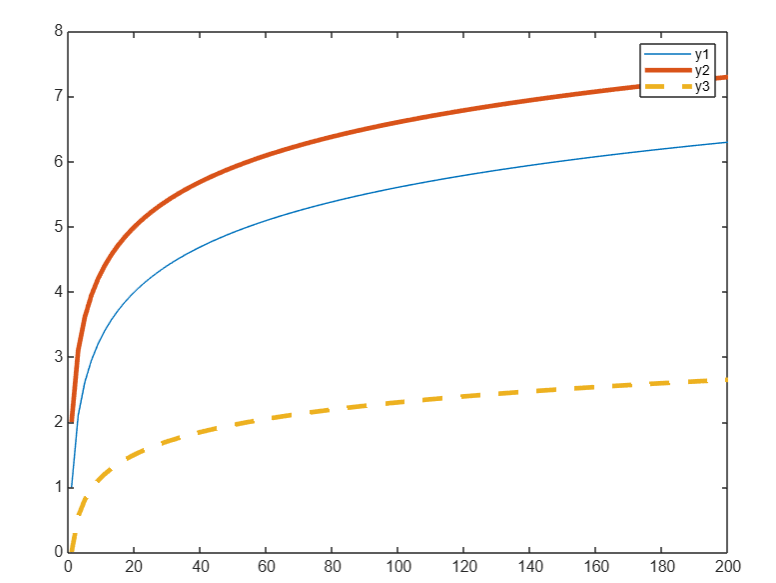

二 二维散点图

figure; % 创建画布x = linspace(1, 200, 100); % 1 到 200 之间生成 ​​100 个等间距的数% y: log(x)所有点y值 + 100个0到1之间的随机数y = log(x);y2 = y + rand(1, 100);% 绘制 log(x) -> 线宽1 + 线条颜色设置黑色plot(x, y, \'LineWidth\', 1, \'Color\', \'k\')hold on % 开启叠加模式% 绘制图像 -> 线宽2 + 标点内部红 + 标点边框里蓝(默认空白)plot(x, y2, \'o\', \'LineWidth\', 2, \'MarkerFaceColor\', \'r\', \'MarkerEdgeColor\', \'b\');hold off % 关闭叠加模式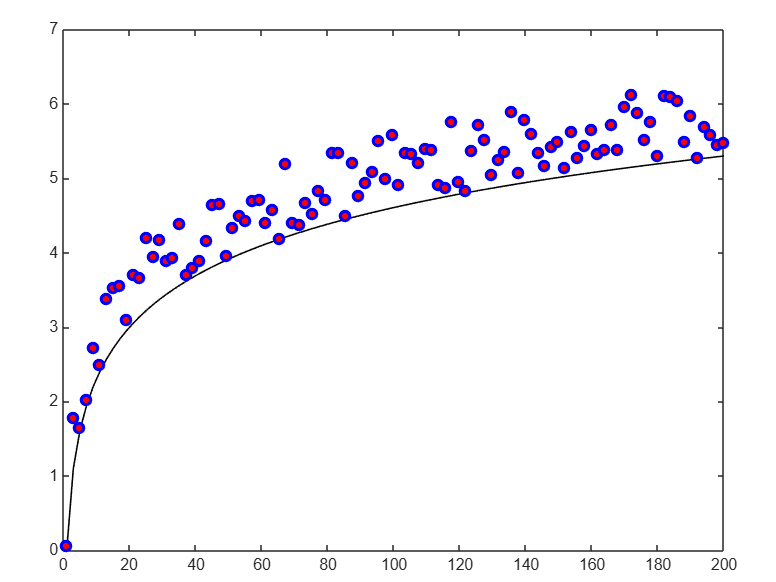

三 二维渐变图

1 scatter 怎么用

• 在向量 x 和 y 指定的位置创建一个包含原型标记的散点图
• 向量x 与 向量y 必须是等长的
• 要在同一组坐标区上绘制多组坐标的话，x 或 y 中至少一个是矩阵
• scatter(x, y, size) 设置圆大小。对所有圆点的大小都设置为 size，如果想绘制不同大小的圆点，将size设置为长度与x/y相同的向量
• scatter(x, y, size, color) 设置圆的颜色。可以为所有圆设置一种颜色，也可以为每个圆设置不同颜色（color需为长度与x/y相同的向量或N×3矩阵）
• scatter(x, y, size, color, \'filled\') 将圆点填充。如果不设置filled的话，生成的点不是实心圆点，而是空心圆点

1. 数值向量 c 通过当前色图自动映射为 RGB 颜色
2. 映射规则：
   min© → 色图的第一个颜色（左端）
   max© → 色图的最后一个颜色（右端）
   中间值 → 线性插值到色图的过渡颜色
3. 注意：映射前会对 c 自动归一化到 [0,1] 区间，也就是实际上看起来范围是1到10，实际上还是0到1

2 实际运用

x = linspace(0, 2*pi, 200); % 范围0 到 2*pi, 200个y = sin(x) + 0.5*rand(1, 200); % 随机生成1行20列的随机数，200个，*0.5是让数幅度大color = linspace(1, 10, length(x)); % 生成和x同等数量的数，第一个1，最后一个10scatter(x, y, 25, color, \'filled\'); % 25 是标点大小，color是颜色表，filled是将标点中间填充

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

四 条形图

有两种方法

1 方法1 所有柱子一起绘制，最后改色

将多个一维向量组合成多维矩阵，然后直接绘图

%% 4 二维条形图 - 方法1% 4 条形图figure;GMM_orders = [2, 4, 6, 8]; % GMM阶数train_time = [0.5, 1.2, 2.1, 3.8]; % 训练耗时/stest_time = [0.1, 0.3, 0.6, 1.2]; % 测试耗时/stotal_time = train_time + test_time; % 总耗时/s% 绘制分组条形图bar_data = [train_time; test_time; total_time]; % 将3个行向量组合为3*4矩阵h = bar(GMM_orders, bar_data);% 设置柱子颜色（黑、灰、白）set(h(1), \'FaceColor\', [0 0 0]); % 黑色 - 训练耗时set(h(2), \'FaceColor\', [0.7 0.7 0.7]); % 灰色 - 测试耗时set(h(3), \'FaceColor\', [1 1 1]); % 白色 - 总耗时% 坐标轴标签xlabel(\'GMM阶数\');ylabel(\'耗时/s\');set(gca, \'XTickLabel\', {\'8阶\', \'16阶\', \'32阶\', \'64阶\'} ); % 句柄就是MATLAB中用来操控图形对象（如坐标轴、线条等）的\"遥控器\"，通过它可以直接修改对象的属性（如文字、颜色、范围等）。% 添加图例legend({\'训练耗时\', \'测试耗时\', \'总耗时\'}, \'Location\', \'northwest\');%%

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

2 方法2 黑白灰三种柱子分开绘制

%% 4 二维条形图 - 方法2% 不喜欢用这方法， 因为柱子位置是手动，上一个办法可以自动选% 4 条形图figure;train_time = [0.5, 1.2, 2.1, 3.8]; % 训练耗时/stest_time = [0.1, 0.3, 0.6, 1.2]; % 测试耗时/stotal_time = train_time + test_time; % 总耗时/s% 绘制分组条形图 颜色主子: 黑 灰 白% 注意：% a:b:c --> a 是起始值，b是步长值，c是结束值bar(2:5:17, train_time, \'BarWidth\', 0.2, \'FaceColor\', [0, 0, 0]);hold onbar(3:5:18, test_time, \'BarWidth\', 0.2, \'FaceColor\', [0.7 0.7 0.7]);bar(4:5:19, total_time, \'BarWidth\', 0.2, \'FaceColor\', [1 1 1]);hold off% 坐标轴标签xlabel(\'GMM阶数\');ylabel(\'耗时/s\');% 增加每个柱子的名字 (gca 是个函数， 返回当前坐标轴的句柄) set(gca, \'XTickLabel\', {\'8阶\', \'16阶\', \'32阶\', \'64阶\'} ); % 句柄就是MATLAB中用来操控图形对象（如坐标轴、线条等）的\"遥控器\"，通过它可以直接修改对象的属性（如文字、颜色、范围等）。% 添加图例legend({\'训练耗时\', \'测试耗时\', \'总耗时\'}, \'Location\', \'northwest\');%%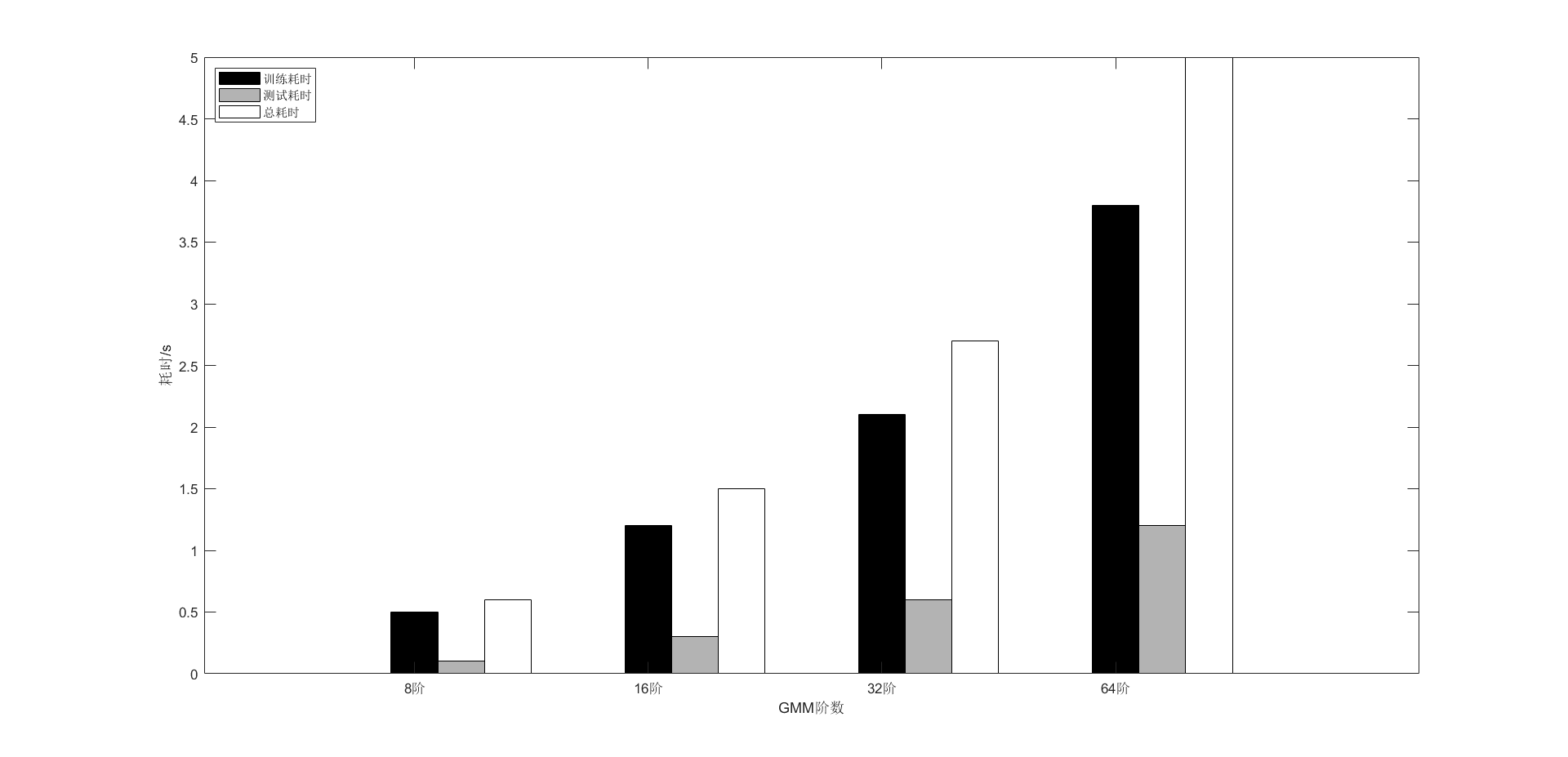

五 填充图

1 代码解释

• max 与 min

  当max 与 min函数中的内容是一维数据的时候，得出是最大最小值，当是多维数据的时候，默认得出的是每一列的最大值，并且存到一个一维数据当中

• [y1, y2]：两个向量组合成二维数据

• fliplr(x) 比如将 [1, 2, 3, 4, 5] 变为 [5, 4, 3, 2, 1]

• % 创作一个需要填充的图像的边的坐标x的值，先从左往右，再从右往左，存入同一个向量xFill = [x, fliplr(x)];% 创作一个需要填充的图像的边的坐标y的值，先从左往右，再从右往左，存入同一个向量yFill = [maxY, fliplr(minY)];

  为什么需要这样构造？

  因为 fill 函数需要一组闭合的(x,y)坐标来定义填充区域。通过：

  • 正向的x和上边界maxY定义上部曲线
  • 反向的x和下边界minY定义下部曲线
    这样组合就形成了一个完整的闭合多边形，可以正确填充两条曲线之间的区域。

2 如何理解：

想象用笔描绘这个区域：

1. 从左端点开始，沿上边界画到右端点
2. 然后从右端点开始，沿下边界画回左端点
3. 这样就完成了一个闭合图形的描绘

3 实现

x = 0:0.01:2*pi;y1 = sin(2*x);y2 = sin(x);% 计算两条曲线在每个x点的上下边界(max/min)% [y1; y2]将两个行向量垂直堆叠成一个两行的矩阵，相当于把两条曲线的数据上下组合起来% max(二维矩阵) max 函数对二维矩阵默认按列操作 -> 每列最大maxY = max([y1; y2]); % 表示在每个x位置上两个函数中的最大值（上边界）minY = min([y1; y2]); % 表示在每个x位置上两个函数中的最小值（下边界）% 创作一个需要填充的图像的边的坐标x的值，先从左往右，再从右往左，存入同一个向量xFill = [x, fliplr(x)];% 创作一个需要填充的图像的边的坐标y的值，先从左往右，再从右往左，存入同一个向量yFill = [maxY, fliplr(minY)];% 绘图figure % 画布fill(xFill, yFill, \'g\') % 函数内容填充绿色hold on % 开启叠加plot(x, y1, \'k\', \'LineWidth\', 2); % 描边plot(x, y2, \'k\', \'LineWidth\', 2); % 描边hold off % 关闭叠加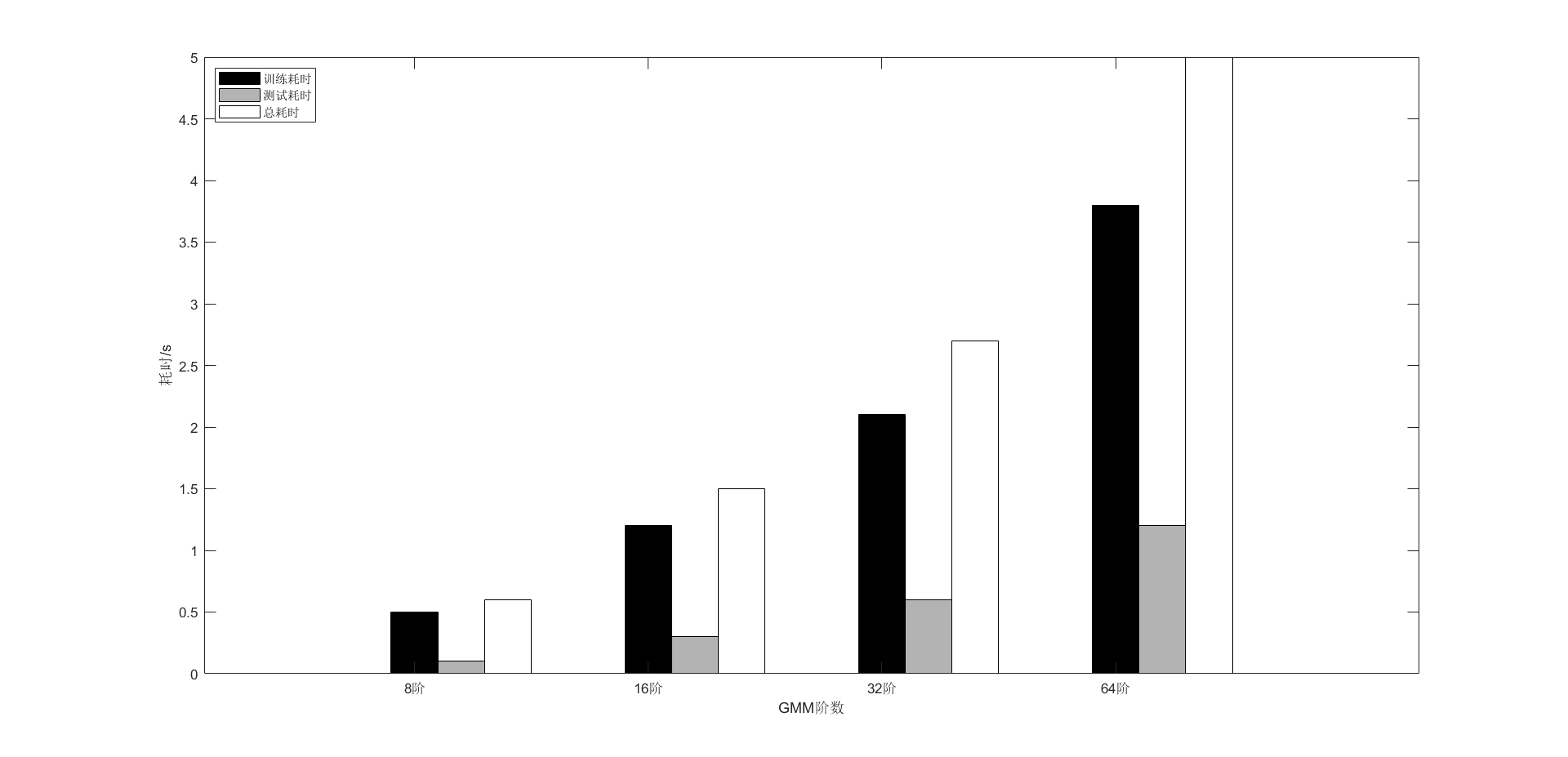

六 双y轴图

就是一个窗口内有不同y轴的图像，这俩y轴的范围是不同的

x = 0:0.1:10;y1 = sin(x); % 第一条曲线y2 = sin(x - 1); % 第二条曲线% 创建画布figure;% 第一个 y 轴（左侧）yyaxis left; % 激活左侧 y 轴plot(x, y1, \'b-\', \'LineWidth\', 2); % 绘制 y1（蓝色实线）ylabel(\'y1 = sin(x)\'); % 左侧 y 轴标签ylim([-1.5 1.5]); % 设置左侧 y 轴范围% 第二个 y 轴（右侧）yyaxis right; % 激活右侧 y 轴plot(x, y2, \'r--\', \'LineWidth\', 2); % 绘制 y2（红色虚线）ylabel(\'y2 = sin(x - 1)\'); % 右侧 y 轴标签ylim([-3.5, 3.5]); % 设置右侧 y 轴范围% 公共设置xlabel(\'x\'); % x 轴标签title(\'双 y 轴示例图\'); % 标题grid on; % 显示网格legend(\'y1 (左轴)\', \'y2 (右轴)\'); % 图例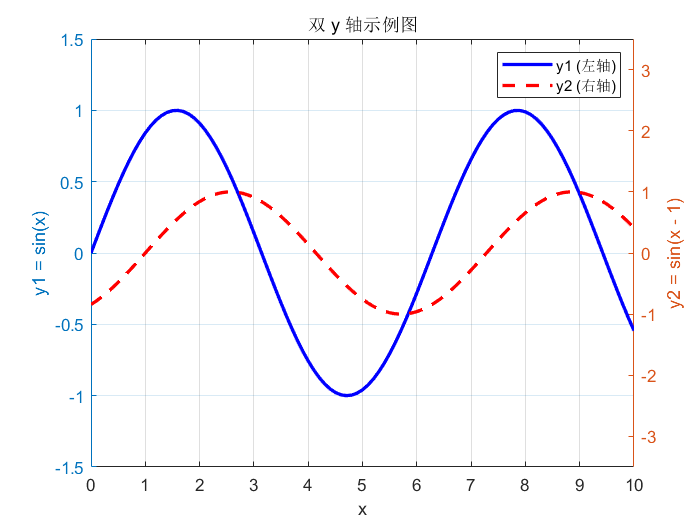

七 二维场图

% 创建二维网格坐标（范围0到1，步长0.1）[x, y] = meshgrid(0:0.1:1, 0:0.1:1);% 定义x方向的速度分量（与x坐标成正比）u = x; % 速度u = x，表示向右的速度随x增大而增大% 定义y方向的速度分量（与y坐标成反比，负号表示向下）v = -y; % 速度v = -y，表示向下的速度随y增大而增大% 设置流线起始点的x坐标（从0.1到0.9，间隔0.1）startx = 0.1:0.1:0.9; % 在x轴上均匀分布的9个起始点% 设置流线起始点的y坐标（全部固定在y=1的位置）starty = ones(size(startx)); % 所有起始点的y坐标均为1% 创建新的图形窗口figure; % 绘制矢量场箭头：用箭头表示每个网格点处的速度向量(u,v)quiver(x, y, u, v); % quiver函数显示速度场，箭头方向表示向量方向，长度表示大小% 绘制流线：从指定起始点(startx,starty)开始追踪速度场生成的流线streamline(x, y, u, v, startx, starty);% streamline函数会沿着速度场(u,v)的方向生成连续的流线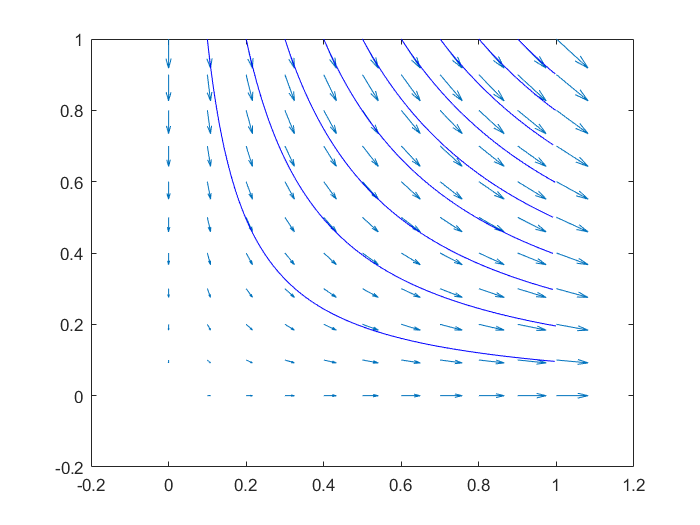

八 三维螺旋线图

t = 0:0.1:10*pi; % 参数 tx = sin(t);y = cos(t);z = t;plot3(x, y, z, \'b:\', \'LineWidth\', 1.5);xlabel(\'X\'); ylabel(\'Y\'); zlabel(\'Z\');title(\'3D 螺旋线图\');grid on;view(30, 30); % 调整视角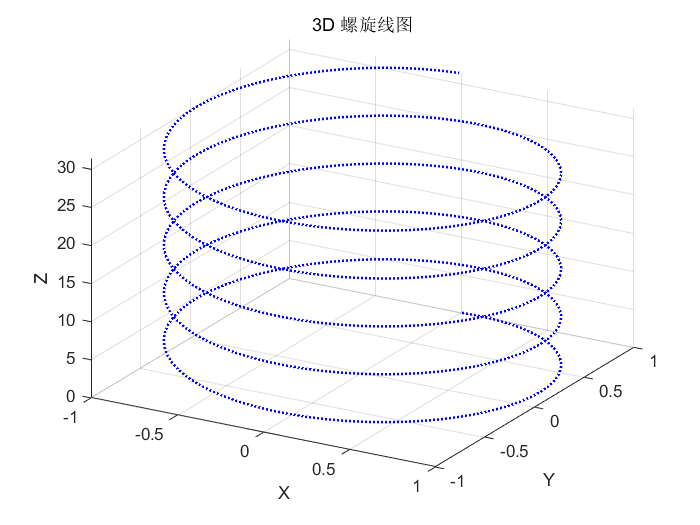

九 三维三点图

• sphere(n) 生成一个由 n * n的网格点组成的球面，可以理解为

  • 把地球的经线和纬线各分成 n 等份，交叉形成 n * n 个小格子（50行×50列）
  • 每个格子角上的点连起来，拼出一个“看起来光滑”的球
  • 比如是15的时候略显棱角，50的时候就很光滑
  • 返回的内容是 n * n 个点坐标

• numel(矩阵) 返回这个矩阵中的元素数量

  numel([1, 2, 3; 4, 5, 6; 7, 8, 9])% 结果是9

• repmat()来重复复制数组或矩阵的函数，能按行、列或更高维度堆叠出更大的新数组

  A = repmat(5, 2, 3); % 复制数字5，生成 2 行 3 列矩阵、A = 5 5 5 5 5 5

figure;[X,Y,Z] = sphere(50); % 生成 50 * 50 个点的坐标% 将大球拆分成三个大小不同的球体x = [0.5*X(:); 0.75*X(:); X(:)]; % 三层球面的 x 坐标（半径 0.5, 0.75, 1）y = [0.5*Y(:); 0.75*Y(:); Y(:)]; % 三层球面的 y 坐标z = [0.5*Z(:); 0.75*Z(:); Z(:)]; % 三层球面的 z 坐标S = repmat([10, 5, 2],numel(X), 1); % numel(X)得出50，生成50行[70,50,20]C = repmat([1, 2, 3], numel(X), 1); % 颜色size = S(:); % 将S按照列优先展开 --> 3 * 50 -> 150* 1color = C(:); % 同上h = scatter3(x, y, z, size, color);h.MarkerFaceColor = \'g\'; % 将空心填上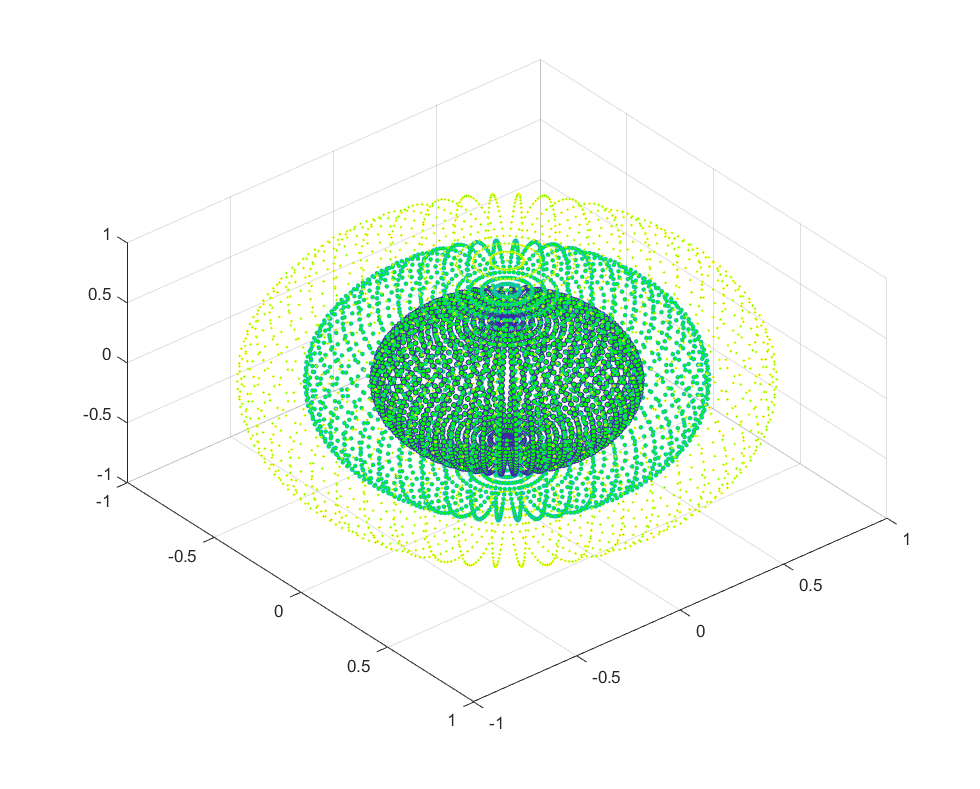

x = linspace(1, 200, 100);y1 = log(x) + 1;y2 = log(x) + 2;y3 = y1 + rand(1, 100) - 0.5;figurescatter3(x, y2, y3, x, x, \'filled\');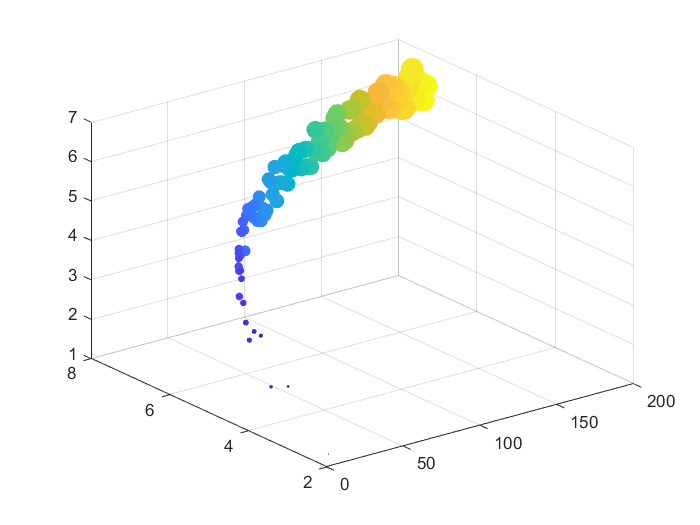

十 3D伪彩图

[x, y, z] = peaks(30);figure;plot1 = subplot(1,2,1); % subplot指的是图像的位置1 2 1 --> 1行2列第1个surf(x, y, z); % 绘制三维曲面图title(\'左图（默认配色）\');plot2 = subplot(1,2,2); % 图像位置 1 2 2 --> 1行2列第2个surf(x, y, z); % 绘制三维曲面图title(\'右图（热力图配色）\');% 获取当前坐标轴（右图）colormap(gca, hot); % 将当前图形中所有子图的颜色设置为热力图配色（黑→红→黄→白渐变）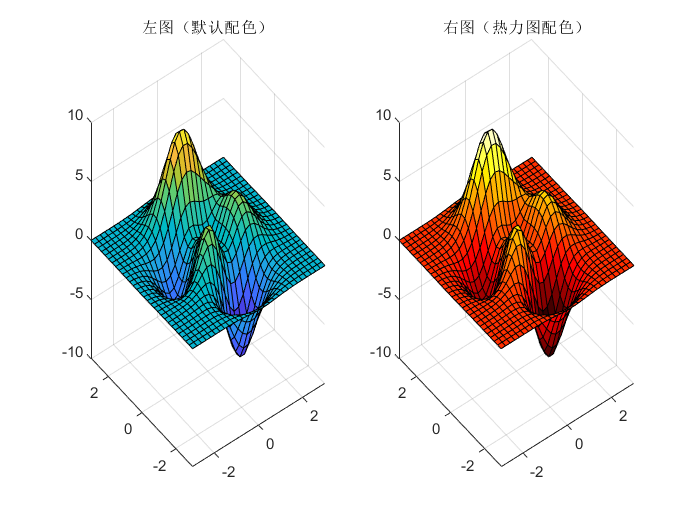

十一 裁剪伪彩图

figure; % 创建新图形窗口n = 300; % 定义网格大小[x, y, z] = peaks(n); % 生成peaks函数的300x300网格数据% 左上子图(占据第1和第3位置)subplot(2, 2, [1,3]) surf(x, y, z); % 绘制完整曲面shading interp % 平滑着色view(0, 90) % 俯视图(0度方位角，90度仰角)% 处理数据：在椭圆环区域将z值设为NaNfor i = 1:n for j = 1:n if x(i, j)^2 + 2 * y(i, j)^2 > 6 && 2 * x(i, j)^2 + y(i, j)^2 < 6 z(i, j) = NaN; % 满足条件设为NaN(不显示) end endend% 右上子图subplot(2, 2, 2)surf(x, y, z); % 绘制处理后的曲面shading interpview(0, 90)% 右下子图subplot(2, 2, 4)surf(x, y, z); % 再次绘制处理后的曲面shading interp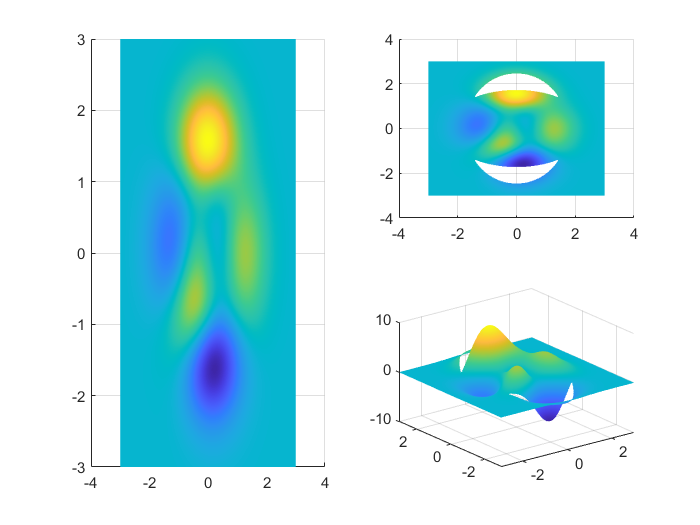

十二 等高线图

figure; % 创建新图形窗口[X, Y, Z] = peaks; % 生成peaks函数数据（标准测试曲面）subplot(2, 2, 1);contour(X, Y, Z, 20, \'LineWidth\', 2); % 绘制20条等高线（显示曲面轮廓）subplot(2, 2, 2);contour(X, Y, Z, \'--\', \'LineWidth\', 2); % 绘制虚线样式的等高线subplot(2, 2, 3);v = [1, 1]; % 指定要显示的等高线值contour(X, Y, Z, v, \'LineWidth\', 2); % 仅绘制Z=1的等高线% 生成新的网格和曲面数据（用于演示不同函数的等高线）x = -2:0.2:2;y = -2:0.2:3;[X, Y] = meshgrid(x, y); % 创建网格坐标Z = X.*exp(-X.^2-Y.^2); % 计算高斯衰减曲面subplot(2, 2, 4);contour(X, Y, Z, \'ShowText\',\'on\', \'LineWidth\', 2); % 绘制带数值标注的等高线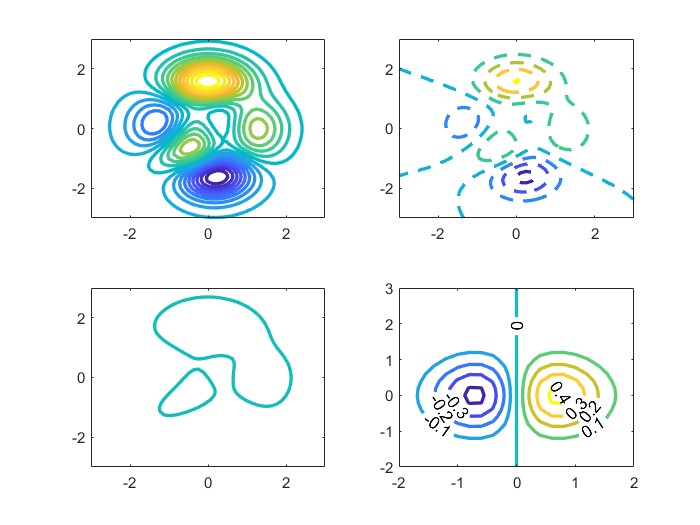

十三 3D等高线图

figure(\'Position\', [0, 0, 900, 400]); % 创建900×400像素的图形窗口% 第一个子图：球体的3D等高线subplot(1, 3, 1); % 创建1行3列的第1个子图[X, Y, Z] = sphere(50); % 生成50×50网格的球面坐标contour3(X, Y, Z, \'LineWidth\', 2); % 绘制3D等高线，线宽为2% 第二个子图：高斯曲面的3D等高线（带数值标注）subplot(1, 3, 2); % 创建第2个子图[X, Y] = meshgrid(-2:0.25:2); % 创建-2到2的0.25间隔网格Z = X.*exp(-X.^2-Y.^2); % 计算高斯衰减曲面contour3(X, Y, Z, [-0.2 -0.1 0.1 0.2], ... % 仅绘制指定值的等高线 \'ShowText\', \'on\', \'LineWidth\', 2) % 显示等高线数值，线宽为2% 第三个子图：peaks函数的3D等高线subplot(1, 3, 3); % 创建第3个子图[X, Y, Z] = peaks; % 生成peaks函数数据contour3(X, Y, Z, [2 2], \'LineWidth\', 2); % 仅绘制Z=2的等高线，线宽为2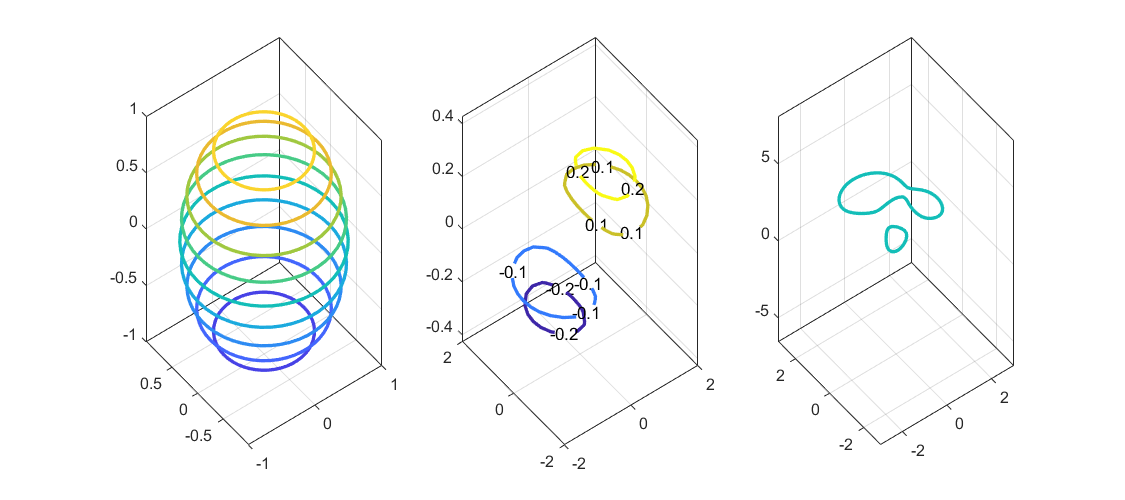

十四 等高线填充图

figure; % 创建新的图形窗口% 第一个子图：基本填充等高线图subplot(2, 2, 1); % 创建2行2列的第1个子图[X, Y, Z] = peaks(50); % 生成50×50的peaks函数数据contourf(X, Y, Z); % 绘制填充等高线图(自动选择等高线)% 第二个子图：虚线样式的填充等高线subplot(2, 2, 2); % 创建第2个子图contourf(X, Y, Z, \'--\'); % 绘制虚线样式的填充等高线% 第三个子图：指定等高线值并显示数值subplot(2, 2, 3); % 创建第3个子图contourf(X, Y, Z, [2 3], \'ShowText\', \'on\'); % 仅绘制Z=2和Z=3的等高线，并显示数值% 第四个子图：单值等高线subplot(2, 2, 4); % 创建第4个子图contourf(X, Y, Z, [2 2]); % 仅绘制Z=2的等高线(单值)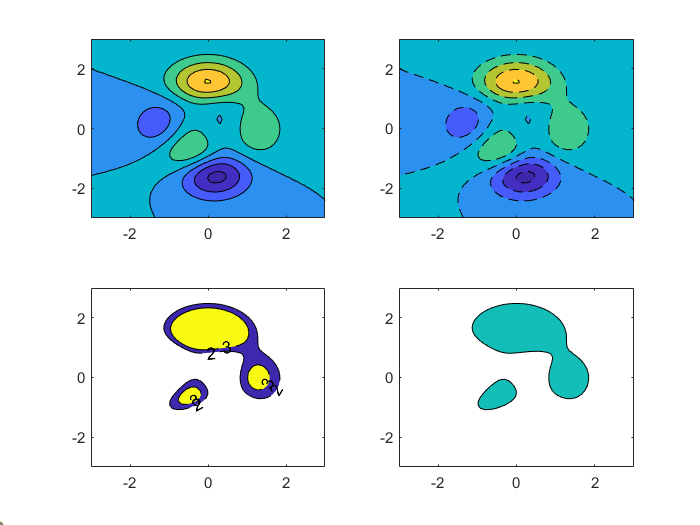

十五 3D矢量场图

figure; % 创建新的图形窗口% 生成peaks函数数据（30x30网格）[X, Y, Z] = peaks(30); % 计算曲面法线向量（U,V,W为法线在各方向的分量）[U, V, W] = surfnorm(X, Y, Z); % 绘制3D矢量场（箭头表示法线方向）% 参数说明：% X,Y,Z - 箭头起点坐标% U,V,W - 箭头方向向量% 0.5 - 箭头长度缩放因子% \'r\' - 箭头颜色（红色）quiver3(X, Y, Z, U, V, W, 0.5, \'r\'); hold on % 保持当前图形，以便叠加绘制% 绘制peaks曲面surf(X,Y,Z); % 设置坐标轴范围xlim([-3, 3]); % x轴范围-3到3ylim([-3, 3.2]); % y轴范围-3到3.2% 平滑着色（消除网格线）shading interphold off % 关闭图形保持% 设置视角（0度方位角，90度仰角 - 俯视图）view(0, 90);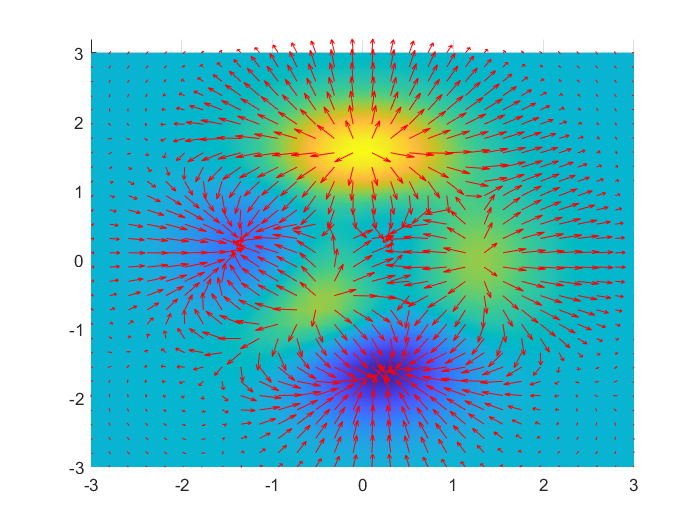

十六 伪彩图 + 投影图

clear; clc; close all; % 清空工作区、命令窗口和所有图形窗口% 生成x和y坐标向量x = linspace(-3, 3, 30); % 在-3到3之间生成30个等间距点y = linspace(-4, 4, 40); % 在-4到4之间生成40个等间距点% 创建网格坐标[X, Y] = meshgrid(x, y); % 生成40×30的网格坐标矩阵% 计算peaks函数值Z = peaks(X, Y); % 生成40×30的peaks函数值矩阵% 将Z矩阵的部分区域设为0Z(5:10, 15:20) = 0; % 将第5-10行、15-20列的元素设为0% 计算每列和每行的最大值z1 = max(Z); % 每列的最大值，得到1×30向量z2 = max(Z, [], 2); % 每行的最大值，得到40×1向量figure; % 创建新的图形窗口% 上方子图：绘制每列最大值曲线subplot(3, 3, [1, 2]); % 占据第1行第1-2列的位置plot(x, z1, \'LineWidth\', 2); % 绘制x-z1曲线，线宽为2% 右侧子图：绘制每行最大值曲线subplot(3, 3, [6, 9]); % 占据第2-3行第3列的位置plot(z2, y, \'LineWidth\', 2); % 绘制z2-y曲线，线宽为2% 主图区域：绘制peaks曲面subplot(3, 3, [4, 5, 7, 8]); % 占据中间区域surf(x, y, Z); % 绘制3D曲面图xlim([-3, 3]); % 设置x轴范围ylim([-4, 4]); % 设置y轴范围view(0, 90); % 设置视角为俯视图(0度方位角，90度仰角)shading interp; % 去除网格线，使用插值着色（更平滑）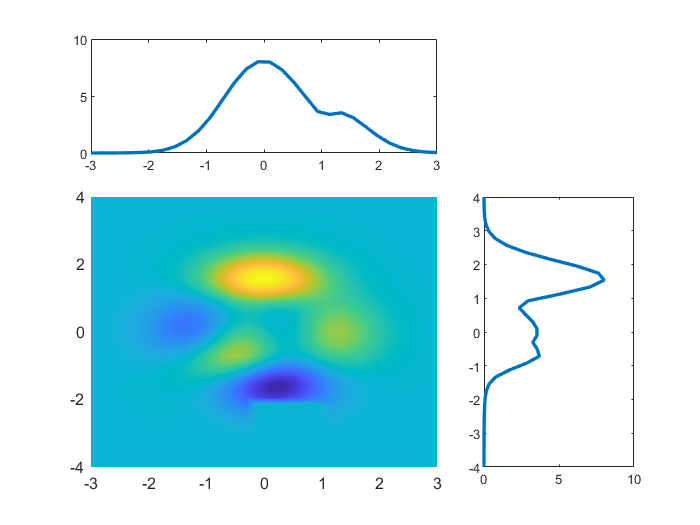

十七 热图

% 生成50x50的随机矩阵（值在0~1之间）z = rand(50); % 将随机值离散化为3个等级z(z >= 0.0 & z < 0.6) = 0.5; % 60%概率设为0.5z(z >= 0.6 & z < 0.8) = 0.7; % 20%概率设为0.7z(z >= 0.8 & z <= 1) = 0.9; % 20%概率设为0.9% 对前30列随机设置NaN（模拟数据缺失）for i = 1:30 z(randi(50, 1, 1) : end, i) = nan; % 从随机行开始设为NaNend% 对后20列设置不同的NaN范围for i = 31:50 z(30 + randi(20, 1, 1) : end, i) = nan; % 从30+随机行开始设为NaNend% 设置特定区域为NaN（模拟异常数据）z(20:25, 40:45) = nan;figure; % 创建新图形窗口% 使用pcolor绘制伪彩色图（比surf更适合2D数据可视化）ax = pcolor(z); % 设置视图为俯视角度（0度方位角，90度仰角）view(0, 90); % 将网格线颜色设为白色（淡化网格线效果）ax.EdgeColor = [1 1 1];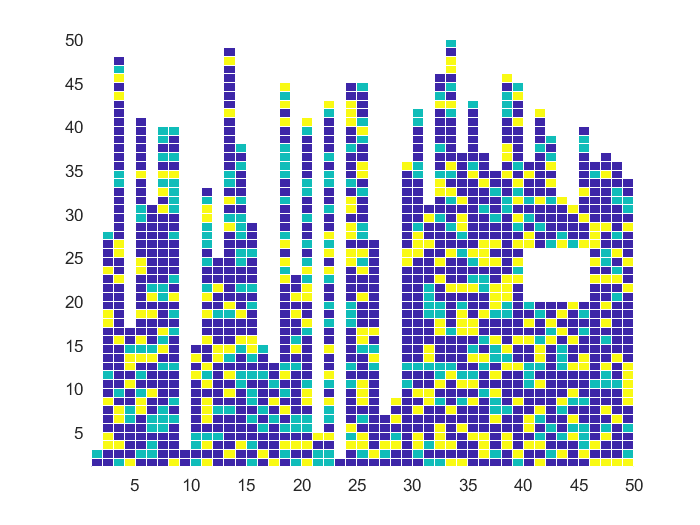 

十八 分子模型图

clear; clc; % 清空工作区和命令窗口% 生成高精度球面坐标（100x100网格）[x, y, z] = sphere(100); % 定义大球和小球的半径C = 10; % 大球半径H = 5; % 小球半径figure; % 创建新图形窗口% 绘制中心大球（红色）surf(C*x, C*y, C*z, \'FaceColor\', \'red\', \'EdgeColor\', \'none\');hold on; % 保持图形，继续绘制% 绘制四个蓝色小球（分布在空间不同位置）surf(H*x, H*y, H*z + 10, \'FaceColor\', \'blue\', \'EdgeColor\', \'none\'); % 上方小球surf(H*x + 10, H*y, H*z - 3, \'FaceColor\', \'blue\', \'EdgeColor\', \'none\'); % 右侧小球surf(H*x - 4, H*y - 10, H*z - 3, \'FaceColor\', \'blue\', \'EdgeColor\', \'none\'); % 左前下方小球surf(H*x - 4, H*y + 10, H*z - 3, \'FaceColor\', \'blue\', \'EdgeColor\', \'none\'); % 右前下方小球% 设置坐标轴属性axis equal; % 保持各轴比例一致axis off; % 隐藏坐标轴% 添加光源增强立体感light;% lighting none; % 如需关闭光照可取消注释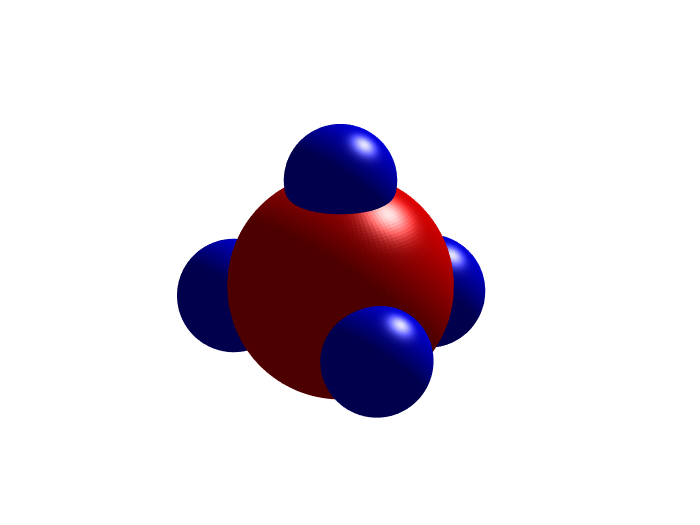

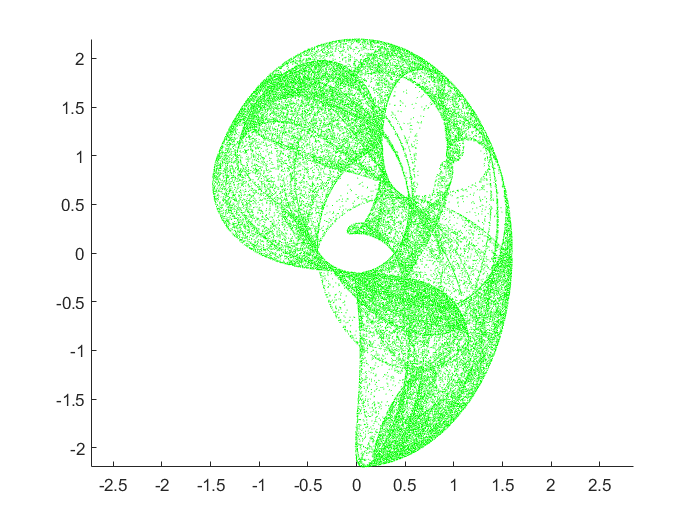
十九 分形图

clear; % 清空工作区变量% 定义非线性映射参数（不同参数会产生不同图案）a = 1.7; b = 1.7; c = 0.6; d = 1.2; % 示例参数组合% 其他可选参数组合：a=1.5; b=-1.8; c=1.6; d=0.9;% 初始化起点坐标x = 0; y = 0;% 设置迭代次数（点数）n = 100000; % 预分配存储数组kx = zeros(1, n); % 存储x坐标ky = zeros(1, n); % 存储y坐标% 迭代生成非线性映射点集for i = 1:n % 非线性变换公式（构成动力系统） tempx = sin(a*y) + c*cos(a*x); % x坐标变换 tempy = sin(b*x) + d*cos(b*y); % y坐标变换 % 存储当前点坐标 kx(i) = tempx; ky(i) = tempy; % 更新迭代变量 x = tempx; y = tempy;end% 绘制散点图（生成分形图案）scatter(kx, ky, 0.1, \'green\'); % 点大小0.1，绿色axis equal; % 保持坐标轴比例一致

职称论文代发