动态规划(3):数位dp与状态压缩dp_dp,dq泄露 如果我们知道了 ,则 的第i位将由 的第i位唯一确认, 也同理,那么对于每
目录
前言
一、数位dp
1.引入
2.数位dp的实现
1)循环递推法
2)记忆化搜索
二、状态压缩dp
1.什么是状压dp
2.如何实现状压dp
三、总结
前言
今天依旧dp,不过今天的再上一层难度!
今天的数位dp和状态压缩dp都与进制有关,单开一列!
一、数位dp
1.引入
引入数位dp之前,我们先来讲数位吧!
对于十进制数而言,数位就是将数以个位、十位、百位之类的去分开,并对每一位求解。
十进制拆开后都是0~9,二进制、三进制同理。
那么数位dp是什么呢?
比如我们要求1~9999里面有多少个数,聪明人一眼就得出来了,笨笨的我只能一个一个计数。
1,2,3,4……1000,1001……1999,2000……2999,3000,3001……诶,数到多少了来着?
不管了,再数一遍吧……
我们发现,在数数的过程中,有很多重复的地方,比如数7000~7999和8000~8999,这些都很相似,唯一的不同就是千位数。如果我们把这些答案存储起来,并用数组表示出来,是否可以用类似于dp的方式转移呢?
当然可以了!恭喜你,发明了数位dp!
2.数位dp的实现
一般的,我们将原本的区间[l,r]转变为[0,r] - [0,l-1]即可。那么,我们就不用考虑左边界了。
1)循环递推法
我们先不讲什么是循环递推法。
以下给出两个例题,借助题目理解一下:
给定两个正整数a,b,求在[a,b]中的所有整数中,每个数码(0~9)各出现了多少次。
其中,1<= a,b <= 1e12。
什么是数码出现的次数?比如,11151222中,5出现了1次,2出现了3次,1出现了4次。
设
表示满 i 位的数中每个数字出现的次数,因为比较复杂,所以我们先不考虑前导零。
偶然发现第 i 位对于每个数字都可能出现一次,也就是说对于所有满 i 位的数的集合,每个数字出现的次数是相同的。
所以状态转移方程为:
。
左边的来自前 i-1 位数字的贡献,右边的是来自第 i 位的数字的贡献。
有了 f 数组,我们来考虑如何统计答案。
首先定义上界表示当前位的最高可取的数。
将上界按位分开,从前往后枚举,当前位的数不贴着上界时,后面可以随便取值。
当前位的数贴着上界时,后面就只能取0~上界,可以分两部分去分别计算贡献。
最后考虑前导0,若第 i 位为前导0时(注意是前导0,前面都是0,并非光自己是0),那么第1到 i-1 位也都是0,也就是多算了将 i-1 位填满的答案,需要额外减去。
代码如下:
ll l,r,f[N],pow10[N],ans1[N],ans2[N],num[N];void solve(ll x,ll *ans){ ll cnt=n,len=0; while(x) num[++len]=x%10,x/=10; //将数x按数位拆分 for(int i=len;i;i--) //由于是将x从后往前拆分,所以从后往前枚举才能得到正确顺序的x { for(int j=0;j<10;j++) ans[j]+=f[i-1]*num[i]; //未达到上限的 for (int j=0;j<num[i];j++) ans[j]+=pow10[i-1]; //达到上限的 cnt-=pow10[i-1]*num[i]; ans[num[i]]+=cnt+1; ans[0]-=pow10[i-1]; //减去前导0的情况 }}int main(){ l=read(),r=read(); pow10[0]=1ll; for(int i=1;i<=13;i++) //根据r的取值范围定 { f[i]=f[i-1]*10+pow10[i-1]; pow10[i]=10ll*pow10[i-1]; } solve(r,ans1),solve(l-1,ans2); //按照[0~r]和[0~l-1]分别求答案 for(int i=0;i<10;i++) cout<<ans1[i]-ans2[i]<<endl; //输出答案:[0~r]-[0~l-1] return 0;}
很明显啊,这道数位dp水的不能再水了。那么接下来,我们来一道稍微难一点的题:
在区间[a,b]中,有多少个不含前导零且相邻两个数字之差大于等于 2 的正整数?
其中,1<= a,b <=1e18
设
表示以数字 x 为开头,往后(往右)长度为 y 的方案数。
枚举 i 为目前长度, j 为当前位的数字,k 为右边位的数字,很容易得到状态转移方程:
=2} f[j][i]+=f[k][i-1]\" class=\"mathcode\" src=\"https://latex.csdn.net/eq?_%7Bj%3D0-9%2Ck%3D0-9%7D%5E%7Babs%28j-k%29%3E%3D2%7D%20f%5Bj%5D%5Bi%5D+%3Df%5Bk%5D%5Bi-1%5D\" />,不再证明。
接下来重点考虑如何统计答案。
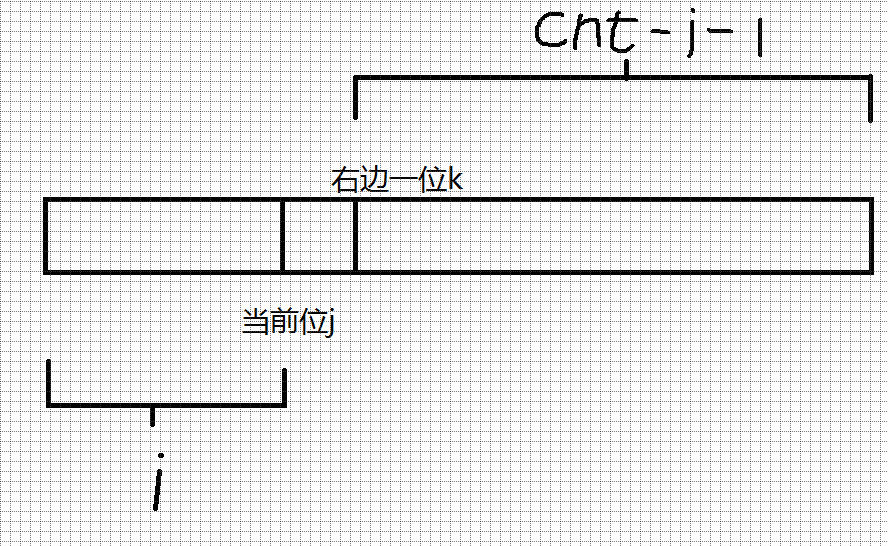
借鉴上一题做法,具体细节看代码,这里只讲解ans+=f[k][cnt-i-1],如图:
ll a,b,f[20][20],num[20];ll solve(ll x){memset(num,0,sizeof(num));ll cnt=0,ans=0;while(x) num[cnt++]=x%10,x/=10; //依旧把x拆分reverse(num,num+cnt); //这里翻转num数组,便于之后的递推 //对于长度与x相等的数,进行特殊求解(因为需要考虑上限和前导0)for(int i=0;i<cnt;i++) //递推每一位for(int j=(i==0?1:0);j<num[i];j++) //枚举第i位是数字j,特判第一位不能为0{bool flag=1;for(int k=1;k<i;k++) if(abs(num[k]-num[k-1])<2) flag=0; //判断之前的数是否符合题目条件if(i&&abs(num[i-1]-j)<2) flag=0; //判断这一位枚举的j是否符合题目条件if(flag){if(i==cnt-1) ans++; //特判,如果是最后一位,那么一定是一个答案else for(int k=0;k=2) ans+=f[k][cnt-i-1]; //枚举右边一位是数字k,判断是否符合题目条件并更新答案}} //对于与数字x长度不一样的,直接更新答案for(int i=1;i<cnt;i++) for(int j=1;j<=9;j++) ans+=f[j][i];return ans;}int main(){for(int i=0;i<=9;i++) f[i][1]=1; //特判数字0~9for(int i=2;i<=20;i++) //根据a,b的范围,最大1e18for(int j=0;j<=9;j++) //枚举当前位是数字jfor(int k=0;k=2)f[j][i]+=f[k][i-1]; //判断是否符合题目条件,并状态转移a=read(),b=read();cout<<solve(b+1)-solve(a)<<endl; //由于solve只能求出小于自己的答案,所以应该这样return 0;}
这就是循环递推法,预处理出dp数组,并在统计答案时利用循环往后递推。
但是,数位dp根本没有这么简单,你永远想象不到会出什么样的恶心题目让你求状态转移方程。
因此,前辈们给出了更简单更模板的方法!
2)记忆化搜索
没错!记忆化搜索!
还是以上一题为例,只要写一道就够了。
具体见代码:
int a,b,num[20],cnt,f[20][20][2][2],ans1,ans2;int dfs(int pos,int pre,bool zero,bool limit)//pos是当前搜索到第几位,pre是上一位选择谁,zero表示之前的是否全为0,limit表示之前的是否都达到上限{if(pos>=cnt) return !zero; //搜索结束后,如果前面全为0,则不是一种答案,否则是一种答案if(f[pos][pre][zero][limit]!=0xefefefef) return f[pos][pre][zero][limit]; //记忆化int maxn=(limit?num[pos]:9),ans=0; //如果之前都达到上限,这一位最多不能超过num[pos]for(int i=0;i=2) //要么前面全为0,要么满足题目要求ans+=dfs(pos+1,i,zero&&(i==0),limit&&(i==maxn));return f[pos][pre][zero][limit]=ans; //记忆化}int main(){a=read()-1,b=read(),cnt=0; //由于dfs求得的是小于等于x的答案,所以a读入时减一memset(f,0xef,sizeof(f));while(b) num[cnt++]=b%10,b/=10; //拆分reverse(num,num+cnt);ans1=dfs(0,0,1,1);memset(f,0xef,sizeof(f));cnt=0;while(a) num[cnt++]=a%10,a/=10;reverse(num,num+cnt);ans2=dfs(0,0,1,1);cout<<ans1-ans2;return 0;}
这太好了!当你学会这道例题的两种解法时,你就已经理解数位dp的80%了!
很明显,记忆化搜索更容易理解,也更暴力,也更模板化,基本能应对大部分题目了。
由于数位dp的题目过于模板+思维,所以请大家自行去折磨自己吧!
二、状态压缩dp
1.什么是状压dp
状态压缩dp,简称状压dp。
状压更多与十进制无关。我们以二进制为例:
对于二进制串:0010101001,我们发现第3/5/7/10位是1,其他位是0。
如果我们赋予这个1一个特殊含义,比如这个位置有个人。那么我们可以用一个二进制串表示某一排的人物排列状态。
设长度为m,由于每一位都是0或1,所以有种情况。
如果再用十进制数x表示二进制串,则x范围是:0~
。
这就是状压dp!用十进制数表示某一进制串,进而表示某一种排列状态。
2.如何实现状压dp
来道例题练练手!
在国际象棋中,国王能攻击到它上、下、左、右、左上、左下、右上、右下八个方向上附近的各一个格子,共 8 个格子。在 N×N 的棋盘里面放 K 个国王,使他们互不攻击,求共有多少种摆放方案。其中,1≤N≤9,0≤K≤N×N。
很明显,我们可以用十进制数表示二进制串,每一位上1表示有国王,0表示没有国王。
判断每个串内部合法,需要其满足没有相邻的1。
也就是说,(x&(x<<1))==0时是合法的,!=0时是不合法的。可以思考一下为什么。
同时,判断上下相邻的两个串合法,需要其满足没有重叠下标的1和相邻的1。
也就是说,(x&y)==0&&(x&(y<<1))==0&&(y&(x<<1))时是合法的,否则不合法。
代码如下:
ll n,k,f[10][(1<<9)+10][200],ans;vector hefa;ll calc(ll x){ll cnt=0;while(x) cnt++,x-=(x&(-x));return cnt;} //calc函数求当前的串中1的个数int main(){cin>>n>>k;f[0][0][0]=1;for(int i=0;i<(1<<n);i++) if(!(i&(i<<1))) hefa.push_back(i);for(ll i=1;i<=n;i++)for(ll x:hefa)for(ll y:hefa){if((x&y)||(x&(y<<1))||(y&(x<<1))) continue;ll calcy=calc(y);for(ll c=calcy;c<=k;c++) f[i][y][c]+=f[i-1][x][c-calcy];}for(ll i:hefa) ans+=f[n][i][k];cout<<ans;return 0;}
恭喜你,当你学会这一道题时,你已经学会状压dp的80%了!
三、总结
今天浅讲一下与进制有关的dp,说实话这真的很恶心。
但是没事,只要你们学会那80%就行啦!
goodbye!明天见!