七轴双臂机器人防碰撞检测（思路——含工程项目实现方式）_双臂机器人碰撞检测

七轴双臂机器人防碰撞检测（思路——含工程项目实现方式）

Readme

该碰撞检测方案仅适用于双臂机器人之间，而非避障、规划等碰撞检测方案。请谨慎食用。
机械臂拖动，机械臂逆运动的防碰撞检测方案都可以用此类方式。
食用之前请先下载论文：《双臂机器人自碰撞检测及其运动规划》——吴长征…等doi:10.16183/j.cnki.jsjtu.2018.01.008

设计流程图

（保密协议，没法放图出来，但是可以自己看看这个流程）
（开始>末端运动>根据末端位姿，利用运动学逆解求得各关节、连杆位姿>给各个连杆建立包围盒>将右臂各个连杆映射在左臂的基坐标系下>对各个连杆进行碰撞预测（判断不靠近继续拖动，靠近计算杆件之间最小距离）>计算相交杆件的最小距离>是否小于安全距离（判断））

#mermaid-svg-MlM3O75NZJLB5JvT {font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-MlM3O75NZJLB5JvT .error-icon{fill:#552222;}#mermaid-svg-MlM3O75NZJLB5JvT .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-MlM3O75NZJLB5JvT .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-MlM3O75NZJLB5JvT .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-MlM3O75NZJLB5JvT .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-MlM3O75NZJLB5JvT .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-MlM3O75NZJLB5JvT .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-MlM3O75NZJLB5JvT .marker{fill:#333333;stroke:#333333;}#mermaid-svg-MlM3O75NZJLB5JvT .marker.cross{stroke:#333333;}#mermaid-svg-MlM3O75NZJLB5JvT svg{font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-MlM3O75NZJLB5JvT .label{font-family:\"trebuchet ms\",verdana,arial,sans-serif;color:#333;}#mermaid-svg-MlM3O75NZJLB5JvT .cluster-label text{fill:#333;}#mermaid-svg-MlM3O75NZJLB5JvT .cluster-label span{color:#333;}#mermaid-svg-MlM3O75NZJLB5JvT .label text,#mermaid-svg-MlM3O75NZJLB5JvT span{fill:#333;color:#333;}#mermaid-svg-MlM3O75NZJLB5JvT .node rect,#mermaid-svg-MlM3O75NZJLB5JvT .node circle,#mermaid-svg-MlM3O75NZJLB5JvT .node ellipse,#mermaid-svg-MlM3O75NZJLB5JvT .node polygon,#mermaid-svg-MlM3O75NZJLB5JvT .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-MlM3O75NZJLB5JvT .node .label{text-align:center;}#mermaid-svg-MlM3O75NZJLB5JvT .node.clickable{cursor:pointer;}#mermaid-svg-MlM3O75NZJLB5JvT .arrowheadPath{fill:#333333;}#mermaid-svg-MlM3O75NZJLB5JvT .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-MlM3O75NZJLB5JvT .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-MlM3O75NZJLB5JvT .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-MlM3O75NZJLB5JvT .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-MlM3O75NZJLB5JvT .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-MlM3O75NZJLB5JvT .cluster text{fill:#333;}#mermaid-svg-MlM3O75NZJLB5JvT .cluster span{color:#333;}#mermaid-svg-MlM3O75NZJLB5JvT div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-MlM3O75NZJLB5JvT :root{--mermaid-font-family:\"trebuchet ms\",verdana,arial,sans-serif;}各关节连杆位姿否是否是开始末端运动映射是否相互靠近计算相交杆件的最小距离是否小于安全距离警报发出停止运动

包围盒基本原理

AABB包围盒的算法是基于边界平面建立的一个最小的长方体，该长方体可以框住整个需要被包围的物件，包括物件不同的姿态。
OBB包围盒算法则是基于该物体的平面生成的等距平面构成的立方体/圆柱体/球体。（这样表达在圆柱和球体里是不合适的，但类似）OBB是会根据物体姿态变化而变化，即旋转，平移。

AABB 简单高效 准确度较低 OBB 复杂难算 位姿明确，准确度高

Minkowski空间两点距离计算

闵可夫斯基距离（Minkowski Distance）是一种用于衡量多维空间中两点间距离的通用公式，它是曼哈顿距离和欧氏距离的推广形式。其数学公式如下：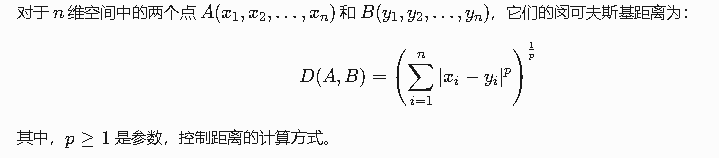

p在不同参数下会退化成不同的公式，适用性拉满。

空间中两线段距离计算

重中之重，前面我们引入了AABB OBB这种比较抽象的概念，实际上他们不适用在工控机。（算力不大够，整个项目不只有防碰撞，还有规划、等一堆的shit）所以连杆抽象化成圆柱后再抽象化成一根首尾相连的线段，自带方向。通过空间中两线段距离公式来计算。
OK，Now你得接受这个设定。他已经不是连杆了，而是很多的线段。
（可以在论文中找到对应的就种状态）
空间中两直线会呈现出9种状态。
用代码的思路来看，我们需要得到的输出是：两个连杆之间的最短距离。而这9种状态相当于列出了9个方程式，满足某些条件将会有怎样的表征。
那么我们的输入就是：两个连杆在空间中的状态；即连杆长度，连杆在空间中的位姿。
连杆长度可以通过空间两点之间距离得到，连杆位姿可以通过相对坐标系得到。
那么到这里，就可以看出输入的项，无论如何都是和坐标系有关联。预处理的思路就很好理解了。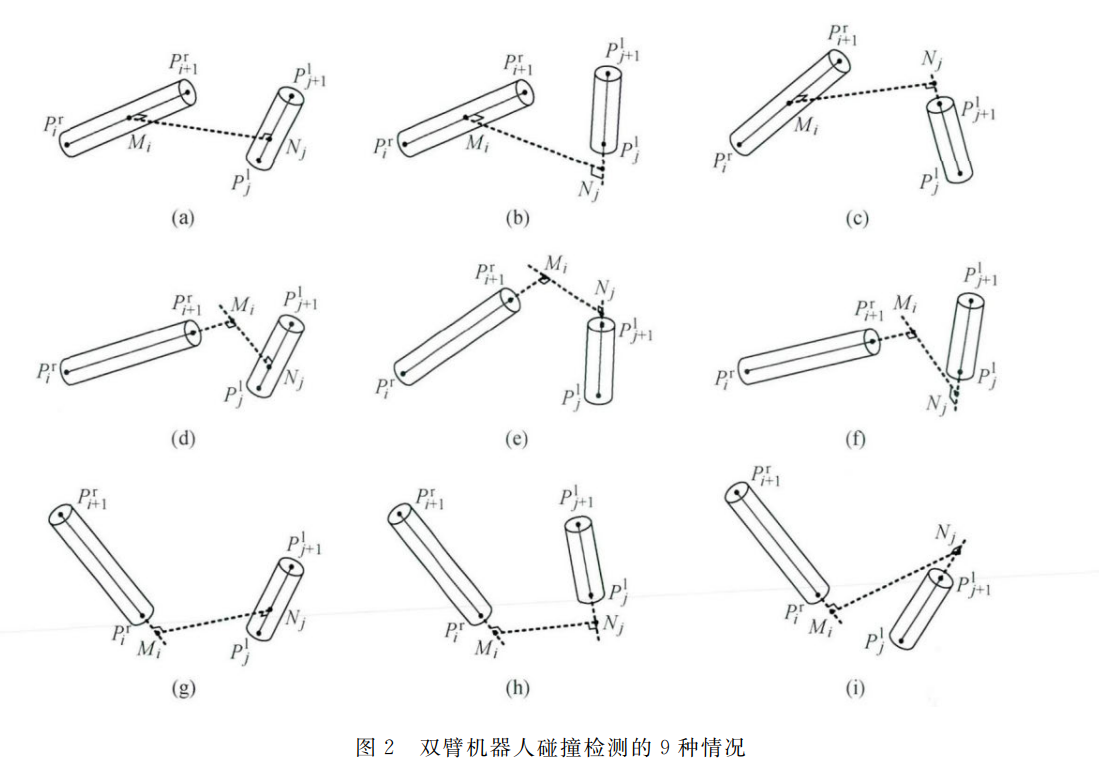

结合所有连杆都是线段的概念，取没跟两岸的关节点的连线，可以做出两条线段的公垂线段MN，其中，MN分别是右臂第i连杆/左臂第j连杆上的一点。其实就是找到两个线段的模拟交点（投影相交）在何处，他们相交如果在都在上端，即(e)，MN两个点都在上端，那么理论上他们i+1 和 j+1端更靠近。那么我们就取i+1和j+1的坐标点，并且用闵可夫斯基p=2的退化公式计算出距离。

诶聪明的你现在发现，实际在求这几个点的距离：

j-1 j+1 inside i-1 Pi-1 Pj-1 Pi-1 Pj+1 Pi-1 N i+1 Pi+1 Pj-1 Pi+1 Pj+1 Pi+1 N Inside M Pj-1 M Pj+1 M N

而要判断这个公垂点MN到底在哪，则需要通过公式计算。公式照常套进去就好了。不用解释

WTF？？ 这个k1 k2怎么求。(这里提供两个思路，实际上是一样的，但其中一个用矩阵来看)
闷了兄弟，这有四个参数要求，只有俩式子啊

方法1：

转个思路，MN两个点的距离公式我们不是已经知道了吗，得到第三条公式：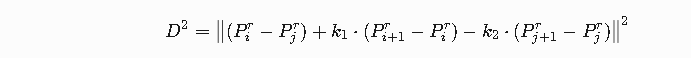

把MN转换成一个参数，不管他死活，能够计算出关于k1,k2的表达式。回忆一下我们在干啥，求最小值，极值！ 哦哦哦可以用 偏导求变化为0的点，就是极点，所以对D^2（单调递增函数啊兄弟） 求k1,k2的偏导。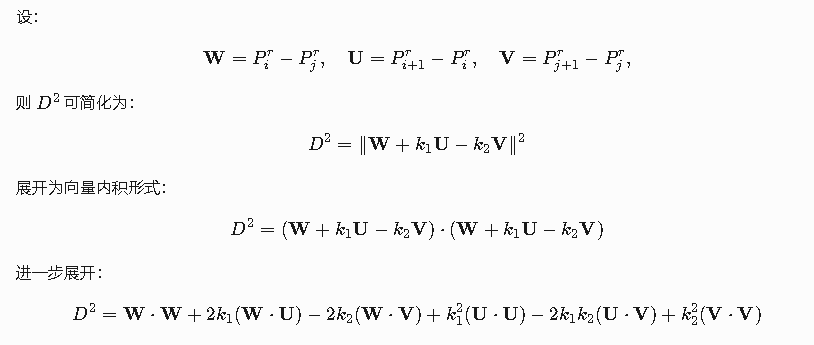

至此计算完成；

方法2：

直接来开干
直接就是把公式塞进去，很无脑，也不懂为什么要这么塞是吧？（这里有告诉你为啥，感兴趣可以跳到最后）Min(M-N)^2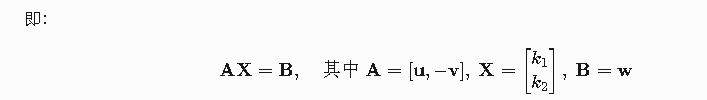

至此计算结束。

实机调试（Disgusting）

各关节实际位姿

七轴机械臂各关节的实际坐标你得回推啊！兄弟，默认D-H 构建出来的模型是12、34、56的坐标是同一个，7和工具器械盒是一个。所以要通过D-H模型计算出来的关节位姿以后平移回原来的位置。（此时姿态不会发生变化）正逆解这些东西，俺就不说了，比较基础。CSDN上好多相关的了。

最短距离不是最短距离？

上面两种计算两线段间最短距离的方法居然不是实际的距离？经过几天的摸索，发现有两个原因。

1. 实际上最短距离并不是求取的公垂线。
2. 明明看着6轴的距离要比5轴的近，但是计算出来的居然差不多？

首先第一个坑，线段是有限长的，但是计算中出现的>1 <0 这两种情况都是拓展到直线来看的。所以会形成一定的夹角，所以计算出来的线段长度需要减去这个由于夹角不同而造成的不同的膨胀距离。
第二个坑在于我们理想的认为56轴同一个杆上，他们的位姿一样，只是平移后位置不一。BUT！这是理想，计算出来的可能会有偏差，导致他俩相差的不多，比如6轴 =174.3245 和 5轴=174.6544 这样的数据，在工控机PLC里计算出来的就有差别，导致认为5轴更靠近，因而选取五轴的膨胀直径和夹角。

滤波！！！！！！（后面单独说吧）

在数学上我们不会觉得有啥问题，但是在计算机里头，开个根号，取个平方，除一个数都会在每一个时刻计算出不同的值。（机械臂只是我们肉眼看不到的抖动，电机位置肯定也会有误差。）这就导致出现的原始信号噪声很大，通过各种滤波器降噪以及设定状态机来解决会让整个项目更加有逻辑和准确。

啥是超静定方程