选择排序：简单但低效的排序策略

选择排序：简单但低效的排序策略

大家好！今天我们来聊聊排序算法中的一位\"老朋友\"——选择排序。想象一下你在整理一副扑克牌，每次从手中剩余的牌中找出最小的一张，放到已排序的那一叠的最上面，如此反复直到所有牌都排好序。这种\"每次找最小\"的思想正是选择排序的核心。

在实际编程中，我们经常会遇到需要排序的场景：从数据库查询结果排序到前端表格展示，排序无处不在。虽然现代编程语言都提供了高效的排序函数，但理解基础排序算法的工作原理对我们写出更好的代码大有裨益。

**为什么学习选择排序？**虽然效率不高，但选择排序的简单性使其成为学习排序算法的理想起点。理解它可以帮助我们掌握更复杂的算法。

一、选择排序的执行流程

理解了基本概念后，我们来看看选择排序的具体执行流程。选择排序就像是一场\"选秀比赛\"，每次从待选元素中选出最\"优秀\"（最小或最大）的一个，放到已排序区域的末尾。

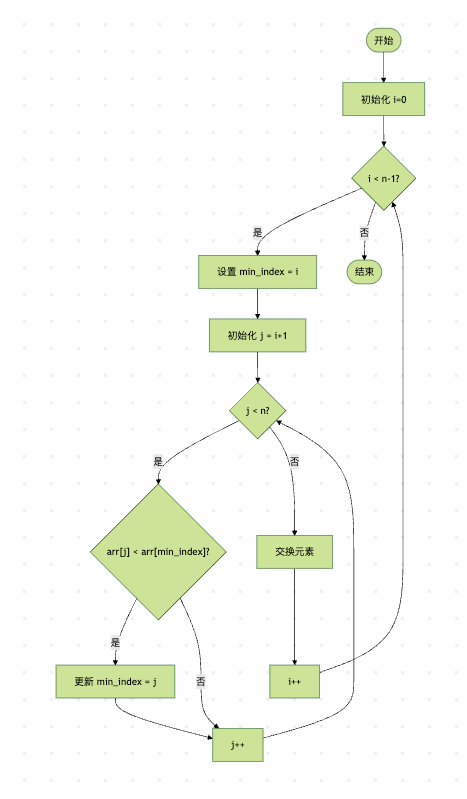
图1：选择排序流程图。外层循环控制排序轮次，内层循环寻找最小值，找到后与当前位置交换。

选择排序的具体步骤：

1. 从数组的第一个元素开始，假设它是最小值
2. 遍历剩余元素，寻找真正的最小值
3. 找到最小值后，与当前位置的元素交换
4. 移动到下一个位置，重复上述过程
5. 直到所有元素都排好序

二、选择排序的技术实现

理解了执行流程后，我们来看看如何用代码实现选择排序。我通常是这样做的：

public class SelectionSort { public static void sort(int[] arr) { int n = arr.length; // 外层循环控制排序轮次 for (int i = 0; i < n - 1; i++) { // 假设当前i位置是最小值 int minIndex = i; // 在剩余元素中寻找更小的值 for (int j = i + 1; j < n; j++) { if (arr[j] < arr[minIndex]) {  minIndex = j; } } // 如果找到更小的值，则交换 if (minIndex != i) { int temp = arr[i]; arr[i] = arr[minIndex]; arr[minIndex] = temp; } // 打印每一轮的结果（用于理解） System.out.println(\"第\" + (i + 1) + \"轮后: \" + Arrays.toString(arr)); } } public static void main(String[] args) { int[] arr = {64, 25, 12, 22, 11}; System.out.println(\"排序前: \" + Arrays.toString(arr)); sort(arr); System.out.println(\"排序后: \" + Arrays.toString(arr)); }}

代码1：基本选择排序的Java实现。包含外层循环控制轮次，内层循环寻找最小值，找到后进行交换。

**代码解析：**这段代码清晰地展示了选择排序的核心逻辑。外层循环的i表示当前要填充的位置，内层循环从i+1开始寻找最小值，找到后与i位置交换。

考虑到实际应用中可能需要降序排序或对复杂对象排序，我们可以对代码进行扩展：

public class GenericSelectionSort { // 支持泛型和自定义比较器的选择排序 public static <T> void sort(T[] arr, Comparator<? super T> comparator) { int n = arr.length; for (int i = 0; i < n - 1; i++) { int extremeIndex = i; for (int j = i + 1; j < n; j++) { if (comparator.compare(arr[j], arr[extremeIndex]) < 0) {  extremeIndex = j; } } if (extremeIndex != i) { T temp = arr[i]; arr[i] = arr[extremeIndex]; arr[extremeIndex] = temp; } } } public static void main(String[] args) { // 测试整数数组降序排序 Integer[] numbers = {3, 1, 4, 1, 5, 9}; sort(numbers, (a, b) -> b - a); System.out.println(\"降序排序: \" + Arrays.toString(numbers)); // 测试字符串数组按长度排序 String[] words = {\"apple\", \"pear\", \"banana\", \"kiwi\"}; sort(words, Comparator.comparingInt(String::length)); System.out.println(\"按长度排序: \" + Arrays.toString(words)); // 测试对象数组排序 Person[] people = { new Person(\"Alice\", 25), new Person(\"Bob\", 21), new Person(\"Charlie\", 30) }; sort(people, Comparator.comparingInt(Person::getAge)); System.out.println(\"按年龄排序: \" + Arrays.toString(people)); }}class Person { String name; int age; // 构造方法和getter省略...}

代码2：泛型选择排序实现。支持任意类型和自定义比较器，提高了代码的复用性。

**注意：**虽然我们实现了泛型版本，但在实际项目中，对于大规模数据排序，建议使用Java内置的Arrays.sort()或Collections.sort()，它们基于更高效的算法实现。

三、选择排序的性能分析

了解了实现方式后，我们来看看选择排序的性能特点。选择排序就像一个不知疲倦的质检员，无论产品已经多么整齐，他还是要一个个检查。

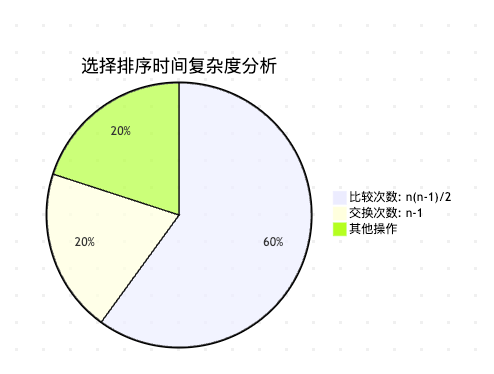
图3：选择排序操作分布。比较操作占主要部分，交换次数相对较少。

情况 时间复杂度 说明 最好情况 O(n²) 即使数组已经有序，仍需完整比较 平均情况 O(n²) 典型情况下需要n(n-1)/2次比较 最坏情况 O(n²) 与平均情况相同 空间复杂度 O(1) 原地排序，不需要额外空间

表1：选择排序时间复杂度分析。无论输入如何，时间复杂度都是O(n²)。

**性能特点：**选择排序的主要优点是交换次数少（最多n-1次），对于交换成本高的场景（如移动大对象）可能有优势。但它的时间复杂度决定了它不适合大规模数据。

四、选择排序的优缺点

理解了性能特点后，我们来看看选择排序的优缺点。就像每件工具都有其适用场景一样，选择排序也有它的用武之地。

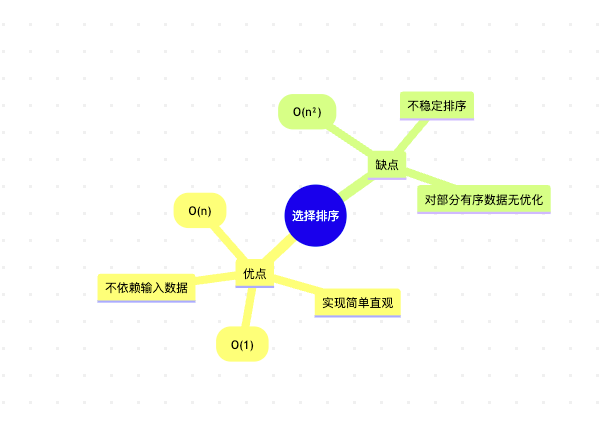
图5：选择排序优缺点思维导图。它简单直观但效率不高，适合小规模数据或对交换次数敏感的场景。

优点详细说明：

• **实现简单：**算法逻辑直白，容易理解和实现，适合教学目的
• **空间效率高：**只需要常数级别的额外空间，内存占用小
• **交换次数少：**最多n-1次交换，对于交换成本高的场景有优势
• **不依赖输入数据：**无论输入如何，比较次数相同，性能可预测

缺点详细说明：

• **时间复杂度高：**O(n²)的时间复杂度使其不适合大规模数据
• **不稳定：**选择排序是不稳定的排序算法（相同元素的相对位置可能改变）
• **对部分有序数据无优化：**即使输入已经部分有序，仍需完整比较

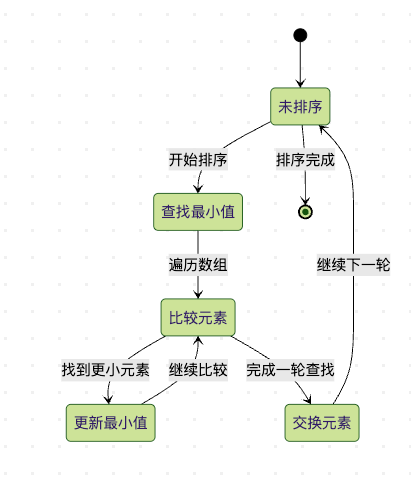
图6：选择排序状态图。展示了算法在不同状态间的转换过程。

五、选择排序的优化方向

虽然选择排序效率不高，但我们还是可以探讨一些可能的优化方向。就像给老式汽车加装现代设备一样，我们可以尝试改进这个基础算法。

1. 双向选择排序（鸡尾酒选择排序）

类似于冒泡排序的鸡尾酒排序，我们可以在每轮中同时寻找最小和最大值：

public class BidirectionalSelectionSort { public static void sort(int[] arr) { int left = 0, right = arr.length - 1; while (left < right) { int minIndex = left, maxIndex = right; // 找出当前范围内的最小和最大值 for (int i = left; i <= right; i++) { if (arr[i] < arr[minIndex]) minIndex = i; if (arr[i] > arr[maxIndex]) maxIndex = i; } // 将最小值交换到left位置 swap(arr, left, minIndex); // 如果最大值原本在left位置，由于已经交换，需要更新maxIndex if (maxIndex == left) maxIndex = minIndex; // 将最大值交换到right位置 swap(arr, right, maxIndex); left++; right--; } } private static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; }}

代码3：双向选择排序实现。每轮同时找到最小和最大值，理论上可以减少大约一半的循环次数。

2. 使用堆结构优化

选择排序的核心操作是\"选择最小元素\"，这正是堆数据结构的强项。基于这个思路，我们可以得到堆排序算法：

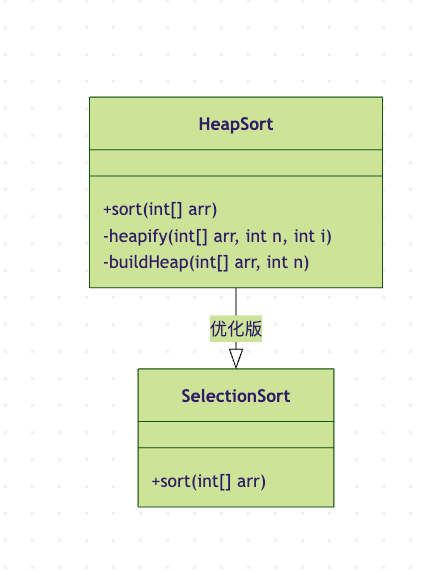
图7：堆排序与选择排序的关系。堆排序可以看作是对选择排序中\"选择\"过程的优化。

**实际应用建议：**在真实项目中，如果数据量小（如n<50），选择排序可能比其他算法更快（因为常数因子小）。但对于大规模数据，建议使用更高效的算法如快速排序、归并排序或堆排序。

六、总结

通过今天的讨论，相信大家对选择排序有了更深入的理解。让我们总结一下本文的主要内容：

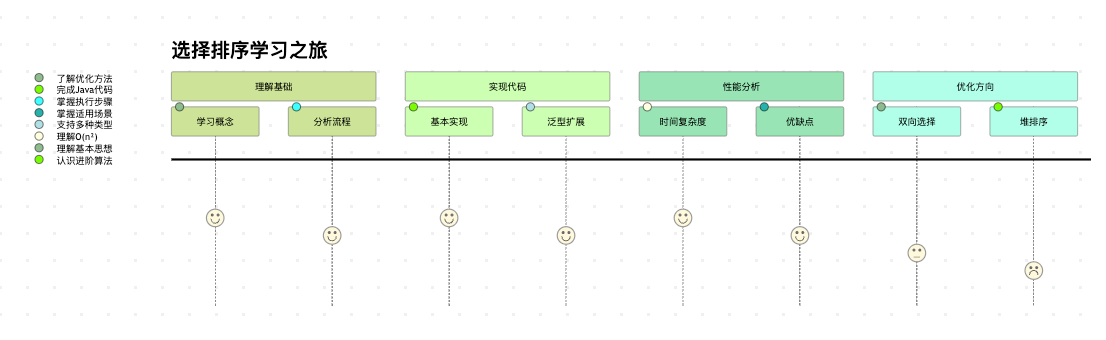
图8：选择排序学习路线图。展示了从基础概念到优化方向的学习过程。

1. **基本概念：**选择排序是一种简单直观的排序算法，通过不断选择剩余元素中的最小值来排序
2. **执行流程：**外层循环控制轮次，内层循环寻找最小值，找到后交换到正确位置
3. **时间复杂度：**无论最好、最坏还是平均情况，时间复杂度都是O(n²)
4. **空间复杂度：**O(1)，是原地排序算法
5. **优缺点：**实现简单、交换次数少，但效率不高且不稳定
6. **优化方向：**双向选择、利用堆结构等

**最终建议：**虽然选择排序在实际应用中很少直接使用，但理解它的工作原理对我们学习更复杂的算法很有帮助。它是理解排序算法的重要基础，建议初学者认真掌握。

希望大家通过这篇文章对选择排序有了全面的认识。在实际工作中，我们可以根据具体场景选择合适的排序算法。记住，没有最好的算法，只有最适合的算法。