matlab:分形光子晶体传输矩阵法复现_光子晶体 矩阵法

复现Self-Similarity Properties of Complex Quasi-Periodic Fibonacciand Cantor Photonic Crystals这篇论文的图3，其他图是类似的，不再重复。

这篇论文研究了准周期（QP）光子晶体（PhC）的结构修改对其光谱响应自相似性的影响，重点分析了Fibonacci和Cantor两种典型结构。使用传输矩阵方法（TMM）计算一维光子晶体的透射光谱，验证了结构修改对自相似性的影响。高阶（如Fib8, Fib14, Fib20）光谱的自相似性。另外一种Cantor结构：基于分形迭代规则生成的自相似结构，通过递归替换中间部分为L材料（如将H层三等分后替换中间段），其光谱同样具有自相似性。

% 主函数参数设置

n_H = 2.3;          % TiO2折射率

n_L = 1.45;         % SiO2折射率

c = 3e8;            % 光速(m/s)

v0 = 600e12;        % 中心频率(Hz)

lambda0 = c / v0;   % 中心波长(m)

d_H = lambda0/(4*n_H);  % H层厚度(m)

d_L = lambda0/(4*n_L);  % L层厚度(m)

% 生成8阶Fibonacci序列

n_order = 8;

sequence = generate_fibonacci(n_order);

% 转换为层结构

n_layers = [];

d_layers = [];

for i = 1:length(sequence)

    if sequence(i) == \'H\'

        n_layers = [n_layers n_H];

        d_layers = [d_layers d_H];

    else

        n_layers = [n_layers n_L];

        d_layers = [d_layers d_L];

    end

end

% 频率设置

num_points = 1000;

v_normalized = linspace(0.5, 1.5, num_points);

v = v_normalized * v0;

% 预分配透射率数组

T = zeros(1, num_points);

% 计算各频率响应

for f_idx = 1:num_points

    lambda = c / v(f_idx);  % 当前波长

    % 初始化传输矩阵

    M_total = eye(2);

    n_prev = 1;  % 入射介质为空气

    % 计算各层矩阵

    for layer_idx = 1:length(n_layers)

        n_curr = n_layers(layer_idx);

        d_curr = d_layers(layer_idx);

        % 界面矩阵

        r = (n_prev - n_curr)/(n_prev + n_curr);

        t = 2*n_prev/(n_prev + n_curr);

        M_interface = [1 r; r 1]/t;

        % 传播矩阵

        delta = 2*pi*n_curr*d_curr/lambda;

        M_prop = [exp(-1i*delta) 0; 0 exp(1i*delta)];

        % 更新总矩阵

        M_total = M_total * M_interface * M_prop;

        n_prev = n_curr;

    end

    % 出射界面到空气

    r_out = (n_prev - 1)/(n_prev + 1);

    t_out = 2*n_prev/(n_prev + 1);

    M_out = [1 r_out; r_out 1]/t_out;

    M_total = M_total * M_out;

    % 计算透射率

    T(f_idx) = 1/abs(M_total(1,1))^2;

end

% 绘制结果

figure;

plot(v_normalized, T);

xlabel(\'归一化频率 (v/v_0)\');

ylabel(\'透射率\');

title([\'Fibonacci第\', num2str(n_order), \'阶透射谱\']);

axis([0.5 1.5 0 1]);

grid on;

% Fibonacci序列函数

function seq = generate_fibonacci(n)

    if n == 1

        seq = \'L\';

    elseif n == 2

        seq = \'H\';

    else

        s_prev_prev = \'L\';

        s_prev = \'H\';

        for i = 3:n

            s_curr = [s_prev s_prev_prev];

            s_prev_prev = s_prev;

            s_prev = s_curr;

        end

        seq = s_prev;

    end

end

运行后结果如下和论文中一致

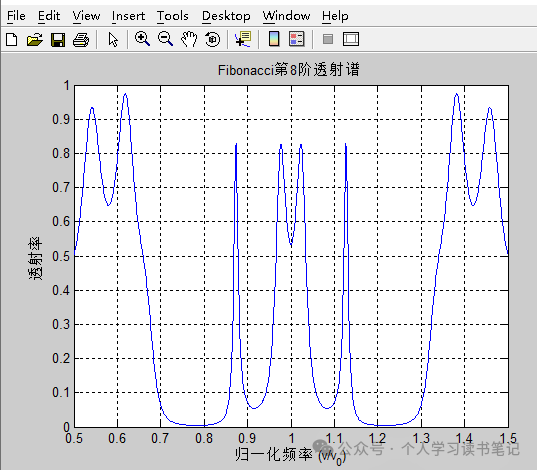
该研究为准周期光子晶体的设计提供了理论依据，证明通过结构修改可调控光谱特性（如带隙位置、滤波性能），同时保留自相似性这一关键特征。这对光学滤波器、传感器和激光谐振腔等器件的优化具有实际应用价值。