动态规划----股票买卖问题(详解)_买卖股票问题
目录
一.买卖股票的最佳时机:
二.买卖股票的最佳时机含冷冻期:
三.买卖股票的最佳时期含⼿续费:
四.买卖股票的最佳时机III:
五.买卖股票的最佳时机IV:
买卖股票的最佳时机问题介绍:动态规划买卖股票的最佳时机是一个经典的算法问题。该问题的目标是在给定的股票价格数组中,找到最大的利润,即最佳的买入和卖出时间,使得买入时间早于卖出时间。
下面我们通过一些例题,来解决这一类动态规划的问题:
一.买卖股票的最佳时机:
- 题目链接:121. 买卖股票的最佳时机 - 力扣(LeetCode)
- 题目描述:
给定一个数组
prices,它的第i个元素prices[i]表示一支给定股票第i天的价格。你只能选择某一天买入这只股票,并选择在未来的某一个不同的日子卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回
0。

①.动态规划解法:
- 一.状态表示dp[ i ][ j ]:下标为
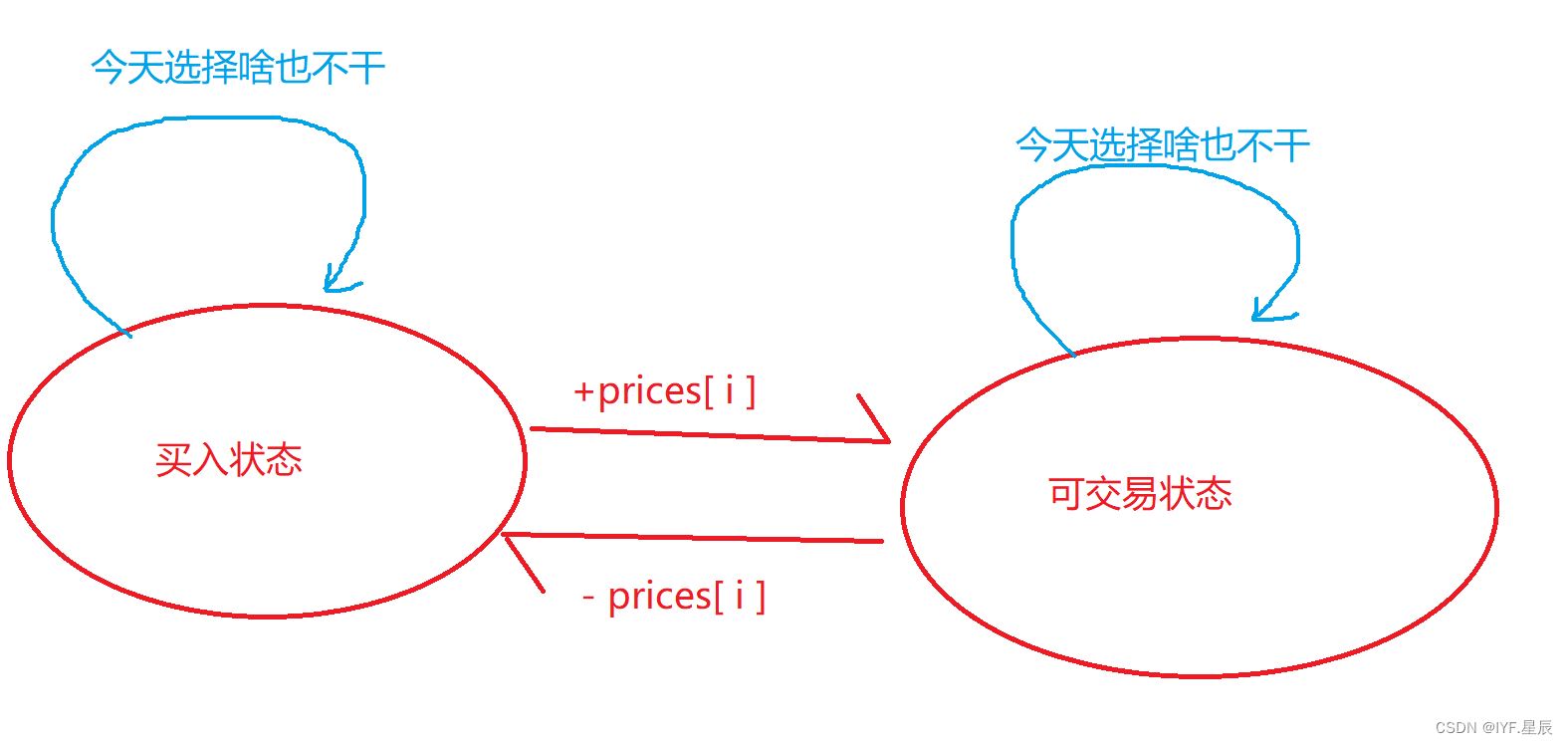
i这一天结束的时候,手上持股状态为j时,我们持有的最大利润。这里我们定义状态 j (两种情况)分别为:- 0买入状态
- 1可交易状态
- 二.状态转移方程:
- dp[ i ][ 0 ] = Math.max( dp[ i - 1 ][ 0 ], -prices[ i ]) ; ①.在前面一天已经是买入状态,今天选择什么也不干,今天结束后,是买入状态。②.前面是可交易状态,今天选择买入,则今天结束后是买入状态,这里注意不是dp[ i - 1][ 1 ] - prices[ i ];因为只能交易一次,如果今天选择买入,那后面一定要卖出(这算一次交易),此时才可能有最大利润。则前面不能有交易,利润为0.
- dp[ i ][ 1 ] = Math.max( dp[ i - 1][ 1 ],dp[ i - 1][ 0 ] + prices[ i ]);①.前面一天是可交易状态,今天选择什么也不干,今天结束后是可交易状态。②.前面一天是买入状态,今天选择卖出,今天结束后是可交易状态。
- 三.初始化:根据状态表示:
- dp[ 0 ][ 0 ] = - prices[ 0 ];第一天选择买入,此时利润为 - prices[ 0 ]
- dp[ 0 ][ 1 ] = 0;第一天选择什么也不干或则交易一次,此时的利润为0;
- 四.填表顺序:根据状态转移方程,从左往右,从上往下填写.
- 五.返回值:dp[ n - 1 ][ 1 ];n为prices数组的长度,最后一天结束后,是可交易状态,此时为最大利润.
各个状态关系图:
代码详解:
class Solution { // 1. 创建 dp 表 // 2. 初始化 // 3. 填表 // 4. 返回值 public int maxProfit(int[] prices) { int n = prices.length; int[][] dp = new int[n][2]; //初始化 dp[0][0] = -prices[0]; dp[0][1] = 0; for(int i = 1;i < n;i++){ //注意这里不是dp[i - 1][1] - prices[i]; dp[i][0] = Math.max(dp[i - 1][0], - prices[i]); dp[i][1] = Math.max(dp[i - 1][1],dp[i - 1][0] + prices[i]); } //返回值 return dp[n - 1][1]; }}
②.暴力解法(相对简单这里给出解题过程):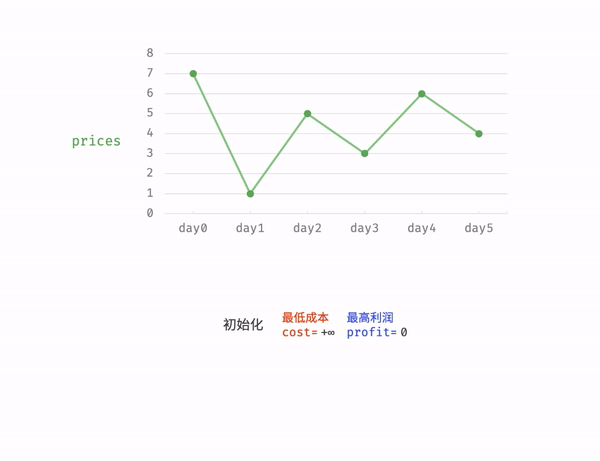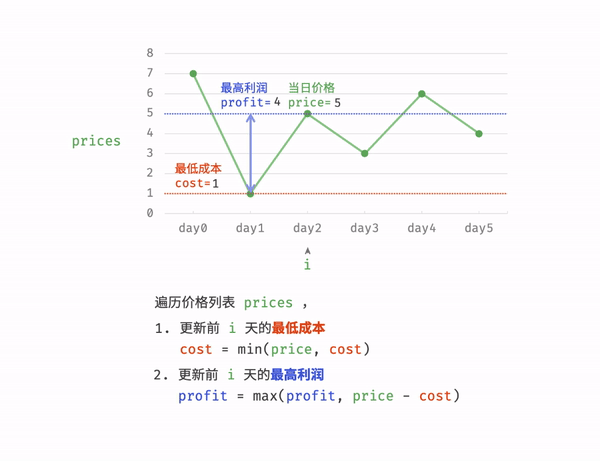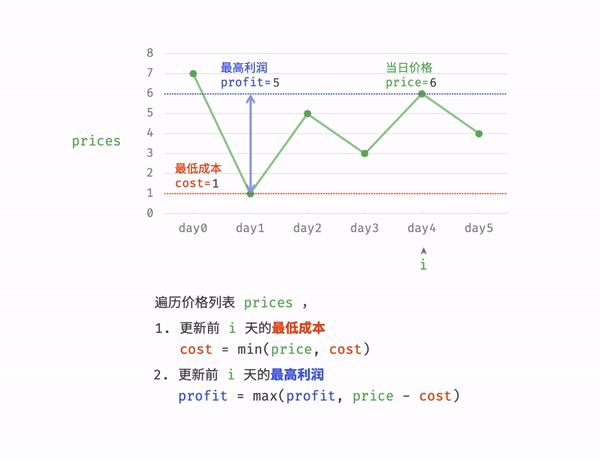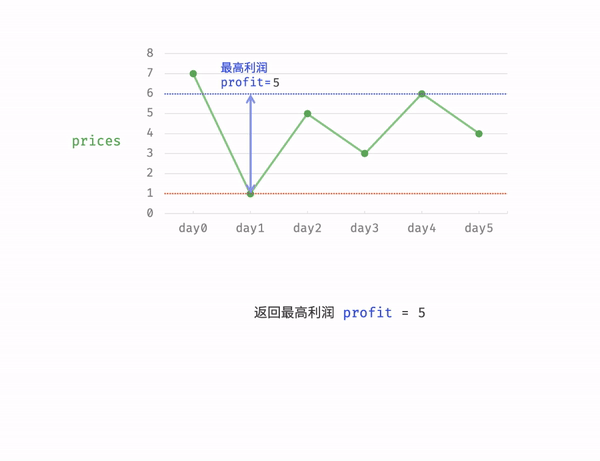
代码详解:
class Solution { public int maxProfit(int[] prices) { int cost = Integer.MAX_VALUE; int profit = 0; for(int price : prices){ cost = Math.min(cost,price); profit = Math.max(profit,price - cost); } return profit; }}运行结果: