数学建模学习——MATLAB模型
一. 灰色预测模型
-
cumsum(X0)
- 功能:计算向量
X0的累加和。 - 示例:
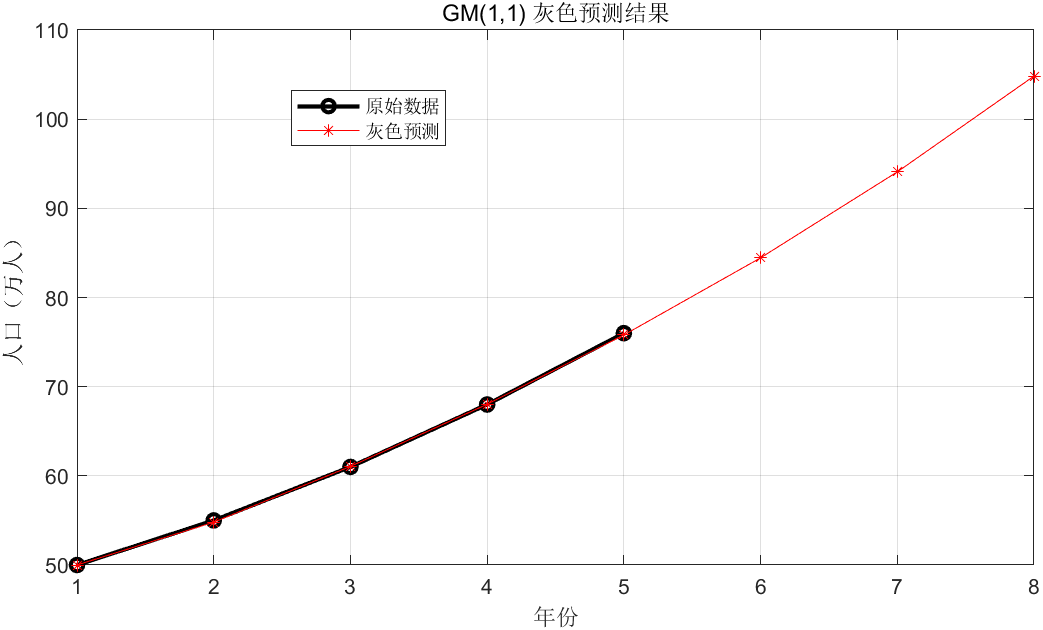
X0 = [50, 55, 61, 68, 76],则X1 = cumsum(X0) = [50, 105, 166, 234, 310]。
- 功能:计算向量
-
最小二乘求解模型参数
-
B\\Y:MATLAB 中求解线性方程组B·u = Y的最小二乘解(本质是拟合X0(k) = a·z₁(k) + b,其中z₁(k)是背景值)。u:参数向量[a, b],a是发展系数,b是灰作用量。a反映序列的增长 / 衰减趋势,|a|越小,预测精度通常越高;b反映外部驱动因素的影响。
-
预测模型(累加序列还原)
二. 逻辑回归模型
fitglm函数:拟合广义线性模型(Generalized Linear Model, GLM)。- 参数:
X:特征矩阵;Y:二元标签(0/1);\'Distribution\', \'binomial\':指定响应变量服从二项分布(适用于分类问题);\'Link\', \'logit\':指定连接函数为逻辑函数(Logit),将线性预测转换为概率。
- 返回值
mdl:训练好的逻辑回归模型对象,包含系数、拟合统计量等。 -
参数 Estimate(估计值) SE(标准误) tStat(t 统计量) pValue(p 值) (Intercept) -11.266 12.174 -0.925 0.35474 x1(使用时长) -1.073 1.932 -0.555 0.57868 x2(月消费) 0.32189 0.458 0.702 0.48242
- 参数:
-
卡方统计量(常量模型): 6.13,p 值 = 0.0467:- 对比 “仅含截距的空模型” 和 “当前含 x1、x2 的模型”:
- p 值 = 0.0467 < 0.05,说明 “加入 x1 和 x2 后,模型整体预测能力显著优于纯随机猜测”(尽管单个特征不显著,但整体有提升)。
三. 决策树模型
拟合决策树模型
tree = fitctree(X, Y, \'PredictorNames\', {\'出勤率\', \'作业得分\'}, ... \'ResponseName\', \'是否挂科\');fitctree函数:训练分类决策树模型。- 参数:
X:特征矩阵;Y:标签向量;\'PredictorNames\':自定义特征名称(提高可读性);\'ResponseName\':自定义标签名称。
- 返回值
tree:训练好的决策树对象,包含节点划分规则。
- 参数:
3. 可视化决策树
作业得分 < 65?
/ \\
是 否
挂科 出勤率 < 0.85?
/ \\
是 否
不挂科 挂科
四. 支持向量机模型
fitcsvm函数:训练二分类 SVM 模型。- 参数:
X:特征矩阵;Y:标签向量;\'KernelFunction\', \'linear\':使用线性核函数(生成直线分类边界);\'Standardize\', true:自动标准化特征(消除量纲影响,如评分和收入的单位差异);\'ClassNames\', [0 1]:指定标签类别名称。
- 返回值
svmModel:训练好的 SVM 模型,包含分类边界参数和支持向量。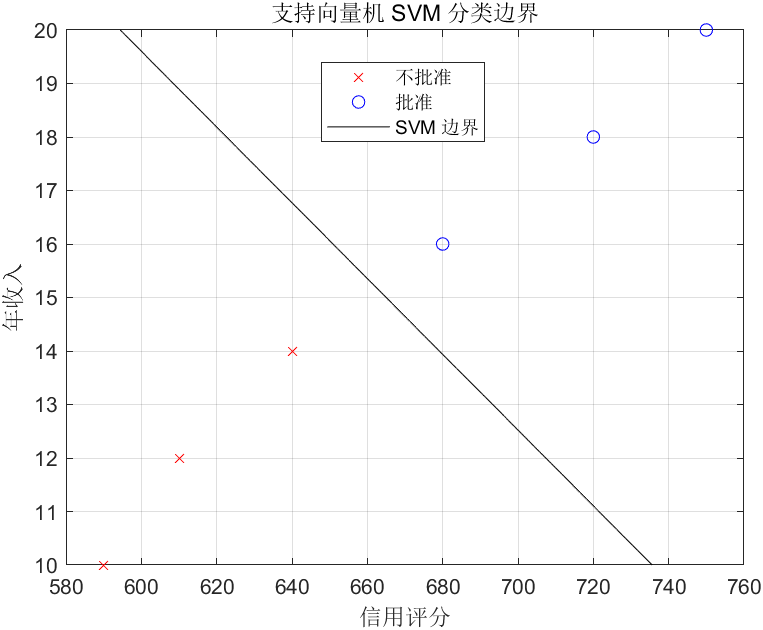
- 参数:
五. 人工神经网络模型
2. 创建神经网络
net = fitnet(10);fitnet函数:创建用于回归或函数逼近的前馈神经网络。- 参数:
10表示隐藏层有 10 个神经元。 - 网络结构:
- 输入层:3 个神经元(对应 3 个特征);
- 隐藏层:10 个神经元(默认使用 Tanh 激活函数);
- 输出层:1 个神经元(预测总成绩,线性激活)。
隐藏层的 10 个神经元不是固定的,它是一个需要人为设定的 “超参数”。这个数量的核心作用是控制神经网络对数据的拟合能力,直接影响模型的学习效果和泛化能力。
神经网络的核心是通过 “神经元” 模拟人脑的 “神经元连接”—— 每个神经元接收输入、通过激活函数处理后传递给下一层。隐藏层神经元数量没有固定规则,因为不同问题的复杂度不同:
- 如果数据很简单(比如线性关系明显),可能只需要 2-5 个神经元;
- 如果数据复杂(比如非线性关系强、特征多),可能需要 10-100 个甚至更多。
-
你给出的代码中用 10 个神经元,是针对 “学生成绩预测” 这个简单问题的合理尝试,换成 5 个或 15 个也能运行,只是效果可能不同。
神经元数量的具体作用
-
决定模型 “学习能力” 的强弱
- 神经元越多:模型能捕捉更复杂的关系(比如 “出勤率” 和 “期中成绩” 的交互影响),但容易 “过度学习”(把训练数据中的噪音当成规律)。
- 神经元越少:模型学习能力弱,可能连数据中的基本规律都抓不住(“欠拟合”)。
举例:如果用 100 个神经元拟合 6 个学生的数据(你的代码中只有 6 个样本),模型可能会精准 “记住” 每个学生的成绩,但遇到新学生时预测会很离谱(过度拟合)。
-
影响计算效率
- 神经元越多:计算量越大(训练时间变长),但对复杂数据更友好。
- 神经元越少:计算快,但可能无法处理复杂关系。
- 设置训练 / 测试划分
-
net.divideParam.trainRatio = 0.8; % 80% 训练net.divideParam.valRatio = 0.1; % 10% 验证net.divideParam.testRatio = 0.1; % 10% 测试 -
数据划分规则:
- 训练集:用于调整网络权重和偏置;
- 验证集:用于在训练过程中监测模型泛化能力,防止过拟合;
- 测试集:用于最终评估模型性能。
- 参数:
- 训练因 “梯度小于阈值” 而停止(不是因为达到最大迭代次数),说明模型参数已经收敛到稳定状态。
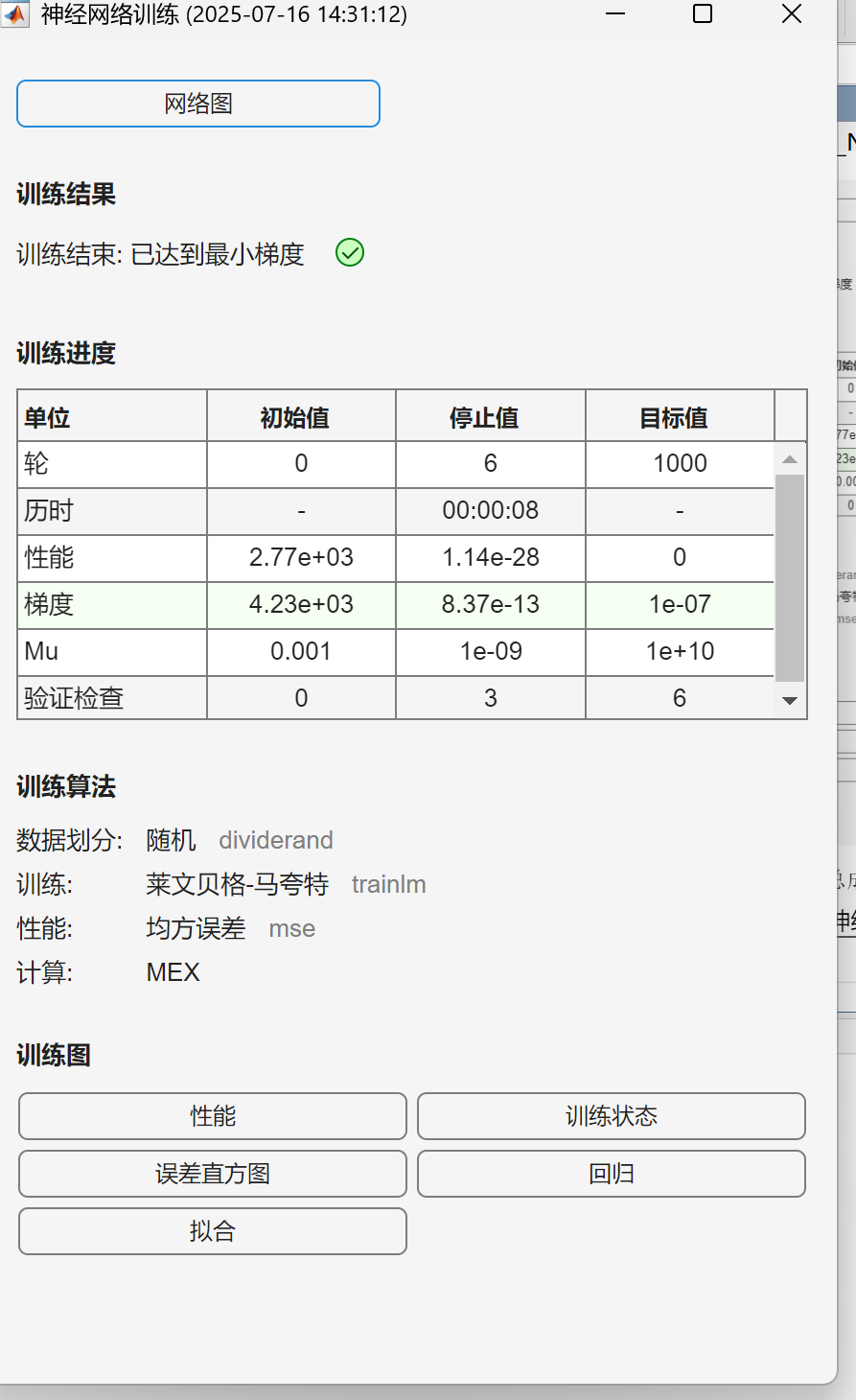
如何验证模型可靠性?
- 查看测试集性能:在训练报告的 “回归图” 或 “性能图” 中,检查测试集的 MSE 是否也接近 0。
-
单位 初始值 停止值 目标值 解读 轮(Epoch) 0 6 1000 仅迭代了 6 轮就收敛(远小于目标 1000 轮),说明数据简单或模型学习能力强。 历时 - 00:00:08 - 训练耗时 8 秒,非常快(因样本量小、模型简单)。 性能(MSE) 2.77e+03 1.14e-28 0 均方误差(Mean Squared Error),从初始的 2770 降到几乎 0,说明预测误差极小。 梯度 4.23e+03 8.37e-13 1e-07 梯度从 4230 降到远小于目标阈值(1e-7),参数更新已稳定。 Mu 0.001 1e-09 1e+10 Levenberg-Marquardt 算法的阻尼系数,越小表示越接近高斯牛顿法,收敛稳定。 验证检查 0 3 6 验证集误差连续 3 次未下降(触发早停机制前的检查)。
六. 层次分析法模型
准则层(目标层下的 “成本、交通、环境”3 个维度)的判断矩阵,用于表示 3 个准则之间的相对重要性。
- 行 / 列对应:成本(第 1 行)、交通(第 2 行)、环境(第 3 行)。
- 元素
C(i,j):表示第i个准则相对于第j个准则的重要性程度(采用 1-9 标度法)。- 例如:
C(1,2)=3表示 “成本” 比 “交通”重要 3 倍;C(3,1)=2表示 “环境” 比 “成本”重要 2 倍1. 准则层权重(如
W_criteria)表示准则层各因素(成本、交通、环境)的相对重要性。
- 示例:若
W_criteria = [0.5, 0.3, 0.2],表示:- 成本的重要性占比为 50%;
- 交通的重要性占比为 30%;
- 环境的重要性占比为 20%。
- 2. 方案层权重(如
W1、W2、W3) -
表示在某个准则下,各方案(城市 A、B、C)的相对优劣。
- 示例:若
W1 = [0.6, 0.3, 0.1](成本准则下的权重),表示:- 城市 A 的成本优势占比为 60%;
- 城市 B 的成本优势占比为 30%;
- 城市 C 的成本优势占比为 10%。
-
. 一致性检验的本质
验证专家的判断是否具有传递性(如 “若 A 比 B 重要,B 比 C 重要,则 A 比 C 重要”)。若不满足传递性,特征向量计算出的权重将失去意义。
- 例如:
- 综合得分计算逻辑:
矩阵乘法:方案层权重([W1, W2, W3],3×3 矩阵)与准则层权重(W_criteria,3×1 向量)相乘,得到每个城市的综合得分。综合得分A=W1A⋅W成本+W2A⋅W交通+W3A⋅W环境
其中: W1_A:城市 A 在 “成本” 准则下的权重(W1的第 1 行);W_{\\text{成本}}:“成本” 准则的权重(W_criteria的第 1 个元素);- 同理,累加交通、环境准则的加权贡献。
七. 熵权法模型
用途:
-
用于多指标综合评价;
-
在指标没有明显优劣排序、但需要综合排序的时候很有用(如评估城市发展水平、公司绩效、交通效率等);
-
常配合 TOPSIS、灰色关联度、AHP 等一起使用。
熵值 E
P(P == 0) = 1; % 防止 log(0) 报错E = -sum(P .* log(P)) / log(m); % 计算每个指标的熵值- 计算逻辑:
熵值反映指标的离散程度(信息量):
E(j)=−log(m)1∑i=1mP(i,j)⋅log(P(i,j))- 若某指标下所有城市的值相同(P(i,j)=1/m),则熵值最大(E(j)=1),说明该指标 “区分度低”;
- 若某指标下只有一个城市的值非零(P(i,j)=1,其他为 0),则熵值最小(E(j)=0),说明该指标 “区分度高”。
- 作用:
衡量指标的信息量(区分度):熵值越小,指标对决策的贡献越大。
6. 差异系数 d
d = 1 - E; % 差异系数 = 1 - 熵值- 计算逻辑:
差异系数与熵值负相关:- 熵值越小(指标区分度高),差异系数越大;
- 熵值越大(指标区分度低),差异系数越小。
- 作用:
将 “熵值” 转换为 “指标重要性” 的正向指标(差异系数越大,指标越重要)。
7. 熵权 w
w = d / sum(d); % 权重 = 差异系数 / 总差异系数- 计算逻辑:
对差异系数归一化,得到每个指标的权重:
w(j)=∑j=1nd(j)d(j)
(n 是指标数量,此处 n=4) - 作用:
表示每个指标在综合评价中的重要性占比(区分度高的指标权重更大)。
8. 综合得分 score
score = X_norm * w\'; % 加权求和:标准化数据 × 权重向量- 计算逻辑:
对每个城市,将其标准化后的指标值按熵权加权求和:
score(i)=∑j=1nXnorm(i,j)⋅w(j) - 作用:
综合所有指标的重要性,得到每个城市的综合评价得分。
八. TOPSIS模型
TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)的核心是:
- 找 “理想标杆”:构造 “正理想解”(所有指标最优)和 “负理想解”(所有指标最劣);
- 算 “距离”:每个方案与正 / 负理想解的距离;
在这个 TOPSIS 算法(优劣解距离法)的代码中,isBenefit 的 0 和 1 是根据指标的 “优劣判断逻辑” 来规定的,核心原则是:
- 1(正向指标):指标数值 越大越好(数值越大,代表方案越优);
- 0(负向指标):指标数值 越小越好(数值越小,代表方案越优)。
4. 归一化数据 X_norm
熵权法本身没有 “自动识别指标方向” 的能力,如果不对负向指标做额外处理,直接用原始数据计算,负向指标的 “高数值” 会被误当成 “优势”(因为熵权法的核心是 “数值波动大的指标权重高,且数值大的样本在该指标下得分高”),这会导致结果完全偏离实际业务逻辑。


