【CF】Day114——杂题 (贪心 + 图论 | LCM + 贪心 | 最大最小子序列 + 图论)

D. Paint the Tree

题目：

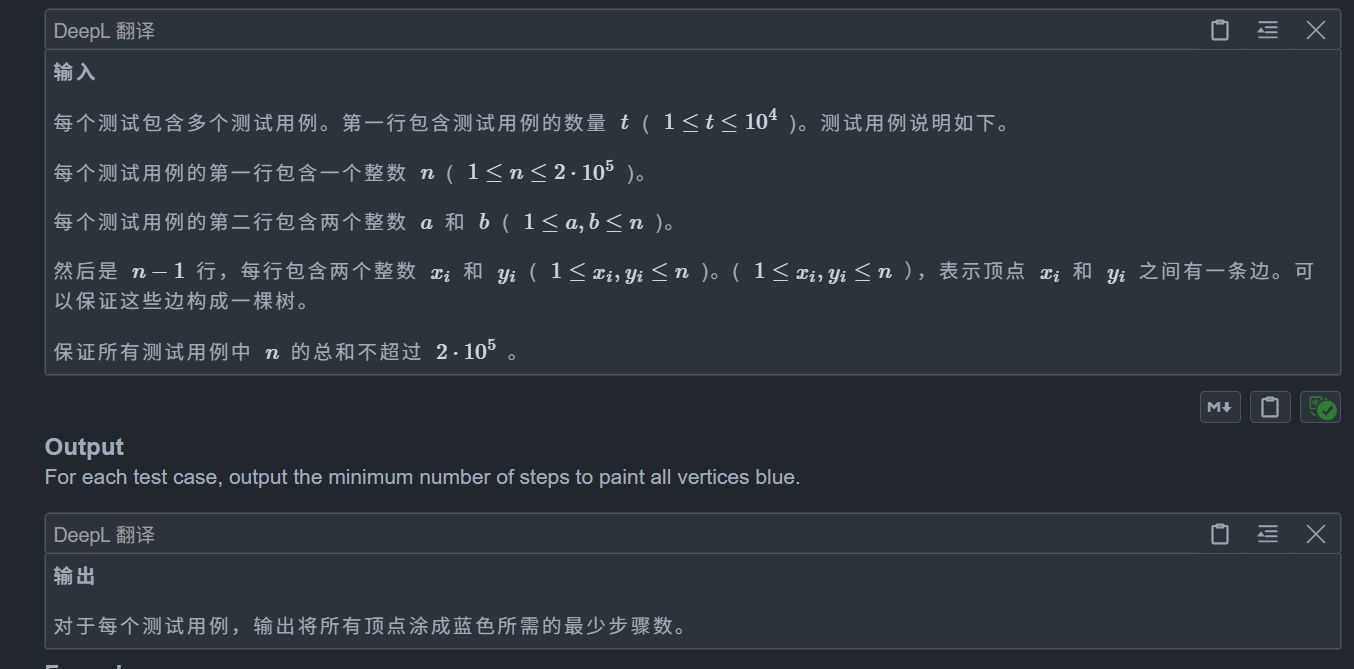思路：

贪心 + 图论

首先我们将题目缩减一下，如果只有 a 点我们怎么写？

显然我们的答案是 2 * (n-1) - mxdep，其中 mxdep 是节点最深的深度，为什么呢？因为既然我们要走完整个图，那么每一条路径都得走两边，而我们最后不需要回到出发点，所以我们最后走最长的路径即可，这样就不用走最长的两遍了

那么现在有一个点 b 怎么办？

我们贪心的想，我们肯定是让二者尽早回合最好，因为我们要让 b 走的无用功越短越好，所以我们让二者相向而行，二者回合的点就是一个新的根，然后以新的根做上诉操作即可

那如果二者的最短路径是奇数，无法相遇怎么办？

此时我们可以让 b 多走一步，这样还是一样的操作，因为由于不能回合，但是我们其实只要 b 能走到红色部分即可，所以我们可以想让 a 以最优方式行走，b 跟着 a 既可，这样虽然会相差一格，但是是无影响的

代码：

#include using namespace std;#define int long long#define yes cout << \"Yes\\n\"#define no cout <> n >> a >> b; vector<vector> g(n + 1); for (int i = 0; i > u >> v; g[u].push_back(v); g[v].push_back(u); } dep[a] = 0; auto dfsa = [&](auto &&self, int fa, int se) -> void { for (auto &son : g[se]) { if (son == fa) continue; dep[son] = dep[se] + 1; f[son] = se; self(self, se, son); } }; dfsa(dfsa, a, a); int root = b; int cnt = 0; while (dep[root] != (dep[b] + 1) / 2) { root = f[root]; cnt++; } if (dep[b] & 1) { root = f[root]; cnt++; } dep[root] = 0; dfsa(dfsa, root, root); int mxlen = 0; for (int i = 1; i <= n; i++) { mxlen = max(mxlen, dep[i]); } cout << cnt + (n-1)*2 - mxlen <> t; while (t--) { solve(); } return 0;}

C. Nikita and LCM

题目：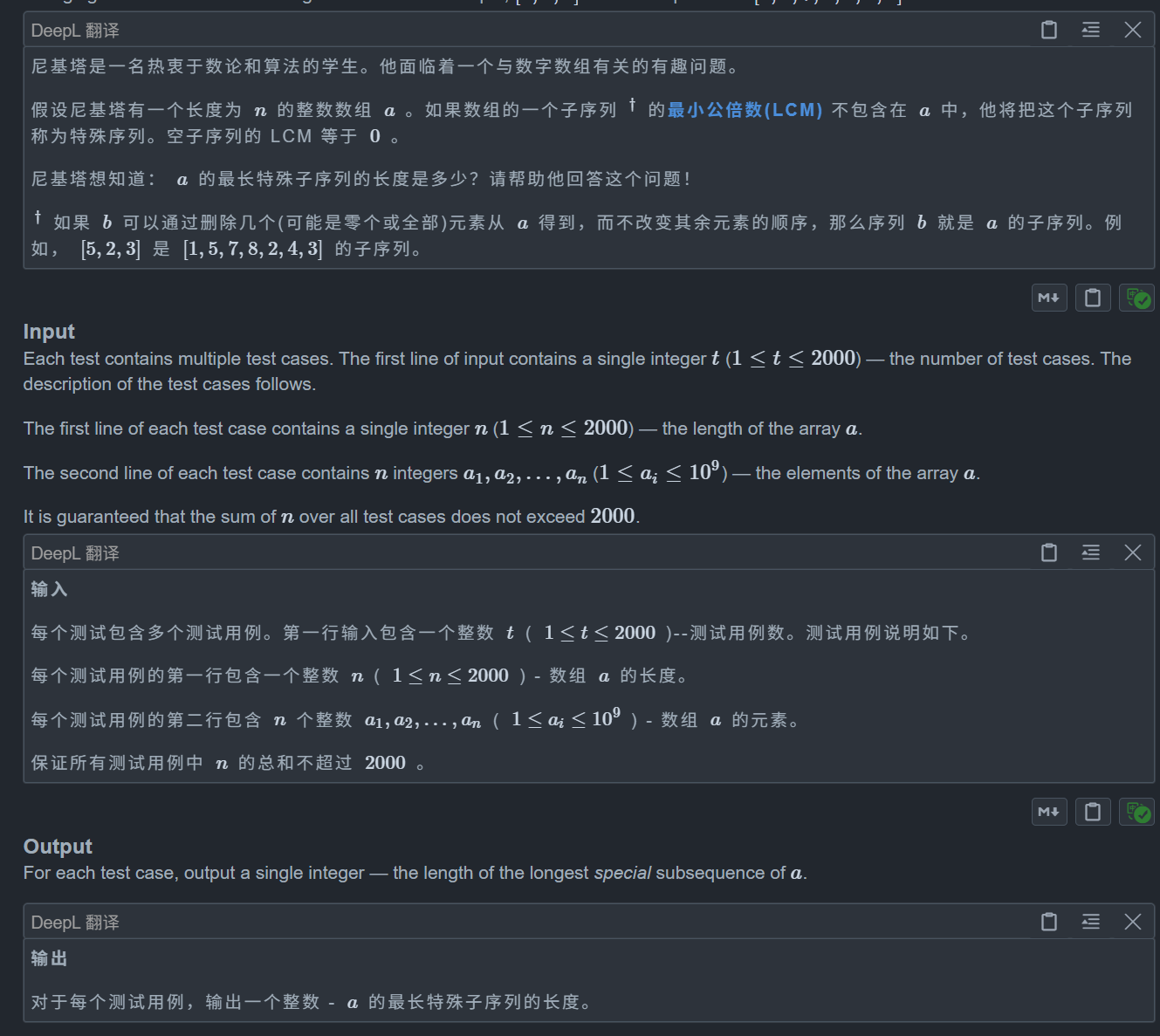

思路：

LCM + 贪心

首先一个显然的想法就是计算所有数的 LCM，如果这个数大于最大值，那么显然是 n，否则这个LCM一定是最大值

那么接下来怎么办呢？这里就要用到我们的一个性质了：

一个序列的任何 子序列的LCM 都是 整个序列LCM 的因数 

因此我们可以枚举最大值的因数来当作答案，那么遍历数组我们只需要看这个数是不是我们当前这个LCM的因数即可，如果是那么就加入，否则就不加入，由于题目要求最多，所以这个贪心是没问题的，同时由于这个因数可能之前就存在了，所以还要判断一下

特别注意：我们还要存一个暂时的 LCM，如果最后选完的 LCM 不等于我们现在枚举的因数，那么就不行，为什么这样贪心可以呢？我的想法是由于我们枚举了所有的因数，如果算出来的 LCM 不是现在枚举的因数，那么可能会被更大的因数给夺舍，即有另外的因数能承受这个 LCM

代码：

#include using namespace std;#define int long long#define yes cout << \"Yes\\n\"#define no cout <> n; vector a(n); int mxlcm = 1; map mp; for (int i = 0; i > a[i]; mp[a[i]]++; } int mx = *max_element(a.begin(), a.end()); for (int i = 0; i  mx) { cout << n << endl; return; } } int ans = 0; auto update = [&](int factor) { int temp = 0; int LCM = 1; if (mp.count(factor)) return; for (auto& [b,cnt] : mp) { if (factor % b == 0) temp+=cnt,LCM = lcm(LCM,b); } if(LCM != factor) return; ans = max(ans, temp); }; for (int i = 1; i * i <= mx; i++) { if (mx % i == 0) { update(i); update(mx / i); } } cout << ans <> t; while (t--) { solve(); } return 0;}

F1. Omsk Metro (simple version)

题目：

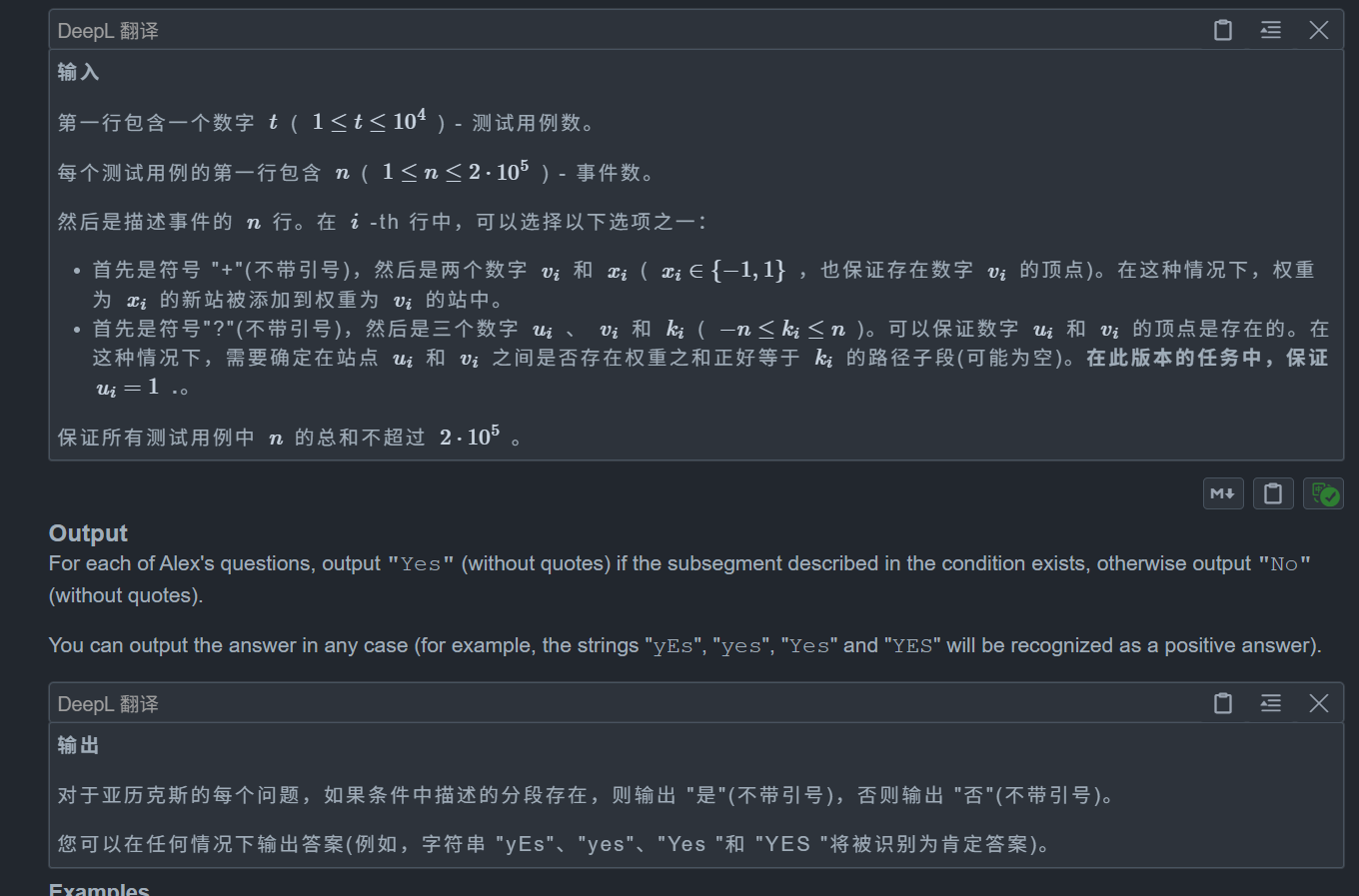思路：

很有意思的一题，考察观察性质

对于这道题我们其实可以离线处理询问，所以我们不妨假设已经知道图了

观察到节点的权值只能是 1 -1，所以我们来探讨是否有什么性质，手玩一下即可发现，对于一个全是 -1 1 的数组，如果其最大字段和是 mx，最小字段和是 mi，那么只要 k = mi，那么 k 就能被构造出来（这个特点遇到其他 -1 1 权值时也可探讨一下是不是这样）

所以我们将数组变为树即可，然后进行一个简单的DP就行了

代码：

#include using namespace std;#define yes cout << \"YES\\n\"#define no cout <> n; int sz = 1; val[sz] = 1; vector mi(n + 5, 0), mx(n + 5, 0); vector<vector> g(n + 5); vector<tuple> ask; for (int i = 1; i > c; if (c == \'+\') { int u, x; cin >> u >> x; sz++; g[u].push_back(sz); g[sz].push_back(u); val[sz] = x; } else { int u, v, k; cin >> u >> v >> k; ask.push_back({u, v, k}); } } auto dfs = [&](auto &&self, int fa, int se) -> void { if (se == 1) { // 特判 mx[se] = 1; mi[se] = 0; } else { mx[se] = max(mx[fa] + val[se], val[se]); mi[se] = min(mi[fa] + val[se], val[se]); } for (auto &son : g[se]) { if (son == fa) continue; self(self, se, son); } }; auto dfs2 = [&](auto &&self, int fa, int se) -> void { mx[se] = max(mx[fa], mx[se]); mi[se] = min(mi[fa], mi[se]); for (auto &son : g[se]) { if (son == fa) continue; self(self, se, son); } }; dfs(dfs, 0, 1); dfs2(dfs2, 0, 1); for (auto &[a, b, c] : ask) { if (mi[b] = c) { yes;  } else { no; } }}signed main(){ ios::sync_with_stdio(false); cin.tie(nullptr); int t = 1; cin >> t; while (t--) { solve(); } return 0;}