算法训练营day30 贪心算法④ 重叠问题 452. 用最少数量的箭引爆气球、435. 无重叠区间 、 763.划分字母区间

        贪心算法的第四篇博客，主要是重叠问题的练习，思路都较为简单，最后一题可能需要着重思考一下

452. 用最少数量的箭引爆气球

        遍历数组，如果存在重叠则减少一支箭（不重叠则增加一支箭）

        重叠的判定：基于累积的最小重叠区间

class Solution: def findMinArrowShots(self, points: List[List[int]]) -> int: if len(points) == 0: return 0 points.sort(key=lambda x: x[0]) # 默认升序 result = 1 for i in range(1, len(points)): if points[i][0] > points[i - 1][1]: # 气球i和气球i-1不挨着，注意这里不是>= result += 1  else: points[i][1] = min(points[i - 1][1], points[i][1]) # 更新重叠气球最小右边界 return result

435. 无重叠区间 

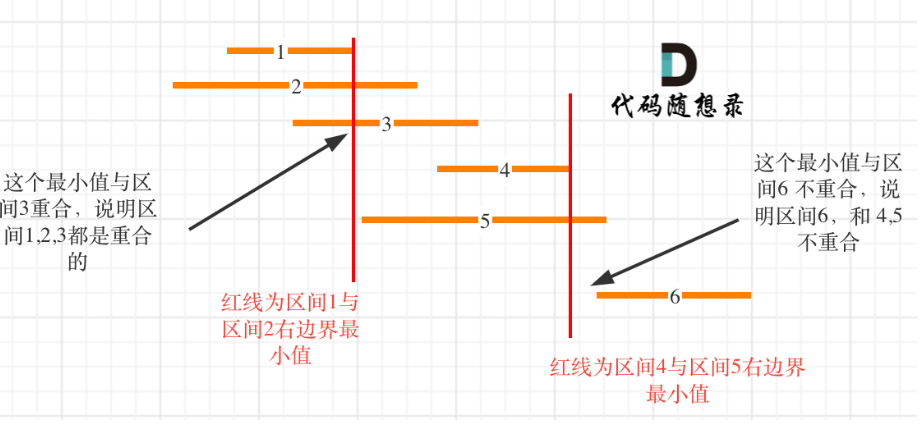
注：图片引用自《代码随想录》

        右排序，遍历左端点，小于则删除（左排序相同思路）

class Solution: def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int: if not intervals: return 0 intervals.sort(key=lambda x: x[0]) # 按照左边界升序排序 count = 0 # 记录重叠区间数量 for i in range(1, len(intervals)): if intervals[i][0] < intervals[i - 1][1]: # 存在重叠区间 intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]) # 更新重叠区间的右边界 count += 1 return count

763.划分字母区间

贪心思路：

• 统计每一个字符最后出现的位置
• 从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

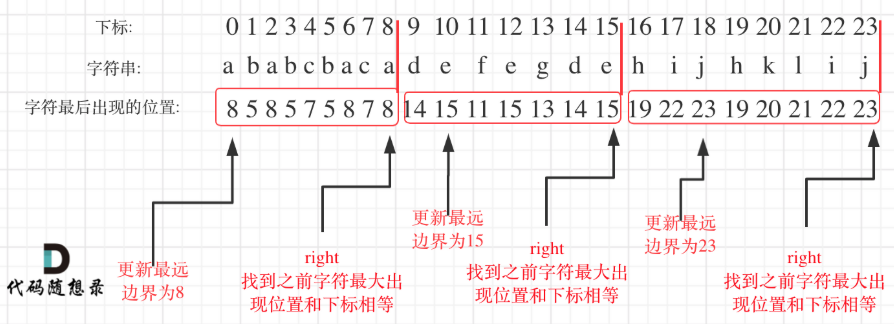
注：图片引用自《代码随想录》

class Solution: def partitionLabels(self, s: str) -> List[int]: last_occurrence = {} # 存储每个字符最后出现的位置 for i, ch in enumerate(s): # 遍历可迭代对象, 生成索引和值 last_occurrence[ch] = i # 重点理解写法 result = [] start = 0 end = 0 for i, ch in enumerate(s): end = max(end, last_occurrence[ch]) # 找到当前字符出现的最远位置 if i == end: # 如果当前位置是最远位置，表示可以分割出一个区间 result.append(end - start + 1) start = i + 1 return result

按照上面两题思路仿写

class Solution: def countLabels(self, s): # 初始化一个长度为26的区间列表，初始值为负无穷 hash = [[float(\'-inf\'), float(\'-inf\')] for _ in range(26)] hash_filter = [] for i in range(len(s)): if hash[ord(s[i]) - ord(\'a\')][0] == float(\'-inf\'): hash[ord(s[i]) - ord(\'a\')][0] = i hash[ord(s[i]) - ord(\'a\')][1] = i # 记录每一个元素的起始位置和结束位置 for i in range(len(hash)): if hash[i][0] != float(\'-inf\'): hash_filter.append(hash[i]) # 按照字母顺序拼接, 刨除空元素 return hash_filter def partitionLabels(self, s): res = [] hash = self.countLabels(s) hash.sort(key=lambda x: x[0]) # 按左边界从小到大排序 rightBoard = hash[0][1] # 记录最大右边界 leftBoard = 0 for i in range(1, len(hash)): if hash[i][0] > rightBoard: # 出现分割点(出现新元素左边界大于现存的最大右边界) res.append(rightBoard - leftBoard + 1) leftBoard = hash[i][0] rightBoard = max(rightBoard, hash[i][1]) # 最大右边界 res.append(rightBoard - leftBoard + 1) # 最右端 return res