网站导航
> 技术文档 > 机器学习 KNN 算法,鸢尾花案例

机器学习 KNN 算法,鸢尾花案例

网友: 技术文档 2025-07-26 20:25:03

目录

一.机器学习概述

二.人工智能的两大方向

三.KNN算法介绍

1.核心思想：“物以类聚，人以群分”

2.算法步骤

四.KNN算法实现

1.安装scikit-learn库

2.导入knn用于分类的类KNeighborsClassifier

3.设置KNeighborsClassifier的相关参数

4.训练模型

5.进行预测

6.计算准确率

五.鸢尾花案例实现

1.准备训练集和测试集数据

2.读取数据

3.划分训练集

4.调用KNN,完成训练过程

5.用训练集中的数据预测，并计算结果的正确率

6.划分测试集

7.将测试集中的数据进行预测，计算准确率

8.完整代码呈现

一.机器学习概述

  • 机器学习是人工智能的核心技术之一，涉及利用数学公式从数据中总结规律。
  • 经典算法（如KNN、线性回归、决策树等）是学习重点，掌握后可轻松扩展至衍生算法。
  • 机器学习流程分为三个阶段：
    • 数据收集：需大量高质量数据（如GPT训练数据达45TB）。
    • 模型训练：通过数学公式求解未知参数（如抛物线公式中的ABC）。
    • 预测：将新数据代入训练好的模型得出结果。

二.人工智能的两大方向

  • 回归：预测连续型数值（如房价、股票价格、温度）。
  • 分类：划分离散类别（如人脸识别、指纹识别、动物分类）。

三.KNN算法介绍

1.核心思想：“物以类聚，人以群分”

KNN 分类的核心逻辑是：一个样本的类别，由它周围距离最近的 K 个邻居的类别决定。

  • 如果一个样本周围的多数邻居属于某一类，则该样本也被判定为该类。
  • 这是一种 “懒惰学习”（Lazy Learning）算法，训练阶段不进行模型拟合，仅存储所有训练数据；直到预测时，才通过计算新样本与训练样本的距离来确定类别。

2.算法步骤

  1. 确定参数 K：选择一个正整数 K（例如 K=3、5、7），表示要参考的 “邻居数量”。

    • K 值过小：容易受噪声影响，模型过拟合（泛化能力差）。
    • K 值过大：可能包含过多其他类别的样本，模型欠拟合（分类模糊）。

  2. 计算距离：对于待预测的新样本，计算它与所有训练样本之间的距离（衡量样本间的 “相似性”）。 常用距离度量方式：

    • 欧氏距离（最常用，适用于连续特征）：
    • 二维空间公式：√[(x₁-x₂)² + (y₁-y₂)²]。
    • 三维空间公式：√[(x₁-x₂)² + (y₁-y₂)² + (z₁-z₂)²]。
    • N维空间扩展：对每个维度差值平方求和后开根号。
    • 曼哈顿距离（适用于高维数据，抗噪声）：\\(\\text{距离} = |x_1-y_1| + |x_2-y_2| + ... + |x_d-y_d|\\)
    • 余弦相似度（适用于文本、向量等，衡量方向相似性）。

  3. 筛选 K 个最近邻：根据距离从小到大排序，选取与新样本距离最近的 K 个训练样本（即 “K 个邻居”）。

  4. 投票决定类别：统计 K 个邻居的类别，出现次数最多的类别即为新样本的预测类别（“少数服从多数”）。

四.KNN算法实现

1.安装scikit-learn库

KNN算法已封装于Scikit-learn（SKL）库中，无需手动实现距离公式和训练过程，所以我们要先安装好scikit-learn库（可以自己指定版本号），命令如下：

 pip install scikit-learn==1.0.2 -i Https://pypi.tuna.tsinghua.edu.cn/simple

2.导入knn用于分类的类KNeighborsClassifier

from sklearn.neighbors import KNeighborsClassifier

3.设置KNeighborsClassifier的相关参数

源码如下：

class KNeighborsClassifier(KNeighborsMixin, ClassifierMixin, NeighborsBase): \"\"\"Classifier implementing the k-nearest neighbors vote. def __init__( self, n_neighbors=5, *, weights=\"uniform\", algorithm=\"auto\", leaf_size=30, p=2, metric=\"minkowski\", metric_params=None, n_jobs=None, ): super().__init__( n_neighbors=n_neighbors, algorithm=algorithm, leaf_size=leaf_size, metric=metric, p=p, metric_params=metric_params, n_jobs=n_jobs, ) self.weights = weights
  • 关键参数：
    • n_neighbors（K值，默认5）：控制邻居数量。
    • weights（权重）：可调整不同类别的优先级（如偏好红色数据）。
    • algorithm（计算算法）：优化排序速度（如暴力搜索、KD树、球树或自动选择）。

4.训练模型

KNeighborsClassifier中已经封装过fit()方法，所以我们只用调用方法即可完成训练过程

knn = KNeighborsClassifier(n_neighbors=5)knn.fit(train_x,train_y)

train_x为训练集中的特征数据

train_y为根据特征而得到的分类类别数据

5.进行预测

可以直接通过KNeighborsClassifier中的predict()方法完成对数据的预测

train_predicted = knn.predict(要预测的数据)

6.计算准确率

可以直接通过KNeighborsClassifier中的score()方法完成对预测数据结果的准确率的计算

train_score = knn.score(train_x,train_y)

五.鸢尾花案例实现

1.准备训练集和测试集数据

鸢尾花训练数据.xlsx 如下：

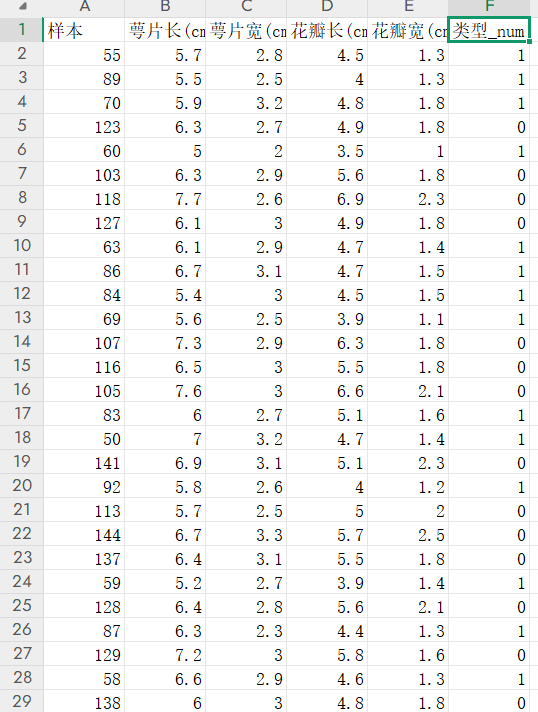
鸢尾花测试数据.xlsx 如下：

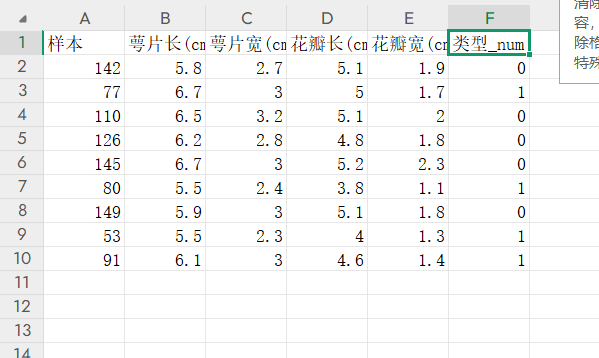
2.读取数据

train_data=pd.read_excel(\'鸢尾花训练数据.xlsx\')test_data=pd.read_excel(\'鸢尾花测试数据.xlsx\')

3.划分训练集

将训练集的特征列划分到train_x数据，分类类型则划分到train_y中

train_x=train_data[[\'萼片长(cm)\',\'萼片宽(cm)\',\'花瓣长(cm)\',\'花瓣宽(cm)\']]train_y=train_data[\'类型_num\']

4.调用KNN,完成训练过程

knn=KNeighborsClassifier(n_neighbors=5)knn.fit(train_x,train_y)

5.用训练集中的数据预测，并计算结果的正确率

train_predicted = knn.predict(train_x)train_score = knn.score(train_x,train_y)print(\'train_score={}\'.format(train_score))train_score=0.9696969696969697

可以看到，即使使用训练集中的数据进行预测，也达不到百分百的正确率

6.划分测试集

test_x=test_data[[\'萼片长(cm)\',\'萼片宽(cm)\',\'花瓣长(cm)\',\'花瓣宽(cm)\']]test_y=test_data[\'类型_num\']

7.将测试集中的数据进行预测，计算准确率

test_predicted=knn.predict(test_x)test_score = knn.score(test_x,test_y)print(\'test_score={}\'.format(test_score))test_score=1.0

由于测试集中数据比较少，所以正确率达到了百分百

8.完整代码呈现

from sklearn.neighbors import KNeighborsClassifierimport pandas as pdtrain_data=pd.read_excel(\'鸢尾花训练数据.xlsx\')test_data=pd.read_excel(\'鸢尾花测试数据.xlsx\')train_x=train_data[[\'萼片长(cm)\',\'萼片宽(cm)\',\'花瓣长(cm)\',\'花瓣宽(cm)\']]train_y=train_data[\'类型_num\']knn=KNeighborsClassifier(n_neighbors=5)knn.fit(train_x,train_y)train_predicted = knn.predict(train_x)train_score = knn.score(train_x,train_y)print(\'train_score={}\'.format(train_score))test_x=test_data[[\'萼片长(cm)\',\'萼片宽(cm)\',\'花瓣长(cm)\',\'花瓣宽(cm)\']]test_y=test_data[\'类型_num\']test_predicted=knn.predict(test_x)test_score = knn.score(test_x,test_y)print(\'test_score={}\'.format(test_score))
网络标签：

相关问题