2025华中杯数学建模B题完整分析论文（共42页）（含模型、数据、可运行代码）_2024华中杯b题优秀论文

2025华中杯大学生数学建模B题完整分析论文

目录

一、问题重述 

二、问题分析 

三、模型假设 

四、 模型建立与求解 

4.1问题1 

4.1.1问题1解析 

4.1.2问题1模型建立 

4.1.3问题1样例代码（仅供参考） 

4.1.4问题1求解结果（仅供参考） 

4.2问题2 

4.2.1问题2解析 

4.2.2问题2模型建立 

4.2.3问题2样例代码（仅供参考） 

4.2.4问题2求解结果（仅供参考） 

4.3问题3 

4.3.1问题3解析 

4.3.2问题3模型建立 

4.3.3问题3样例代码（仅供参考） 

4.3.4问题3求解结果（仅供参考） 

4.4问题4 

4.4.1问题4解析 

4.4.2问题4模型建立 

4.4.3问题4样例代码（仅供参考） 

4.4.4问题4求解结果(仅供参考） 

五、 模型推广 

2025华中杯B题助攻资料下载链接: https://pan.baidu.com/s/1yfeLeOfOBU37A9UvDMECzg提取码: cdr6 复制这段内容后打开百度网盘手机App，操作更方便哦https://pan.baidu.com/s/1yfeLeOfOBU37A9UvDMECzg

摘  要

随着共享单车在校园场景中的普及，其便利性逐渐显现，但同时也暴露出调度不及时、点位分布不合理、运维效率低等问题。为解决上述问题，本文以某高校校园共享单车的运营数据为基础，围绕单车的分布特征、调度策略、点位优化和故障回收四个方面进行系统建模与分析，构建一套完整的校园共享单车运营优化方案。

在问题一中，我们基于附件1提供的调查数据，结合学校作息时间表与典型晴天时段，对共享单车在各个停车点的数量进行统计与推算。通过时间序列插值、均值平滑等方法，估算出校园内当前的共享单车总量，并构建车辆数量在不同时间与空间点位之间的分布模型。最终形成多时间节点、多站点的单车数量矩阵，为调度模型提供基础数据支持。

在问题二中，我们首先建立各停车点在不同时段的用车需求模型，结合校园作息规律、课表分布与学生流动路径，推导各时间段的用车高峰及低谷分布。进而以最小化高峰期供需差异为目标，构建共享单车调度模型，设定调度车速、载量、数量等约束，规划合理的单车调配方案。利用优化算法求解调度路径和车辆分配计划，实现资源在各站点间的动态平衡，显著缓解高峰期车辆短缺问题。

在问题三中，基于问题二的调度优化结果，我们提出共享单车运营效率评价模型，从单车平均利用率、调度频率、站点响应度等维度设计指标体系，对现有停车点布局进行量化评估。分析结果表明部分区域存在车辆集中或闲置问题，影响运营效率。我们通过聚类与覆盖分析方法，重新划分停车区域，调整停车点位置与数量，提升单车分布的均衡性。调整后再次评估运营效率，验证布局优化效果显著，进一步提升了系统运行性能。

在问题四中，我们考虑单车的每日故障率为6%，建立面向维修效率的巡检优化模型。假设运维人员每日巡检并回收故障车辆，以最短路径最大回收为目标，构建基于旅行商问题（TSP）的优化路径模型，考虑装载限制与操作时间约束，规划出最优的巡检顺序与时间节点。结合问题三中的新布局方案，模拟鲁迪师傅的巡检任务安排，有效压缩故障回收时间，提升检修效率，保障了校园共享单车系统的稳定与可持续运行。

综上所述，本文从数据分析、模型建立到方案优化，形成了覆盖共享单车运营、调度、评价与运维的全流程管理框架，具有较强的现实意义与推广价值，可为高校及其他封闭式区域共享交通管理提供理论支持和实践参考。

关键词：共享单车运营；用车需求预测；调度优化；点位设置；巡检路径规划

2025华中杯B题助攻资料下载链接: https://pan.baidu.com/s/1yfeLeOfOBU37A9UvDMECzg提取码: cdr6 复制这段内容后打开百度网盘手机App，操作更方便哦

一、问题重述

 1：共享单车总量估算与分布分析

随着共享单车在校园内的普及，掌握其总量和分布情况对于后续调度与管理至关重要。题目提供了若干晴朗天气下多个时间点、不同共享单车停车点的实际调查数据。我们需要在数据基础上，估算校园内实际存在的共享单车总数量，同时分析每个时间节点（如早上7点、上午9点、中午12点等）各停车点的单车分布特征。考虑到学生出行高峰主要集中在上下课、就餐和晚自习前后，车辆的动态分布将呈现一定的周期性和规律性。通过建立合理的时间序列模型或回归预测模型，能够推测其他未调查时间段的车辆分布情况，为后续调度建模提供数据支撑。

 2：用车需求建模与高峰期调度优化

共享单车在校园内的使用具有明显的时间规律性，高峰时段常常伴随着局部区域共享单车供不应求的情况。为了提升出行效率并缓解供需矛盾，本问题需要我们基于问题1中得到的单车时空分布情况，进一步构建不同停车点在不同时间段的用车需求模型。我们需要根据学校的作息时间表，结合单车进出变化量，评估每个停车点在关键时间段的潜在用车需求与车辆缺口。在需求模型的基础上，建立一个高效的共享单车调度模型，合理规划3辆调度车的运行路线与调度策略。调度车具有速度限制和运输容量上限，因此在模型设计时需考虑多个约束条件，以在高峰到来前，尽可能将单车从剩余较多的区域调往短缺区域，优化资源配置，提高用户的骑行可达性。

 3：运营效率评价与站点布局优化

共享单车的有效运营不仅取决于总量和调度策略，还与停车点的布局密切相关。合理的站点布局能够减少不必要的调度成本，提高车辆的周转效率。本问题的目标是建立一套可量化的共享单车运营效率评价模型，综合考虑单车使用频率、站点平均利用率、调度成本、车辆周转时间、供需匹配度等指标，评估当前站点设置是否合理。若模型评估结果显示某些站点长期闲置、调度压力过大或位置设置不合理，我们需要提出停车点的优化方案，如调整站点位置、增设新的站点或合并低频率站点等。站点优化后，需再次对新布局进行效率评估，验证其在降低调度压力、提高资源利用率方面的有效性，从而实现系统的良性运转。

 4：故障车辆巡检调度与维修效率提升

随着共享单车使用频率的增加，车辆损坏成为制约运营效率的重要因素之一。题目假设每天有约6%的车辆出现故障，若未及时处理将影响用户骑行体验，甚至造成资源浪费。本问题要求我们在优化后的站点布局基础上，设计故障车辆的巡检与维修方案。鲁迪作为校园唯一的检修师傅，需要在保证维修效率的前提下，合理安排每天的巡检时间和路径。考虑到检修车辆的最大运输容量（20辆）、平均查找和搬运时间（1分钟/辆）以及车速限制（25km/h），本问题可转化为受时间和资源约束下的路径优化问题，类似于旅行商问题（TSP）或车辆路径问题（VRP）。目标是使鲁迪在有限时间内，最大限度地回收并运输故障车辆至东北角的维修站，控制校园内故障车辆的总比例，维持整个系统的正常运行。

二、问题分析

问题1：共享单车总量估算与时空分布分析

本问题的核心在于通过已有的调查数据，估算校园内共享单车的总数量，并进一步分析不同时间段内各停车点的车辆分布情况。由于学生出行时间具有明显的规律性（如早上上课、午饭时间回宿舍、晚上去自习），停车点的车辆数量在一天中呈现动态变化。因此，我们可以通过典型时间段的统计数据进行归纳建模，推测未观测时段或地点的单车数量。同时，结合学校作息时间与使用习惯，有助于建立时间与空间上的共享单车流动规律，为后续调度优化提供基础数据支持。

问题2：高峰期共享单车调度优化

本问题旨在解决高峰时段共享单车“有的地方车多、有的地方车少”的供需不平衡问题。为了尽量缓解这种矛盾，学校计划在高峰期到来之前对车辆进行调度。该问题的重点在于如何基于各站点的用车需求，利用有限的调度车辆，在时间和空间上进行合理调配，使得整体调度效率最优。调度车有数量限制、载量限制、速度限制，因此我们需要建立一个调度优化模型，合理规划每辆车的行驶路线和调度策略，尽可能提升高峰时段的车辆可用率，降低学生等待时间。

问题3：运营效率评价与站点布局优化

共享单车在校园中的运营效率，不仅受到车辆本身使用频率的影响，还与停车点的布局密切相关。本问题要求我们建立一套评价共享单车运营效率的指标体系，例如车辆利用率、调度频次、平均调度距离、供需匹配程度等，并据此判断当前站点设置是否合理。如果发现某些站点利用率低、调度成本高或长期存在供需失衡问题，则需对其进行优化调整，如合并站点、移动位置或增设新站点。最终，通过对优化后的布局进行再评价，检验其在提升运营效率方面的有效性。

问题4：故障车辆巡检路线与维修安排优化

随着车辆使用频率的增加，共享单车的故障问题不容忽视。为保障系统的正常运行，学校需要安排维修人员定期巡检并回收故障车辆。本问题的核心是如何设计一条高效的巡检路线，使维修人员在有限时间内尽可能回收更多故障车，从而控制校园内故障车辆的比例在较低水平。考虑到检修车的速度、运输上限以及每辆车的搬运时间等限制，问题可以转化为一个受限资源下的路径规划问题，需要在多个目标之间寻求平衡：覆盖故障点最多、行驶距离最短、维修效率最高。

2025华中杯B题助攻资料下载链接: https://pan.baidu.com/s/1yfeLeOfOBU37A9UvDMECzg提取码: cdr6 复制这段内容后打开百度网盘手机App，操作更方便哦

三、模型假设

问题1 模型假设：共享单车数量与分布估算

1. 调查数据具有代表性  

   附件1中的单车数量数据采集是在晴朗天气下完成的，假设其能代表校园内共享单车在正常天气下的使用和分布情况。

2. 学生行为稳定性假设  

   假设在同一天内，学生的出行习惯具有规律性，即每个时间段的骑行高峰和低谷相对稳定，车辆流动具有时间可重复性。

3. 校园封闭性假设  

   假设共享单车始终在校园范围内骑行，不存在出校园使用的情况。

2025华中杯B题助攻资料下载链接: https://pan.baidu.com/s/1yfeLeOfOBU37A9UvDMECzg提取码: cdr6 复制这段内容后打开百度网盘手机App，操作更方便哦

4. 停车点数量固定  

   假设目前的停车点位是固定不变的，不考虑新增或删除站点的影响，仅对现有数据进行分析。

问题1部分代码

% File name: bike_distribution_estimate.m

% Purpose: Estimate total number of shared bikes on campus and export results to Excel

% --------------------------

% Step 1: Initialize parameters

% --------------------------

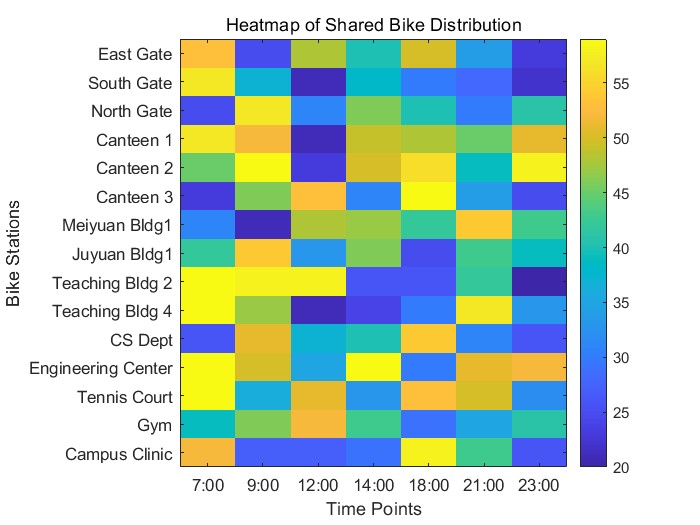
n = 15; % Number of bike stations

m = 7; % Number of time points

% Time labels

time_labels = {\'7:00\', \'9:00\', \'12:00\', \'14:00\', \'18:00\', \'21:00\', \'23:00\'};

% Station labels (can be customized or imported from Excel)

point_labels = {\'East Gate\',\'South Gate\',\'North Gate\',\'Canteen 1\',\'Canteen 2\',\'Canteen 3\',...

\'Meiyuan Bldg1\',\'Juyuan Bldg1\',\'Teaching Bldg 2\',\'Teaching Bldg 4\',...

\'CS Dept\',\'Engineering Center\',\'Tennis Court\',\'Gym\',\'Campus Clinic\'};

% --------------------------

% Step 2: Generate sample data (use real Excel data in practice)

% --------------------------

% Generate random bike counts (range 20–60 bikes per station per time point)

bike_data = randi([20, 60], n, m); % Matrix of size n x m

2025华中杯B题助攻资料下载链接: https://pan.baidu.com/s/1yfeLeOfOBU37A9UvDMECzg提取码: cdr6 复制这段内容后打开百度网盘手机App，操作更方便哦