【DR_CAN-最优控制笔记】04.动态规划_简单的一维案例_动态规划 drcan

目录

文章目录

• 目录
• 系统描述
• • 控制策略1
  • 控制策略2
  • 两种策略比较
• 解析的方法求最优控制策略
• 最优控制策略的具体推导过程
• • 1.分析 J 1 − 2 J_{1-2} J1−2​
  • 2.分析 J 0 − 2 J_{0-2} J0−2​
  • 3.计算最优代价

之前的内容，讨论了动态规划的数值方法求解最优解的过程，这次讨论一个简单的解析方法的例子。

系统描述

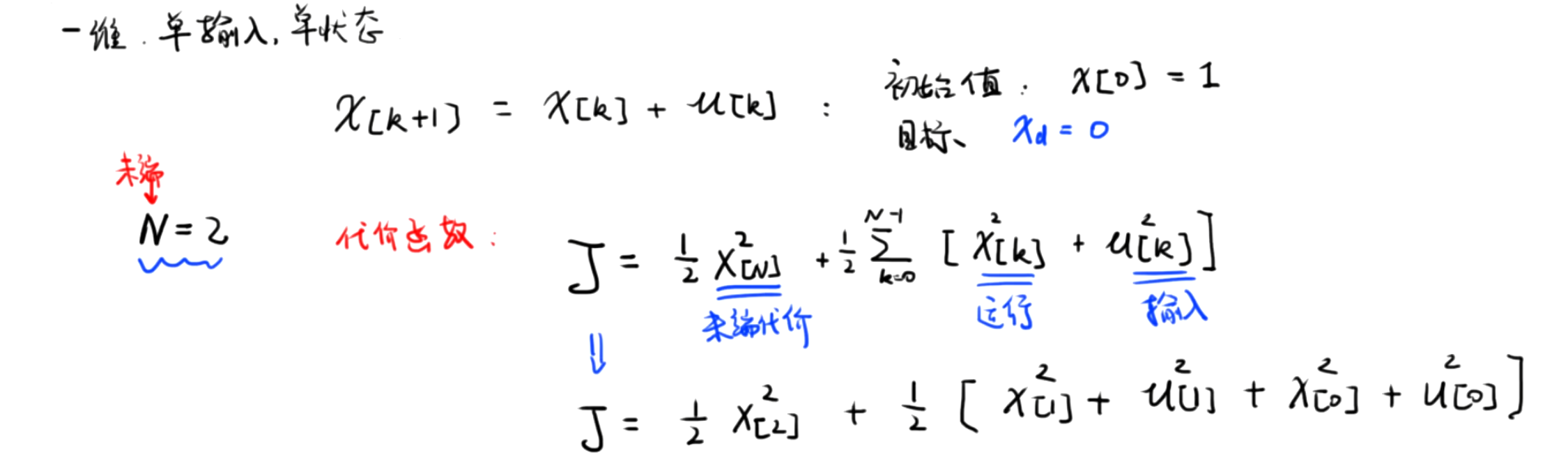
1．为什么 $N=2$ ：在这个案例中，$N$ 表示离散时间的步数，$N=2$ 意味着我们考虑两步的控制过程，即 $u[0]$ 和 $u[1]$ 这两个控制输入，通过这两步输入来控制整个系统的状态。

2．代价函数的形式：代价函数通常包含末端状态代价，运行状态代价和输入状态代价。这是因为我们不仅关心系统最终达到的状态（末端状态代价），还关心系统在运行过程中的状态（运行状态代价）以及控制输入的大小（输入状态代价）。一个合理的代价函数可以综合考虑这些因素，以找到最优的控制策略。

控制策略1

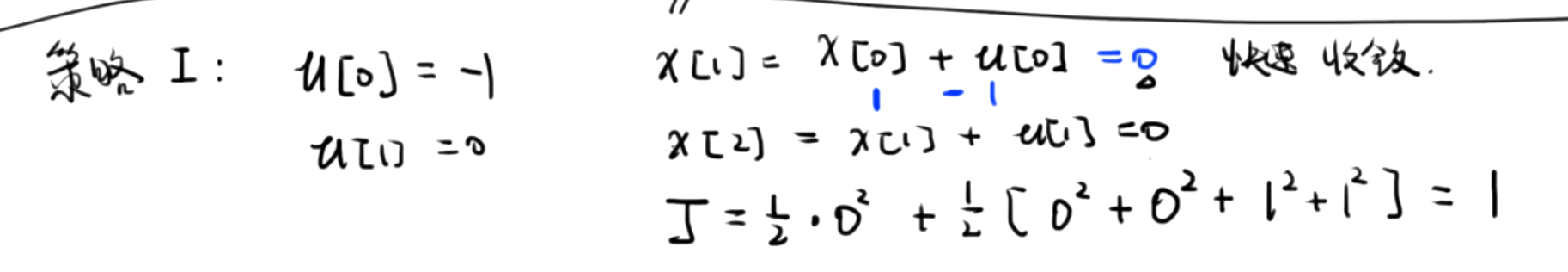
控制策略2

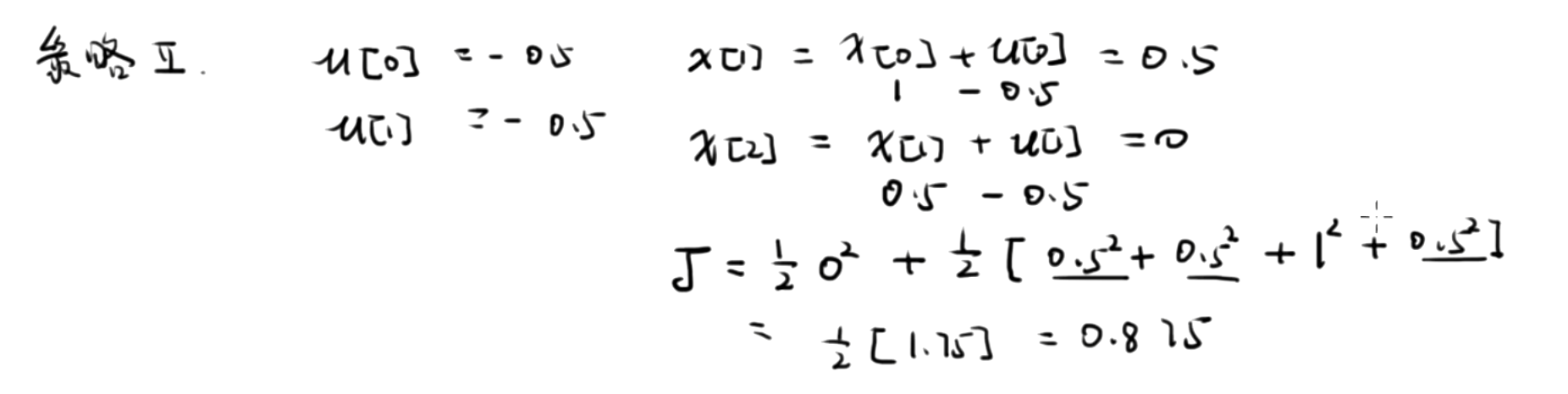
两种策略比较

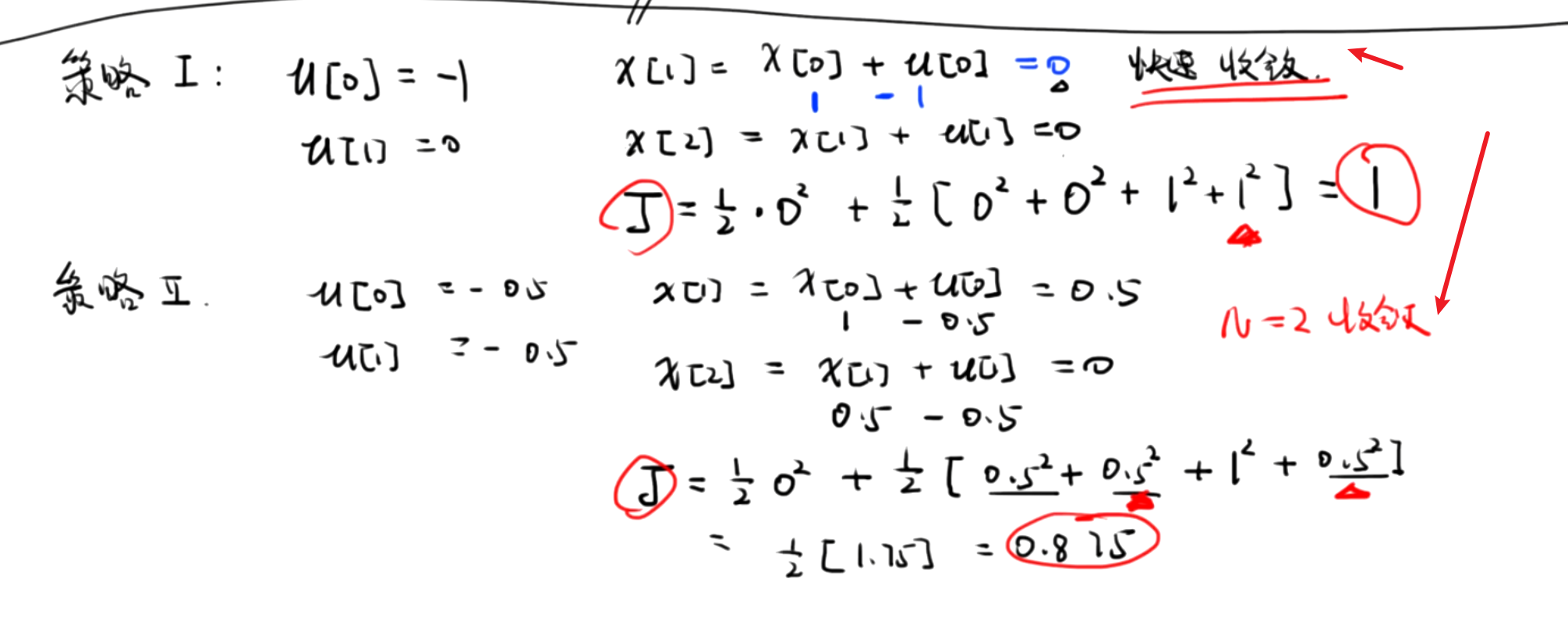
[!NOTE]

​ 一个策略试快速收敛，一个策略是代价小

解析的方法求最优控制策略

[!NOTE]

​ 要找到最优控制量 u ∗ [ 0 ] , u ∗ [ 1 ] u^{*}[0],u^{*}[1] u∗[0],u∗[1] .来促使$J$最小。前面讲解了贝尔曼方程和动态规划的原理，现在使用这些工具进行求解。

[!NOTE]

​ 到这一步，可以看到 J 1 − 2 J_{1-2} J1−2​是跟k=1时的控制输入强相关的。所以到这一步的话，现在的目标就变成了要找到最优的控制输入u[1],使得 m i n ( J 1 − 2) min(J_{1-2}) min(J1−2​)

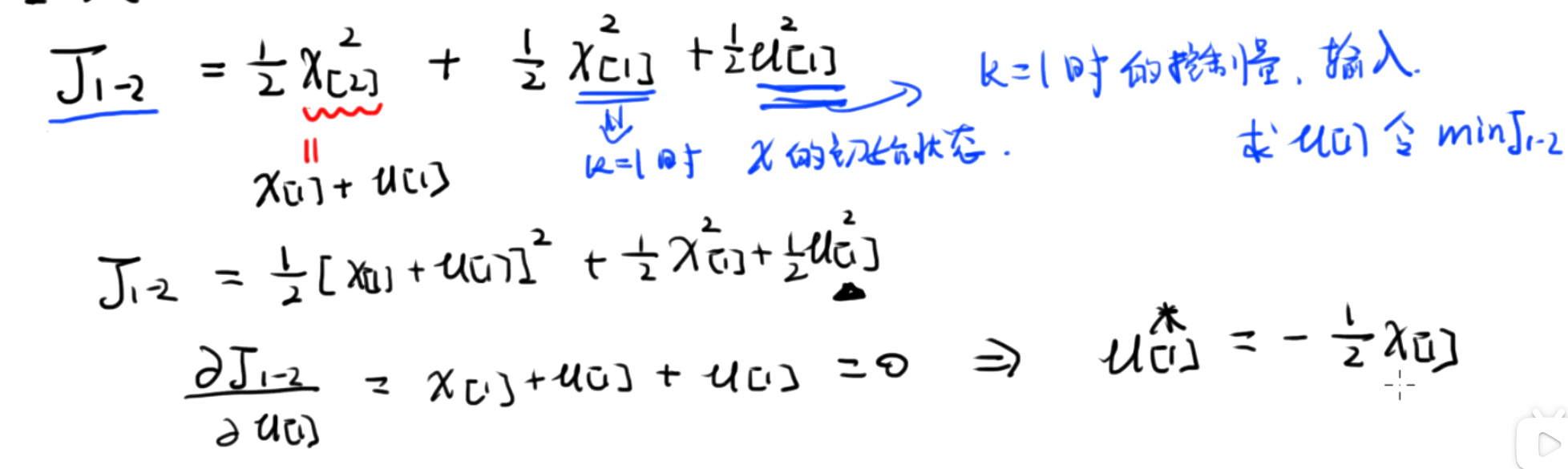
[!NOTE]

​ 将x[2]用x[1]+u[1]替换下来，然后现在J是一个只跟u[1]和x[1]相关的函数，为了找到最小化的J，可以对u[1]求导，然后就能得到最优的u[1]。

​ 有了最优的控制输入u[1],就可以求得这一级的最优剩余代价。

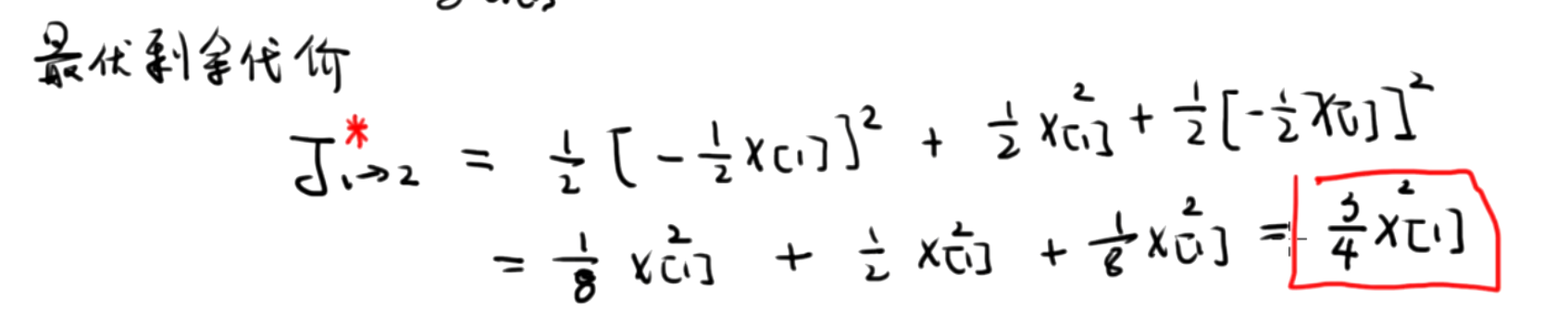
​ 然后分析 J 0 − 2 J_{0-2} J0−2​.

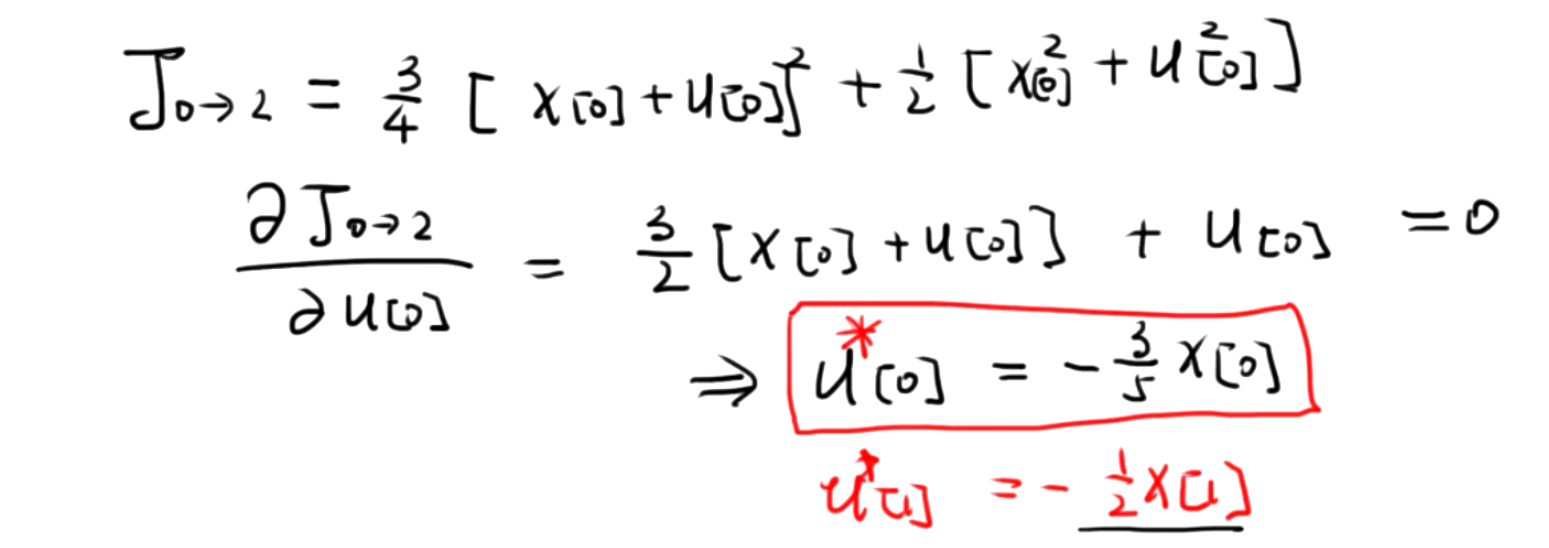
[!NOTE]

​ 从 J 0 − 2 J_{0-2} J0−2​的公式中，可以看出来，包含了一部分 J 1 − 2 J_{1-2} J1−2​的内容，根据最优理论，此处 J 1 − 2 J_{1-2} J1−2​也是最优的，所以使用 J 1 − 2 ∗ J^{*}_{1-2} J1−2∗​ 来替代。

​ 将x[1]替代后，可以看到 J 0 − 2 J_{0-2} J0−2​的一部分已经是最优了，所以只需要另一部分最优即可，对u[0]求导之后，可以得到u[0]的最优量。

​ 有了最优控制量和最优控制策略之后，可以带入相关的值进入J中。

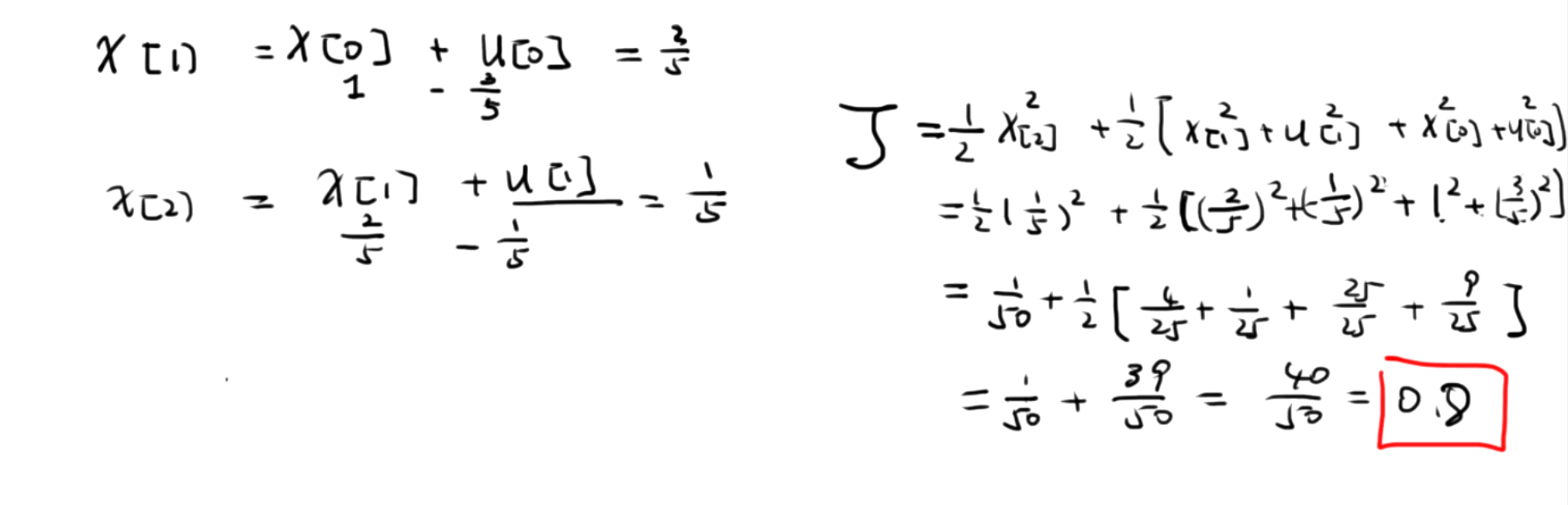
最优控制策略的具体推导过程

1.分析 J 1 − 2 J_{1-2} J1−2​

首先，我们关注 J 1 − 2 J_{1-2} J1−2​ ，它与 $k=1$ 时的控制输入 $u[1]$ 强相关。我们的目标是找到最优的控制输入 $u[1]$ ，使得 J 1 − 2 J_{1-2} J1−2​ 最小，即 min⁡ ( J 1 − 2) \\min \\left(J_{1-2}\\right) min(J1−2​) 。

假设系统的状态转移方程为 $x[k+1]=x[k]+u[k]$ ，那么 $x[2]=x[1]+u[1]$ 。将 $x[2]$ 用 $x[1]+u[1]$ 替换到 J 1 − 2 J_{1-2} J1−2​ 的表达式中，此时 J 1 − 2 J_{1-2} J1−2​ 变成了一个只与 $u[1]$ 和 $x[1]$ 相关的函数，记为 J 1 − 2 (u[1],x[1]) J_{1-2}(u[1], x[1]) J1−2​(u[1],x[1]) 。为了找到 J 1 − 2 J_{1-2} J1−2​ 的最小值，我们对 $u[1]$ 求导，并令导数为 0 ：
∂ J 1 − 2 ( u [ 1 ] , x [ 1 ] ) ∂ u [ 1 ]= 0 \\frac{\\partial J_{1-2}(u[1], x[1])}{\\partial u[1]}=0 ∂u[1]∂J1−2​(u[1],x[1])​=0

解这个方程，就可以得到最优的 $u[1]$ ，记为 u ∗ [1] u^*[1] u∗[1] 。

有了最优的控制输入 u ∗ [1] u^*[1] u∗[1] ，我们就可以求得这一级的最优剩余代价 J 1 − 2 ∗ J_{1-2}^* J1−2∗​ ，即 J 1 − 2 ∗ = J 1 − 2 ( u ∗ [ 1 ] , x [ 1 ] ) J_{1-2}^*=J_{1-2}\\left(u^*[1], x[1]\\right) J1−2∗​=J1−2​(u∗[1],x[1]) 。

2.分析 J 0 − 2 J_{0-2} J0−2​

接下来，我们分析 J 0 − 2 J_{0-2} J0−2​ 。从 J 0 − 2 J_{0-2} J0−2​ 的公式中，可以看出它包含了一部分 J 1 − 2 J_{1-2} J1−2​ 的内容。根据最优性原理，在求解 J 0 − 2 J_{0-2} J0−2​ 的最优解时， J 1 − 2 J_{1-2} J1−2​ 也应该是最优的，所以我们使用 J 1 − 2 ∗ J_{1-2}^* J1−2∗​ 来替代 J 1 − 2 J_{1-2} J1−2​ 。

同样，假设系统的状态转移方程为 $x[1]=x[0]+u[0]$ ，将 $x[1]$ 用 $x[0]+u[0]$ 替换到 J 0 − 2 J_{0-2} J0−2​ 的表达式中，此时 J 0 − 2 J_{0-2} J0−2​ 变成了一个只与 $u[0]$ 和 $x[0]$ 相关的函数，记为 J 0 − 2 (u[0],x[0]) J_{0-2}(u[0], x[0]) J0−2​(u[0],x[0]) 。

由于 J 0 − 2 J_{0-2} J0−2​ 的一部分（即 J 1 − 2 ∗ J_{1-2}^* J1−2∗​ ）已经是最优的，所以只需要让另一部分关于 $u[0]$ 的部分最优即可。我们对 $u[0]$ 求导，并令导数为 0 ：
∂ J 0 − 2 ( u [ 0 ] , x [ 0 ] ) ∂ u [ 0 ]= 0 \\frac{\\partial J_{0-2}(u[0], x[0])}{\\partial u[0]}=0 ∂u[0]∂J0−2​(u[0],x[0])​=0

解这个方程，就可以得到最优的 $u[0]$ ，记为 u ∗ [0] u^*[0] u∗[0] 。

3.计算最优代价

有了最优控制量 u ∗ [0] u^*[0] u∗[0] 和 u ∗ [1] u^*[1] u∗[1] 以及最优控制策略之后，我们可以将相关的值代入 $J$ 中，计算出最优代价 J ∗ J^* J∗ ：
J ∗ = J ( u ∗ [ 0 ] , u ∗ [ 1 ] , x [ 0 ] ) J^*=J\\left(u^*[0], u^*[1], x[0]\\right) J∗=J(u∗[0],u∗[1],x[0])