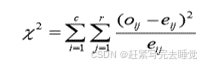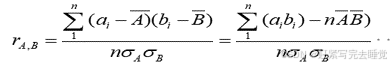数学建模入门——数据预处理(全)_数学建模数据预处理怎么写
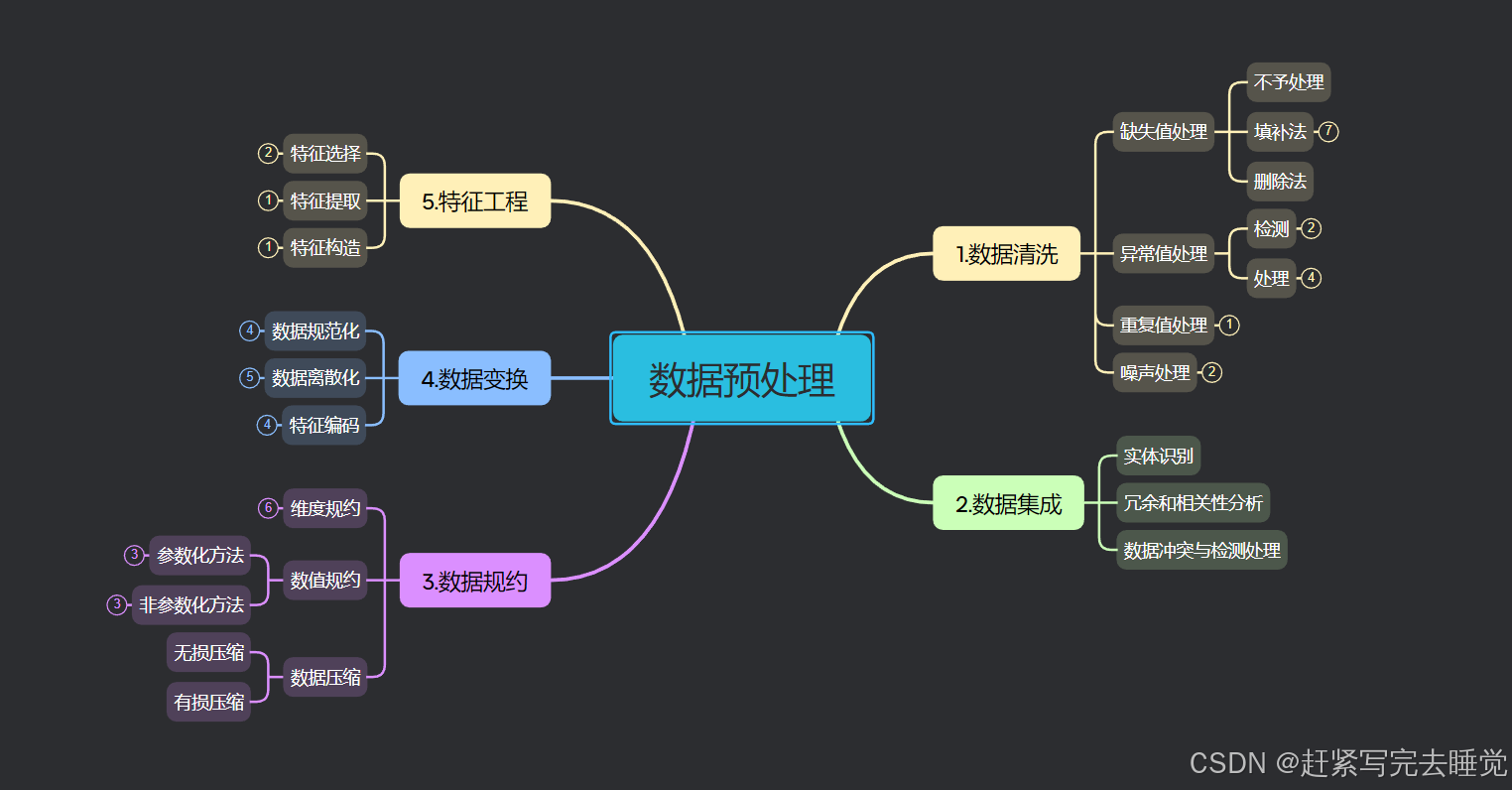
摘要:本篇博客主要讲解了数学建模入门的数据预处理知识和常用方法,涵盖数据清洗、数据集成、数据规约和数据变换,并在最后对特征工程进行了简单的介绍。内容较长,建议收藏后阅读
目录
一、数据预处理概述
二、数据清洗
2.1缺失值处理
2.2异常值处理
2.3重复值处理
2.4噪声处理
三、数据集成
3.1实体识别
3.2冗余性和相关性分析
3.3数据冲突与检测处理
四、数据规约
4.1维度规约
4.2数值规约
4.3数据离散化
4.4数据压缩
五、数据变换
5.1数据规范化
5.2数据离散化
5.3特征编码
六、特征工程
一、数据预处理概述
核心要点:
- 数据处理包括:数据采集、数据存储、数据预处理、数据分析、数据可视化、决策
- 数据处理中最重要的就是:数据预处理
- 数据预处理目的是提高数据的质量,使得我们能使用更高质量的数据进行后续处理
- 数据预处理包括:数据清洗、数据集成、数据规约、数据变换
参考内容:【数据处理】数据预处理·数据规约-CSDN博客
数据清洗:去除重复数据、处理缺失值、去除异常值等。
数据集成:将来自不同数据源的数据进行整合,例如将不同表格中的数据进行合并。
数据规约:对数据进行压缩、抽样等处理,以便于存储和处理。
数据变换:将数据从一种格式转换为另一种格式,例如将文本数据转换为数值型数据。
二、数据清洗
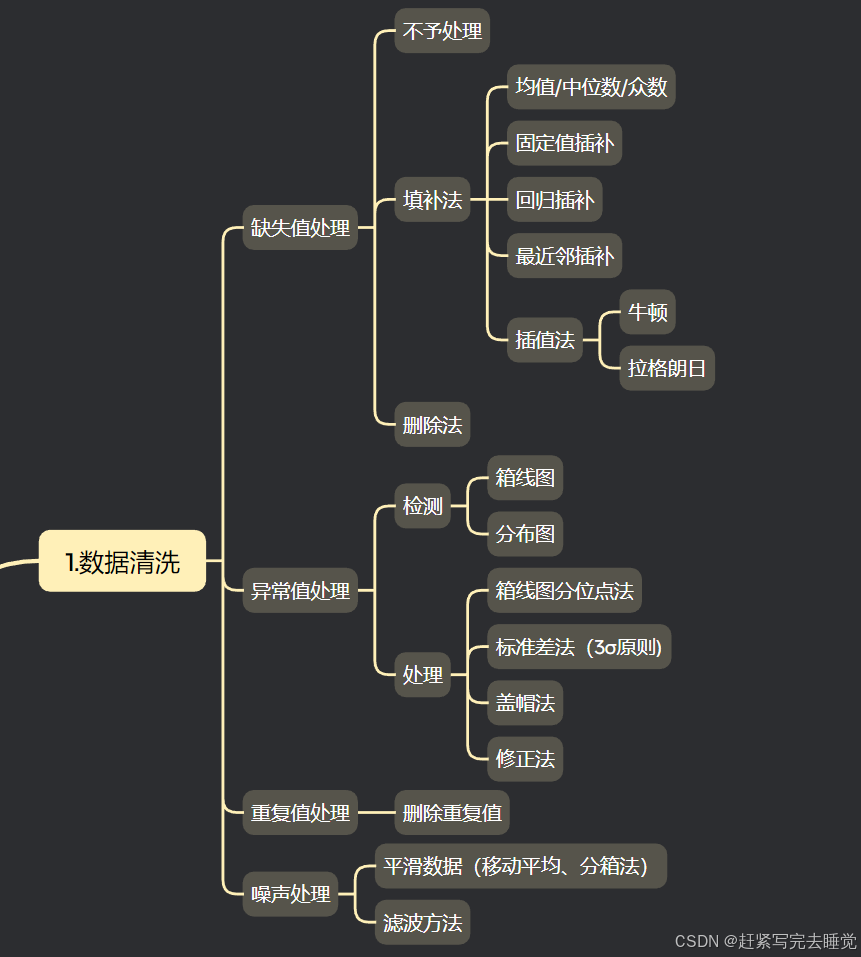
数据清洗是指对采集到的原始数据进行审查和校验的过程,目的是纠正其中的错误、去除重复及无效的数据、补充缺失值等,从而提高数据质量,使其更适合后续的数据分析、挖掘。
2.1缺失值处理
数据清洗包含多项操作,其中缺失值处理是比较重要的一种。
试想一下,一个数据集若是存在重复值、异常值或者其他噪声,就算建立的模型不够精确,尚且还可建立模型进行求解;但若是存在重要特征的缺失值,连建立模型都寸步难行。
- 不予处理:若非重要特征,缺失值虽然影响模型的性能,但是不妨碍数据的建模(有一些模型可能要求不能含有缺失值,还是要视情况而定)。如果你的缺失值占比小,或者缺失值所在的特征对模型影响不大,可以考虑不予处理。
- 删除法:当你的数据量较大或者缺失值的这条数据对模型影响程度很小,可以考虑直接删除这条数据。例如:在Python中可以使用df.dropna()函数对存在缺失特征的数据进行删除。
- 填补法:均值/中位数/众数插补、固定值插补、最近邻插补、回归方法插补、插值法插补
其他填补法描述,具体参考:数据预处理,插值拟合及回归分析_三样条插值法 缺失值-CSDN博客
Python中的使用:#使用feature统计值对NA进行填充df[\'feature\'].fillna(df[\'feature\'].mean()) #均值插补df[\'feature\'].fillna(df[\'feature\'].median()) #中位数插补df[\'feature\'].fillna(df[\'feature\'].mode()) #众数插补
2.2异常值处理
异常值是指那些偏离正常范围的值,不是错误值,比如在调查睡眠时间时,问卷中有90都集中在5-9小时,但是存在极少睡2小时或18小时的,这时就可以将其视为异常值。
- 异常值出现频率较低,但又会对实际项目分析造成偏差
- 异常值一般用过箱线图法(分位差法)或者分布图(标准差法)来判断
- 异常值往往采取盖帽法或者数据离散化
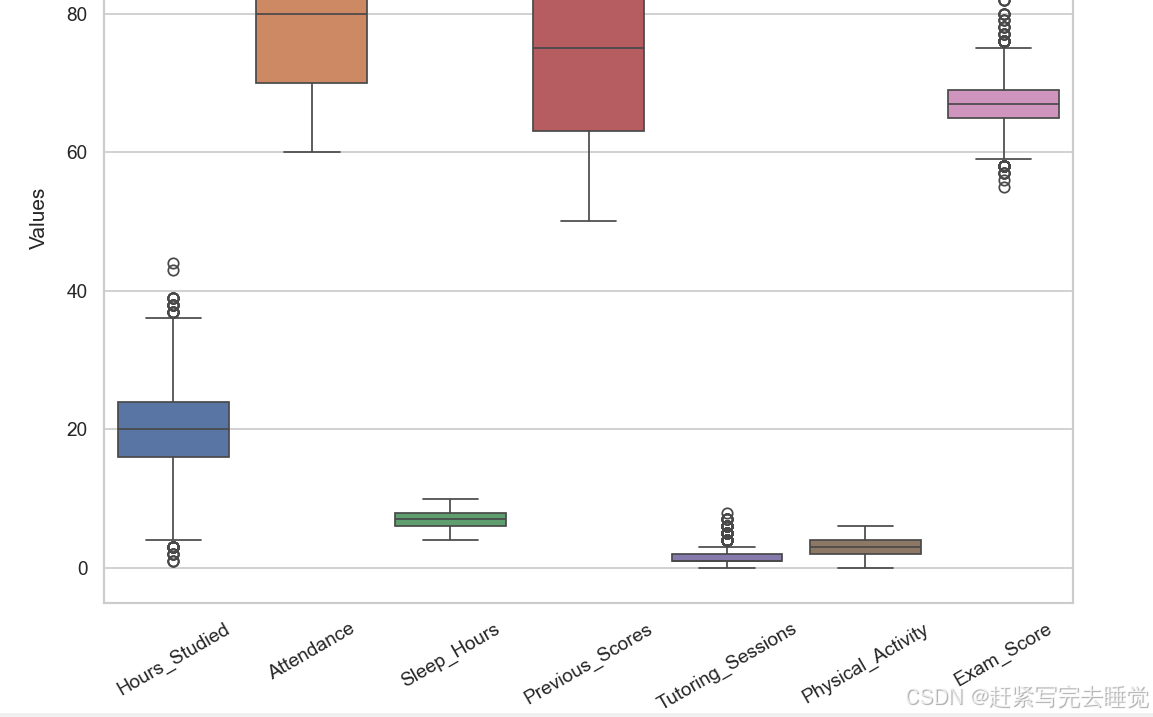
异常值检测:一般地异常值检测方法可用箱线图和分布图来查看。
箱线图:
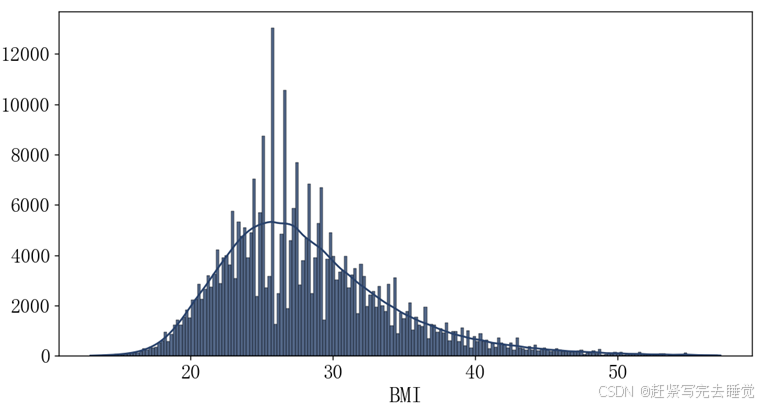
分布图:
异常值处理:常见的有分位点(箱线图)法、标准差法、盖帽法和修正法,其他的基于聚类的方法、孤立森林法等。
- 不予处理:跟缺失值一样,不处理同样可以建模,但是会影响模型的性能,不推荐
- 分位点法:通过箱线图的四分之一分位点和四分之三分位点对异常值进行删除
# 定义函数除去异常值,以IQR方法为例def remove_outliers(df, columns): for col in columns: q1 = df[col].quantile(0.25) q3 = df[col].quantile(0.75) iqr = q3 - q1 lower_bound = q1 - 1.5 * iqr upper_bound = q3 + 1.5 * iqr df = df[(df[col] >= lower_bound) & (df[col] <= upper_bound)] return df
- 标准差法:通过数据分布的标准差进行异常值的删除
\"\"\"使用标准差法去除数据框中指定列的异常值。参数:df (pandas.DataFrame): 包含数据的DataFrame。columns (list): 需要去除异常值的列名列表。\"\"\"def remove_outliers(df, columns): for col in columns: mean_value = df[col].mean() # 计算列的均值 std_value = df[col].std() # 计算列的标准差 lower_bound = mean_value - 3 * std_value # 设定下限(均值 - 3倍标准差) upper_bound = mean_value + 3 * std_value # 设定上限(均值 + 3倍标准差) df = df[(df[col] >= lower_bound) & (df[col] <= upper_bound)] return df
- 盖帽法:可以看做是分位点法的泛化版,根据自己定义的上下限值进行删除
\"\"\"使用盖帽法去除数据框中指定列的异常值。参数:df (pandas.DataFrame): 包含数据的DataFrame。columns (list): 需要去除异常值的列名列表。lower_limits (list): 对应columns中各列数据的下限值列表。upper_limits (list): 对应columns中各列数据的上限值列表。\"\"\"def remove_outliers(df, columns, lower_limits, upper_limits): for col, lower_limit, upper_limit in zip(columns, lower_limits, upper_limits): df[col] = df[col].apply(lambda x: lower_limit if x upper_limit else x)) return df
- 修正法:将异常值看做缺失值,使用缺失值填补的方法对异常值进行修正
其他补充及可参考:异常值处理技巧-CSDN博客,数据预处理——数据清洗_数学建模大赛
2.3重复值处理
重复数据一般不会对模型产生较大影响,有时我们甚至还会人为的制造重复数据,比如当分类模型的目标变量类别不平衡时,我们对类别较少的一方进行随机过采样(有放回的抽取数据)。重复数据也有一些危害,比如浪费计算资源等。是否删除重复值要权衡其中的益弊。
注:有些特殊的重复值不可删除!!!如重复的订单记录!!!
处理重复值的方法很简单,删除多余重复数据,以Python为例:数据清洗:重复值识别和处理方法_重复数据清洗-CSDN博客
#df.drop_duplicates()方法中有两个参数subset和keep。#subset:要判断是否重复的列。可以指定某个列或多个列。默认使用全部列。#keep:表示重复时不标记为True的规则。可指定为first(除第一个重复值外均标记为True)、last(除最后一个重复值外均标记为True)和False(重复值全部标记为True)。默认使用first。 print(df.drop_duplicates()) # 判断所有列值重复的记录,保留重复的第一个值print(df.drop_duplicates(keep=\'last\')) # 判断所有列值重复的记录,保留重复的最后一个值print(df.drop_duplicates(keep=False)) # 判断所有列值重复的记录,删除所有重复的值 print(df.drop_duplicates([\'col2\'])) # 判断col2列值重复的记录,保留重复的第一个值print(df.drop_duplicates([\'col1\', \'col2\'])) # 判断col1、col2列值重复的记录,保留重复的第一个值
2.4噪声处理
噪声是指数据中存在的随机错误或偏差,它会使数据偏离真实情况。不同于异常值,噪声主要是数据采集设备的精度限制、测量环境的干扰等造成的。
常见的噪声处理方法有:平滑数据(移动平均处理、分箱处理)和滤波方法。对于一般地数学建模不用过多的考虑噪声。这里有一个噪声处理的例子可以帮助大家理解:
数据建模的数据清洗:处理缺失值和噪声-CSDN博客
三、数据集成
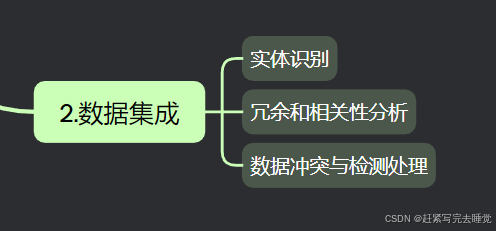
数据集成,即把多个同源或不同源的数据集合并在一个数据集中。在数据集成过程中有一些我们需要注意的关键问题。
3.1实体识别
实体识别问题就是说:你如何确定你合并的两条记录是描述的同一个样本呢?
实体识别问题是数据集成中的首要问题,因为来自多个信息源的现实世界的等价实体才能匹配。如数据集成中如何判断一个数据库中的customer_id和另一数据库中的cust_no是指相同的属性?不同数据源中对于相同的现实世界实体(比如同一客户、同一产品等)可能有着不同的标识方式或记录格式。在数据集成时,需要准确识别出这些代表相同实体的数据,以便将相关的数据进行正确整合。例如,在一个电商系统中,客户在移动端和网页端可能有着不同的用户编号,但实际上指向的是同一个用户,就需要通过一定规则(如手机号、邮箱等唯一标识信息)来识别出这是同一个实体,进而合并相关数据。
3.2冗余性和相关性分析
冗余是数据集成的另一重要问题。如果一个属性能由另一个或另一组属性值“推导”出,则这个属性可能是冗余的。属性命名不一致也会导致结果数据集中的冗余。
有些冗余可以被相关分析检测到,对于标称属性,使用卡方检验,对于数值属性,可以使用相关系数(correlation coefficient)和协方差( covariance)评估属性间的相关性。
(1)标称数据的卡方相关检验
(2)数值数据的相关系数
(3)数值数据的协方差
3.3数据冲突与检测处理
数据集成还涉及数据值冲突的检测与处理。例如不同学校的学生交换信息时,由于不同学校有各自的课程计划和评分方案,同一门课的成绩所采取的评分分数也有可能不同,如十分制或百分制。这就需要我们针对不同的数据冲突形式进行处理。
详细参考:
【数据科学导论】数据预处理·数据集成_数据预处理数据集-CSDN博客
数据导入与预处理-数据集成_主要用于统一不同数据源的矛盾之处
四、数据规约
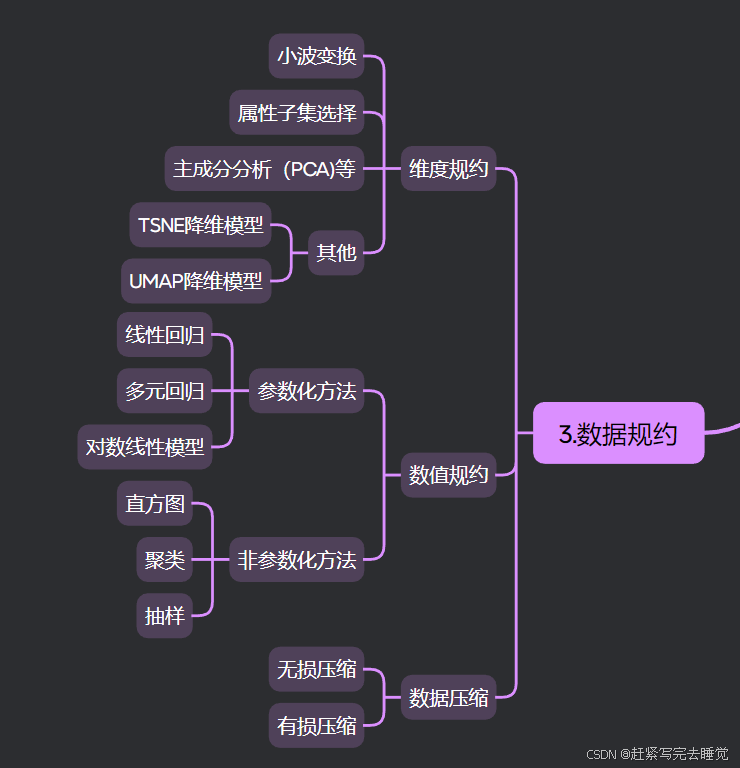
什么是数据规约?
数据规约是指在尽可能保持数据原貌的前提下,通过一定的方法和技术对海量原始数据进行简化处理,以获得更小、更易于管理、分析和处理的数据集合的过程。
为什么要进行数据规约?
在数据清理和集成之后,我们的数据集包含的内容已经比较完整,但是此时数据的规模很大,我们需要减小数据的规模并且最大程度的保留原有数据蕴含的信息。这需要我们进行数据规约。
如何进行数据规约?
数据规约的方式有多种,如:维度规约、数值规约、数据离散化、数据压缩等。
4.1维度规约
维度一般来说就是特征变量或者属性的个数,维度规约就是简化特征变量和属性。
属性子集选择:
从原有的众多属性(变量)中挑选出一部分最有代表性、和分析目标关联性最强的属性组成新的数据集合。例如分析客户购买行为时,从众多客户相关信息属性(如年龄、性别、消费频次、购买时间、居住地址等)里,选出消费频次、年龄等关键属性来进行进一步分析。
小波变换:
小波变换是一种功能强大且应用广泛的信号处理与数据分析方法。主要分为连续小波变换和离散小波变换。连续小波变换在理论分析中较常用,它能对信号进行连续的、精细的时频分析,但计算量相对较大;离散小波变换是连续小波变换经过离散化处理得到的,更适合在实际应用中通过高效的算法实现,便于对数据进行处理、分析以及后续操作。
主成分分析:
通过线性变换将原始的多个相关变量转化为少数几个互不相关的综合变量(主成分),这些主成分能够尽可能多地保留原始数据的方差信息,实现数据的简化,同时又抓住了数据的主要变化特征。与属性子集选择不同的是,属性子集选择是从多个属性中选择部分属性,而主成分是将多个属性转化构造为新的属性。
详细操作请参考:机器学习之主成分分析(PCA)-CSDN博客
4.2数值规约
数值规约是通过选择更小、数据密集度更低的格式来表示数据。数值规约有两种类型 – 基于参数方法和基于非参数方法。参数方法(如回归法)侧重于模型参数,而忽略了数据本身。同样,也可以采用对数线性模型,重点侧重数据中的子空间。而非参数方法(如直方图,可显示数值数据的分布方式)则完全不依赖模型
参数化方法:
参数化数值规约方法是基于一定的数学模型,通过对样本数据进行分析拟合,确定模型中的参数,然后利用这些参数来描述数据整体特征,进而用这些参数代表或简化原始数据的方法。如:线性回归模型、多元回归模型和对数-线性回归模型等。|即构造数学模型来拟合数据而不存储数据(离群点需要特殊存储)
非参数化方法:
非参数化数值规约方法不依赖于数据所服从的特定数学模型以及事先假定的数据分布形式,而是直接从数据本身的特征出发进行数据简化处理的方法。它更关注数据的顺序、位置等关系以及局部特征,能够灵活应对各种复杂的数据分布情况。
例如:直方图、聚类、抽样。直方图通过区间来代表原始数据,聚类通过簇类的中心来代表这一类数据、抽样通过少量的样本来代表总体样本。
4.3数据离散化
数据离散化是指将连续的数据转化为离散的数据,比如:将学生成绩60分以下设置为不及格,60-80设置为良好,80分以上设置为优秀。数据离散化具有数据规约的效果,这个我们将在数据变换中详细讲述。
4.4数据压缩
数据压缩是指通过特定的算法和技术,对原始数据进行处理,以减少其存储空间占用或传输带宽需求等的一种数据规约手段。其目的在于在尽可能保留数据原有价值和关键信息的基础上,让数据以更紧凑的形式存在,方便存储、传输以及后续的处理等操作。
无损压缩:
在无损压缩中,通过编码技术和算法缩减数据大小,并在需要时恢复完整的原始数据,不会有任何的信息丢失。
有损压缩:
有损压缩通过牺牲部分精度来换取更高的压缩比,虽然处理后的数据可能值得保留,但并不像无损压缩那样是一个精确的副本。
五、数据变换
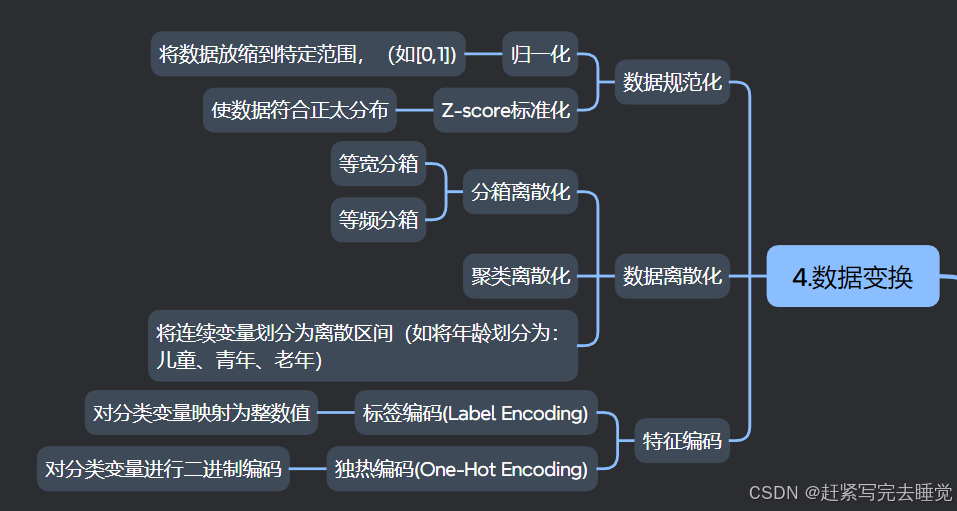
由于原始数据的各特征变量的数据类型和量纲存在差异、不能直接比较,此时就需要进行数据变换。数据变换就是把数据成同一种存在形式,让其可彼此比较。但是数据变化会造成信息损失(如对数变换、分位数变换、离散化)会导致数据的精细信息丢失。特别是分位数变换和离散化会导致数据之间的原始顺序关系或细微差异消失,可能影响模型性能。
初级的数据变换可大致分为:数据规范化、数据离散化、数据二值化和哑变量编码。
5.1数据规范化
数据规范化最常用的两种方法是标准化和归一化。
Z-score标准化:
Z-score标准化也叫标准差标准化又称零均值标准化,是当前使用最广泛的数据标准化方法,其中μ是原数据均值,σ原始数据标准差。经过该方法处理的数据均值为0,标准化为1。
归一化:
归一化是对原始数据所做的一种线性变换,将原始数据的数值映射到[0,1]区间。由于Xmax和Xmin是数据边缘的数据间,所以该变换对离群值很敏感,噪声影响非常大。
小数定标规范化:
其中j是满足
的最小整数。
5.2数据离散化
数据离散化是数据变换环节常用的一种方法,它能将连续型数据转换为离散型数据。主要方法包括:分箱法、聚类离散和决策树离散。
分箱法:
分箱法分为两种,等宽分箱法和等频分箱法。如将不同年龄的人群进行离散化时,使用等宽分箱法,可以将年龄按照每20岁一个区间将[0,100]岁分为5个区间;等频分箱法则是将数据平均分到每个区间,比如[0,100]分为5个区间,那么每个区间的数据是总数据量的1/5。
聚类法:
通过将相似的数据进行聚类将连续的数据进行离散化。每个数据用所在的组别进行代表。
决策树离散化:
构建决策树模型(如 C4.5、CART 等决策树算法),利用决策树对连续属性进行划分,决策树在生长过程中会选择合适的分裂点来区分不同的类别,这些分裂点就可以作为离散化的区间边界。
5.3特征编码
数据预处理中,特征编码用于将类别变量转化为数值型变量。常见的特征编码有标签编码和独热编码。
标签编码(Label Encoding):
将类别型特征的每个不同类别按照一定顺序赋予一个整数标签,例如把 “红色” 标记为 0,“绿色” 标记为 1,“蓝色” 标记为 2 等,通常按照类别出现的自然顺序或者自定义顺序进行编码。
特点:编写简洁、节省空间,但容易给原本没有数值大小关系的类别强加一种顺序关系。
独热编码(One-Hot Encoding):
对于有 n 个类别的类别型特征,会创建 n 个新的二进制特征(取值为 0 或 1)。每一个新特征对应原类别中的一个类别,若样本属于该类别,则对应新特征的值为 1,否则为 0。例如对于颜色特征有 “红”“绿”“蓝” 三个类别,那么经过独热编码后,一个样本如果是 “红” 色,对应的编码就是 [1, 0, 0],如果是 “绿” 色就是 [0, 1, 0] 等。
特点:消除了顺序的影响,便于模型理解,但是当类别数量太多时,会产生大量稀疏矩阵,存储效率低,占空间大。
六、特征工程
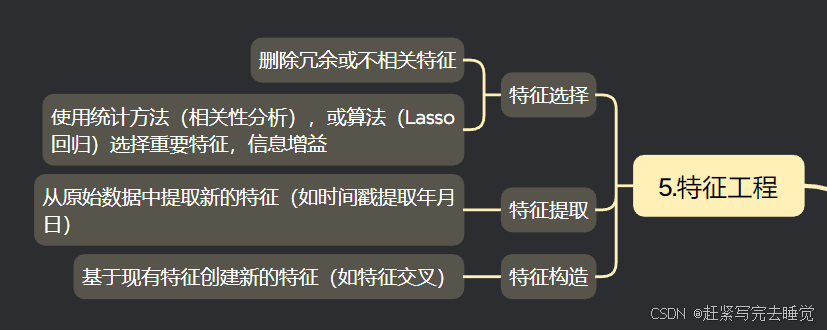
特征工程是指从原始数据中提取、构建和选择对模型有意义的特征的过程,旨在通过一系列操作提升数据特征的质量,特征工程包括数据预处理、特征选择、特征提取,特征构造等等,一般需要做的是数据预处理,像特征选择使用较少,如遇到了随时间变化的数据可以进行特征选择。(不是很常用),下面简单介绍:
特征选择:
删除冗余或不相关特征:在众多的原始特征中,有些特征可能是重复的或者与目标变量毫无关联,去除这些特征可以减少模型的复杂度,提高模型训练效率和准确性。通过使用统计方法(相关性分析)删除相关性较大的其他几项,或算法(Lasso 回归)可以将一些不重要的特征系数压缩为 0,从而实现特征选择。
终于把机器学习中的特征选择搞懂了!!
特征提取:
从原始数据中提取新的特征(如时间戳提取年月日):原始数据可能存在于复杂的形式中,通过提取其中有价值的信息形成新的特征。例如,将一个包含日期和时间的时间戳数据,提取出年、月、日、小时等信息,这些新的特征可能对某些模型更有帮助。
特种构造:
基于现有特征创建新的特征(如特征交叉):通过对现有的特征进行组合、运算等操作来创建新的特征。例如在电商数据中,将用户的购买频率和购买金额进行相乘,构造出一个新的特征来表示用户的消费力度,这可能会更好地反映用户的消费行为特征。
好了,本篇博客的数据预处理就介绍到这里,该专栏会持续更新数学建模的内容,需要的可以订阅收藏一下,如果本博客对您有所帮助,请留下您的赞赞哦!
有什么问题可以在评论区留言哦!感谢您的阅读!