数据结构-4.Java. 栈与队列
本篇博客给大家带来的是栈和队列的知识点, 其中包括两道面试OJ题 用队列实现栈 和 用栈实现队列.
文章专栏: Java-数据结构
若有问题 评论区见
欢迎大家点赞 评论 收藏 分享
如果你不知道分享给谁,那就分享给薯条, 如果分享不成功, 那我就会回你一下,那样你就分享成功啦.
你们的支持是我不断创作的动力 .
1.栈(Stack)
1.1概念
栈: 一种特殊的线性表, 只许在固定的一端进行插入和删除元素操作. 进行数据插入和删除操作的一端称为栈顶, 另一端称为栈底. 栈中的数据元素遵守后进先出的原则.
在栈顶入数据称为压栈, 在栈顶出数据称为出栈.
1.2栈的使用
public static void main(String[] args) { Stack stack = new Stack(); stack.push(12); stack.push(23); stack.push(34); System.out.println(stack.size());//获取栈中有效元素个数-->4 System.out.println(stack.peek());//获取栈顶元素-->4 Integer x = stack.pop();//获取并删除栈顶元素 System.out.println(x); System.out.println(stack.isEmpty());//判断栈是否为空. }1.3 栈的模拟实现
Stack继承了Vector, Vector 和 ArrayList 类似, 都是动态的顺序表, 不同的是Vector是线程安全的。
栈 是由 顺序表实现的,所以操作与顺序表大致相同.
public class MyStack { private int[] elem; private int usedSize; private static final int DEFAULT_CAPACITY = 10; public MyStack() { this.elem = new int[DEFAULT_CAPACITY]; } //新增元素 public void push(int val) { if(isFull()) { //空间不足,扩二倍. this.elem = Arrays.copyOf(this.elem, 2 * this.elem.length); } this.elem[usedSize] = val; usedSize++; } public boolean isFull() { return usedSize == elem.length; } public int pop() { if(isEmpty()) { System.out.println(\"栈为空\"); /*throw new EmptyException();*/ } int OldVal = elem[usedSize-1]; usedSize--; return OldVal; } public int peek() { if(isEmpty()) { System.out.println(\"栈为空\"); /*throw new EmptyException();*/ } return elem[usedSize-1]; } private boolean isEmpty() { return usedSize == 0; } }1.4栈的应用场景
1. 改变元素的序列
2. 将递归转化为循环
1.5概念区分
栈 , 虚拟机栈 , 栈帧有什么区别 ?
本章所学的栈为数据结构栈, 虚拟机栈是内存当中的一块区域.
每次调用方法都需要在栈上给方法开辟一块内存,这块内存就是栈帧.
2.队列(Queue)
2.1概念
队列: 只允许在一端进行插入数据操作, 在另一端进行删除数据操作的特殊线性表, 队列具有先进先出特性, 进行插入操作的一段称为队尾, 这一操作是入队列.进行删除操作的一端称为队头,这一操作称为出队列.
2.2队列的使用
在Java中,Queue是个接口, 底层是通过链表实现的.
public static void main(String[] args) { Queue queue = new LinkedList(); queue.offer(1); queue.offer(2); queue.offer(3);//从队尾入队列. System.out.println(queue.size());//队列长度 System.out.println(queue.poll());//删除并返回队头元素 System.out.println(queue.peek());//瞄一眼队头元素 if(queue.isEmpty()) { System.out.println(\"队列为空\"); }else { System.out.println(queue.size()); } }2.3队列模拟实现
public class MyLinkedListQueue { class ListNode { ListNode prev; ListNode next; int val; public ListNode(int val) { this.val = val; } } ListNode head; ListNode last; private int usedSize = 0; //插入元素 public void offer(int val) { ListNode node = new ListNode(val); if(isEtmpty()) { head = last = node; usedSize++; }else { last.next = node; node.prev = last; last = node; usedSize++; } } //删除队头节点并返回其元素值 public int poll() { if(isEtmpty()) { return -1; }else { //只有一个节点 if(head.next == null) { int ret1 = head.val; head = last = null; usedSize--; return ret1; } //两个节点及以上: int ret2 = head.val; head = head.next; head.prev = null; usedSize--; return ret2; } } //peek头节点的值 public int peek() { if(isEtmpty()) { return -1; }else { return head.val; } } //得到数据个数 public int getUsedSize() { return usedSize; } public boolean isEtmpty() { return usedSize == 0; }}2.4循环队列
实际中我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者消费者模型时可以就会使用循环队列。 环形队列通常使用数组实现。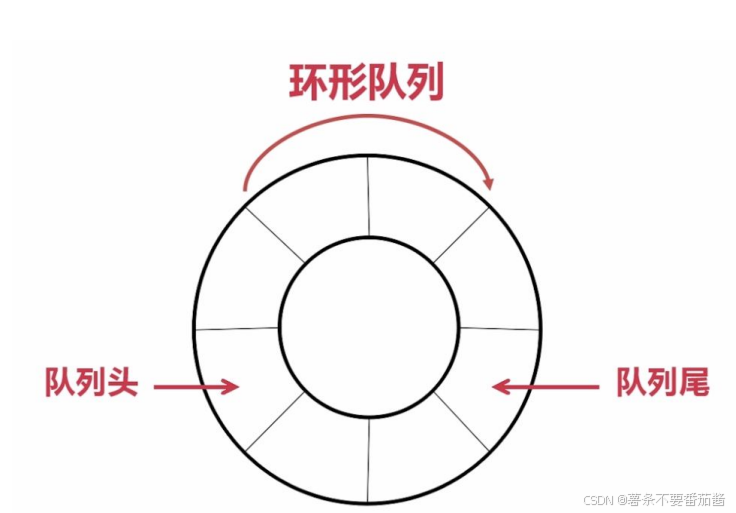 
先来看循环队列怎么插入元素 队头和队尾都处于0下标处, 那么rear = front时,队列为空. 从0下标处开始插入元素. 
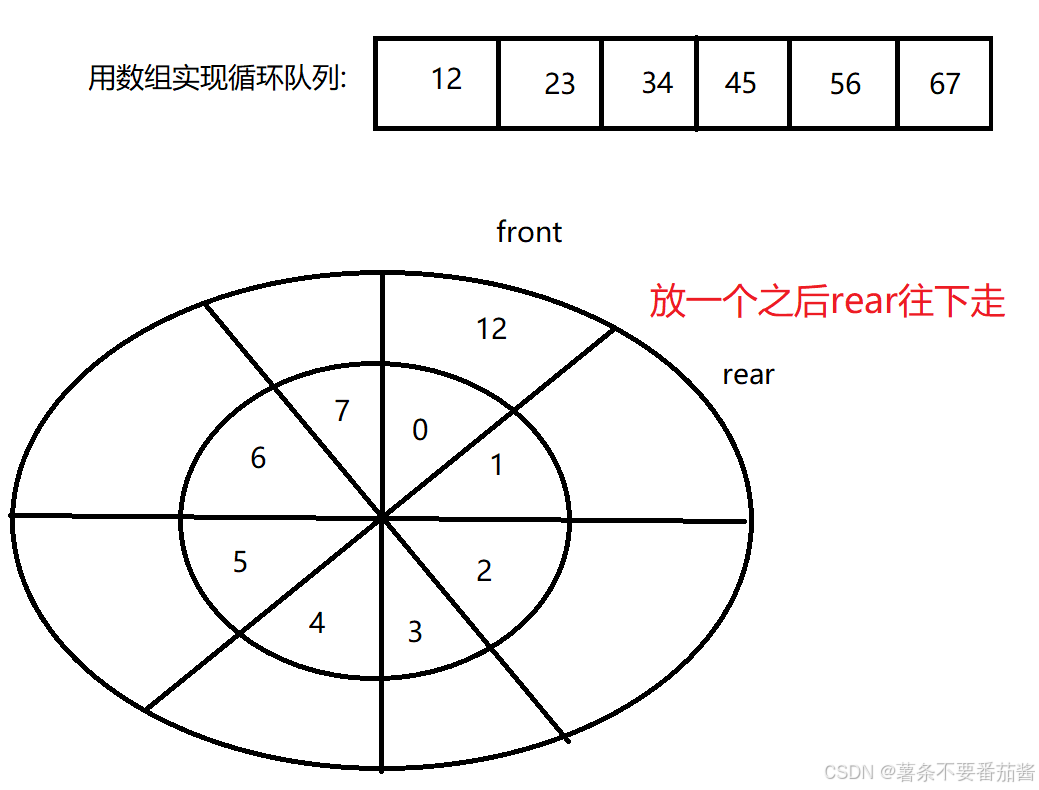当rear走到 7 下标时, rear 如果继续++, rear=8越界, 所以rear不能简单的++. 又想让rear回到0下标. 可以rear = (rear+1)%elem.length;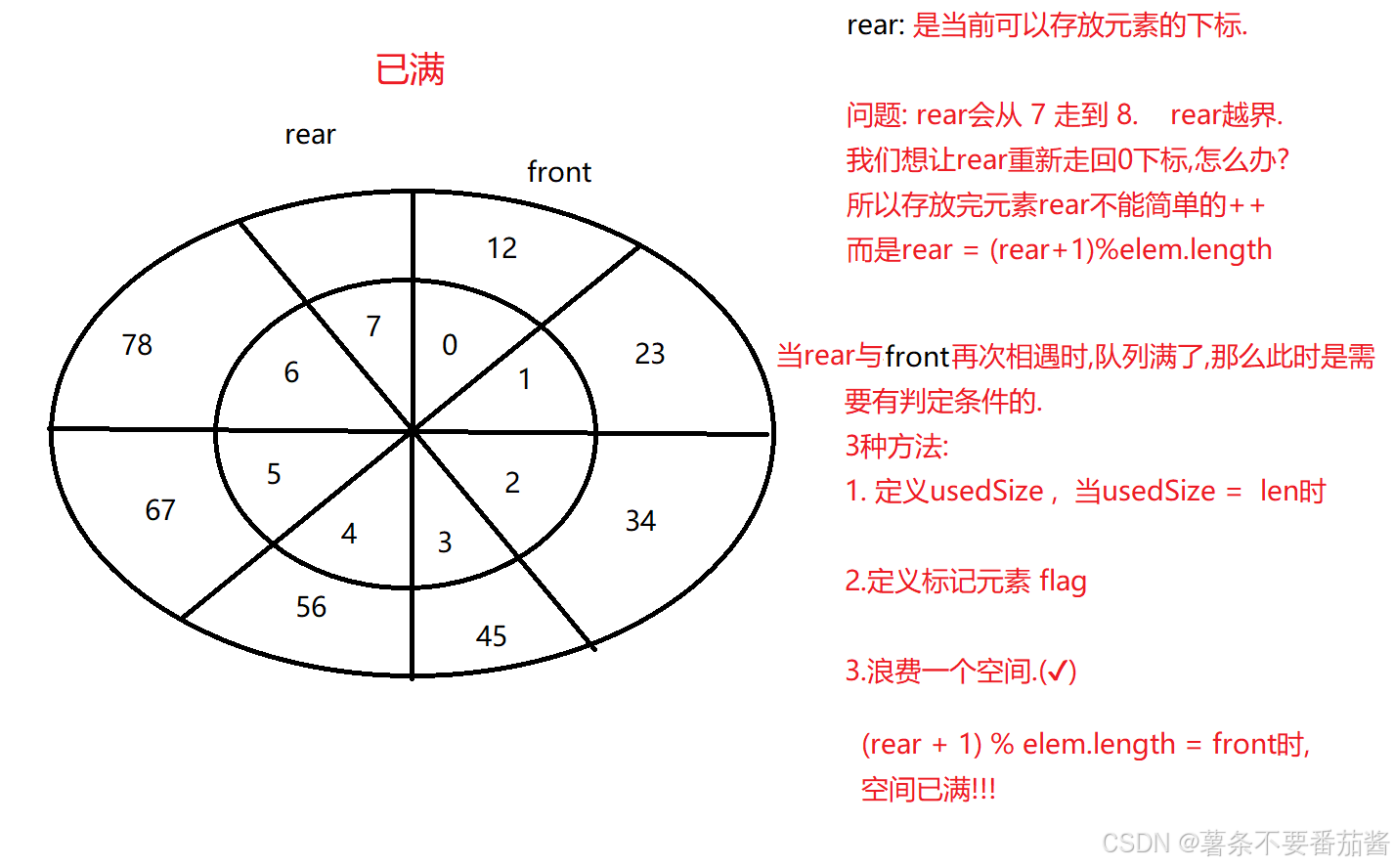 
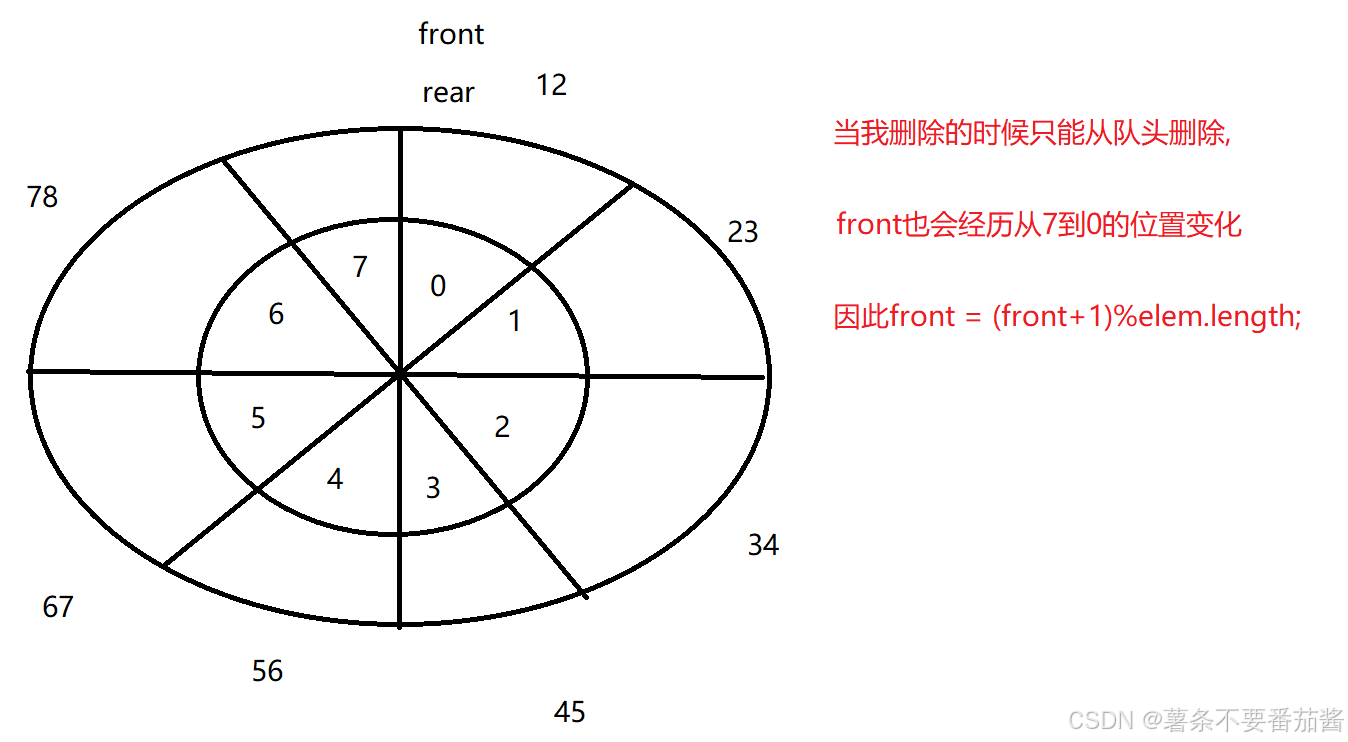622. 设计循环队列 - 力扣（LeetCode）按照上面的思路写一写这道OJ题, 答案如下:
class MyCircularQueue { private int[] elem; private int front; private int rear; public MyCircularQueue(int k) { this.elem = new int[k+1]; } public int Front() { if(!isEmpty()) { return elem[front]; } return -1; } public int Rear() { if(!isEmpty()) { int index = (rear == 0) ? elem.length - 1 : rear-1; return elem[index]; } return -1; } public boolean enQueue(int value) { if(isFull()) { return false; } elem[rear] = value; rear = (rear+1)%elem.length; return true; } public boolean deQueue() { if(isEmpty()) { return false; } front = (front+1)%elem.length; return true; } //检查队列是否为空 public boolean isEmpty() { return rear == front; } //检查队列是否已满 public boolean isFull() { return (rear+1)%elem.length == front; }}3.栈与队列互相实现的OJ题
225. 用队列实现栈 - 力扣（LeetCode）
1. 入栈怎么入呢?定义两个队列qu1和qu2, 都为空默认入到qu1, 只有一个为空,就是哪个不为空入哪个, 都不为空入到qu1.
public void push(int x) { if(!qu1.isEmpty()) { qu1.offer(x); }else if(!qu2.isEmpty()) { qu2.offer(x); }else { qu1.offer(x); } }2. 出栈怎么出呢?画图分析,不难得出实现栈至少需要两个队列.
两个队列怎么做到先出45呢?
执行上图操作后, 再出qu1队头元素,就做到了先出45.
接着 如果要删除34也是一样的, 先把12和23在 qu2出队 到 qu1...
public int top() { if(empty()) { return -1; } if(!qu1.isEmpty()) { int tmp = 0; int size = qu1.size(); for (int i = 0; i < size; i++) { tmp = qu1.poll(); qu2.offer(tmp); } return tmp; }else { int size = qu2.size(); int tmp1 = 0; for (int i = 0; i < size; i++) { tmp1 = qu2.poll(); qu1.offer(tmp1); } return tmp1; } } public boolean empty() { return qu1.isEmpty() && qu2.isEmpty(); }}整道题的答案
class MyStack { private Queue qu1; private Queue qu2; public MyStack() { qu1 = new LinkedList(); qu2 = new LinkedList(); } public void push(int x) { if(!qu1.isEmpty()) { qu1.offer(x); }else if(!qu2.isEmpty()) { qu2.offer(x); }else { qu1.offer(x); } } public int pop() { if(empty()) { return -1; } if(!qu1.isEmpty()) { int size = qu1.size(); for (int i = 0; i < size-1; i++) { int tmp = qu1.poll(); qu2.offer(tmp); } return qu1.poll(); }else { int size = qu2.size(); for (int i = 0; i < size-1; i++) { int tmp = qu2.poll(); qu1.offer(tmp); } return qu2.poll(); } } public int top() { if(empty()) { return -1; } if(!qu1.isEmpty()) { int tmp = 0; int size = qu1.size(); for (int i = 0; i < size; i++) { tmp = qu1.poll(); qu2.offer(tmp); } return tmp; }else { int size = qu2.size(); int tmp1 = 0; for (int i = 0; i < size; i++) { tmp1 = qu2.poll(); qu1.offer(tmp1); } return tmp1; } } public boolean empty() { return qu1.isEmpty() && qu2.isEmpty(); }}232. 用栈实现队列 - 力扣（LeetCode）
1. 入队, 将所有元素入到第一个栈中 s1.
2.出队, 把第一个栈中所有元素全部倒回第二个栈中, 出s2 的栈顶元素即可.
class MyQueue { Stack s1; Stack s2; public MyQueue() { s1 = new Stack(); s2 = new Stack(); } public void push(int x) { s1.push(x); } public int pop() { if(empty()) { return -1; } if(s2.empty()) { while(!s1.empty()) { s2.push(s1.pop()); } } return s2.pop(); } public int peek() { if(empty()) { return -1; } if(s2.empty()) { while(!s1.empty()) { s2.push(s1.pop()); } } return s2.peek(); } public boolean empty() { return s1.size() == 0 && s2.size() == 0; }}以上就是本文的全部内容了, 感谢观看!!!
