网站导航
> 技术文档 > 【c++】STL容器-位图、位图关于海量数据处理的应用

【c++】STL容器-位图、位图关于海量数据处理的应用

网友: 技术文档 2025-08-08 00:43:47

小编个人主页详情<—请点击
小编个人gitee代码仓库<—请点击
c++系列专栏<—请点击
倘若命中无此运，孤身亦可登昆仑，送给屏幕面前的读者朋友们和小编自己!
在这里插入图片描述

目录

    • 前言
    • 一、概念引入
    • 二、位图概念介绍
    • 三、位图的模拟实现
      • 铺垫
      • set
      • reset
      • test
        • 测试
    • 四、海量数据处理
      • 题目一
        • twobitset
          • 模拟测试
      • 题目二
          • 模拟测试
      • 题目三
        • twoset1
          • 模拟测试
    • 五、源代码
      • BitSet.h
      • test.cpp
    • 总结

前言

【c++】STL容器-unordered_map/unordered_set的封装（逐步完善讲解）——书接上文 详情请点击<——
本文由小编为大家介绍——STL容器-位图

位图的set和reset和test跟位运算有关，关于位运算的讲解，小编已经准备好了【位运算】位运算框架笔记 详情请点击<——

一、概念引入

在进行正式讲解位图前，小编先用一道腾讯面试题来引入位图
腾讯面试题：给40亿个不重复的无符号整数，没排过序。给定一个无符号整数，如何快速判断给定的一个无符号整数是否存在40亿个无符号整数中？（有可能进行查询多次无符号整数）

  1. 方法一：遍历，时间复杂度O(N)，如果多次查询，需要多次遍历40亿个无符号整数，消耗大
  2. 方法二：先进行排序O(N * logN)，再使用二分O(logN)进行查找，40亿个无符号整数，在32位环境下，一个无符号整数的大小是4字节（64位环境下，一个无符号整数的大小是8字节），那么我们进行推算一下1G大约等于多少字节

1G == 1024MB (2^10KB) == 1024 * 1024KB (2^20KB) == 1024 * 1024 * 1024Byte(2^30Byte)
那么也就是1G大约是10亿字节(Byte)

  1. 回归方法二，那么40亿个无符号整数，一个整数是四个字节，那么40亿个无符号整数就是160亿个字节(Byte)，由于1G == 10亿字节，所以40亿个无符号整数约等于16G，要进行排序需要在内存才能进行排序，内存的空间一般不足以满足这里的16G的需求进行排序，所以方法二也不行
  2. 方法三：哈希，同样的哈希也需要内存，同样的内存没有那么大的空间，不满足，所以方法三不行
  3. 方法四：位图，给定的无符号整数是否在40亿个无符号整数内，进行判断无符号整数是在或者不在，刚好是两种状态，那么我们就可以使用二进制比特位0， 1来表示这两种状态，如果比特位是1，那么表示存在，如果比特位是0，那么表示不存在，将这40亿个不重复的无符号整数放到位图中表示状态之后，进行查询给出的无符号数就可以使用O(1)的时间复杂度快速的查询判断是否存在

二、位图概念介绍

位图：位图就是用每一位来存放某种状态，适用于海量数据，无重复数据的应用场景。通常用于判断数据在不在的场景

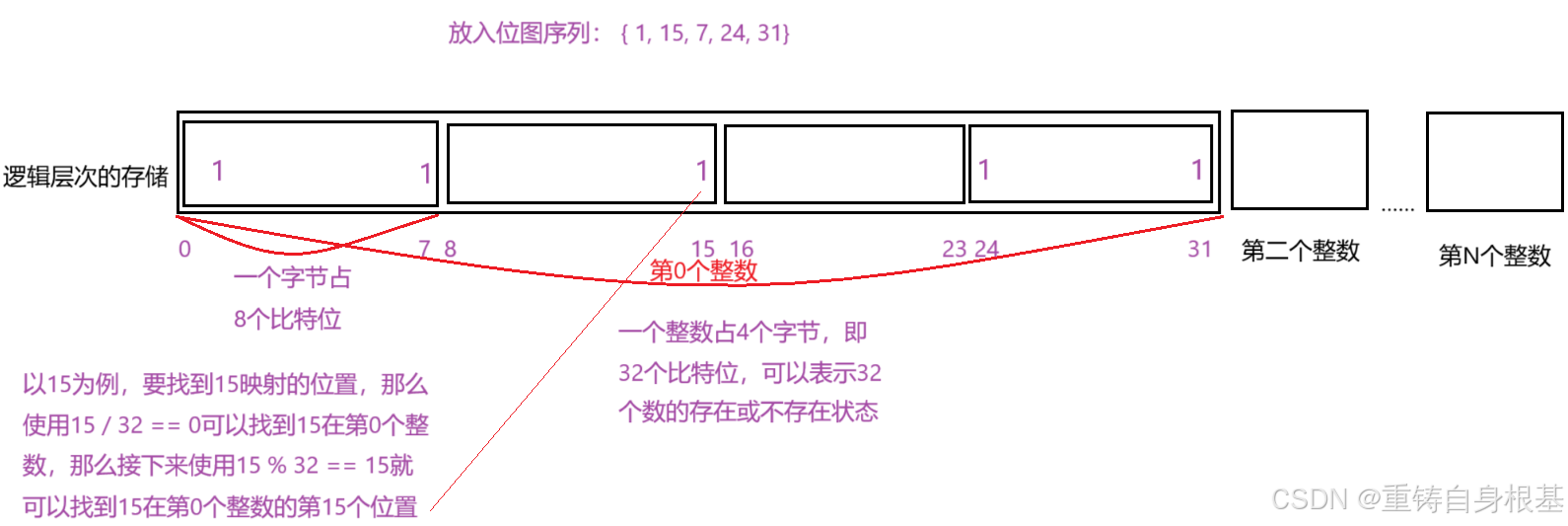
【c++】STL容器-位图、位图关于海量数据处理的应用

  1. 为了便于读者友友理解，上图小编是以逻辑的存储模式为例进行讲解的，我们只需要关心位图的逻辑层次的存储即可，不需要关心存储的底层究竟是使用大端机器存放还是使用小端机器存放，以VS为例，它的底层就是小端机器存储，验证如下
#include using namespace std;int main(){int a = 1;return 0;}
  1. 调出内存窗口，输入&a，输入后按下回车，同时列选择4，即可显示出变量a在内存中的实际存储，如下图，对于整数a来讲它的逻辑层面底层存储是0000 0000 0000 0000 0000 0000 0000 0001，那么换算成16进制是（数据的高位） 0001（数据的低位），小端机器是将数据的低位放到低地址处，对于那么就是反着地址进行存储，虽然符合人从低位到高位读取，但是由于是按照字节序进行存储，每个字节序的内部顺序保持不改变，所以进行讲解的时候不好理解
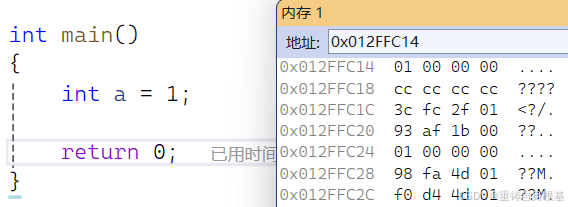
    【c++】STL容器-位图、位图关于海量数据处理的应用
  2. 同样的大端机器则是将数据的低位放到高地址处，我们需要从后向前进行讲解，进行讲解同样不方便，所以小编采用逻辑层次的存储进行讲解
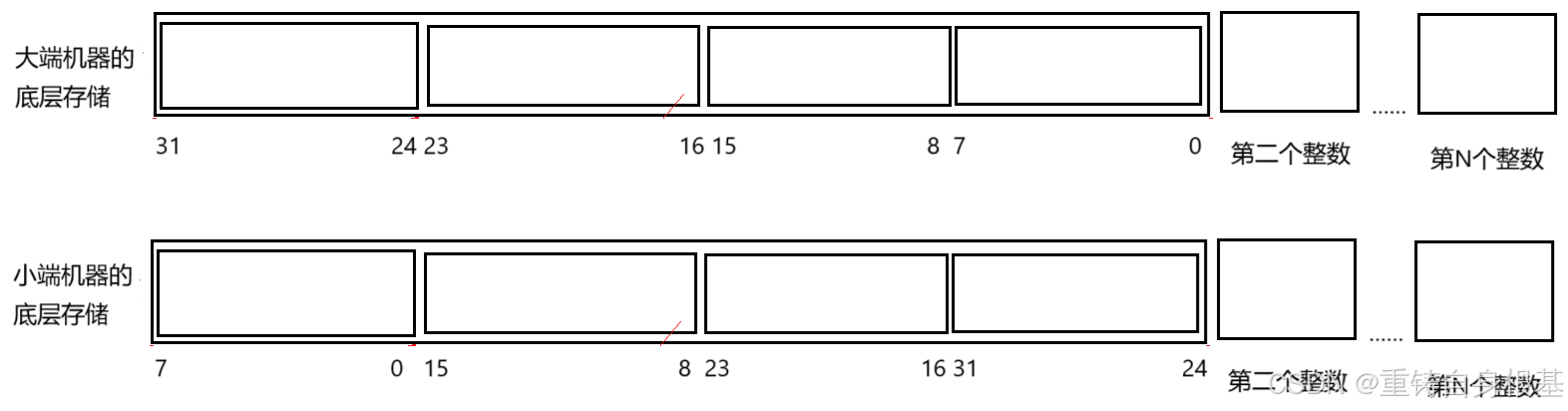
    【c++】STL容器-位图、位图关于海量数据处理的应用
  3. 在编写位图中我们需要进行一系列的位运算，将对应存储位置上的比特位变成我们指定的0或1，或者判断指定位置上是否为1或0即可，不需要关心底层如何进行操作
  4. 同时这里使用位图去统计40亿个不重复的无符号整数，由于是要统计无符号整数，那么无符号整数就有可能会出现在无符号整数范围内的任意一个位置，出现任意一个大小的无符号整数，所以实际开的范围是无符号的范围，无符号数的范围是42亿9千万，无符号数在32位下的大小是4个自己，那么42亿9千万个无符号数，当我们使用位图去开空间的时候，就要开42亿9千万个比特位，那么就是42亿9千万比特位就是大约5亿字节，1G大约是10亿字节，那么也就是大约0.5G，也就是500MB，可见使用位图还是很节省空间的，并且内存开500MB的空间也完全可以开出来
  5. 那么如何对位图开42亿9千万比特位的空间呢，如下
int main(){wzx::bitset<-1> bs1;wzx::bitset<UINT32_MAX> bs2;return 0;}

三、位图的模拟实现

铺垫

  1. 由于在c++的STL库中也有位图，所以我们的位图命名上会和STL库冲突，那么我们将我们实现的位图放在我们自己的命名空间中
  2. 位图是对比特位进行操作，但是我们的存储类型是char，int，最小单位是char一个字节，其次是int四个字节，这里小编采用int进行存储，感兴趣的读者友友也可采用char来实现位图
  3. 那么我们就可以给位图定义一个私有成员变量_a类型是vector，用于对我们的位图进行管理与控制
  4. 位图不可以扩容，在最初的时候我们就要传入位图控制比特位的个数，使用size_t类型的参数初始化位图，那么位图的模板参数就为非类型模板参数N
  5. 位图的构造函数，那么我们利用非类型模板参数N（N表示位图中要表示多少数量的比特位）计算一共需要开多少个整型int即可，计算则采用N / 32，因为一个int可以表示32个比特位，由于是采用的 / 进行的计算，拿40进行举例，在计算机中40 / 32 == 1，有余数8被忽略了，即没有办法表示全40个比特位，所以我们应该在计算结果中加1，多开一个整型int，用于预防 / 运算后有余数， 表示全比特位
#pragma once#include using namespace std;namespace wzx{template<size_t N>class bitset{public:bitset(){_a.resize(N / 32 + 1);}private:vector<int> _a;};}
  1. 继续向下学习需要先掌握位运算，基础位运算的计算如下
    【c++】STL容器-位图、位图关于海量数据处理的应用

set

  1. set是将x位置上的比特位设置成1
    【c++】STL容器-位图、位图关于海量数据处理的应用
void set(size_t x){size_t i = x / 32;//i表示在第几个整数上size_t j = x % 32;//j表示在i的第几位上_a[i] |= (1 << j);}

reset

  1. reset是将x位置上的比特位设置成0
    【c++】STL容器-位图、位图关于海量数据处理的应用
void reset(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] &= (~(1 << j));}

test

  1. 判断指定位置x上是否为1或0即可
    【c++】STL容器-位图、位图关于海量数据处理的应用
bool test(size_t x){size_t i = x / 32;size_t j = x % 32;return (_a[i] >> j) & 1;}
测试
  1. 使用如下代码测试位图的三个接口
#include using namespace std;#include \"BitSet.h\"int main(){wzx::bitset<100> bs;bs.set(1);bs.set(10);bs.set(100);cout << bs.test(1) << endl;cout << bs.test(10) << endl;cout << bs.test(100) << endl << endl;bs.reset(10);cout << bs.test(1) << endl;cout << bs.test(10) << endl;cout << bs.test(100) << endl << endl;return 0;}

运行结果如下，正确
【c++】STL容器-位图、位图关于海量数据处理的应用

四、海量数据处理

下面小编将使用三道题目讲解位图在海量数据处理的应用

题目一

给定100亿个整数，设计算法找出只出现一次的整数

  1. 由于题目的需求是找到只出现一次的整数，那么我们就需要进行统计整数的次数，这些整数有出现0次的，有只出现一次的，有出现两次及以上的整数，那么我们并不需要真的统计出所有整数出现的次数，而是使用出现0次，出现1次，出现2次进行统计，其中出现2次代表出现了两次及以上的次数
  2. 我们可以巧妙的使用位图的两个比特位去控制，因为两个比特位可以表示00，01，10，11，对应到二进制位其中00表示出现0次，01表示出现1次，10表示出现了两次（这道题目中特殊应用，使用10表示出现了两次及以上，即当一个数字已经出现了两次之后，再出现一次我们仍然使用两次进行统计，因为这里的两次表示出现了两次即以上），11在这道题目中不需要进行设置，因为00，01，10已经可以满足我们的需求了
  3. 我们可以在一个位图中去控制两个比特位进行控制表示，但是通常使用一个位图去控制两个比特位比较难以控制，我们退而求其次使用使用STL库中的位图进行封装去封装一个类twobitset两个位图进行控制，第一个位图控制第一位，第二个位图控制第二位，例如想要在第4位上设置01，那么就在第一个位图的第四位上设置0，第二个位图上设置1
  4. 同时我们设置两个图的test，这个test特定的判断x所处的位是否是只出现一次的，那么就是01，即第一个位图的x位上是0，第二个位图的x位上是1才返回真，否则返回假的
  5. 使用两个图统计100亿个整数，统计完成后，再遍历整数，调用两个位图的test即可找出只出现一次的整数
  6. 为了实现出两个位图，那么我们可以对使用STL库中的位图进行封装进行封装实现出一个类twobitset
twobitset
  1. 两个位图由于要封装位图，位图需要非模板参数实例化，所以两个位图也需要非类型模板参数N
  2. 两个位图的set的作用就是统计次数，当x位上的数是0的时候，那么就是将0进行加加变成1，那么就是将第一个位图设置成0，第二个位图设置成1，当x位上的数是1的时候，那么就是将1进行加加变成2，那么就是将第一个位图设置成1，第二个位图设置成0，当x再次出现在两个位图的set的时候就不进行处理了，因为两个位图的set其中表示的x位是2，就已经表示了x已经出现了两次及以上了，我们的需求是统计只出现一次的数，并不是要将所有的数的出现次数全部统计出来
  3. 两个位图的test的作用是判断这个x位上的数是否是出现一次的数，也就是第一个位图x位上是0，第二个位图上x位上是1，那么合起来二进制位01，那么换算成10进制，就是1，也就是只出现了一次，此时我们返回真，否则返回假
#include #include  using namespace std;template<size_t N>class twobitset{public:void set(size_t x){if (!bs1.test(x) && !bs2.test(x)){bs2.set(x);}else if (!bs1.test(x) && bs2.test(x)){bs1.set(x);bs2.reset(x);}}bool test(size_t x){return !bs1.test(x) && bs2.test(x);}private:bitset<N> bs1;bitset<N> bs2;};
模拟测试
  1. 使用10以内的整数进行模拟测试
  2. 如果实际中对应到上面题目，那么数据就是10亿个整数，整数的范围是-2147483648 ~ 2147483647，同样的由于整数有正负，从负的21亿7千万，到正的21亿7千万，所以我们需要开的范围大小是42亿9千万，整数0映射到21亿7千万开始进行统计，也就是将数加上21亿7千万才放入位图中进行统计，这样处理是为了应对负数的情况，位图中不可以表示负数的状态，所以采用加上21亿7千万进行间接映射到位图中统计状态，同时使用for循环进行遍历的找出现一次的时候，数据范围也是-2147483648 ~ 2147483647，对应到两个位图中的test的时候要加上21亿7千万才行，如果test返回为真，那么i此时的数就是只出现一次的数，循环统计所有的即可
int main(){int a[] = { 1, 1, 5, 1, 2, 6, 2, 6, 9 };wzx::twobitset<10> bs;for (auto e : a){bs.set(e);}for (size_t i = 0; i < 10; i++){if (bs.test(i)){cout << i << \' \';}}cout << endl;return 0;}

运行结果如下，正确
【c++】STL容器-位图、位图关于海量数据处理的应用

题目二

题目：给两个文件，分别有100亿个整数，我们只有1G内存，如何找到文件的交集？

  1. 同样的对于整数，我们使用位图进行统计即可，首先需要明确一点，文件的交集，不包含多个重复的整数，比如文件一有三个2，文件二有两个2，那么文件一和文件二的交集就是2，这个2是一个2，所以我们可以使用位图去统计，并且使用位图一去统计文件一，使用位图二去统计文件二，这里位图需要开多少空间，读者友友可以先思考一下？
  2. 记住，位图永远是开范围，位图统计的是整数，那么就要开整数的范围，由于整数中也有负数，所以需要类似于题目一去开42亿9千万个比特位，并且42亿9千万个比特位等于5亿个字节，1G大约是10亿字节，所以一个位图开的空间是5亿个字节，也就是0.5G，由于我们需要使用两个位图，所以两个位图占用1G，正好符合题目要求
  3. 那么接下来使用位图一去统计文件一，使用位图二去统计文件二，进行统计的时候，由于整数有负数，需要进行间接映射，那么就是需要加上21亿7千万进行set统计，使用for循环，for循环的范围是整数范围，类似于题目一的做法，从负21亿7千万开始进行循环，使用位图一和位图二进行test的时候要加上21亿9千万，并且要位图一和位图二对应位置上同时满足真才是两个文件的交集之一
模拟测试
  1. 使用两个数组模拟两个文件进行测试
int main(){int a1[] = { 1, 1, 5, 7, 2, 6, 2, 6, 9 };int a2[] = { 1, 2, 7, 7, 8 };wzx::bitset<10> bs1, bs2;for (auto e : a1){bs1.set(e);}for (auto e : a2){bs2.set(e);}for (size_t i = 0; i < 10; i++){if (bs1.test(i) && bs2.test(i)){cout << i << \' \';}}cout << endl;return 0;}

运行结果如下，正确
【c++】STL容器-位图、位图关于海量数据处理的应用

题目三

一个文件有100亿个整数int，我们只有1G内存，如何设计算法找出出现次数不超过两次的所有整数

twoset1
  1. 思考一下，这里是不是很类似题目一，找出出现次数为1次的整数，类似的要使用类似于题目一的思路进行求解，只不过这里需要将11也用上，表示出现三次及以上的整数，同时对twoset的set进行修改，当x出现次数是2次的时候，x再次出现，将位图一的x位上设置成1，将位图二的x位上设置成1，表示11，出现了三次，当x已经出现了三次之后，x再次出现，此时由于位图一和位图二上的3表示x出现了三次及以上，所以进行处理
  2. 对于twoset的test进行修改，返回当x1出现0并且x2出现1，或者当x1出现1并且x2出现0返回真即可，否则返回假
  3. 为了和题目一的twoset进行区分，这里我们实现的类设置成twoset1
template<size_t N>class twobitset1{public:void set(size_t x){if (!bs1.test(x) && !bs2.test(x)){bs2.set(x);}else if (!bs1.test(x) && bs2.test(x)){bs1.set(x);bs2.reset(x);}else if (bs1.test(x) && !bs2.test(x)){bs1.set(x);bs2.set(x);}}bool test(size_t x){return !bs1.test(x) && bs2.test(x) || bs1.test(x) && !bs2.test(x);}private:bitset<N> bs1;bitset<N> bs2;};
模拟测试
  1. 使用如下代码进行模拟测试
  2. 如果是真实情景，那么就要使用和题目一中小编将的相对映射处理整数的负数
int main(){int a[] = { 1, 1, 5, 1, 1, 2, 2, 3, 3, 3 };wzx::twobitset1<10> bs;for (auto e : a){bs.set(e);}for (size_t i = 0; i < 10; i++){if (bs.test(i)){cout << i << \' \';}}cout << endl;return 0;}

运行结果如下，正确
【c++】STL容器-位图、位图关于海量数据处理的应用

五、源代码

BitSet.h

#pragma once#include using namespace std;namespace wzx{template<size_t N>class bitset{public:bitset(){_a.resize(N / 32 + 1);}void set(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] |= (1 << j);}void reset(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] &= (~(1 << j));}bool test(size_t x){size_t i = x / 32;size_t j = x % 32;return (_a[i] >> j) & 1;}private:vector<int> _a;};template<size_t N>class twobitset{public:void set(size_t x){if (!bs1.test(x) && !bs2.test(x)){bs2.set(x);}else if (!bs1.test(x) && bs2.test(x)){bs1.set(x);bs2.reset(x);}}bool test(size_t x){return !bs1.test(x) && bs2.test(x);}private:bitset<N> bs1;bitset<N> bs2;};template<size_t N>class twobitset1{public:void set(size_t x){if (!bs1.test(x) && !bs2.test(x)){bs2.set(x);}else if (!bs1.test(x) && bs2.test(x)){bs1.set(x);bs2.reset(x);}else if (bs1.test(x) && !bs2.test(x)){bs1.set(x);bs2.set(x);}}bool test(size_t x){return !bs1.test(x) && bs2.test(x) || bs1.test(x) && !bs2.test(x);}private:bitset<N> bs1;bitset<N> bs2;};}

test.cpp

#include using namespace std;#include \"BitSet.h\"//int main()//{//wzx::bitset bs;////bs.set(1);//bs.set(10);//bs.set(100);//////cout << bs.test(1) << endl;//cout << bs.test(10) << endl;//cout << bs.test(100) << endl << endl;////bs.reset(10);////cout << bs.test(1) << endl;//cout << bs.test(10) << endl;//cout << bs.test(100) << endl << endl;////return 0;//}//int main()//{//wzx::bitset bs1;//wzx::bitset bs2;////return 0;//}////int main()//{//int a[] = { 1, 1, 5, 1, 2, 6, 2, 6, 9 };//wzx::twobitset bs;////for (auto e : a)//{//bs.set(e);//}////for (size_t i = 0; i < 10; i++)//{//if (bs.test(i))//{//cout << i << \' \';//}//}//cout << endl;////return 0;//}//int main()//{//int a1[] = { 1, 1, 5, 7, 2, 6, 2, 6, 9 };//int a2[] = { 1, 2, 7, 7, 8 };//wzx::bitset bs1, bs2;////for (auto e : a1)//{//bs1.set(e);//}////for (auto e : a2)//{//bs2.set(e);//}////for (size_t i = 0; i < 10; i++)//{//if (bs1.test(i) && bs2.test(i))//{//cout << i << \' \';//}//}//cout << endl;//return 0;//}int main(){int a[] = { 1, 1, 5, 1, 1, 2, 2, 3, 3, 3 };wzx::twobitset1<10> bs;for (auto e : a){bs.set(e);}for (size_t i = 0; i < 10; i++){if (bs.test(i)){cout << i << \' \';}}cout << endl;return 0;}

总结

以上就是今天的博客内容啦,希望对读者朋友们有帮助
水滴石穿，坚持就是胜利，读者朋友们可以点个关注
点赞收藏加关注，找到小编不迷路！

网络标签：

相关问题