《Gaussian Shading: Provable Performance-Lossless Image Watermarking for Diffusion Models》 CVPR 2024

技术文档

论文：Gaussian Shading: Provable Performance-Lossless Image Watermarking for Diffusion Models

代码：Gaussian-Shading:[CVPR 2024] Gaussian Shading: Provable Performance-Lossless Image Watermarking for Diffusion Models - GitCode

一、研究背景与问题提出

1.1 扩散模型的发展与挑战

1.2 现有水印方法的缺陷

1.3 本文提出的方法

二、研究方法（重点）编辑

2.1 水印扩散

2.2 随机化

2.3 分布保持采样

2.4 后续图像生成

2.5 水印提取

2.6 无损性能证明——反证法

三、结果与分析

四、优点与创新

五、缺陷

这篇论文提出了一种针对扩散模型的图像水印技术Gaussian Shading，其核心优势是在不影响模型生成性能的前提下实现版权保护与内容溯源，并且做到了不需要进行额外的训练。

一、研究背景与问题提出

1.1 扩散模型的发展与挑战

扩散模型（如 Stable Diffusion）在图像生成领域表现卓越，但也引发了知识产权盗用、虚假内容生成等伦理问题。该研究挑战在于，现有方法通常会在嵌入水印后降低模型性能或需要额外训练，这不符合运营商和用户的期望——如何在嵌入水印的同时保持模型的生成质量和性能。

1.2 现有水印方法的缺陷

后处理方法（如 DwtDct、DwtDctSvd、RivaGAN ）：直接修改图像，降低画质。
微调方法（如 Stable Signature、DiffusionShield）：修改模型参数，增加计算开销。
潜在表示方法（如 Tree-Ring）：限制采样随机性，影响生成性能。

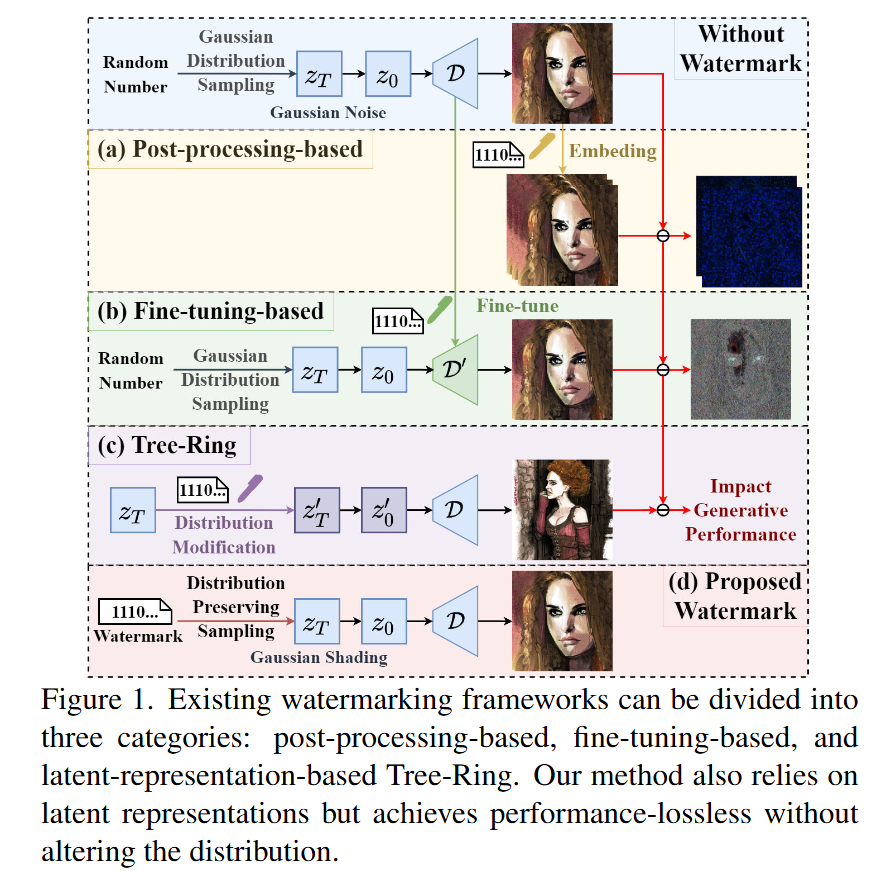
后处理方法牺牲图像质量，微调方法增加计算成本，潜在表示方法损害生成性能，体现了 “性能 - 鲁棒性 - 效率” 的三角矛盾。

1.3 本文提出的方法

因此本文提出了高斯阴影（Gaussian Shading），这是一种扩散模型水印技术，将水印映射到潜在空间中。兼具性能无损和无需训练的特点，同时实现版权保护和违规内容溯源的双重目的。此外，该水印嵌入无需修改模型参数，因此具有即插即用的特性。

潜在表示的关键特性包括：

语义保留：虽为低维张量，但包含图像生成所需的完整语义信息。

分布一致性：未加水印的潜在表示服从标准高斯分布，而 Gaussian Shading 通过特殊设计使加水印的潜在表示与原始分布一致，确保生成性能无损。——怎么理解？（在扩散模型中，潜在表示分布一致和模型一致能够保证生成图像一致，原因在于：潜在表示是图像的关键中间表示，承载着生成图像的核心语义信息，其分布一致意味着生成图像的基础信息相似；而模型决定了从潜在表示生成图像的过程，模型一致则保证了生成过程的稳定性和一致性。）

二、研究方法（重点）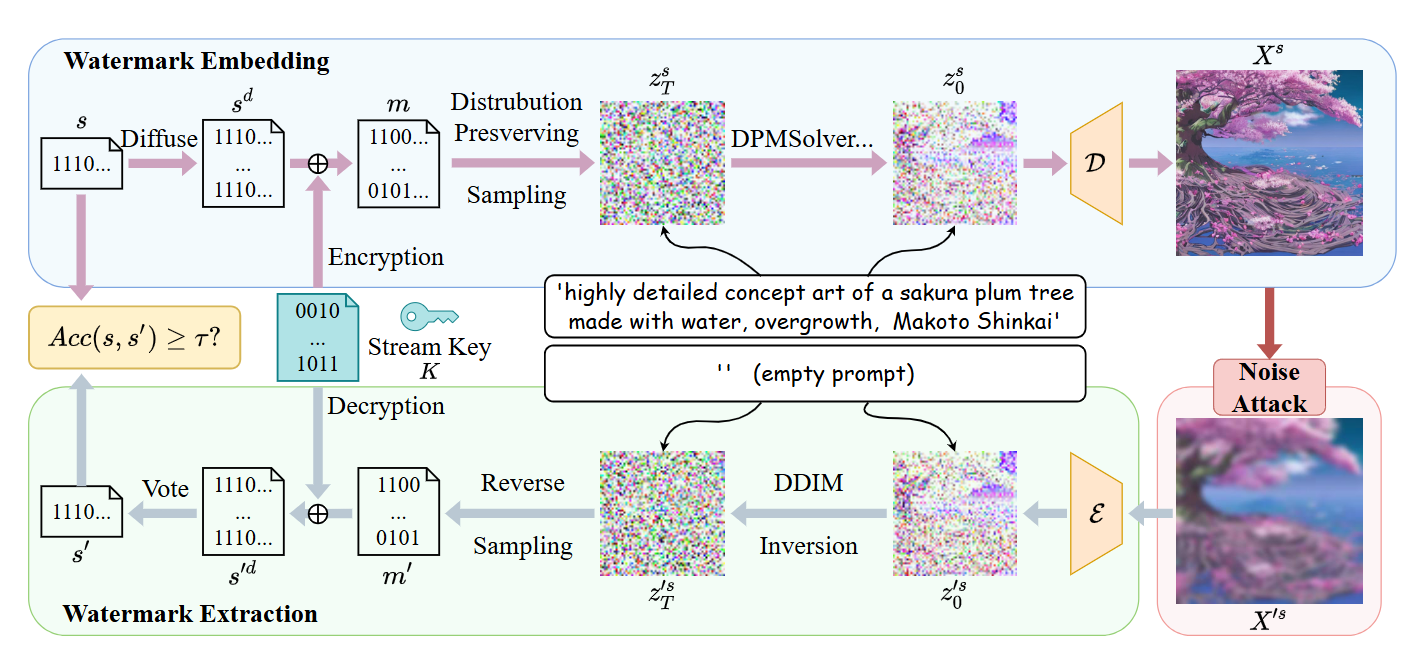

2.1 水印扩散

将水印信息压缩、复制并散布到潜在表示的所有维度中（包括通道、高度、宽度），使水印与图像的整体语义深度融合。

设潜在空间中每个维度可携带 $l$ 比特的水印信息，则理论水印容量为 $l \\times c \\times h \\times w$ 比特，即潜在空间的每个维度均为水印嵌入的载体。但现在为了增强水印对攻击的抵抗能力（如裁剪、压缩），设计了维度压缩与复制机制：

用扩散因子 $f_c$ 和 $f_{hw}$ 进行维度压缩：则原始水印 $s$ 尺寸为 $l \\times \\frac{c}{f_c} \\times \\frac{h}{f_{hw}} \\times \\frac{w}{f_{hw}}$ （这个是实际水印容量）

复制：确保扩展后的水印体积与原始潜在表示维度一致，原始水印复制扩展为 $s^d$ ，其维度为 $l \\times c \\times h \\times w$ ，与潜在表示维度完全匹配。

意义：水印信息通过扩散遍布整个潜在空间，与图像的全部语义特征（如物体轮廓、纹理、颜色分布）绑定，而不再局限于潜在空间的局部区域，避免因局部修改导致水印丢失。

2.2 随机化

实际场景中水印分布固定化会导致一定的安全风险。——因此流密码（如 ChaCha20）、引入流密钥 K 对 $s^d$ 进行逐位加密，将其转换为分布已知的随机化水印 m（m是一个随机二进制比特流）。

随机化水印的技术优势：

①安全性能提升，因为均匀分布的m没有明显的统计特性，可抵抗频率分析、模式匹配等攻击；

②鲁棒性增强，随机化处理使水印信息与潜在空间的语义特征解耦，避免因局部修改导致水印整体失效；

③分布一致性保证，由于 m 是随机二进制流，其分布与扩散模型初始采样的高斯分布兼容性高——后续分布保持采样的实现就是基于这样一个特点。

$s^d\\rightarrow m\\rightarrow Z^T_S$

这边 $m\\rightarrow Z^T_S$ 就是分布保持采样，怎么实现呢？看第三步。

2.3 分布保持采样

当每个维度表示 $l$ 比特随机化水印 $m$ 时，这 $l$ 比特可视为整数 $y \\in [0, 2^l - 1]$ ，服从离散均匀分布，即 $p(y) = \\frac{1}{2^l}$ 。设 $f(x)$ 为高斯分布 $N(0, I)$ 的概率密度函数，ppf表示分位数函数。将 $f(x)$ 划分为 $2^l$ 个等累积概率区间。当 $y = i$ 时，含水印的潜在表示 $z_T^s$ 落入第 $i$ 个区间，即 $z_T^s$ 应服从条件分布：

<img alt=\"p(z_T^s | y = i) = \\begin{cases} 2^l \\cdot f(z_T^s) & ppf\\left(\\frac{i}{2^l}\\right)

推导：

等累计概率区间的划分：

通过分位数函数 ppf 将高斯分布划分为 $2^l$ 个区间，每个区间的累计概率为 $\\frac{1}{2^l}$ 。

对于第 i 个区间，其上下界为： $a = ppf\\left(\\frac{i}{2^l}\\right), \\quad b = ppf\\left(\\frac{i+1}{2^l}\\right)$
则，高斯分布在区间 $(a, b]$ 内的累计概率为： $\\int_a^b f(x) \\, dx = F(b) - F(a) = \\frac{i+1}{2^l} - \\frac{i}{2^l} = \\frac{1}{2^l}$ ，其中 $F(x)$ 为高斯分布的累计分布函数（CDF）

条件概率的归一化要求：

根据条件概率定义， $p(z_T^s | y=i)$ 需满足： $\\int_{-\\infty}^{+\\infty} p(z_T^s | y=i) \\, dz = 1$ ，即： $\\int_a^b p(z_T^s | y=i) \\, dz = 1$

概率密度的线性缩放：
设条件概率密度为 $k \\cdot f(z_T^s)$ （这个线性假设比较有意思，其实没有很懂），代入上式得： $k \\cdot \\int_a^b f(z_T^s) \\, dz = k \\cdot \\frac{1}{2^l} = 1 \\quad \\Rightarrow \\quad k = 2^l$
因此，条件概率密度为 $2^l \\cdot f(z_T^s)$

分布保持的数学本质：

边际分布的一致性
条件概率密度 $p(z_T^s | y=i)$ 与 y 的离散均匀分布结合后，其边际分布为： $p(z_T^s) = \\sum_{i=0}^{2^l-1} p(z_T^s | y=i) \\cdot p(y=i) = \\sum_{i=0}^{2^l-1} 2^l \\cdot f(z_T^s) \\cdot \\frac{1}{2^l} = f(z_T^s)$
即 $z_T^s$ 的整体分布仍为标准高斯分布，实现 “分布保持”。

条件累积分布函数（Conditional Cumulative Distribution Function, CDF）：

<img alt=\"F(z_T^s | y=i) = \\begin{cases} 0 & z_T^s ppf\\left(\\frac{i+1}{2^l}\\right) \\end{cases}\" class=\"mathcode\" src=\"https://latex.csdn.net/eq?F%28z_T%5Es%20%7C%20y%3Di%29%20%3D%20%5Cbegin%7Bcases%7D%200%20%26%20z_T%5Es%20%3C%20ppf%5Cleft%28%5Cfrac%7Bi%7D%7B2%5El%7D%5Cright%29%20%5C%5C%202%5El%20%5Ccdot%20cdf%28z_T%5Es%29%20-%20i%20%26%20ppf%5Cleft%28%5Cfrac%7Bi%7D%7B2%5El%7D%5Cright%29%20%5Cleq%20z_T%5Es%20%5Cleq%20ppf%5Cleft%28%5Cfrac%7Bi+1%7D%7B2%5El%7D%5Cright%29%20%5C%5C%201%20%26%20z_T%5Es%20%3E%20ppf%5Cleft%28%5Cfrac%7Bi+1%7D%7B2%5El%7D%5Cright%29%20%5Cend%7Bcases%7D\" />

$cdf(x)$ 为标准高斯分布 $N(0, I)$ 的累积分布函数。

条件概率密度 $p(z_T^s | y=i) = 2^l \\cdot f(z_T^s)$ （区间内）与条件累积分布函数的关系为： $F(z_T^s | y=i) = \\int_{-\\infty}^{z_T^s} p(x | y=i) \\, dx$ ，在区间 $[ppf(i/2^l), ppf((i+1)/2^l)]$ 内积分得： $\\int_{ppf(i/2^l)}^{z_T^s} 2^l \\cdot f(x) \\, dx = 2^l \\cdot \\left[cdf(z_T^s) - cdf\\left(ppf\\left(\\frac{i}{2^l}\\right)\\right)\\right] = 2^l \\cdot cdf(z_T^s) - i$
与中间段完全一致，验证了两者的数学一致性。

有了条件累积分布函数，我们就可以通过对 $F(z_{T}^{s} | y=i)$ 进行随机采样时，获得相应的 $z_{T}^{s}$ 。

采样： $u = F(z_{T}^{s} | y=i) \\sim U(0, 1)$
移项： $z_{T}^{s} = ppf\\left(\\frac{u + i}{2^{l}}\\right)$ ，（累积分布函数（cdf）与分位数函数（ppf）互为反函数）

检验过程提取水印使用如下式子即可： $i=\\left\\lfloor 2^{l} \\cdot c d f\\left(z_{T}^{s}\\right)\\right\\rfloor$

2.4 后续图像生成

在完成采样过程后，水印已嵌入潜在表示 $z_{T}^{s}$ 中，后续的生成流程与稳定扩散模型（SD）的常规生成过程并无差异。在获得去噪后的 $z_{0}^{s}$ 后，通过解码器D生成含水印图像 $X^{s}$ ，即 $X^{s}=D(z_{0}^{s})$ 。

2.5 水印提取

2.6 无损性能证明——反证法

假设：含水印图像 $X^s$ 和不含水印图像 $X$ 可以区分，等价于公式⑦ $\\left| \\Pr\\left[\\mathcal{A}\\left(X^{s}\\right)=1\\right] - \\Pr\\left[\\mathcal{A}(X)=1\\right] \\right| = \\delta \\quad$ 成立，等价于公式⑩ $\\begin{aligned} \\left| \\Pr\\left[ \\mathcal{A}_{\\mathcal{E}, Q, S}(m) = 1 \\mid m = E(K, s^d) \\right] - \\Pr\\left[ \\mathcal{A}_{\\mathcal{E}, Q, S}(r) = 1 \\right] \\right| = \\delta \\end{aligned}$ 成立，即m序列和r序列可区分。

矛盾：公式和chacha20的不可区分性矛盾。

结论：初始假设错误，即 $X^s$ 和 $X$ 在多项式时间内不可区分。

三、结果与分析

见论文

四、优点与创新

性能无损：Gaussian Shading方法在不修改模型参数的情况下实现了水印嵌入，保证了生成图像的性能不受影响。

无需额外训练：该方法不需要对现有模型进行额外训练，可以直接集成到生成过程中，作为即插即用的模块。

高容量水印：利用Stable Diffusion的潜在空间，Gaussian Shading可以实现高达256位的水印容量，超过了现有方法。

理论证明：提供了水印嵌入性能无损的理论证明，确保了方法的可靠性。

鲁棒性：水印信息与图像语义紧密相关，对损失处理和擦除攻击具有很好的鲁棒性。

多场景应用：适用于版权保护和追踪违规内容的多种场景，包括检测、可追溯性和版权认证等。

五、缺陷

由于依赖 DDIM 反演方法，应用场景受到限制，这要求使用基于常微分方程求解器（ODE solvers）的连续时间采样器；
其次，高斯阴影采用流密码技术，因此在部署平台上需妥善进行密钥使用与管理。