超高被引！ESWA一区算法——灰雁优化算法（GGO）
注：该算法已按照智能优化算法APP标准格式进行整改，可直接集成到APP中，方便大家与自己的算法进行对比。
灰雁优化算法（Greylag Goose Optimization，GGO）是一种受到灰雁群体迁徙行为启发的智能优化算法。灰雁以其出色的飞行能力著称，在季节性迁徙中，它们组成经典的“V”字队形协同飞行，借助气流减少空气阻力，从而使群体飞行距离提升约 70%。这一高效协作机制成为科研人员的灵感来源。GGO 算法巧妙模拟了灰雁在集群飞行中协同导航、位置更新与能量共享的机制，并将其转化为数学模型，形成了一种新型群体智能优化方法。在特征选择、工程设计等多个应用场景中，GGO 展现出卓越的搜索能力与鲁棒性，优于多种现有优化算法，具有广泛的工程实用价值。
该成果于2024年发表在计算机领域一区TOP期刊Expert Systems with Applications上，目前被引用高达521次。
灰雁以其忠诚著称，它们通常与配偶终身伴侣相守，并对幼雏表现出极强的保护意识。当配偶或幼雏生病或受伤时，灰雁会选择留下陪伴，即使在冬季来临、群体南迁的时节也不离不弃。多个灰雁家庭会组成更大的群体，称为“雁群”（Gaggle），群体成员之间会彼此照顾，如下图所示。
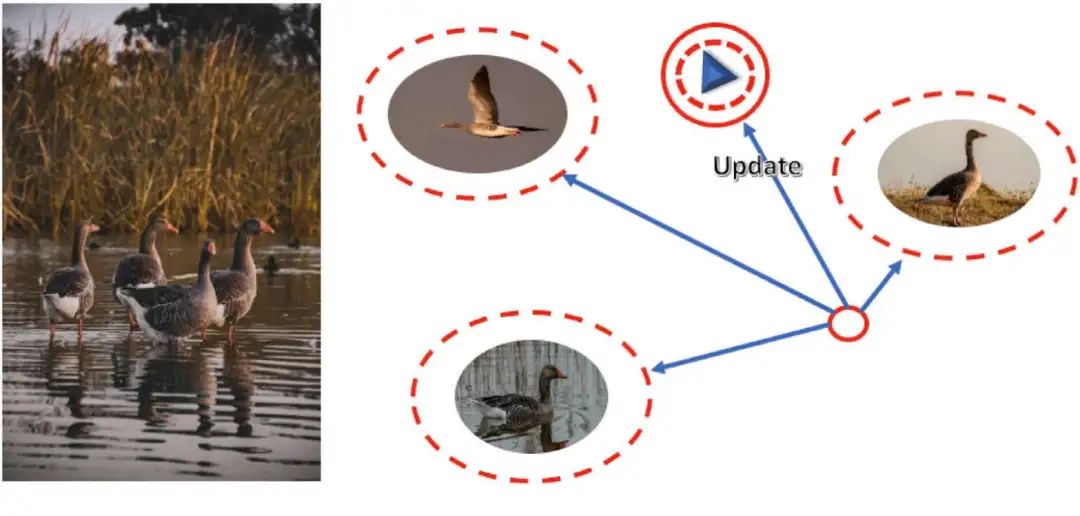
雁群中通常设有一到两个“哨兵”，在大多数成员觅食时，哨兵负责警戒捕食者的出现。哨兵的角色由成员轮流担任，类似船上水手轮班值岗的制度。健康的灰雁会主动照料伤病同伴，受伤的个体也会结成小群体，相互保护，共同觅食。这些体现出高度协作、轮换责任、集群决策和个体之间的信任机制，正是 GGO 算法模拟与建模的核心基础。
1、算法原理
（1）初始化
GGO算法的初始阶段通过随机方式生成多个个体，每个个体代表一个可行解，用于作为问题的候选解。GGO 种群记作 ，其中种群规模 表示一个“雁群”（gaggle）。为评估种群中每个个体的优劣，引入目标函数 。在计算每个个体 的目标函数值后，从中选取最优解，作为“领雁”（leader），记作 。
GGO 算法采用“动态分组”策略，将整个种群划分为两个子群体：探索组（规模为 ）与开发组（规模为 ）。每次迭代过程中，两个子群体的个体数量根据当前最优解的表现动态调整，如下图所示。
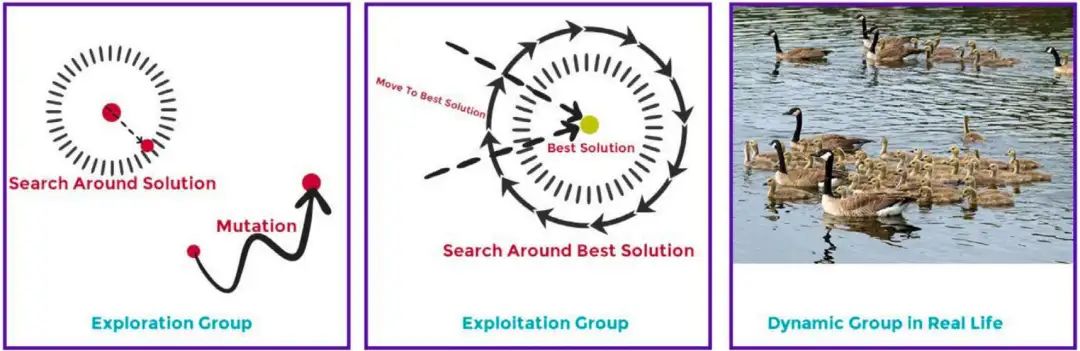
在算法初始化阶段，GGO 以 的比例分配探索与开发组个体。随着迭代进行，探索组中的个体数量 逐渐减少，而开发组中的个体数量 相应增加，以加强对最优解附近区域的局部搜索。然而，当最优解的目标函数值在连续三次迭代中未发生变化时，算法将重新增加探索组中的个体数 ，以扩大搜索范围，尝试跳出局部最优陷阱，寻找新的全局最优解。
（2）探索操作
探索操作负责在搜索空间中定位潜在的优质区域，并通过朝向理想解移动，有效防止算法陷入局部最优。朝向最优解移动：通过采用该策略，探索个体将会在当前位置附近寻找值得探索的新位置。该过程通过反复比较多个周围可能的位置，以适应度为依据选择最优位置来实现。
GGO 算法采用以下公式对向量 和 进行更新，以实现上述操作，其中参数 在迭代过程中从 线性递减至 ：
其中， 表示第 次迭代时的个体位置， 表示当前最优解（领雁）的位置， 表示更新后的个体位置。随机变量 和 的取值范围在 之间，会在每次迭代中随机变化。
为增强搜索的多样性，避免所有个体仅受单一领雁位置影响，GGO 算法选取三个随机搜索个体（paddlings），记作 、 和 ，并基于以下公式更新当前搜索个体的位置，前提是满足 ：
其中， 、 和 的取值范围为 ，并在迭代过程中动态更新。参数 以指数方式递减，其计算公式如下所示：
其中，迭代次数表示为 ， 表示最大迭代次数。第二种更新过程发生在 的条件下，此时参数 和向量 的值会减小，其更新公式如下所示：
其中，参数 为常数， 为取值范围在 内的随机数。参数 在 范围内更新，而 和 的取值范围为 ，并在迭代过程中随机变化。
（3）开发操作
开发组负责改进已有的解决方案。GGO 算法在每个周期结束时识别适应度最高的个体，并给予相应奖励。为了实现开发目标，GGO 采用以下两种策略，具体如下：
朝向最优解移动：采用以下公式沿着最优解方向更新位置。三个哨兵个体 、 和 引导其他非哨兵个体 向猎物的估计位置移动。位置更新过程由以下公式描述。
其中， 、 、 均按照公式 计算， 、 、 按照公式 计算。种群的更新位置 表示为三个解 、 和 的平均值，具体表达如下：
围绕最优解区域搜索：最有潜力的解通常位于飞行中接近最优解（领雁）的位置，这促使部分个体通过探索邻近理想解的区域进行改进，记作 。GGO 算法采用以下公式执行上述搜索过程。
（4）最优解的选择
通过采用变异技术并扫描探索组成员，GGO 展现出卓越的探索能力。强大的探索能力使 GGO 能够有效推迟算法收敛，提升全局搜索效果。算法开始时，输入包括种群规模、变异率及最大迭代次数。随后，GGO 将种群划分为两个子群体：探索组和开发组。GGO 在迭代过程中动态调整两组规模，以不断逼近最优解。每个组分别采用两种策略完成其任务。为了增加多样性和深入搜索，GGO 在迭代间随机调整解的归属，一个解可能从探索组迁移至开发组。GGO 采用精英策略确保最优领雁个体在整个过程始终被保留。
GGO 按照步骤更新探索组（ ）和开发组（ ）的位置。参数 在迭代过程中按如下方式更新：
，
其中， 为当前迭代次数， 为常数， 为最大迭代次数。
每次迭代结束时，GGO 更新搜索空间中的个体位置，并随机打乱个体顺序，以交换探索组与开发组的角色。最终，GGO 返回全局最优解。
GGO优化算法的伪代码如下所示：
2、结果展示
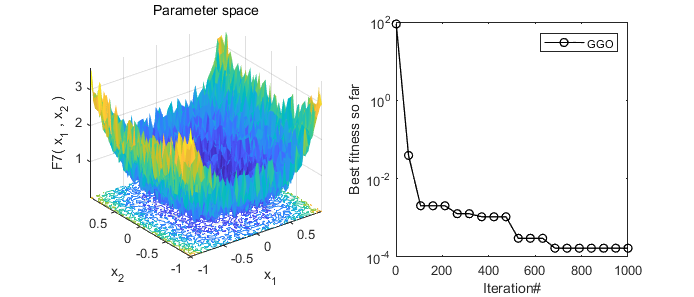
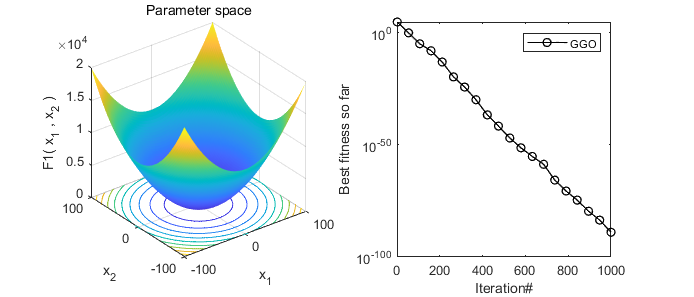
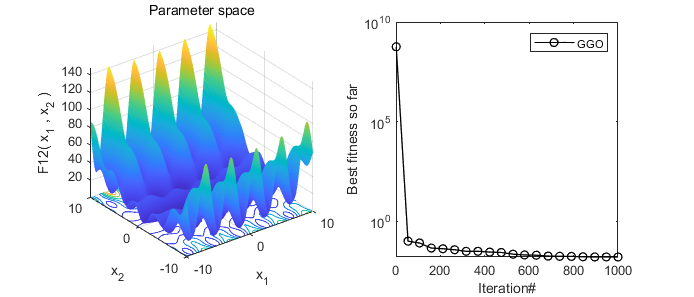
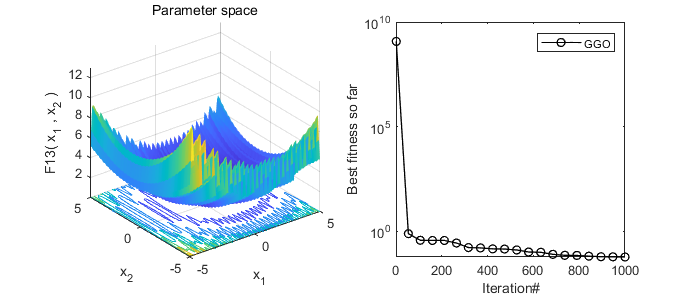
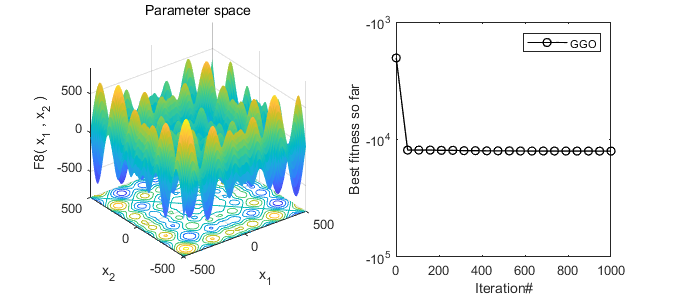
3、MATLAB核心代码
.rtcContent { padding: 30px; } .lineNode {font-size: 14pt; font-family: \"新宋体\", Menlo, Monaco, Consolas, \"Courier New\", monospace; font-style: normal; font-weight: normal; }function [Best_pos, Best_score, Convergence_curve] = GGO(SearchAgents_no, Max_iter, lb, ub, dim, fobj)%___________________________________________________________________%% Greylag Goose Optimization (GGO) Algorithm %% 基于论文: \"Greylag Goose Optimization: Nature-inspired %% optimization algorithm for solving optimization problems\" %% %% 输入参数: %% SearchAgents_no: 搜索代理数量（种群大小） %% Max_iter: 最大迭代次数 %% lb: 下界向量 %% ub: 上界向量 %% dim: 问题维度 %% fobj: 目标函数句柄 %% %% 输出参数: %% Best_pos: 最优解位置 %% Best_score: 最优解适应度值 %% Convergence_curve: 收敛曲线 %%___________________________________________________________________%% 初始化参数a = 2; % 控制参数a，从2线性递减到0c = 2; % 常数参数b = 1; % 螺旋常数% 初始化种群X = initialization(SearchAgents_no, dim, ub, lb);% 计算初始适应度fitness = zeros(1, SearchAgents_no);for i = 1:SearchAgents_no fitness(i) = fobj(X(i, :));end% 找到最优解[Best_score, best_idx] = min(fitness);Best_pos = X(best_idx, :);% 初始化收敛曲线Convergence_curve = zeros(1, Max_iter);% 初始化探索和开发组n1 = round(SearchAgents_no * 0.5); % 探索组初始大小n2 = SearchAgents_no - n1; % 开发组初始大小% 记录最优解未改善的次数no_improvement_count = 0;prev_best_score = Best_score;% 主循环for t = 1:Max_iter % 更新控制参数 a = 2 - t * (2 / Max_iter); % a从2线性递减到0 % 更新z参数（指数递减） z = 1 - (t / Max_iter)^2; % 随机打乱种群以交换角色 rand_indices = randperm(SearchAgents_no); X = X(rand_indices, :); fitness = fitness(rand_indices); % 更新探索组 (前n1个个体) for i = 1:n1 % 计算A和C向量 r1 = rand(); r2 = rand(); r3 = rand(); r4 = rand(); r5 = rand(); A = 2 * a * r1 - a; C = 2 * r2; % 更新权重参数 w1 = 2 * rand(); w2 = 2 * rand(); w3 = 2 * rand(); w4 = 2 * rand(); if mod(t, 2) == 0 if r3 < 0.5 if abs(A) < 1 % 向最优解移动 X(i, 
= Best_pos - A .* abs(C .* Best_pos - X(i, :)); else % 使用三个随机代理更新位置 paddle_indices = randperm(SearchAgents_no, 3); X_paddle1 = X(paddle_indices(1), :); X_paddle2 = X(paddle_indices(2), :); X_paddle3 = X(paddle_indices(3), :); X(i, = w1 * X_paddle1 + z * w2 * (X_paddle2 - X_paddle3) + ... (1 - z) * w3 * (X(i, - X_paddle1); end else % 螺旋更新 l = 2 * rand() - 1; % l在[-1,1]之间 X(i, = w4 * abs(Best_pos - X(i, :)) .* exp(b * l) .* cos(2 * pi * l) + ... (2 * w1 * (r4 + r5)) * Best_pos; end else % 在最优解周围搜索 D = rand(1, dim); w = rand(); X_flock1 = X(randi(SearchAgents_no), :); X(i, = X(i, + D .* (1 + z) * w .* (X(i, - X_flock1); end end [~, sorted_indices] = sort(fitness); indices_of_min3 = sorted_indices(1:3); % 更新开发组 (后n2个个体) for i = (n1 + 1):SearchAgents_no if mod(t, 2) == 0 % 选择三个哨兵 X_sentry1 = X(indices_of_min3(1), :); X_sentry2 = X(indices_of_min3(2), :); X_sentry3 = X(indices_of_min3(3), :); % 计算A和C向量 r1_1 = rand(); r1_2 = rand(); r1_3 = rand(); r2_1 = rand(); r2_2 = rand(); r2_3 = rand(); A1 = 2 * a * r1_1 - a; A2 = 2 * a * r1_2 - a; A3 = 2 * a * r1_3 - a; C1 = 2 * r2_1; C2 = 2 * r2_2; C3 = 2 * r2_3; % 计算三个位置 X1 = X_sentry1 - A1 .* abs(C1 .* X_sentry1 - X(i, :)); X2 = X_sentry2 - A2 .* abs(C2 .* X_sentry2 - X(i, :)); X3 = X_sentry3 - A3 .* abs(C3 .* X_sentry3 - X(i, :)); % 更新位置（三个位置的平均值） X(i, = (X1 + X2 + X3) / 3; else % 在最优解周围搜索 D = rand(1, dim); w = rand(); X_flock1 = X(indices_of_min3(1), :); X(i, = X(i, + D .* (1 + z) * w .* (X(i, - X_flock1); end end % 边界检查 for i = 1:SearchAgents_no X(i, = max(X(i, :), lb); X(i, = min(X(i, :), ub); end % 重新计算适应度 for i = 1:SearchAgents_no fitness(i) = fobj(X(i, :)); end % 更新最优解 [current_best, best_idx] = min(fitness); if current_best < Best_score Best_score = current_best; Best_pos = X(best_idx, :); end % 动态调整探索和开发组大小 if abs(Best_score - prev_best_score) = 3 n1 = min(n1 + 1, SearchAgents_no - 1); n2 = SearchAgents_no - n1; no_improvement_count = 0; else % 否则逐渐减少探索组，增加开发组 if n1 > 1 n1 = max(1, n1 - 1); n2 = SearchAgents_no - n1; end end prev_best_score = Best_score; % 记录收敛曲线 Convergence_curve(t) = Best_score; % 显示进度 if mod(t, 10) == 0 fprintf(\'Iteration %d: Best Score = %.6e, Exploration Group Size = %d\\n\', ... t, Best_score, n1); endendfprintf(\'GGO Algorithm completed. Best Score = %.6e\\n\', Best_score);endfunction X = initialization(SearchAgents_no, dim, ub, lb)%初始化种群Boundary_no = size(ub, 2); % 边界数量% 如果边界是标量，扩展为向量if Boundary_no == 1 X = rand(SearchAgents_no, dim) .* (ub - lb) + lb;else for i = 1:dim ub_i = ub(i); lb_i = lb(i); X(:, i) = rand(SearchAgents_no, 1) .* (ub_i - lb_i) + lb_i; endendend参考文献
[1] El-Kenawy E S M, Khodadadi N, Mirjalili S, et al. Greylag goose optimization: nature-inspired optimization algorithm[J]. Expert Systems with Applications, 2024, 238: 122147.
完整代码获取
后台回复关键词：
TGDM876
获取更多代码：
或者复制链接跳转：https://docs.qq.com/sheet/DU3NjYkF5TWdFUnpu
