从0开始学习R语言--Day57--SCAD模型

在之前，我们提到过对于基因数据，我们会倾向于用弹性网络去建模，这样可以做到节省大量计算量的同时，保留关键的变量做筛选；但是实际上弹性网络本质上是用两种方法的结合去拟合，得到的函数是凸函数，从而不可避免的会产生偏差。

相比之下，SCAD则选择更直接的分段建模，这样可以最大程度地保留原有特征的特点，同时做到更优的筛选，只是计算复杂度会更高，需要谨慎使用。

以下是一个例子：

# 加载必要的包library(ncvreg)library(ggplot2)# 生成模拟数据集set.seed(123)n <- 200p <- 10X <- matrix(rnorm(n * p), n, p)colnames(X) <- paste0(\"X\", 1:p)true_beta <- c(3, 1.5, 2, rep(0, p-3))y <- X %*% true_beta + rnorm(n, sd = 1.5)# 使用SCAD进行变量选择scad_fit <- ncvreg(X, y, penalty = \"SCAD\")# 使用交叉验证选择最优λcv_fit <- cv.ncvreg(X, y, penalty = \"SCAD\")# 查看交叉验证结果#print(cv_fit)# 获取最优λ值 (这里使用最小化误差的λ)best_lambda <- cv_fit$lambda.min# 查看最优模型的摘要summary(scad_fit, lambda = best_lambda)# 查看最优模型的系数coef(scad_fit, lambda = best_lambda)# 绘制系数路径图plot(scad_fit)abline(v = log(best_lambda), lty = 2, col = \"red\")  # 标记最优λ位置# 可视化比较results <- data.frame(  Variable = colnames(X),  True = true_beta,  SCAD = coef(scad_fit, lambda = best_lambda)[-1]  # 去掉截距项)ggplot(results, aes(x = Variable)) +  geom_point(aes(y = True, color = \"True\"), size = 3) +  geom_point(aes(y = SCAD, color = \"SCAD\"), size = 3) +  labs(title = paste(\"真实系数与SCAD估计比较 (λ =\", round(best_lambda, 4), \")\"),       y = \"系数值\",       color = \"类型\") +  theme_minimal()

输出：

SCAD-penalized linear regression with n=200, p=10At lambda=0.3861:-------------------------------------------------  Nonzero coefficients         :   3  Expected nonzero coefficients:   0.00  Average mfdr (3 features)    :   0.000   Estimate     z    mfdr SelectedX1    3.003 30.39 < 1e-04        *X3    2.014 20.85 < 1e-04        *X2    1.547 16.53 < 1e-04        *(Intercept)          X1          X2          X3          X4          X5          X6          X7  -0.1908806   3.0030121   1.5470496   2.0140936   0.0000000   0.0000000   0.0000000   0.0000000          X8          X9         X10   0.0000000   0.0000000   0.0000000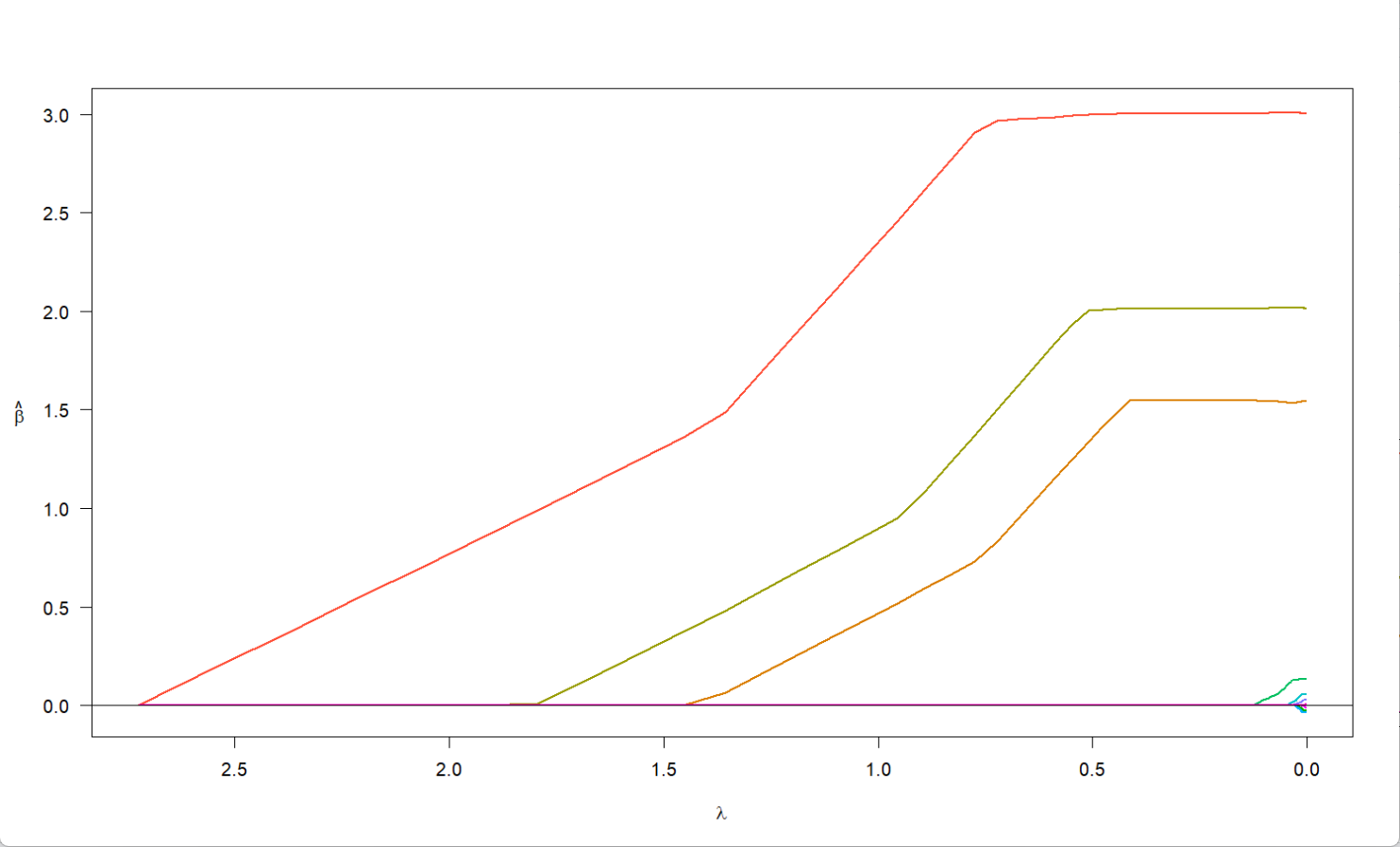 

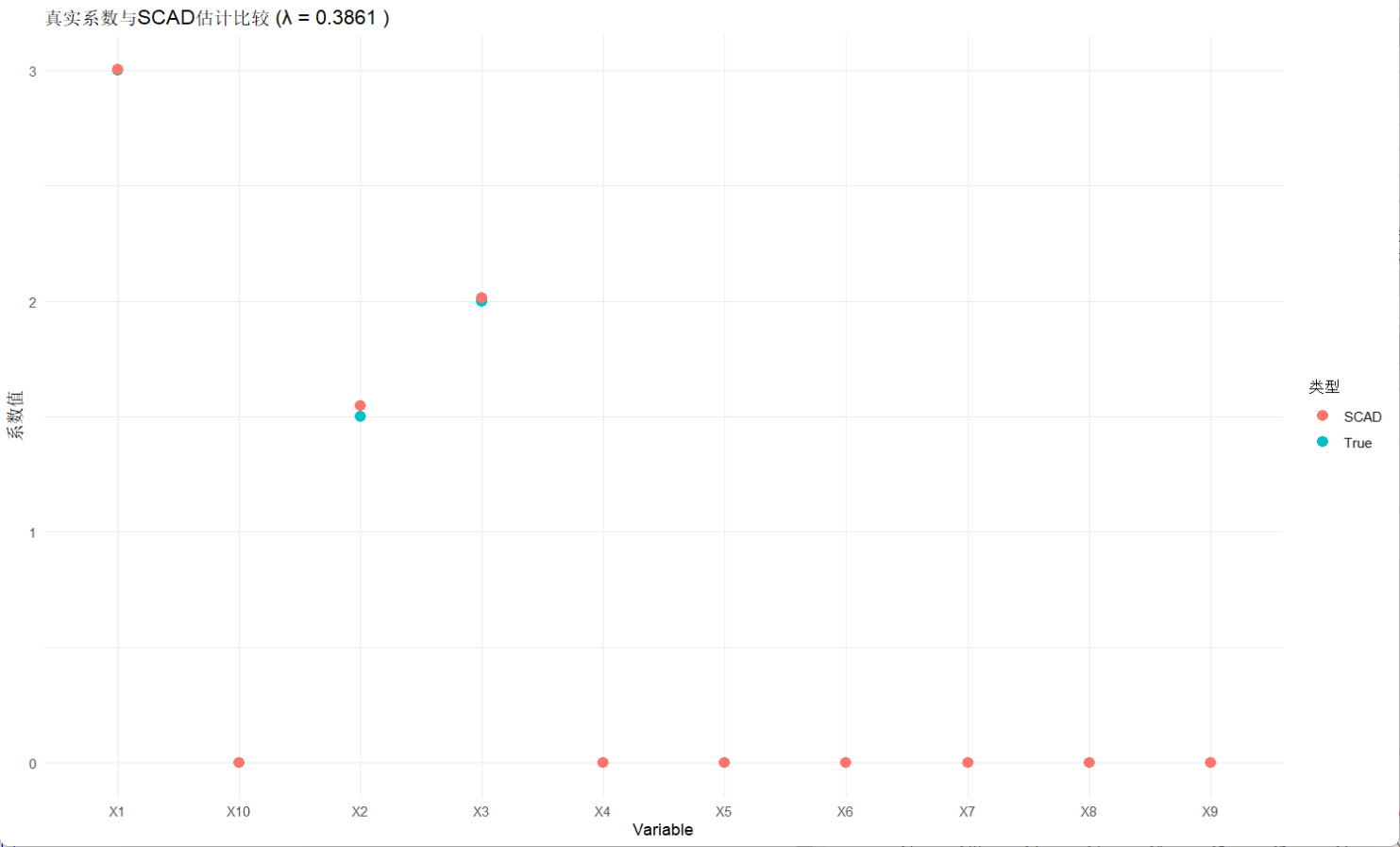
结果表明，X1、X2、X3系数非零，且mfdr < 1e-04，统计学显著，是显著变量；mdfr值极低，说明假阳性的风险极低；当lambda较大时，系数基本被压缩为0，说明模型趋于稀疏；而lambda在减少时，系数先快速上升再逐渐趋于平缓，说明其具有收敛性和稳定性。