网站导航
> 技术文档 > 【深度学习】通俗易懂的基础知识：指数加权平均

【深度学习】通俗易懂的基础知识：指数加权平均

网友: 技术文档 2025-08-08 03:45:26

一、什么是指数加权平均？

        指数在数学中表示一个数的幂次运算（如aⁿ中的n），而在统计学中特指随时间变化的几何衰减系数，加权指对不同数据赋予不同权重，使重要数据对结果产生更大影响。指数加权平均指是一种时间序列数据的加权计算方法，其特点是随着时间推移，数据权重呈指数级衰减——近期数据具有更高权重，而早期数据影响逐渐减弱。该方法的核心在于\"动态平衡历史与当前数据，同时突出近期信息的可靠性\"。

二、什么叫数据权重呈指数级衰减？

        我在之前写过的一篇文章【人工智能】神经网络的优化器optimizer（一）：Momentum动量优化器中有所提及，现在先把神经网络中指数加权平均的公式贴出来：

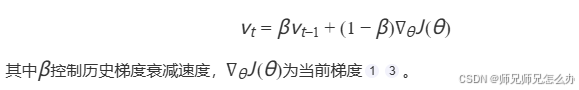
        展开推导如下：

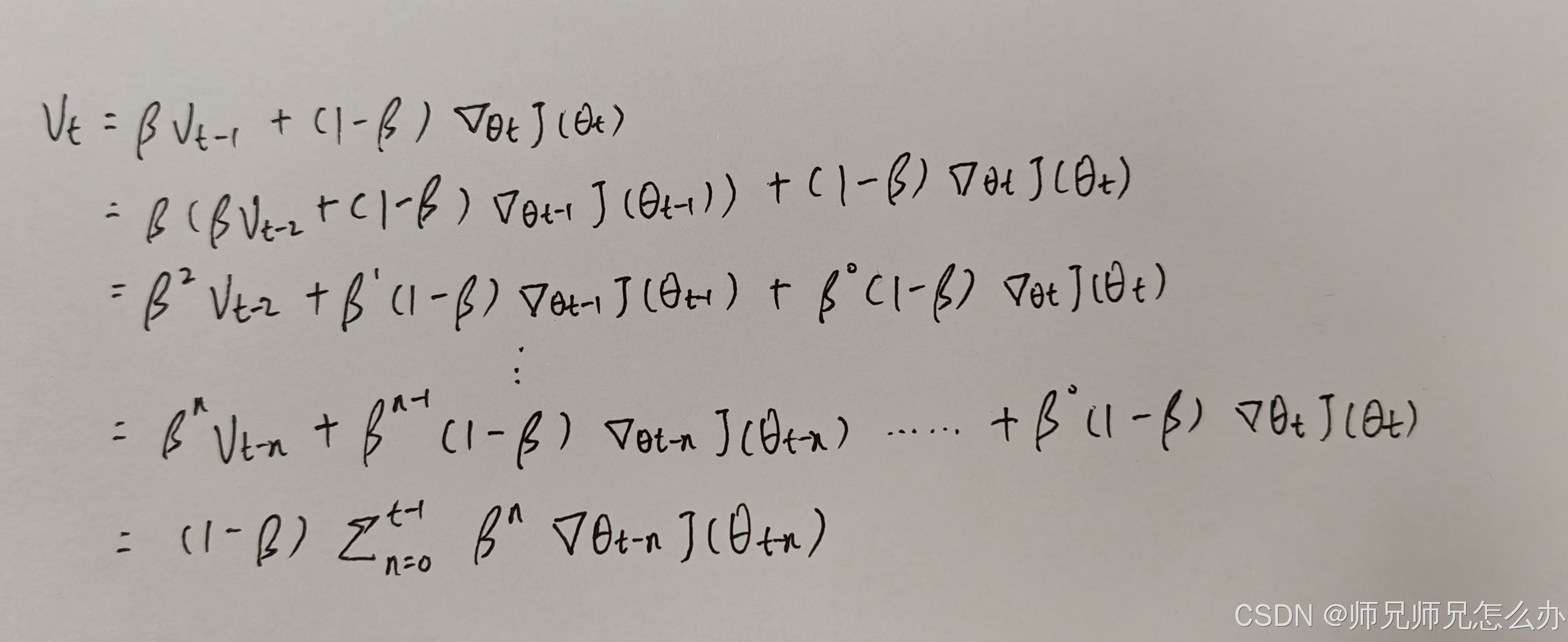
         基于以上公式，我们可以假设下：

          可以看到，越远的梯度权重呈现指数级衰减。

三、数学推导‌

        抛开神经网络单纯讲指数加权平均的核心公式为：

        v_{t}=β⋅v_{t-1}+(1−β)⋅x_{t}

其中：

  • v_{t}：当前时刻的加权平均值
  • v_{t-1}：上一时刻的加权平均值（初始值 v_{0}=0）
  • x_{t}：想要观察的时刻 t 的值
  • \\beta：衰减因子（0<β<1），控制历史数据的权重分布‌

        ‌推导过程‌

        递推展开‌（假设 v_{0}=0）：

v_{1}=(1−β)⋅x_{1}

v_{2}=β⋅v_{1}+(1−β)⋅x_{2}=β(1−β)x_{1}+(1−β)x_{2}

v_{3}=β⋅v_{2}+(1−β)⋅x_{3}=β^{2}(1−β)x_{1}+β(1−β)x_{2}+(1−β)x_{3}

 ⋮

 ⋮

v_{t}=(1-\\beta)[x_{t}+\\beta x_{t-1} + \\beta^{2} x_{t-2} + ...... +\\beta^{t-1} x_{1}]

        ‌权重系数规律‌：
        从展开式可见，历史数据 x_{k}的权重为 (1−β)β^{t-k}。权重随 k（时间距离）增大而‌指数衰减‌：

  • 当前时刻 x_{t}：权重 =(1−β)
  • 前一时刻 x_{t-1}：权重 =(1−β)β
  • 前 n 时刻x_{t-n}：权重 =(1−β)β^{n}
  • 权重总和收敛于1‌：\\sum_{k=0}^{t-1}(1-\\beta)\\beta^{k}=(1-\\beta)^\\frac{1-\\beta^{t}}{1-\\beta}=1-\\beta^{t}\\rightarrow 1  (当 t→∞)‌

四、权重的取值

        那么我们的权重究竟取多少是合适的呢？其实并没有一个具体的值可以确定，需要根据不同的情况确定不同的值，大概的范围如下：

β 值 平滑性 响应速度 典型曲线特征 0.98（最大） ‌极高‌ ‌极慢‌ 平坦，滞后实际变化 0.9（适中） 中等 中等 平衡平滑与响应，历史数据权重衰减慢，平均结果更平滑，但响应延迟明显。 0.5（较小） ‌极低‌ ‌极快‌ 抖动明显，紧跟最新数据，近期数据主导，对波动更敏感，但噪声抑制弱。

        以下通过一个例子：正弦波加噪声数据，来对比β=0.1/0.5/0.9/0.98 时的平滑效果：

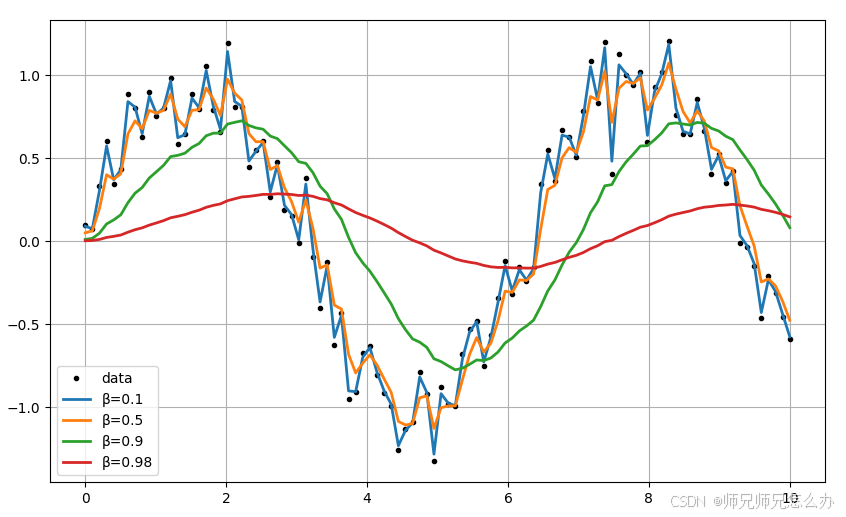
        可以观察到以下几个规律：

β=0.1（蓝线）：几乎跟随噪声波动，响应快但平滑效果差

β=0.5（橙线）：平衡噪声抑制与趋势跟踪

β=0.9（绿线）：极度平滑但明显滞后原始信号峰值

β=0.98（红线）：滞后严重

        β越小曲线越贴近原始数据，β越大平滑效果越强但滞后越明显。

        代码如下：

import numpy as npimport matplotlib.pyplot as plt# 生成模拟数据（正弦波+噪声）np.random.seed(42)t = np.linspace(0, 10, 100)data = np.sin(t) + np.random.normal(0, 0.2, 100)def ewma(data, beta): v = [0] # 初始化v0 for x in data: v.append(beta * v[-1] + (1 - beta) * x) return v[1:] # 去掉初始v0# 计算不同β值的EWMAbeta_list = [0.1, 0.5, 0.9,0.98]results = {f\'β={beta}\': ewma(data, beta) for beta in beta_list}# 可视化plt.figure(figsize=(10, 6))plt.plot(t, data, \'k.\', label=\'data\')for label, result in results.items(): plt.plot(t, result, label=label, linewidth=2)plt.legend()plt.grid(True)plt.show()

五、指数加权平均和普通平均的区别

        我们通过一个简单的例子说明：

（一）假设你连续10天记录的气温数据为：[22, 23, 24, 25, 26, 27, 28, 29, 30, 31]℃：

普通平均：将所有温度相加后除以天数
(22+23+24+25+26+27+28+29+30+31)/10 = 26.5℃
这种方法赋予每天相同权重，但会稀释近期温度变化的影响。

指数加权平均（衰减因子β=0.5）：
第10天权重：50%（31×0.5=15.5）
第9天权重：25%（30×0.25=7.5）
第8天权重：12.5%（29×0.125≈3.6）
...
最终加权值≈15.5+7.5+3.6+1.8+0.9+0.4+0.2+0.1+0.05+0.02≈30.1℃

        对比可见：这种计算明显更贴近近期升温趋势（第10天31℃），而普通平均则被早期低温数据拉低。由此可知指数加权平均对短期变化更敏感，适合捕捉天气趋势；普通平均则更适合分析长期稳定状态。

网络标签：

相关问题