进阶——数据结构（针对小白版）_线性表,树,图+1对1,1对n,n对n

一、基本概念及顺序表

1、逻辑结构

集合（数据在同一个集合中，关系平等）、线性（一对一的关系）、树（一对多的关系）、图（多对多的关系）

2、物理结构（数据的逻辑结构在计算机中的存储形式）

顺序存储：数据存放在连续的存储单位中。逻辑关系和屋里关系一致。

链式存储：数据存放的存储单位是随机或随意的，可以连续也可以不连续。

3、相关概念

数据—（变量），数据项，数据元素，数据对象

struct Per //数据元素{char name; //数据项int age;char phone;}struct Per list[100]; //数据对象

4、数据的类型：是指一组性质相同的值的集合及定义在此集合上的一些操作的总称

原子类型，int，char，float

结构类型，sturct， union

ADT：抽象数据类型（数学模型+操作）

5、程序 =  数据 + 算法。

算法是解决特定问题求解步骤的描述，计算机中表现为指令的有限序列，每条指令表示一个或多个操作。

算法特征：输入，输出、有穷性、确定性、可行性

算法设计：正确性、可读性、健壮性、高效

6、算法时间复杂度：执行算法所花时间的度量（O）

推导时间复杂度（用1取代所有常数，只保留最高阶，最高阶存在且不是1则去除最高阶的常数）

O(1)<O(logn)<O(N)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)（最好到最坏）

7、线性表（顺序表和链表）

零个或多个数据元素的有限序列
元素之间是有顺序了。如果存在多个元素，第一个元素无前驱，最有一个没有后继，其他的元素只有一个前驱和一个后继。

当线性表元素的个数n（n>=0）定义为线性表的长度，当n=0时，为空表。在非空的表中每个元素都有一个确定的位置，如果a1是第一个元素，那么an就是第n个元素。

8、顺序表

• 8.1 定义

typedef struct { char name[20]; char sex; int age; int score;}PER;typedef PER DATATYPE;typedef struct{ DATATYPE *head;// 数组的数组名 存储datatype 类型的数据 int tlen;// 数组的容量 int clen; // 数组中有效元素的个数}SeqList;// 顺序表 表头结构

理解：

head是指向 PER 结构体数组的指针，tlen就是数组的长度，clen就是数组得到有效数据。

然后定义了一个包含姓名、性别等属性的结构体，这个结构体用typedef定义出一DATATYPE的数据类型

然后用DATATYPE数据类型来定义head这个指针数组

然后定义了一个包含head，tlen，clen的结构体，SeqList是一个数据类型

• 8.2 创建

SeqList *CreateSeqList(int n){ SeqList *sl=malloc(sizeof(SeqList)); if(NULL==sl) { fprintf(stderr,\"CreateSeqList malloc error\\n\");//stderr专门输出错误信息的 return NULL; } sl->head=malloc(sizeof(DATATYPE)*n); if(NULL==sl->head) { fprintf(stderr,\"CreateSeqList malloc2 error\\n\"); return NULL; } sl->tlen=n; sl->clen=0; return sl;}

• 8.3 插入

int IsFullSeqList(SeqList *sl){ return sl->tlen==sl->clen;}int InsertTailSeqList(SeqList* sl, DATATYPE* data) { if(IsFullSeqList(sl)) { return 1; } //把sl->clen放到sl-head memcpy(&(sl->head[sl->clen]),data,sizeof(DATATYPE)); sl->clen++; return 0; }

• 8.4 遍历

int GetSizeSeqList(SeqList *sl){ return sl->clen;}int ShowSeqList(SeqList *sl){ int size= GetSizeSeqList(sl); for (int i=0;ihead[i].name,sl->head[i].sex,sl->head[i].age,sl->head[i].score); } return 0; }

• 8.5 指定位置插入

int InsertPosSeqList(SeqList *sl, DATATYPE* data, int pos){ if(IsFullSeqList(sl)) { return 1; } if(pos > sl->clen || pos<0) { return 1; } if(pos clen) { int i; for (i=sl->clen;i>pos;i--)//sl->clen是当前元素的下一个位置 { sl->head[i]=sl->head[i-1]; } memcpy(&(sl->head[pos]),data,sizeof(DATATYPE)); sl->clen++; } return 0;}

tips:

pos=s->slen时

那么循环首先i=sl->clen，循环条件i>pos不成立，所以循环不执行，直接进行赋值

• 8.6 查找

int FindSeqListByName(SeqList *sl,char* name){ int size=GetSizeSeqList(sl); for(int i=0;ihead[i].name,name)==0) { return i; } } return -1;}

• 8.7 修改

int ModifySeqList(SeqList *sl,char *old,DATATYPE*data){ int ret=FindSeqListByName(sl, old); if(ret==-1) { return 1; } memcpy(&sl->head[ret], data, sizeof(DATATYPE)); return 0;}

• 8.8 删除

int DeleteSeqList(SeqList *sl,char *name){ int ret=FindSeqListByName(sl, name); if(ret==-1) { return 1; } int i=0; int size=GetSizeSeqList(sl); for (i=ret;ihead[i], &sl->head[i+1], sizeof(DATATYPE)); } sl->clen--; return 0;}

• 8.9 清空

int ClenSeqList(SeqList *sl){ sl->clen=0; return 0;}

• 8.10 销毁

int DestroySeqList(SeqList *sl){ free(sl->head); free(sl); return 0;}

优缺点

优点：

1、无需为表中的逻辑关系增加额外的存储空间

2、可以快速随机访问元素O(1)

缺点：

1、插入，删除元素需要移动元素O(n)

2、无法动态存储

二、链表的基本操作

***(单向链表复习写代码时，写一下给按任意类型来查找，手撕代码顺序，链式，栈，队列)

1、链表的相关概念

• 线性表的链式存储：解决顺序存储的缺点：插入和删除，动态存储问题
• 线性表链式存储结构的特点是一组任意的存储单位存储线性表的数据元素，存储单元可以是连续的，也可以不连续。可以被存储在任意内存未被占用的位置上。
• 所以前面的顺序表只需要存储数据元素信息就可以了。在链式结构中还需要一个元素存储下一个元素的地址。
• 为了表示每个数据元素，ai与其直接后继数据元素ai+1之间的逻辑关系、对a来说，除了存储其本身的信息外，还需要存一个指示器直接后续的信息。把存储元毒信息的域叫数据域，把存储直接后继位置的域叫指针域。这两部分信息组成数据元素ai的存储映像，叫结点(Node);

 2、单向链表

2.1 定义

typedef struct { char name[20]; char sex; int age; int score;}DATATYPE;typedef struct node{ DATATYEP data; struct node *next;}LinkNodetypedef struct{ DATATYPE *head;// 数组的数组名 存储datatype 类型的数据 int clen; // 数组中有效元素的个数}LinkList;// 顺序表 表头结构

2.2 创建

LinkList *CreateLinkList(){ LinkList *ll=malloc(sizeof(LinkList)); if(ll==NULL) { fprintf(stderr, \"CreateLinkList malloc\\n\"); return NULL; } ll->head=NULL; ll->clen=0; return ll;}

2.3 头插入（O(1)，对顺序没有要求）

int IsEmptyLinkList(LinkList *list){ return list->clen==0;}int InsertHeadLinkList(LinkList *list, DATATYPE *data){ LinkNode* newnode=malloc(sizeof(LinkNode)); if(newnode==NULL) { fprintf(stderr, \"CreateLinkList malloc\\n\"); return 1; } memcpy(&newnode->data, data, sizeof(DATATYPE)); newnode->next=NULL; if (IsEmptyLinkList(list)) { list->head=newnode; }else { newnode->next=list->head; list->head=newnode; } list->clen++; return 0;}

2.4 尾插：O(n)

int InsertTailLinkList(LinkList *list, DATATYPE *data){ LinkNode* newnode=malloc(sizeof(LinkNode)); if(newnode==NULL) { fprintf(stderr, \"CreateLinkList malloc\\n\"); return 1; } memcpy(&newnode->data, data, sizeof(DATATYPE)); newnode->next=NULL; if (IsEmptyLinkList(list)) { InsertHeadLinkList(list, data); return 0; //list->head=newnode; }else { LinkNode* tmp=list->head; while (tmp->next) { tmp=tmp->next; } tmp->next=newnode; } list->clen++; return 0;}

2.5 遍历

int ShowLinkList(LinkList *list){ LinkNode* tmp=list->head; while (tmp!=NULL) { printf(\"name:%s age:%d sex:%c score:%d\\n\",tmp->data.name,tmp->data.age,tmp->data.sex,tmp->data.score); tmp= tmp->next;//tmp++;  } return 0;}

2.6 查找

LinkNode *FindLinkList(LinkList *list, char *name){ if(IsEmptyLinkList(list)) { return NULL; } LinkNode* tmp=list->head; while(tmp) { if(strcmp(tmp->data.name,name)==0) { return tmp; } tmp=tmp->next; } return NULL;}

2.7 修改

int ModifyLinkList(LinkList *list, char *name, DATATYPE *data){ LinkNode *tmp=FindLinkList(list, name); if(tmp==NULL) { return 1; } memcpy(&tmp->data,data,sizeof(DATATYPE)); return 0;}

2.8 删除

int DeleteLinkList(LinkList *list, char *name){ LinkNode *prev=list->head; LinkNode *tmp=list->head; if(IsEmptyLinkList(list)) { return 1; }//如果删除的是头节点 if(strcmp(name, tmp->data.name)==0) { list->head=tmp->next; free(tmp); list->clen--; return 0; }//如果是其他节点：从第二个节点开始遍历，通过 prev->next 检查下一个节点是否匹配。找到匹配节点后，修改前驱节点的 next 指针以跳过待删除节点，然后释放内存。 while (prev->next) { if (strcmp(prev->next->data.name, name)==0) { tmp=prev->next; prev->next=tmp->next; free(tmp); list->clen--; return 0; } prev=prev->next; //重要 } return 0;}

2.9 销毁

int GetSizeLinkList(LinkList *list){ return list->clen;}int DestroyLinkList(LinkList *list){ int size=GetSizeLinkList(list); for(int i=0;ihead; list->head=list->head->next; free(tmp); } free(list); return 0;}

易错点：

字符串本身就是指针

整数是值类型，必须转成指针传递

C语言解决类型不定的方法：void*

3、单向链表的练习

3.1 寻找单向链表的倒数第k个节点

LinkNode *FindLastKNode(LinkList *list,int k){ int size=GetSizeLinkList(list); if(size<k||khead; LinkNode* slow=list->head;//定义两个快慢指针，指向链表的头 for(int i=0;inext; } while (fast)//当快指针走到空时，慢指针就刚好走到k的位置 { fast=fast->next; slow=slow->next; } return slow;}

3.2 单向链表返回中间节点

LinkNode *FindMidNode(LinkList *list){ LinkNode* fast=list->head; LinkNode* slow=list->head;//定义两个快慢指针 while (fast) { fast=fast->next; if(fast==NULL) { break; } slow=slow->next; fast=fast->next; }//循环：快指针走一步，然后判断快指针是否为空，为空则退出循环，接着慢指针走一步，最后快指针再走一步，实现快指针走两步，慢指针走一步，就可以返回中间值 return slow;}

3.3 单向链表的逆序

LinkList *RverseLinkList(LinkList *list){ int size=GetSizeLinkList(list); if(sizehead; //当前要处理的节点，初始指向头节点 LinkNode* Next=tmp->next; //保存下一个节点，初始为tmp->next while (1) { tmp->next=prev; //将当前节点的next指向前一个节点 prev=tmp; //prev往后走 tmp=Next; //tmp往后走 if(tmp==NULL) { break; } //tmp走完后，此时就要判断tmp是否为空 Next=Next->next;//Next往后走 } list->head=prev;//更新链表的头节点为prev（此时prev指向原链表的尾节点，即新链表的头节点） return list;}

4、 顺序表和链表优缺点

• 存储方式

顺序表是一段连续的存储单元
链表是逻辑结构连续物理结构（在内存中的表现形式）不连续

• 时间性能

查找 ：

        顺序表O(1)
         链表  O(n)

插入和删除：
        顺序表 O(n)
        链表   O(1)

• 空间性能

顺序表 需要预先分配空间，大小固定
链表， 不需要预先分配，大小可变，动态分配

5、双向链表

5.1 定义

typedef struct{ char name[32]; char sex; int age; int score;} DATATYPE;typedef struct dounode{ DATATYPE data; struct dounode *prev; struct dounode *next;} DouLinkNode;typedef struct { DouLinkNode *head; int clen;} DouLinkList;

5.2 创建

DouLinkList *CreateDouLinkList(){ DouLinkList *dl=malloc(sizeof(DouLinkList)); if(dl==NULL)//? { fprintf(stderr, \"CreateDouLinkList malloc\\n\"); return NULL; } dl->head=NULL; dl->clen=0; return dl;}

5.3 头插

int IsEmptyDouLinkList(DouLinkList *dl) //判断是否为空{ return dl->clen==0;}int InsertHeadDouLinkList(DouLinkList *dl, DATATYPE *data){ DouLinkNode* newnode=malloc(sizeof(DouLinkNode)); if(newnode==NULL) { fprintf(stderr, \"CreateDouLinkList malloc\\n\"); return 1; } memcpy(&newnode->data, data, sizeof(DATATYPE)); newnode->next=NULL; newnode->prev=NULL; if(IsEmptyDouLinkList(dl)) { dl->head=newnode;//? }else//? { newnode->next=dl->head;// 新节点的 next 指向原头节点 dl->head->prev=newnode;// 原头节点的 prev 指向新节点 dl->head=newnode;// 更新链表头指针为新节点 } dl->clen++; return 0;}

5.4 尾插

int InsertTailDouLinkList(DouLinkList *dl, DATATYPE *data){ if (IsEmptyDouLinkList(dl)) { return InsertHeadDouLinkList(dl, data); //list->head=newnode; } DouLinkNode* newnode=malloc(sizeof(DouLinkNode));//调用头节点已经申请了一个空间，所以在后面申请 if(newnode==NULL) { fprintf(stderr, \"CreateLinkList malloc\\n\"); return 1; } memcpy(&newnode->data, data, sizeof(DATATYPE)); newnode->next=NULL; newnode->prev=NULL; DouLinkNode* tmp=dl->head; while (tmp->next) { tmp=tmp->next; } newnode->prev=tmp; tmp->next=newnode; dl->clen++; return 0;}

5.5 任意位置插

int InsertPosDouLinkList(DouLinkList* dl, DATATYPE* data, int pos){ int size=GetSizeDouLinkList(dl); if(pos==0) { return InsertHeadDouLinkList(dl, data); }else if(pos==size) { return InsertTailDouLinkList(dl, data); }else { DouLinkNode* tmp=dl->head; for(int i=0;inext; } DouLinkNode* newnode=malloc(sizeof(DouLinkNode)); if(newnode==NULL) { fprintf(stderr, \"CreateLinkList malloc\\n\"); return 1; } memcpy(&newnode->data, data, sizeof(DATATYPE)); newnode->next=NULL; newnode->prev=NULL; newnode->next=tmp->next; newnode->prev=tmp; tmp->next->prev=newnode; tmp->next=newnode; dl->clen++; return 0;  }}

5.6 遍历

int GetSizeDouLinkList(DouLinkList *dl){ return dl->clen;}int ShowDouLinkList(DouLinkList *dl,SHOW_DIR dir){ int size=GetSizeDouLinkList(dl); DouLinkNode* tmp=dl->head; if(DIR_FORWARD==dir) { for(int i=0;idata.name,tmp->data.age,tmp->data.sex,tmp->data.score); tmp= tmp->next;//tmp++; } }else { while (tmp->next) { tmp=tmp->next; } for(int i=0;idata.name,tmp->data.age,tmp->data.sex,tmp->data.score); tmp= tmp->prev;//tmp++; } } return 0;}

 5.7 查找

DouLinkNode *FindDouLinkList(DouLinkList *dl, char *name){ if(IsEmptyDouLinkList(dl)) { return NULL; } DouLinkNode* tmp=dl->head; while(tmp) { if(strcmp(tmp->data.name,name)==0) { return tmp; } tmp=tmp->next; } return NULL;}

5.8 修改

int ModifyDouLinkList(DouLinkList *dl, char *name, DATATYPE *data){ DouLinkNode *tmp=FindDouLinkList(dl, name); if(tmp==NULL) { return 1; } memcpy(&tmp->data,data,sizeof(DATATYPE)); return 0;}

5.9 删除

int DeleteDouLinkList(DouLinkList *dl, char *name){ DouLinkNode *tmp=FindDouLinkList(dl, name); if(tmp==NULL) { return 1; } if(tmp==dl->head) { dl->head=dl->head->next; if(dl->head->prev) { dl->head->prev=NULL; } }else { //if(tmp->next) { tmp->next->prev=tmp->prev; } tmp->prev->next=tmp->next; } free(tmp); dl->clen--; return 0;}

5.10 销毁

DouLinkList *RverseDouLinkList(DouLinkList *dl){ int size=GetSizeDouLinkList(dl); if(sizehead; DouLinkNode* Next=Tmp->next; while (1) { Tmp->next=Prev; Tmp->prev=Next; Prev=Tmp; Tmp=Next; if(Tmp==NULL) { break; } Next=Next->next; } dl->head=Prev; return dl;}

三、栈、队列

1、栈的概念

栈是限定仅在表尾进行插入和删除操作的线性表，先进后出，后进先出

栈顶：允许操作的一端

栈底：不允许操作的一端

顺序存储的栈和链式存储的栈

2、栈

2.1 定义

typedef struct{ char name[32]; char sex; int age; int score;} DATATYPE;typedef struct stacknode{ DATATYPE data; struct stacknode *next;} LinkStackNode;typedef struct { LinkStackNode *top; int clen;} LinkStack;

2.2 创建

LinkStack *CreateLinkStack(){ LinkStack* ls=malloc(sizeof(LinkStack)); if(ls==NULL) { fprintf(stderr, \"CreateLinkStack malloc\\n\"); return NULL; } ls->top=NULL; ls->clen=0; return ls;}

2.3 入栈

int IsEmptyLinkStack(LinkStack *ls){ return ls->clen==0;}int PushLinkStack(LinkStack *ls,DATATYPE* data){ LinkStackNode* newnode=malloc(sizeof(LinkStackNode)); if(newnode==NULL) { fprintf(stderr, \"CreateLinkStack malloc\\n\"); return 1; } memcpy(&newnode->data, data, sizeof(DATATYPE)); newnode->next=NULL; if(IsEmptyLinkStack(ls)) { ls->top=newnode; }else { newnode->next=ls->top; ls->top=newnode; } ls->clen++; return 0;}

2.4 出栈

int PopLinkStack(LinkStack *ls){ LinkStackNode *tmp=ls->top; if(IsEmptyLinkStack(ls)) { return 1; } ls->top=ls->top->next; free(tmp); ls->clen--; return 0;}

2.5 获得栈顶元素

DATATYPE* GetTopLinkStack(LinkStack* ls)//获得栈顶元素{ if(IsEmptyLinkStack(ls)) { return NULL; } return &ls->top->data;}

2.6  销毁栈

int GetSizeLinkStack(LinkStack* ls){ return ls->clen;}int DestroyLinkStack(LinkStack *ls){ int size=GetSizeLinkStack(ls); for (int i=0;i<size;i++) { PopLinkStack(ls); } free(ls); return 0;}

3、队列概念

队列只允许在一段进行插入，儿在另一端进行删除操作的线性表，先进先出

允许插入的称队尾，允许删除的一端是队头

重要操作：入队和出队

head指向队首元素，tail指向队尾元素的下一个位置（即新元素插入的位置）。  

队列容量为 MAX_SIZE，但实际最多存储 MAX_SIZE - 1 个元素

4、队列

4.1 定义

typedef int DATATYPE; //通用数据类型int——DATATYPEtypedef struct queue {DATATYPE *ptr;int tlen;int head;int tail;}SeqQueue;

4.2 创建

SeqQueue *CreateSeqQueue(int len){ SeqQueue* sq=malloc(sizeof(SeqQueue)); if(sq==NULL) { fprintf(stderr,\"CreateSeqQueue malloc error\\n\"); return NULL; } sq->ptr=malloc(sizeof(DATATYPE)*len); if (sq->ptr==NULL) { fprintf(stderr,\"CreateSeqQueue malloc error\\n\"); return NULL; } sq->head=0; sq->tail=0; sq->tlen=len; return sq;}

4.3入队

int IsFullSeqQueue(SeqQueue *queue){ return (queue->tail+1)%queue->tlen==queue->head;}int EnterSeqQueue(SeqQueue *queue,DATATYPE *data){ if(IsFullSeqQueue(queue)) { printf(\"queue is full\\n\"); return 1; } memcpy(&queue->ptr[queue->tail], data, sizeof(DATATYPE)); queue->tail=(queue->tail+1)%queue->tlen;//? return 0;}

 2.4 出队

int IsEmptySeqQueue(SeqQueue *queue){ return queue->head==queue->tail;}int QuitSeqQueue(SeqQueue *queue){ if(IsEmptySeqQueue(queue)) { printf(\"queue is empty\\n\"); return 1; } queue->head=(queue->head+1)%queue->tlen; return 0;}

2.5 获得队头元素

DATATYPE* GetHeadSeqQueue(SeqQueue *queue){ if(IsEmptySeqQueue(queue)) { return NULL; } return &queue->ptr[queue->head];}

2.6 销毁队

int DestroySeqQueue(SeqQueue *queue){ free(queue->ptr); free(queue); return 0;}

四、树、二叉树

1、树

树：n（n>=0）个结点的有限集合。（n = 0 ,空树）

在任意一个非空树中，
1，有且仅有一个特定的根结点
2，当n>1 时，其余结点可分为m个互不相交的有限集合T1,T2,T3........Tn，其中每一个集合又是一个树，并且称谓子树。

结点拥有子树的个数称谓结点的度。度为0的结点称谓叶结点。度不为0，称谓分支结点。

树的度数是指，这棵树中，最大的结点的度数，称谓树的度数。
树的深度或高度，从根开始，根为第一层，根的孩子为第二层。

2、二叉树

n个结点的有限集合，集合要么为空树，要么由一个根结点和两棵互不相交，分别称谓根结点的左子树和右子树的二叉树组成。

特点
1，每个结点最多两个子树。
2，左子树和右子树是有顺序的，次序不能颠倒。
3，如果某个结点只有一个子树，也要区分左，右子树。

 特殊的二叉树
1，斜树，所有的结点都只有左子树，左斜树，所有结点都只有右子树，右树。
2，满二叉树，所有的分支结点都存在左右子树，并且叶子都在同一层上。
3，完全二叉树，对于一颗有n个结点的二叉树按层序编号，如果编号i（1<=i<=n）的结点于同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这可树为完全二叉树。

 特性
1、在二叉树的第i层上最多有2^(i-1)个结点 i>=1
2、深度为k的二叉树至多有2^k  -1 个结点 k>=1
3、任意一个二叉树T，如果其叶子结点的个数是n0,度数为2的结点数为n2， n0 = n2 +1
4、有n个结点的完全二叉树深度为(logn/log 2) +1;

广度遍历：

从上往下，从左往右

深度遍历：
前序，根左右，先访问根，然访问左，访问右。
中序，左根右，先从根开始（不是先访问根），从左开始访问，在访问根，在访问右结点。
后序，左右根，先从根开始（不是先访问根），先访问左，在访问右。在访问根。

3、代码

typedef char DATATYPE; //数据域typedef struct BiTNode { DATATYPE data; struct BiTNode *lchild,*rchild; //指针域}BiTNode;char dat[]=\"abd##eh###c#fi###\";int ind;//创建树void CreateTree(BiTNode ** root){ char c=dat[ind++]; if(\'#\'==c) { *root=NULL; }else { *root=malloc(sizeof(BiTNode)); if(*root==NULL) { printf(\"malloc error\\n\"); return ; } (*root)->data=c; CreateTree(&(*root)->lchild); CreateTree(&(*root)->rchild); } return;}//先序遍历void PreOrderTraverse(BiTNode*root){ if(root==NULL) { return; }else { printf(\"%c\",root->data); PreOrderTraverse(root->lchild); PreOrderTraverse(root->rchild); }}//中序遍历void InOrderTraverse(BiTNode* root){ if(root==NULL) { return; }else { PreOrderTraverse(root->lchild); printf(\"%c\",root->data); PreOrderTraverse(root->rchild); }}//后序遍历void PostOrderTraverse(BiTNode* root){ if(root==NULL) { return; }else { PreOrderTraverse(root->lchild); PreOrderTraverse(root->rchild); printf(\"%c\",root->data); }}//销毁树void DestroyBiTree(BiTNode*root){ if(root==NULL) { return; } DestroyBiTree(root->lchild); DestroyBiTree(root->rchild); free(root);}

五、哈希表、内核链表

1、散列表查找（哈希表）

1.1 概念

哈希是存储查找思想、主要体现在查找

本质是线性表的顺序存储方式（支持随机访问）希望快速查找若干数据

存储位置=f(关键字)，f()哈希函数

1.1 哈希函数构造方法

直接定址法、数据分析法、平方取中法、折叠法、除留余数法、随机数法

1.2 解决冲突（两个关键字不相等）的方法

开放定址（线性探测（+1，+2...）、二次探测(+1\\-1,+2\\-2...)、随机探测(加个随机数)）、再散列函数法、链地址法

1.3代码

typedef int DATATYPE;typedef struct{ DATATYPE* head; int tlen;}HXTABLE;HXTABLE* CreateHXTable(int n){ HXTABLE* hx=malloc(sizeof(HXTABLE)); if(hx==NULL) { fprintf(stderr,\"CreateHSTable malloc\"); return NULL; } hx->head=malloc(sizeof(DATATYPE)); if(hx->head==NULL) { fprintf(stderr,\"CreateHSTable malloc\"); return NULL; } hx->tlen=n; for(int i=0;ihead[i]=-1; } return hx;}int HXFun(HXTABLE* hx,DATATYPE* data){ return *data%hx->tlen;}int HX_Insert(HXTABLE* hx,DATATYPE* data){ int index=HXFun(hx, data); while (hx->head[index]!=-1) { printf(\"冲突 idx:%d num:%d\\n\",index, *data); index=(index+1)%hx->tlen; } hx->head[index]=*data; return 0;}int HX_Search(HXTABLE* hx,DATATYPE* data){ int index=HXFun(hx, data); int old_index=index; while (hx->head[index]!=*data) { index=(index+1)%hx->tlen; if(old_index==index) { return -1; } } return index; return 0;}int DestroyHX(HXTABLE* hx){ free(hx->head); free(hx); return 0;}DATATYPE *GetItemHXTable(HXTABLE* hx,int index){ if(indexhx->tlen-1) { return NULL; } return &hx->head[index];}

2、内核链表

1、数据域和指针域分离

2、双向循环链表

3、操作系统内部使用

重要的宏：containerof()获得结构：体指针；foreach()；list_add()；list_del()

附录

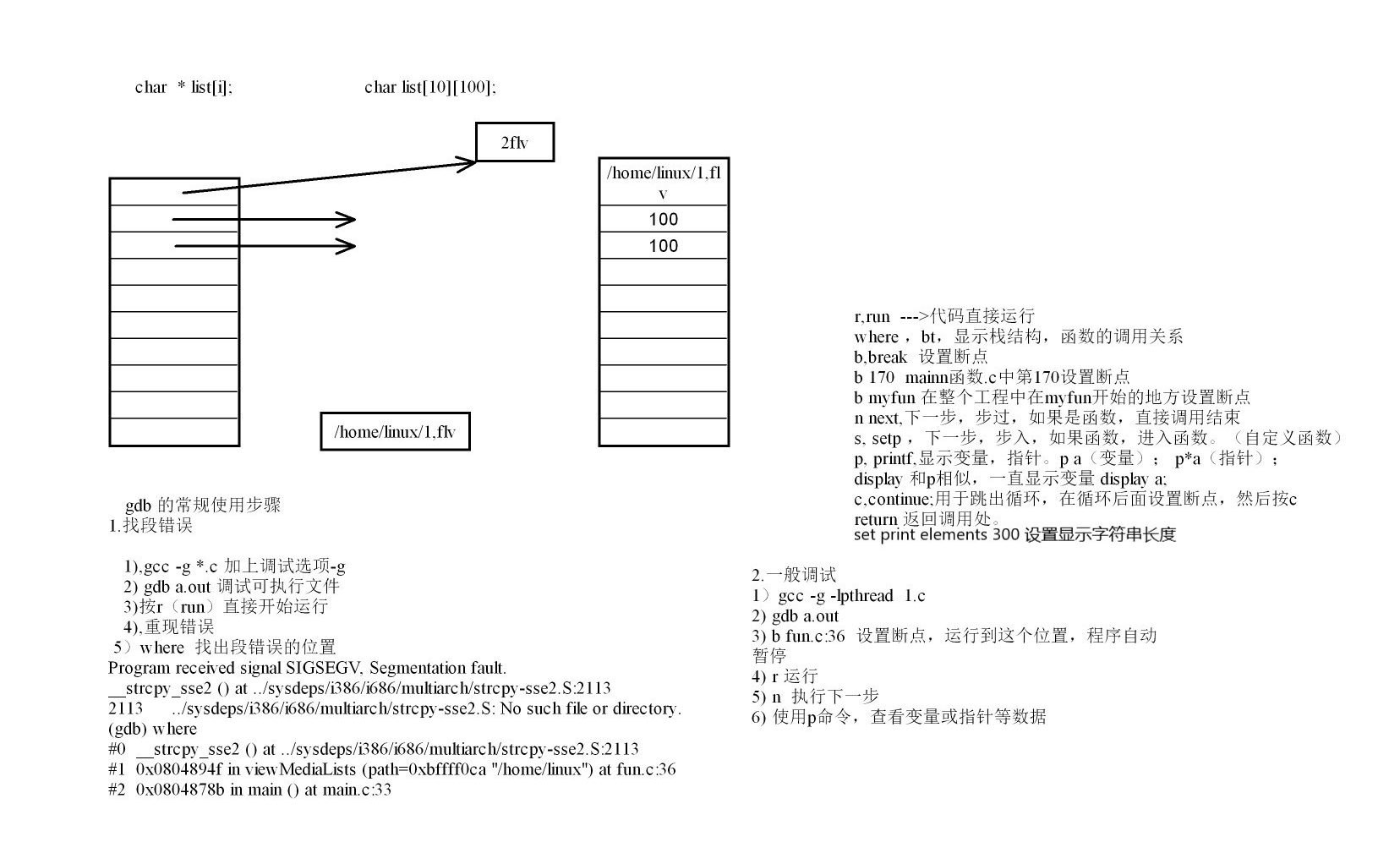
1、gdb

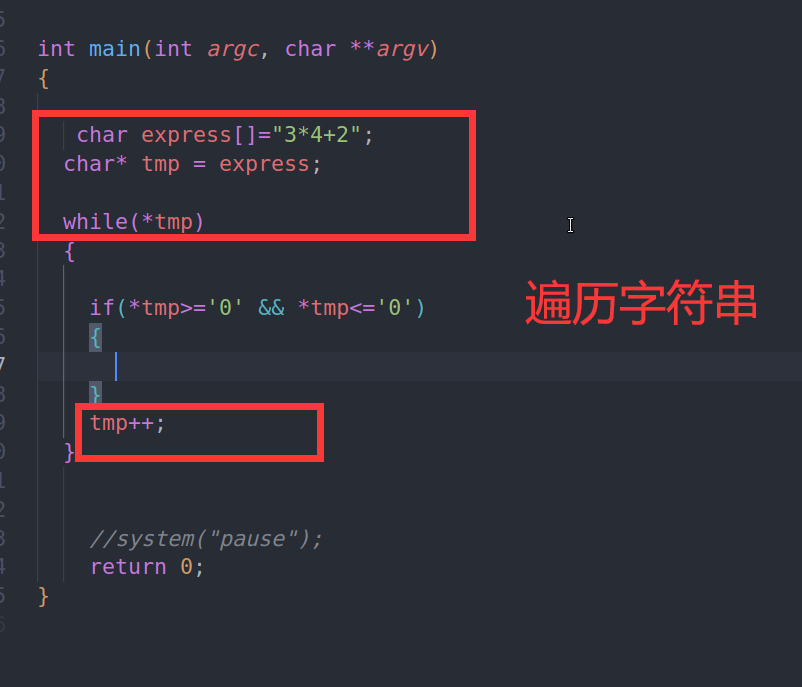
2、遍历 字符数组