图论——最近公共祖先_求解最近公共祖先的算法

方法1：向上标记法

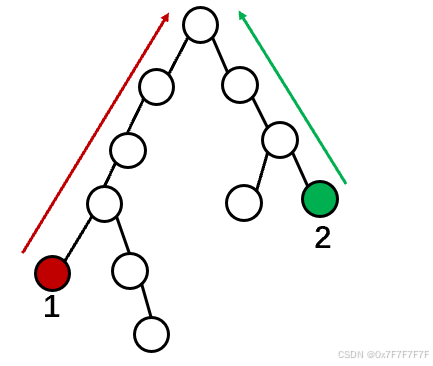
1.先从一号点往上走，走过的点都标记。
2.再从二号点往上走，走到的第一个带标记的点就是最近公共祖先。
时间复杂度:$O(n)$

方法2：倍增法

1.预处理：预处理出每个点向上走2k2^k2k步的节点的父亲是谁,用$f[i][j]$ 从$i$开始向上走2j2^j2j步所能走到的节点 $0<=j<=logn$。
$fa[i][j]==fa[fa[i][j-1]][j-1]$
同时预处理出每个点的深度
$depth[j]=depth[t]+1$
把$depth[root]$初始化为1；把$depth[0]$初始化为0，作为哨兵。
时间复杂度为$O(nlogn)$。
2.查询：
步骤1：让节点$a$和$b$走到同一深度下，假设$a$的深度更深，则从$a$跳到$b$，从$a$跳2k2^k2k步后的点的深度 $depth(f[a][k])>=depth(b)$时 就可以继续跳,$k$从$logn$到0枚举。
步骤2：让节点$a$和$b$在满足$fa[a][k]!=fa[b][k]$的条件下一起向上走，最后一定会停留在$lca$的下一层，最后$fa[a][0]$即是答案。
时间复杂度$O(logn)$

方法3：tarjan(离线做法)

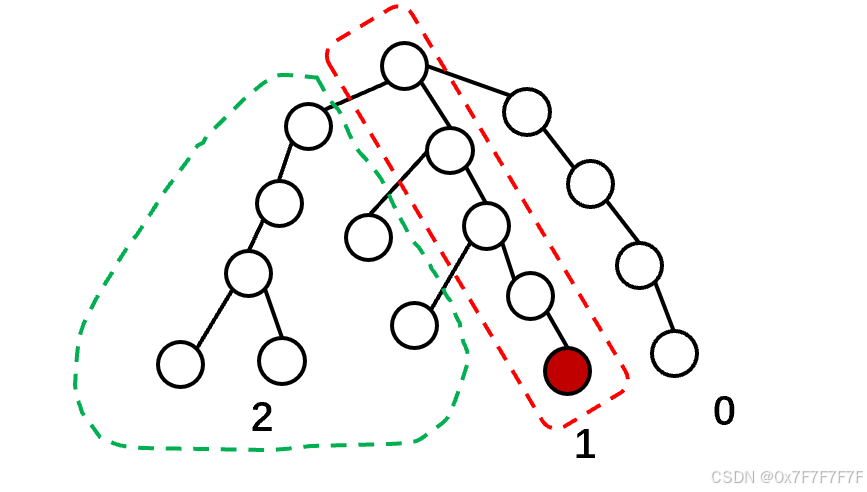
我们把所有的点分成三类：
2类节点为我们已经访问过并回溯过的
1类节点是我们正在访问的
0类节点是还没有访问到的

我们可以发现，2类节点和1类节点的$lca$一定在和这个2类节点相连的第一个1类节点上，所以我们在每一个节点回溯时，可以直接合并到它父节点的集合里，最后我们求1个1类节点和2类节点的$lca$时可以直接返回这个2类节点的集合编号。

我们提前存储每一次的查询，在我们搜索到某一个节点时取出和这个节点有关的所有查询，然后判断另一个节点是否是2类节点，如果是则可以直接返回他们俩的最近公共祖先。

我们对图进行了一次遍历，同时考虑了每一个查询，总共的时间复杂度是$O(n+m)$。

祖孙查询

给定一棵包含$n$个节点的有根无向树，节点编号互不相同，但不一定是$1\sim n$。

有$m$个询问，每个询问给出了一对节点的编号$x$和$y$，询问$x$与$ y$的祖孙关系。

输入格式
输入第一行包括一个整数 表示节点个数；

接下来$n$行每行一对整数$a$和$b$，表示$a$和$b$之间有一条无向边。如果$b$是$-1$，那么$a$就是树的根；
第$n+2$行是一个整数$m$表示询问个数；
接下来$m$行，每行两个不同的正整数$x$和$y$，表示一个询问。

输出格式
对于每一个询问，若$x$是 $y$的祖先则输出 $1$，若 $y$ 是 $x$ 的祖先则输出 $2$，否则输出 $0$。

数据范围
1≤n,m≤4×1041≤n,m≤4×10^41≤n,m≤4×104,$1\le$每个节点的编号≤4×104≤4×10^4≤4×104

输入样例：

10234 -112 23413 23414 23415 23416 23417 23418 23419 234233 195234 233233 12233 13233 15233 19

输出样例：

10002

倍增求lca模板题。

#include #include using namespace std;const int N = 40010, M = 2 * N;int depth[N], fa[N][20];int h[N], e[M], ne[M], w[M], tot;int q[N];int n, m;int root = 0;void add(int a, int b){ e[tot] = b, ne[tot] = h[a], h[a] = tot ++ ;}void bfs(){ memset(depth, 0x3f, sizeof depth); depth[root] = 1, depth[0] = 0; int hh = 0, tt = 0; q[0] = root; while (hh <= tt) { int t = q[hh ++ ]; for (int i = h[t]; ~i; i = ne[i]) { int j = e[i]; if (depth[j] > depth[t] + 1) { depth[j] = depth[t] + 1; fa[j][0] = t; q[++ tt] = j; for (int k = 1; k <= 15; k ++ )  fa[j][k] = fa[fa[j][k - 1]][k - 1]; } } }}int lca(int a, int b){ if (depth[a] < depth[b]) swap(a, b); for (int k = 15; k >= 0; k -- ) { if (depth[fa[a][k]] >= depth[b]) a = fa[a][k]; } if (a == b) return b; for (int k = 15; k >= 0; k -- ) { if (fa[a][k] != fa[b][k]) { a = fa[a][k], b = fa[a][k]; } } return fa[a][0];}int main(){ cin >> n; memset(h, -1, sizeof h); for (int i = 1; i <= n; i ++ ) { int a, b; cin >> a >> b; if (b == -1) root = a; else add(a, b), add(b, a); } bfs(); cin >> m; while (m -- ) { int a, b; cin >> a >> b; int p = lca(a, b); if (p == a) puts(\"1\"); else if (p == b) puts(\"2\"); else puts(\"0\"); } return 0;}

距离

给出$n$个点的一棵树，多次询问两点之间的最短距离。

注意：

边是无向的。所有节点的编号是 $1,2,\dots ,n$。
输入格式
第一行为两个整数$n$和$m$。$n$表示点数，$m$表示询问次数；

下来 $n-1$ 行，每行三个整数$x,y,k$，表示点 $x$ 和点 $y$ 之间存在一条边长度为 $k$；

再接下来 $m$ 行，每行两个整数 $x,y$，表示询问点 $x$ 到点 $y$ 的最短距离。

树中结点编号从 $1$ 到 $n$。

输出格式共 $m$ 行，对于每次询问，输出一行询问结果。

数据范围
2≤n≤104,2≤n≤10^4,2≤n≤104,
1≤m≤2×104,1≤m≤2×10^4,1≤m≤2×104,
$0<k\le 100,$
$1\le x,y\le n$

输入样例1：

2 2 1 2 100 1 2 2 1

输出样例1：

100100

输入样例2：

3 21 2 103 1 151 23 2

输出样例2：

1025

想要求树上两个点$a,b$的距离，相当于找到他们的$lca$，然后两者到$lca$的距离之和，也相当于求$a$到根节点的距离，$b$到根节点的距离，$lca$到根节点的距离，然后$depth[a]+depth[b]-2\ast depth[lca]$，考虑使用$tarjan$离线做法。

#include #include #include using namespace std;const int N = 10010, M = N * 2, K = 20010;typedef pair<int,int> PII;vector<PII> query[N];int h[N], w[M], e[M], ne[M], tot;int dist[N];int st[N];int p[N];int res[K];int n, m;void add(int a, int b, int c){ e[tot] = b, ne[tot] = h[a], w[tot] = c, h[a] = tot ++ ;}int find(int x){ return x == p[x] ? x : p[x] = find(p[x]);}void dfs(int u, int fa){ for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if (j == fa) continue; dist[j] = dist[u] + w[i]; dfs(j, u); } return ; }void tarjan(int u, int fa){ st[u] = 1; for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if (j != fa) { tarjan(j, u); p[j] = u; } } for (auto i : query[u]) { int y = i.first, id = i.second; if (st[y] == 2) { int anc = find(y); res[id] = dist[y] + dist[u] - 2 * dist[anc]; } } st[u] = 2; return ;}int main(){ cin >> n >> m; memset(h, -1, sizeof h); for (int i = 1; i < n; i ++ ) { int x, y, k; cin >> x >> y >> k; add(x, y, k), add(y, x, k); } for (int i = 1; i <= m; i ++ ) { int x, y; cin >> x >> y; query[x].push_back({y, i}); query[y].push_back({x, i}); } for (int i = 1; i <= n; i ++ ) p[i] = i; dfs(1, 0); tarjan(1, 0); for (int i = 1; i <= m; i ++ ) cout << res[i] << endl; return 0;}

[BJWC2010] 严格次小生成树

小 C 最近学了很多最小生成树的算法，Prim 算法、Kruskal 算法、消圈算法等等。正当小 C 洋洋得意之时，小 P 又来泼小 C 冷水了。小 P 说，让小 C 求出一个无向图的次小生成树，而且这个次小生成树还得是严格次小的，也就是说：如果最小生成树选择的边集是 EME_MEM​，严格次小生成树选择的边集是 ESE_SES​，那么需要满足：($value(e)$ 表示边 $e$ 的权值) ∑e∈EMvalue(e)<∑e∈ESvalue(e)\\sum_{e \\in E_M}value(e)<\\sum_{e \\in E_S}value(e)∑e∈EM​​value(e)<∑e∈ES​​value(e)。

这下小 C 蒙了，他找到了你，希望你帮他解决这个问题。

输入格式

第一行包含两个整数 $N$ 和 $M$，表示无向图的点数与边数。

接下来 $M$ 行，每行 $3$ 个数 $x,y,z$ 表示，点 $x$ 和点 $y$ 之间有一条边，边的权值为 $z$。

输出格式

包含一行，仅一个数，表示严格次小生成树的边权和。

样例 #1

样例输入 #1

5 61 2 1 1 3 2 2 4 3 3 5 4 3 4 3 4 5 6

样例输出 #1

11

提示

数据中无向图不保证无自环。

对于 $50\%$ 的数据， $N\le 2000$，$M\le 3000$。

对于 $80\%$ 的数据， N≤5×104N\\le 5\\times 10^4N≤5×104，M≤105M\\le 10^5M≤105。

对于 $100\%$ 的数据， N≤105N\\le 10^5N≤105，M≤3×105M\\le 3\\times10^5M≤3×105，边权 ∈[0,109]\\in [0,10^9]∈[0,109]，数据保证必定存在严格次小生成树。

考虑加入一条非树边$(a,b,w)$显然用它替换掉树上$a\to b$路径中的某一条边,路径上的最大值为$dist1$，严格次大值为$dist2$,如果$w>dist1$,那么可以用这条边替换权值为$dist1$的这条边，如果$w\le dist1\&\&w>dist2$，那么可以用这条边替换权值为$dist2$的这条边。本题的关键在于如何快速的找到一条路径上的$dist1$和$dist2$,解决办法如下：

定义数组$d1[N][17]$和数组$d2[N][17]$，$d1[i][j]$表示树节点$i$节点跳2j2^j2j且不超过跟这段范围内的权值最大值,$d2[i][j]$表示树节点$i$节点跳2j2^j2j且不超过跟这段范围内的权值严格次大值。$anc=fa[i][j-1]$,在$d1[i][j-1],d1[anc][j-1],d1[i][j-1],d1[anc][j-1]$中，$d1[i][j]$为里面最大值，$d2[i][j]$为里面的严格次大值。
对于一条非树边$(a,b,w)$,我们在倍增找到$a,b$的$lca$的过程中，如果可以往上走2j2^j2j,那么我们就维护一个数组$distance$存储下来$d1[i][j]$还有$d2[i][j]$，最后在所以存储下来的值中，最大值就是$dist1$,严格次小值就是$dist2$。

本题总体解决思路如下：
1走一遍$kruskal$找到最小生成树，同时求出边权和$sum$。
2.用最小生成树的边来进行建图。
3.在图中走一遍$bfs$完成对$fa,d1,d2$数组的预处理。
4.枚举每一条非树边$(a,b,w)$，用倍增法找到$a,b$的$lca$,同时返回$w-dist$的结果。

#include #include #include using namespace std;typedef long long ll;const int N = 100010, M = 300010;const int INF = 0x3f3f3f3f;int p[N];struct Edge{ int a, b, w; bool flag; bool operator< (const Edge&t) const{ return w < t.w; }}edge[M];int fa[N][20], d1[N][20], d2[N][20];int q[N];int dist[N];int h[N], e[M], ne[M], w[M], tot;int n, m;void add(int a, int b, int c){ e[tot] = b, ne[tot] = h[a], w[tot] = c, h[a] = tot ++ ;}int find(int x){ return p[x] == x ? x : p[x] = find(p[x]);}ll kruskal(){ ll res = 0; for (int i = 1; i <= n; i ++ ) p[i] = i; sort(edge + 1, edge + m + 1); for (int i = 1; i <= m; i ++ ) { int a = find(edge[i].a), b = find(edge[i].b), w = edge[i].w; if (a != b) { p[a] = b; res += w; edge[i].flag = 1; } } return res;}void bfs(){ memset(dist, 0x3f, sizeof dist); dist[1] = 1, dist[0] = 0; int hh = 0, tt = 0; q[0] = 1; while (hh <= tt) { int t = q[hh ++ ]; for (int i = h[t]; ~i; i = ne[i]) { int j = e[i]; if (dist[j] > dist[t] + 1) { dist[j] = dist[t] + 1; fa[j][0] = t; d1[j][0] = w[i], d2[j][0] = -INF; q[++ tt] = j; for (int k = 1; k <= 16; k ++ ) {  int anc = fa[j][k - 1];  fa[j][k] = fa[anc][k - 1];  d1[j][k] = d2[j][k] = -INF;  int distance[4] = {d1[j][k - 1], d2[j][k - 1], d1[anc][k - 1], d2[anc][k - 1]};  for (int u = 0; u < 4; u ++ )  { int d = distance[u]; if (d > d1[j][k]) d2[j][k] = d1[j][k], d1[j][k] = d; else if (d < d1[j][k] && d > d2[j][k]) d2[j][k] = d;  } } } } }}int lca(int a, int b, int w){ static int dis[N * 2]; int cnt = 0; if (dist[a] < dist[b]) swap(a, b); for (int k = 16; k >= 0; k -- ) { if (dist[fa[a][k]] >= dist[b]) { dis[cnt ++ ] = d1[a][k]; dis[cnt ++ ] = d2[a][k]; a = fa[a][k]; } } if (a != b) { for (int k = 16; k >= 0; k -- ) { if (fa[a][k] != fa[b][k]) { dis[cnt ++ ] = d1[a][k]; dis[cnt ++ ] = d2[a][k]; dis[cnt ++ ] = d1[b][k]; dis[cnt ++ ] = d2[b][k]; a = fa[a][k], b = fa[b][k]; } } dis[cnt ++ ] = d1[a][0]; dis[cnt ++ ] = d1[b][0]; } int dist1 = -INF, dist2 = -INF; for (int i = 0; i < cnt; i ++ ) { if (dist1 < dis[i]) dist2 = dist1, dist1 = dis[i]; else if (dis[i] < dist1 && dis[i] > dist2) dist2 = dis[i]; } if (w > dist1) return w - dist1; if (w > dist2) return w - dist2; return INF;}int main(){ cin >> n >> m; for (int i = 1; i <= m; i ++ ) { int a, b, w; cin >> a >> b >> w; edge[i] = {a, b, w}; } ll sum = kruskal(); memset(h, -1, sizeof h); for (int i = 1; i <= m; i ++ ) { int a = edge[i].a, b = edge[i].b, w = edge[i].w; if (edge[i].flag) add(a, b, w), add(b, a, w); } bfs(); ll res = 1e18; for (int i = 1; i <= m; i ++ ) { int a = edge[i].a, b = edge[i].b, w = edge[i].w; if (!edge[i].flag) res = min(res, sum + lca(a, b, w)); } cout << res; return 0;}

闇の連鎖

题目描述

传说中的暗之连锁被人们称为 Dark。

Dark 是人类内心的黑暗的产物，古今中外的勇者们都试图打倒它。

经过研究，你发现 Dark 呈现无向图的结构，图中有 $N$ 个节点和两类边，一类边被称为主要边，而另一类被称为附加边。

Dark 有 $N-1$ 条主要边，并且 Dark 的任意两个节点之间都存在一条只由主要边构成的路径。

另外，Dark 还有 $M$ 条附加边。

你的任务是把 Dark 斩为不连通的两部分。

一开始 Dark 的附加边都处于无敌状态，你只能选择一条主要边切断。

一旦你切断了一条主要边，Dark 就会进入防御模式，主要边会变为无敌的而附加边可以被切断。

但是你的能力只能再切断 Dark 的一条附加边。

现在你想要知道，一共有多少种方案可以击败 Dark。

注意，就算你第一步切断主要边之后就已经把 Dark 斩为两截，你也需要切断一条附加边才算击败了 Dark。

输入格式

第一行包含两个整数 $N$ 和 $M$。

之后 $N-1$ 行，每行包括两个整数 $A$ 和 $B$，表示 $A$ 和 $B$ 之间有一条主要边。

之后 $M$ 行以同样的格式给出附加边。

输出格式

输出一个整数表示答案。

样例 #1

样例输入 #1

4 11 22 31 43 4

样例输出 #1

3

提示

数据保证，$1\le N\le 100000$，$1\le M\le 200000$，数据保证答案不超过 231−12^{31}-1231−1。

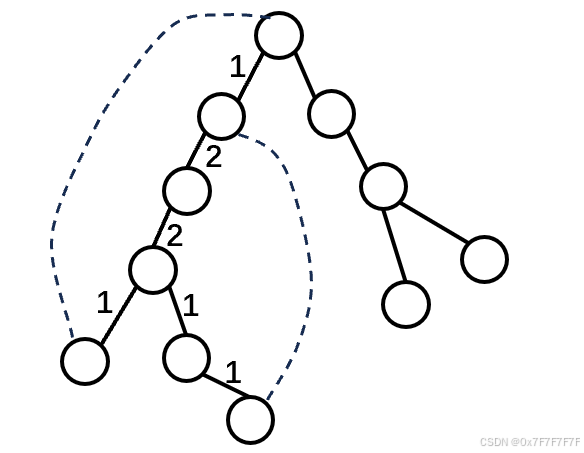
在没有附加边的情况下，我们发现这是一颗树，那么再添加条附加边$(x，y)$后，会造成$(x，y)$之间产生一个环
如果我们第一步截断了$(x，y)$之间的一条路，那么我们第二次只能截掉$(x，y)$之间的附加边，才能使其不连通；
我们将每条附加边$(x，y)$称为将$(x，y)$之间的路径覆盖了一遍；
因此我们只需要统计出每条主要边被覆盖了几次即可；
对于只被覆盖一次的边，第二次我们只能切断$(x，y)$边，方法唯一；
如果我们第一步切断了被覆盖0次的边，那么我们已经将其分为两部分，那么第二部只需要在$m$条附加边中任选一条即可，如果第一步截到被覆盖超过两次的边，将无法将其分为两部分；
运用乘法原理，我们累加答案；
我们可以使用树上差分标记我们的边$(x，y)$被覆盖了几次。

#include #include using namespace std;const int N = 100010, M = 200010;int h[N], e[M], ne[M], tot;int dist[N];int fa[N][20];int d[N];int n, m;int ans = 0;int q[N];void add(int a, int b){ e[tot] = b, ne[tot] = h[a], h[a] = tot ++ ;}void bfs(){ memset(dist, 0x3f, sizeof dist); q[0] = 1; dist[1] = 1, dist[0] = 0; int hh = 0, tt = 0; while (hh <= tt) { int t = q[hh ++ ]; for (int i = h[t]; ~i; i = ne[i]) { int j = e[i]; if (dist[j] > dist[t] + 1) { dist[j] = dist[t] + 1; fa[j][0] = t; q[++ tt] = j; for (int k = 1; k <= 16; k ++ )  fa[j][k] = fa[fa[j][k - 1]][k - 1]; } } }}int lca(int a, int b){ if (dist[a] < dist[b]) swap(a, b); for (int i = 16; i >= 0; i -- ) if (dist[fa[a][i]] >= dist[b]) a = fa[a][i]; if (a == b) return a; for (int i = 16; i >= 0; i -- ) { if (fa[a][i] != fa[b][i]) { a = fa[a][i]; b = fa[b][i]; } } return fa[a][0];}int dfs(int u, int p){ int res = d[u]; for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if (j == p) continue; int s = dfs(j, u); if (s == 0) ans += m; else if (s == 1) ans += 1; res += s; } return res;}int main(){ cin >> n >> m; memset(h, -1, sizeof h); for (int i = 1; i < n; i ++ ) { int a, b; cin >> a >> b; add(a, b), add(b, a); } bfs(); for (int i = 1; i <= m; i ++ ) { int a, b; cin >> a >> b; int p = lca(a, b); d[a] ++ ,d[b] ++ , d[p] -= 2; } dfs(1, 0); cout << ans;}