多智能体强化学习入门：从基础到 IPPO 算法—强化学习(20)

技术文档

1、什么是多智能体强化学习？

2、多智能体强化学习的问题建模

2.1、核心要素

2.2、核心挑战

2.3、目标：优化联合策略

3、多智能体强化学习的基本求解范式

3.1、完全中心化（Centralized）

3.1.1、核心思想：

3.1.2、具体做法：

3.1.3、优点：

3.1.4、缺点：

3.2、完全去中心化（Decentralized）

3.2.1、核心思想：

3.2.2、具体做法：

3.2.3、优点：

3.2.4、缺点：

3.3、为什么需要 “中间方案”？

4、IPPO：多智能体版的 PPO 算法

4.1、先回顾 PPO 的核心思想

4.2、 IPPO 如何适配多智能体场景？

4.2.1、步骤拆解：

4.3、 IPPO 的优势

5、完整代码

6、实验结果

1、什么是多智能体强化学习？

多智能体强化学习（Multi-Agent Reinforcement Learning，MARL）是研究多个智能体在同一环境中交互、协作或竞争，并通过学习优化各自策略的领域。

和单智能体强化学习（如 AlphaGo 独自学习围棋）不同，MARL 的核心是智能体之间的相互影响：比如自动驾驶中多辆车的避障（协作）、团队游戏中 5v5 的对抗（竞争 + 协作）、无人机群的协同搜救（纯协作）。

举个例子：在《王者荣耀》这样的 5v5 游戏中，每个英雄都是一个智能体，需要学习 “何时配合队友抓人”“如何分工推塔”—— 这就是典型的多智能体强化学习场景。

2、多智能体强化学习的问题建模

要理解 MARL，先明确其核心要素和挑战。我们用符号和通俗例子结合的方式说明：

2.1、核心要素

智能体（Agents）：多个独立决策的个体，记为 $i = 1, 2, ..., N$ （比如 5 个游戏玩家）。
状态（State）：环境的全局信息，记为 $s \\in \\mathcal{S}$ （比如游戏中所有英雄的位置、血量）。
局部观测（Observation）：智能体 i 能看到的部分信息，记为 $o_i \\in \\mathcal{O}_i$ （比如你在游戏中只能看到自己视野内的敌人）。
动作（Action）：智能体 i 选择的行为，记为 $a_i \\in \\mathcal{A}_i$ （比如 “释放技能”“移动”）。所有智能体的动作组成联合动作 $\\mathbf{a} = (a_1, a_2, ..., a_N)$ 。
奖励（Reward）：
- 个体奖励 $r_i$ ：智能体 i 获得的局部反馈（比如你击杀敌人得到的金币）；
- 全局奖励 r：整个团队的反馈（比如团队推掉水晶的胜利奖励）。
策略（Policy）：智能体 i 根据观测选择动作的规则，记为 $\\pi_i(a_i | o_i)$ （比如 “看到敌人残血就追击”）。

2.2、核心挑战

多智能体的复杂之处，源于 “智能体之间的相互影响”，带来了单智能体没有的问题：

环境非平稳性：对单个智能体来说，其他智能体的策略在学习过程中会不断变化，相当于 “环境在动态改变”。比如你刚适应队友的打法，队友又学会了新策略，导致你之前的经验失效。
信用分配难题：当团队获得全局奖励（比如 “赢了比赛”），很难判断每个智能体的贡献（是辅助的控制关键，还是 ADC 的输出关键？），导致个体策略难以优化。
通信与协作：智能体需要通过动作间接 “通信”（比如游戏中 “信号 ping 敌方”），如何学习高效的协作模式是难点。

2.3、目标：优化联合策略

3、多智能体强化学习的基本求解范式

针对多智能体的协作与决策，有两种极端的求解思路：完全中心化和完全去中心化。

3.1、完全中心化（Centralized）

3.1.1、核心思想：

有一个 “中央控制器”，掌握所有智能体的状态、动作和全局奖励，统一优化所有智能体的策略。

3.1.2、具体做法：

中央控制器拥有全局视角：知道所有智能体的观测 $o_1, ..., o_N$ 和环境状态 s；
输出联合动作：直接决定每个智能体该做什么（比如教练在场边指挥每个队员的跑位）；
优化目标：基于全局奖励 r 调整联合策略，让团队整体收益最大。

3.1.3、优点：

能直接优化全局目标，协作效率高（比如无人机群在中央控制下精准避障）。

3.1.4、缺点：

计算量爆炸：当智能体数量 N 增加（比如 100 个无人机），联合动作空间 $\\mathcal{A}_1 \\times ... \\times \\mathcal{A}_N$ 太大，无法处理；
灵活性差：中央控制器故障会导致整个系统瘫痪，且智能体缺乏独立决策能力（比如教练不在，队员不会打了）。

3.2、完全去中心化（Decentralized）

3.2.1、核心思想：

每个智能体独立学习，只根据自己的局部观测和个体奖励决策，完全不知道其他智能体的信息。

3.2.2、具体做法：

每个智能体 i 只使用自己的观测 $o_i$ 和奖励 $r_i$ ；
独立优化自身策略 $\\pi_i$ ，比如用单智能体的 PPO、Q-learning 等算法（比如游戏中每个玩家只靠自己的经验摸索打法）。

3.2.3、优点：

计算量小：每个智能体的策略独立优化，不受其他智能体数量影响；
鲁棒性强：单个智能体故障不影响整体（比如一个无人机没电，其他仍能工作）。

3.2.4、缺点：

协作困难：智能体不知道队友的意图，容易出现 “各自为战”（比如游戏中队友同时抢一个 buff）；
难以利用全局奖励：个体看不到团队整体收益，可能 “捡芝麻丢西瓜”（比如为了个人击杀放弃推塔）。

3.3、为什么需要 “中间方案”？

完全中心化和去中心化都有明显缺陷。实际中常用 “去中心化执行，中心化评估”（Decentralized Execution, Centralized Critic，DECC）：

执行时：每个智能体独立决策（去中心化，灵活高效）；
评估时：有一个全局 “评委”（Centralized Critic），基于全局信息判断当前联合动作的好坏（中心化，解决信用分配问题）。

IPPO 算法就是这种中间方案的典型代表。

4、IPPO：多智能体版的 PPO 算法

IPPO（Independent PPO）是基于单智能体 PPO 扩展的多智能体算法，核心是 “让每个智能体独立用 PPO 学习，但用全局信息辅助评估”，实现高效协作。

4.1、先回顾 PPO 的核心思想

单智能体 PPO 是通过 “信任域优化” 稳定训练的算法：每次更新策略时，限制新策略与旧策略的差异（用 “剪辑” 技巧），避免更新幅度过大导致训练崩溃。

核心公式（剪辑损失）： $\\mathcal{L}^{\\text{CLIP}}(\\theta) = \\mathbb{E} \\left[ \\min \\left( \\frac{\\pi_\\theta(a|s)}{\\pi_{\\theta_{\\text{old}}}(a|s)} A(s,a), \\text{clip}\\left( \\frac{\\pi_\\theta(a|s)}{\\pi_{\\theta_{\\text{old}}}(a|s)}, 1-\\epsilon, 1+\\epsilon \\right) A(s,a) \\right) \\right]$

其中 A(s,a) 是优势函数（衡量动作的好坏）， $\\epsilon$ 是剪辑系数（通常取 0.2）。

4.2、 IPPO 如何适配多智能体场景？

IPPO 的核心是 **“每个智能体有独立的 PPO 策略，但共享一个集中式 Critic 评估全局优势”**。

4.2.1、步骤拆解：

步骤 1：去中心化执行 每个智能体 i 基于自己的观测 $o_i$ ，用独立的策略网络 $\\pi_i(a_i | o_i)$ 选择动作（比如游戏中每个英雄自己决定技能释放）。
步骤 2：中心化评估 有一个全局 Critic 网络，输入所有智能体的观测和动作（即联合观测 $\\mathbf{o} = (o_1, ..., o_N)$ 和联合动作 $\\mathbf{a} = (a_1, ..., a_N)$ ），输出全局优势函数 $A(\\mathbf{o}, \\mathbf{a})$ —— 衡量当前联合动作对团队整体的价值（比如 “这波团战的操作是赚还是亏”）。
步骤 3：用全局优势更新个体策略 每个智能体 i 的策略损失参考 PPO 的剪辑公式，但用全局优势 A 替代单智能体的优势： $\\mathcal{L}_i(\\theta_i) = \\mathbb{E} \\left[ \\min \\left( \\frac{\\pi_i(a_i | o_i)}{\\pi_{i,\\text{old}}(a_i | o_i)} A(\\mathbf{o}, \\mathbf{a}), \\text{clip}(...) A(\\mathbf{o}, \\mathbf{a}) \\right) \\right]$ 这样，每个智能体虽然独立决策，但能通过全局优势知道 “自己的动作对团队的贡献”，从而优化策略。
步骤 4：重复迭代 智能体不断与环境交互，收集联合观测、动作和全局奖励，更新 Critic（评估）和各自的策略（决策），直到策略收敛。

4.3、 IPPO 的优势

解决信用分配问题：通过全局 Critic，每个智能体能知道自己的动作在团队中的价值（比如 “我这波控制帮队友拿到了击杀，是有贡献的”）；
训练稳定：继承 PPO 的剪辑机制，避免多智能体环境中策略突变导致的训练震荡；
灵活性高：去中心化执行让智能体可独立适应环境变化（比如队友策略变了，自己也能调整）。

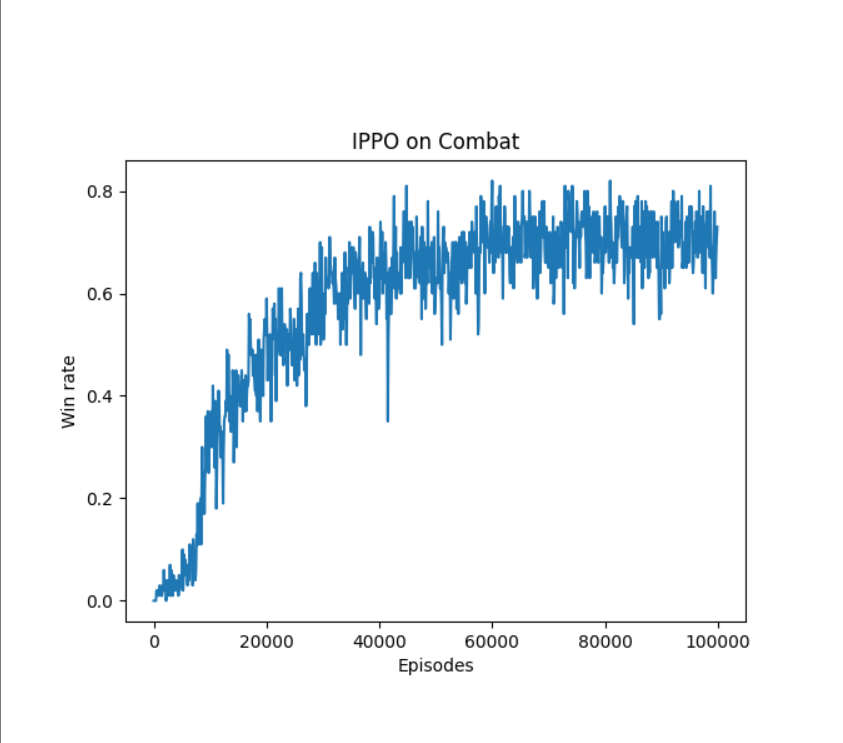
5、完整代码

import torchimport torch.nn.functional as Fimport numpy as npimport rl_utils # 自定义强化学习工具库，包含优势函数计算等功能from tqdm import tqdm # 用于显示训练进度条import matplotlib.pyplot as plt # 用于绘制胜率曲线from ma_gym.envs.combat.combat import Combat # 导入多智能体战斗环境class PolicyNet(torch.nn.Module): \"\"\"策略网络，用于输出动作概率分布\"\"\" def __init__(self, state_dim, hidden_dim, action_dim): super(PolicyNet, self).__init__() self.fc1 = torch.nn.Linear(state_dim, hidden_dim) # 第一层全连接 self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim) # 第二层全连接 self.fc3 = torch.nn.Linear(hidden_dim, action_dim) # 输出层，维度为动作空间大小 def forward(self, x): x = F.relu(self.fc2(F.relu(self.fc1(x)))) # 两层ReLU激活的非线性变换 return F.softmax(self.fc3(x), dim=1) # 将输出转换为概率分布class ValueNet(torch.nn.Module): \"\"\"价值网络，用于评估状态价值\"\"\" def __init__(self, state_dim, hidden_dim): super(ValueNet, self).__init__() self.fc1 = torch.nn.Linear(state_dim, hidden_dim) # 第一层全连接 self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim) # 第二层全连接 self.fc3 = torch.nn.Linear(hidden_dim, 1) # 输出层，输出单个状态价值 def forward(self, x): x = F.relu(self.fc2(F.relu(self.fc1(x)))) # 两层ReLU激活的非线性变换 return self.fc3(x) # 返回状态价值class PPO: \'\'\' PPO算法,采用截断方式 \'\'\' def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr,  lmbda, eps, gamma, device): self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device) # 策略网络(演员) self.critic = ValueNet(state_dim, hidden_dim).to(device) # 价值网络(评论家) self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr) # 演员优化器 self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr) # 评论家优化器 self.gamma = gamma # 折扣因子，控制未来奖励的重要性 self.lmbda = lmbda # GAE(广义优势估计)的参数 self.eps = eps # PPO中截断范围的参数，防止策略更新过大 self.device = device # 运行设备(CPU或GPU) def take_action(self, state): \"\"\"根据当前状态选择动作\"\"\" state = torch.tensor([state], dtype=torch.float).to(self.device) # 将状态转换为张量 probs = self.actor(state) # 获取动作概率分布 action_dist = torch.distributions.Categorical(probs) # 创建分类分布 action = action_dist.sample() # 从分布中采样动作 return action.item() # 返回动作的标量值 def update(self, transition_dict): \"\"\"更新策略网络和价值网络\"\"\" # 从字典中提取各元素并转换为张量 states = torch.tensor(transition_dict[\'states\'], dtype=torch.float).to(self.device) actions = torch.tensor(transition_dict[\'actions\']).view(-1, 1).to(self.device) rewards = torch.tensor(transition_dict[\'rewards\'], dtype=torch.float).view(-1, 1).to(self.device) next_states = torch.tensor(transition_dict[\'next_states\'], dtype=torch.float).to(self.device) dones = torch.tensor(transition_dict[\'dones\'], dtype=torch.float).view(-1, 1).to(self.device) # 计算TD目标(贝尔曼目标) td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones) # 计算TD误差 td_delta = td_target - self.critic(states) # 计算优势函数(使用GAE方法) advantage = rl_utils.compute_advantage(self.gamma, self.lmbda, td_delta.cpu()).to(self.device) # 计算旧策略下动作的对数概率(用于重要性采样) old_log_probs = torch.log(self.actor(states).gather(1, actions)).detach() # 计算新策略下动作的对数概率 log_probs = torch.log(self.actor(states).gather(1, actions)) # 计算新旧策略的概率比 ratio = torch.exp(log_probs - old_log_probs) # PPO-Clip损失的两部分 surr1 = ratio * advantage # 未截断的目标 surr2 = torch.clamp(ratio, 1 - self.eps, 1 + self.eps) * advantage # 截断后的目标 # 演员损失(取两部分的最小值，加负号转为最大化问题) actor_loss = torch.mean(-torch.min(surr1, surr2)) # 评论家损失(均方误差) critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach())) # 反向传播和优化 self.actor_optimizer.zero_grad() self.critic_optimizer.zero_grad() actor_loss.backward() critic_loss.backward() self.actor_optimizer.step() self.critic_optimizer.step()if __name__ == \'__main__\': # 超参数设置 actor_lr = 3e-4 # 演员网络学习率 critic_lr = 1e-3 # 评论家网络学习率 num_episodes = 100000 # 总训练回合数 hidden_dim = 64 # 隐藏层维度 gamma = 0.99 # 折扣因子 lmbda = 0.97 # GAE参数 eps = 0.2 # PPO截断参数 device = torch.device(\"cuda\") if torch.cuda.is_available() else torch.device(\"cpu\") # 运行设备 team_size = 2 # 每队智能体数量 grid_size = (15, 15) # 网格世界大小 # 创建Combat环境，双方各有2个智能体 env = Combat(grid_shape=grid_size, n_agents=team_size, n_opponents=team_size) # 获取状态空间和动作空间维度 state_dim = env.observation_space[0].shape[0] action_dim = env.action_space[0].n # 创建PPO智能体(两个智能体共享同一个策略，即参数共享) agent = PPO(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, lmbda, eps, gamma, device) win_list = [] # 存储每回合的胜负结果 # 分阶段训练，每个阶段显示进度条 for i in range(10): with tqdm(total=int(num_episodes / 10), desc=\'Iteration %d\' % i) as pbar: for i_episode in range(int(num_episodes / 10)): # 为两个智能体分别创建经验字典 transition_dict_1 = {  \'states\': [],  \'actions\': [],  \'next_states\': [],  \'rewards\': [],  \'dones\': [] } transition_dict_2 = {  \'states\': [],  \'actions\': [],  \'next_states\': [],  \'rewards\': [],  \'dones\': [] } s = env.reset() # 重置环境，获取初始状态 terminal = False # 回合终止标志 # 与环境交互直到回合结束 while not terminal:  # 两个智能体分别选择动作  a_1 = agent.take_action(s[0])  a_2 = agent.take_action(s[1])  # 执行动作，获取下一状态、奖励、终止标志和额外信息  next_s, r, done, info = env.step([a_1, a_2])  # 存储智能体1的经验  transition_dict_1[\'states\'].append(s[0])  transition_dict_1[\'actions\'].append(a_1)  transition_dict_1[\'next_states\'].append(next_s[0])  # 如果获胜，奖励增加100；否则减少0.1(稀疏奖励设计)  transition_dict_1[\'rewards\'].append(r[0] + 100 if info[\'win\'] else r[0] - 0.1)  transition_dict_1[\'dones\'].append(False)  # 存储智能体2的经验(同理)  transition_dict_2[\'states\'].append(s[1])  transition_dict_2[\'actions\'].append(a_2)  transition_dict_2[\'next_states\'].append(next_s[1])  transition_dict_2[\'rewards\'].append(r[1] + 100 if info[\'win\'] else r[1] - 0.1)  transition_dict_2[\'dones\'].append(False)  s = next_s # 更新状态  terminal = all(done) # 当所有智能体都完成时，回合结束 # 记录本回合胜负结果 win_list.append(1 if info[\"win\"] else 0) # 分别使用两个智能体的经验更新策略 agent.update(transition_dict_1) agent.update(transition_dict_2) # 每100个回合更新一次进度条，显示当前胜率 if (i_episode + 1) % 100 == 0:  pbar.set_postfix({ \'episode\': \'%d\' % (num_episodes / 10 * i + i_episode + 1), \'return\': \'%.3f\' % np.mean(win_list[-100:]) # 最近100回合的平均胜率  }) pbar.update(1) # 更新进度条 # 处理胜率数据并绘制曲线 win_array = np.array(win_list) # 每100条轨迹取一次平均，平滑胜率曲线 win_array = np.mean(win_array.reshape(-1, 100), axis=1) episodes_list = np.arange(win_array.shape[0]) * 100 # 计算X轴(回合数) plt.plot(episodes_list, win_array) # 绘制胜率曲线 plt.xlabel(\'Episodes\') # X轴标签 plt.ylabel(\'Win rate\') # Y轴标签 plt.title(\'IPPO on Combat\') # 标题 plt.show() # 显示图像

多智能体强化学习入门：从基础到 IPPO 算法—强化学习(20)

1、什么是多智能体强化学习？