AI：线性代数之向量_多维向量的表示方式

线性代数核心概念深度解析：向量的本质与应用实践 🌟

引言

向量是连接数学抽象与工程实践的桥梁，既是机器学习中的特征载体，也是计算机图形学中的变换工具。本文将从多维度拆解向量核心概念，结合前沿应用场景，构建完整的知识体系框架。

一、向量简介

向量就像一个有方向和大小的箭头。在生活里，从你家到学校，不仅有距离（大小），还有方向，这就能用向量表示。

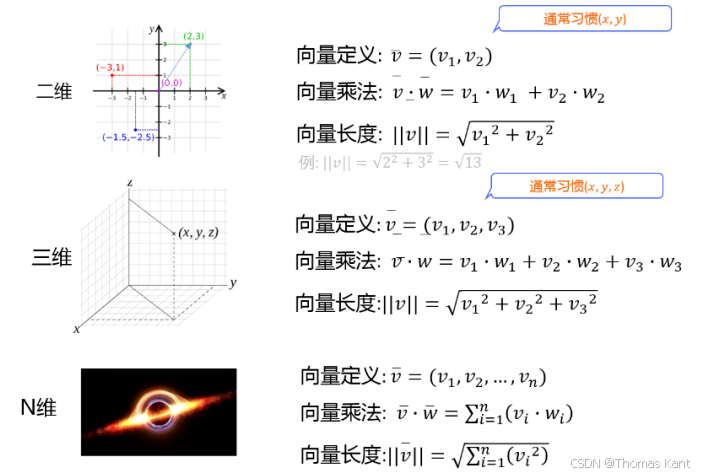
在数学中，向量可以写成一列数字，比如二维向量 v⃗=(23)\\vec{v} = \\begin{pmatrix} 2 \\\\ 3 \\end{pmatrix}v =(23​)，这两个数字分别代表在 $x$ 轴和 $y$ 轴方向上的“长度”。

向量有两种基本运算：

• 加法：对应位置的数字相加。比如 a⃗=(12)\\vec{a} = \\begin{pmatrix} 1 \\\\ 2 \\end{pmatrix}a =(12​)，b⃗=(34)\\vec{b} = \\begin{pmatrix} 3 \\\\ 4 \\end{pmatrix}b =(34​)，那么 a⃗+b⃗=(1+32+4)=(46)\\vec{a} + \\vec{b} = \\begin{pmatrix} 1 + 3 \\\\ 2 + 4 \\end{pmatrix} = \\begin{pmatrix} 4 \\\\ 6 \\end{pmatrix}a +b =(1+32+4​)=(46​) ，就好像你先沿着 a⃗\\vec{a}a 的方向走，再沿着 b⃗\\vec{b}b 的方向走，结果就是 a⃗+b⃗\\vec{a} + \\vec{b}a +b 的方向和长度。
• 数乘：向量的每个数字和一个数相乘。比如 3a⃗=(3×13×2)=(36)3\\vec{a} = \\begin{pmatrix} 3×1 \\\\ 3×2 \\end{pmatrix} = \\begin{pmatrix} 3 \\\\ 6 \\end{pmatrix}3a =(3×13×2​)=(36​)，相当于把向量 a⃗\\vec{a}a 的长度变为原来的3倍。

二、向量的多维表达形式 📐➡️🔢

2.1 代数表示法（⚙️）

• 希腊字母标记：α、β、γ等符号简洁表示向量，避免与标量混淆
• 坐标表示：三维向量v⃗=(x,y,z)\\vec{v} = (x,y,z)v =(x,y,z)可推广到n维空间Rn\\mathbb{R}^nRn，如RGB颜色向量$(255,0,0)$
• 矩阵形式：列向量α=[123]\\alpha = \\begin{bmatrix}1\\\\2\\\\3\\end{bmatrix}α= ​123​ ​本质是$n\times 1$矩阵，便于矩阵运算

2.2 几何诠释（🌌）

• 有向线段：箭头方向表示方向，模长∣∣v⃗∣∣=x2+y2+z2||\\vec{v}|| = \\sqrt{x^2+y^2+z^2}∣∣v ∣∣=x2+y2+z2 ​计算空间距离
• 极坐标转换：二维向量v⃗=(rcos⁡θ,rsin⁡θ)\\vec{v} = (r\\cosθ, r\\sinθ)v =(rcosθ,rsinθ)实现极坐标与笛卡尔坐标转换
• 高维扩展：神经科学中100维向量可描述大鼠神经元活动，时空数据可形成超百万维向量

极坐标

极坐标是一种和咱们平常熟悉的直角坐标不一样的确定位置的方法 。想象你站在一个大广场中心，要描述广场上某个物体的位置。直角坐标像是给广场画了横平竖直的格子，通过物体在横向（x轴）和纵向（y轴）的距离来确定位置。但极坐标呢，思路不太一样。它以你站的这个中心位置作为极点 。从极点出发，画一条射线作为极轴 ，通常极轴水平向右。要确定物体位置，需要两个信息：

• 第一个是距离 ，也就是物体离你有多远，这个距离叫极径，用字母 (r) 表示。比如物体离你10米远，(r) 就是10。
• 第二个是角度 ，是从极轴开始，逆时针旋转到连接你和物体的那条线所形成的角度，这个角度叫极角，用希腊字母 ( \\theta ) 表示 。比如逆时针转了60° ，( \\theta ) 就是60° （在数学里，一般用弧度制表示角度，60° 换算成弧度是 ( \\frac{\\pi}{3} ) ）。

这样，通过极径 (r) 和极角 ( \\theta ) 就能确定物体位置，写成坐标形式就是 ((r, \\theta)) 。比如 ((5, \\frac{\\pi}{4})) ，就表示这个物体距离极点5个单位长度，极角是 ( \\frac{\\pi}{4} ) （也就是45° ）。极坐标在很多地方都有用。比如在雷达定位里，雷达以自身为极点，通过测量目标物体的距离（极径）和方向（极角）来确定目标位置。在数学里，有些图形用极坐标描述会更简单，像圆、阿基米德螺线等。

笛卡尔坐标

笛卡尔坐标就像是给我们生活的空间或者平面，制定了一套非常方便的“地址系统”，用来准确地确定位置。

• 平面笛卡尔坐标：想象你在一张白纸上画画，为了能说清楚纸上每个点的位置，我们画两条互相垂直的线，这两条线就构成了平面笛卡尔坐标系。其中，横着的线叫 $x$ 轴，竖着的线叫 $y$ 轴，它们相交的点叫原点，坐标是 $(0,0)$ 。对于纸上任意一个点 $P$ ，我们从点 $P$ 分别向 $x$ 轴和 $y$ 轴作垂线。垂足在 $x$ 轴上对应的数值就是这个点的 $x$ 坐标，垂足在 $y$ 轴上对应的数值就是这个点的 $y$ 坐标 。这两个坐标组合在一起，写成 $(x,y)$ ，就能独一无二地确定这个点在平面上的位置。比如说，点 $A$ 的 $x$ 坐标是 $3$ ，$y$ 坐标是 $4$ ，我们就可以说点 $A$ 的坐标是 $(3,4)$ ，这样就能在这个平面坐标系里精准地找到点 $A$ 啦。

• 空间笛卡尔坐标：如果从平面拓展到空间，就像我们生活的三维世界，那就需要三条互相垂直的线来构建空间笛卡尔坐标系。除了横着的 $x$ 轴和竖着的 $y$ 轴，还多了一条垂直于纸面指向我们的 $z$ 轴。三条轴相交于原点 $(0,0,0)$ 。对于空间中的任意一点 $Q$ ，我们同样从点 $Q$ 分别向 $x$ 轴、$y$ 轴和 zz