Opencv/Matlab相机标定_matlab 相机标定

技术文档

1、相机标定目标

2、数据准备

3、程序标定

3.1 OpenCV标定

3.2 Matlab标定

4、标定结果应用

5、知识点补充

如何建立像素与实际尺寸的转换关系？

三个矩阵的关系是什么样的？

1、相机标定目标

通过采集已知世界坐标的特征点（如标定板角点）的图像，求解：

内参：焦距（fx, fy）、主点坐标（cx, cy）、畸变系数（k1, k2, p1, p2, k3 等）；
外参：每幅图像对应的旋转矩阵 R 和平移向量 t（描述相机坐标系与世界坐标系的位姿关系）；
最终实现：像素坐标 → 相机坐标 → 世界坐标（实际尺寸）的转换。

2、数据准备

标定板：棋盘格标定板 (需明确每个棋盘格对应的实际距离是多少；标定板角点数为多少，例如下图角点数为6×9)

注：角点的行数应该是偶数，列数应该是奇数

拍摄环境：

光照：均匀光照，避免标定板表面有反光，确保角点清晰可辨（无阴影、无过曝）
相机固定需要固定在某一位置
背景：标定板放置在与实际测量场景一致的平面，避免背景干扰

采集数量：10-20张

位姿变化：

标定板需在视场中呈现不同角度和位置：例如水平放置、倾斜 30°、倾斜 60°、靠近图像左 / 右 / 上 / 下边缘、部分出现在视场角落等（确保覆盖整幅图像的各个区域）；
旋转角度：每次拍摄时，标定板绕自身平面法线旋转不同角度（如 0°、30°、60°），增加位姿多样性；
避免重复位姿（如仅平移不旋转，会导致外参求解退化）。

3、程序标定

3.1 OpenCV标定

C++程序如下：

#include #include #include #include #include #include #include using namespace cv;using namespace std;void main(){ ifstream fin(\"calibdata.txt\"); /* 标定所用图像文件的路径 */ ofstream fout(\"caliberation_result.txt\"); /* 保存标定结果的文件 */ //读取每一幅图像，从中提取出角点，然后对角点进行亚像素精确化 cout << \"开始提取角点………………\"; int image_count = 0; /* 图像数量 */ Size image_size; /* 图像的尺寸 */ Size board_size = Size(7, 10); /* 标定板上每行、列的角点数 */ vector image_points_buf; /* 缓存每幅图像上检测到的角点 */ vector<vector> image_points_seq; /* 保存检测到的所有角点 */ string filename; // int count = -1;//用于存储角点个数。 while (getline(fin, filename)) { image_count++; // 用于观察检验输出 cout << \"image_count = \" << image_count << endl; /* 输出检验*/ // cout <count = \" << count; Mat imageInput = imread(filename); if (image_count == 1) //读入第一张图片时获取图像宽高信息 { image_size.width = imageInput.cols; image_size.height = imageInput.rows; cout << \"image_size.width = \" << image_size.width << endl; cout << \"image_size.height = \" << image_size.height << endl; } /* 提取角点 */ if (0 == findChessboardCorners(imageInput, board_size, image_points_buf)) { cout << \"can not find chessboard corners!\\n\"; //找不到角点 exit(1); } else { Mat view_gray; cvtColor(imageInput, view_gray, COLOR_RGB2GRAY); /* 亚像素精确化 */ // cout << \"执行亚像素精细化\" << endl; find4QuadCornerSubpix(view_gray, image_points_buf, Size(11, 11)); //对粗提取的角点进行精确化 image_points_seq.push_back(image_points_buf); //保存亚像素角点 /* 在图像上显示角点位置 */ // cout << \"图像进行显示\" << endl; drawChessboardCorners(view_gray, board_size, image_points_buf, true); //用于在图片中标记角点 imshow(\"Camera Calibration\", view_gray);//显示图片 waitKey(500);//暂停0.5S } } int total = image_points_seq.size(); cout << \"total = \" << total << endl; int CornerNum = board_size.width * board_size.height; //每张图片上总的角点数 for (int ii = 0; ii < total; ii++) { //if (0 == ii % CornerNum)// 24 是每幅图片的角点个数。此判断语句是为了输出 图片号，便于控制台观看 //{ // int i = -1; // i = ii / CornerNum; // int j = i + 1; // cout < 第 \" << j < : \" << endl; //} //if (0 == ii % 3) // 此判断语句，格式化输出，便于控制台查看 //{ // cout << endl; //} //else //{ // cout.width(10); //} //输出所有的角点 cout << \"第\" << ii + 1 << \"张图像角点信息\"; cout <\" << image_points_seq[ii][0].x; cout <\" << image_points_seq[ii][0].y << endl; } cout << \"角点提取完成！\\n\"; //以下是摄像机标定 cout << \"开始标定………………\"; /*棋盘三维信息*/ Size square_size = Size(18, 18); /* 实际测量得到的标定板上每个棋盘格的大小 */ vector<vector> object_points; /* 保存标定板上角点的三维坐标 */ /*内外参数*/ Mat cameraMatrix = Mat(3, 3, CV_32FC1, Scalar::all(0)); /* 摄像机内参数矩阵 */ vector point_counts; // 每幅图像中角点的数量 Mat distCoeffs = Mat(1, 5, CV_32FC1, Scalar::all(0)); /* 摄像机的5个畸变系数：k1,k2,p1,p2,k3 */ vector rvecsMat; /* 每幅图像的旋转向量 */ vector tvecsMat; /* 每幅图像的平移向量 */ /* 初始化标定板上角点的三维坐标 */ int i, j, t; for (t = 0; t < image_count; t++) { vector tempPointSet; for (i = 0; i < board_size.height; i++) { for (j = 0; j < board_size.width; j++) { Point3f realPoint; /* 假设标定板放在世界坐标系中z=0的平面上 */ realPoint.x = i * square_size.width; realPoint.y = j * square_size.height; realPoint.z = 0; tempPointSet.push_back(realPoint); } } object_points.push_back(tempPointSet); } /* 初始化每幅图像中的角点数量，假定每幅图像中都可以看到完整的标定板 */ for (i = 0; i < image_count; i++) { point_counts.push_back(board_size.width * board_size.height); } /* 开始标定 */ calibrateCamera(object_points, image_points_seq, image_size, cameraMatrix, distCoeffs, rvecsMat, tvecsMat, 0); cout << \"标定完成！\\n\"; //对标定结果进行评价 cout << \"开始评价标定结果………………\\n\"; double total_err = 0.0; /* 所有图像的平均误差的总和 */ double err = 0.0; /* 每幅图像的平均误差 */ vector image_points2; /* 保存重新计算得到的投影点 */ cout << \"\\t每幅图像的标定误差：\\n\"; fout << \"每幅图像的标定误差：\\n\"; for (i = 0; i < image_count; i++) { vector tempPointSet = object_points[i]; /* 通过得到的摄像机内外参数，对空间的三维点进行重新投影计算，得到新的投影点 */ projectPoints(tempPointSet, rvecsMat[i], tvecsMat[i], cameraMatrix, distCoeffs, image_points2); /* 计算新的投影点和旧的投影点之间的误差*/ vector tempImagePoint = image_points_seq[i]; Mat tempImagePointMat = Mat(1, tempImagePoint.size(), CV_32FC2); Mat image_points2Mat = Mat(1, image_points2.size(), CV_32FC2); for (int j = 0; j < tempImagePoint.size(); j++) { image_points2Mat.at(0, j) = Vec2f(image_points2[j].x, image_points2[j].y); tempImagePointMat.at(0, j) = Vec2f(tempImagePoint[j].x, tempImagePoint[j].y); } err = norm(image_points2Mat, tempImagePointMat, NORM_L2); total_err += err /= point_counts[i]; std::cout << \"第\" << i + 1 << \"幅图像的平均误差：\" << err << \"像素\" << endl; fout << \"第\" << i + 1 << \"幅图像的平均误差：\" << err << \"像素\" << endl; } std::cout << \"总体平均误差：\" << total_err / image_count << \"像素\" << endl; fout << \"总体平均误差：\" << total_err / image_count << \"像素\" << endl << endl; std::cout << \"评价完成！\" << endl; //保存定标结果 std::cout << \"开始保存定标结果………………\" << endl; Mat rotation_matrix = Mat(3, 3, CV_32FC1, Scalar::all(0)); /* 保存每幅图像的旋转矩阵 */ fout << \"相机内参数矩阵：\" << endl; fout << cameraMatrix << endl << endl; fout << \"畸变系数：\\n\"; fout << distCoeffs << endl << endl << endl; for (int i = 0; i < image_count; i++) { fout << \"第\" << i + 1 << \"幅图像的旋转向量：\" << endl; fout << rvecsMat[i] << endl; /* 将旋转向量转换为相对应的旋转矩阵 */ Rodrigues(rvecsMat[i], rotation_matrix); fout << \"第\" << i + 1 << \"幅图像的旋转矩阵：\" << endl; fout << rotation_matrix << endl; fout << \"第\" << i + 1 << \"幅图像的平移向量：\" << endl; fout << tvecsMat[i] << endl << endl; } std::cout << \"完成保存\" << endl; fout << endl; system(\"pause\"); return;}

针对不同类型棋盘格程序修改如下：

例如针对角点数量为6×9的棋盘格标定板，其中每个棋盘格对应实际距离为18mm

则修改：

Size board_size = Size(6, 9); /* 标定板上每行、列的角点数 */

Size square_size = Size(18, 18); /* 实际测量得到的标定板上每个棋盘格的大小 */

程序准备文件：calibdata.txt，内容为所有标定图像的路径

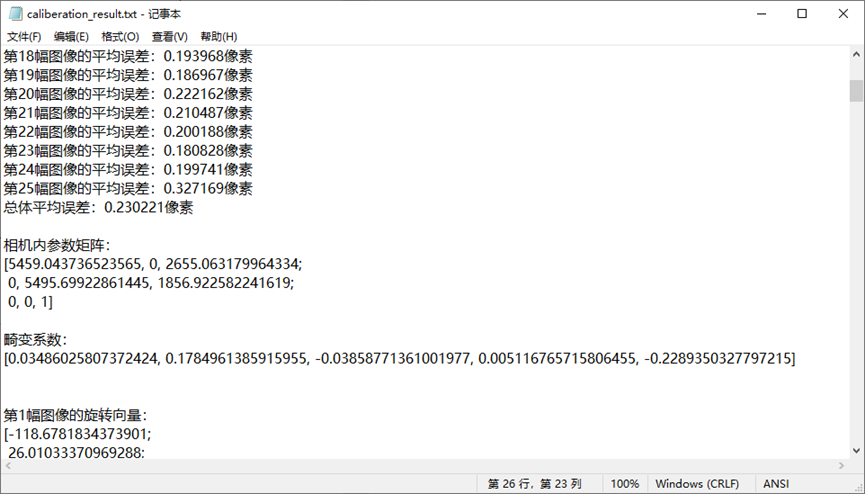
程序结果输出文件：caliberation_result.txt，包含每幅图像对应误差、内参矩阵、畸变系数等等

3.2 Matlab标定

Matlab R2022a

打开matlab：

进入APP，找到相机标定：

添加标定图像：

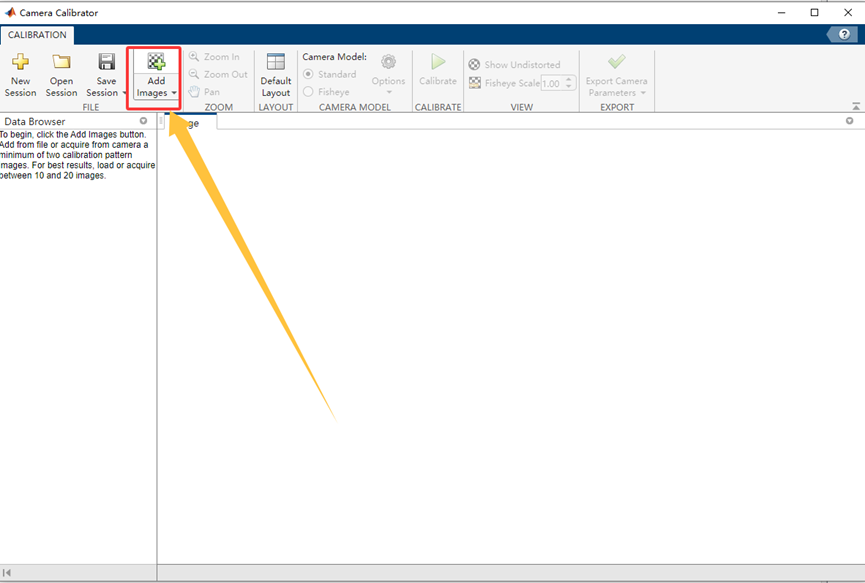
选择好对应的标定板类型以及对应的尺寸：

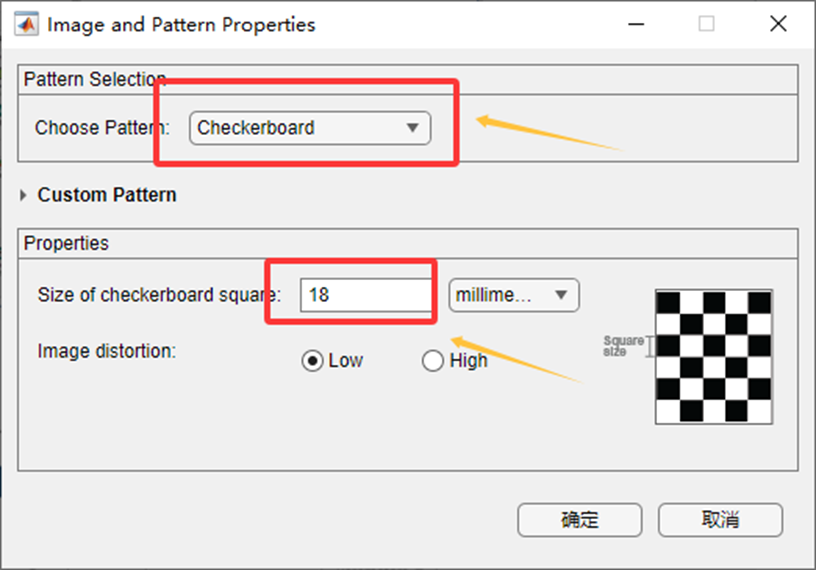
确定之后即可进行角点检测，等待结果输出如下：（若拍摄质量不好，会弹出提示框，至少要保证可以正常检测的图像为10张）

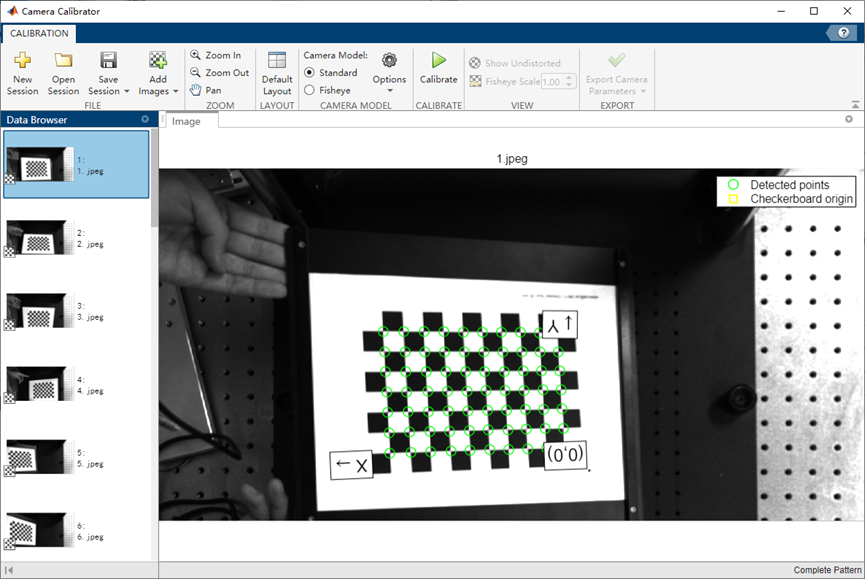
待上述结果输出之后，检查角点检测准确性，之后点击标定：

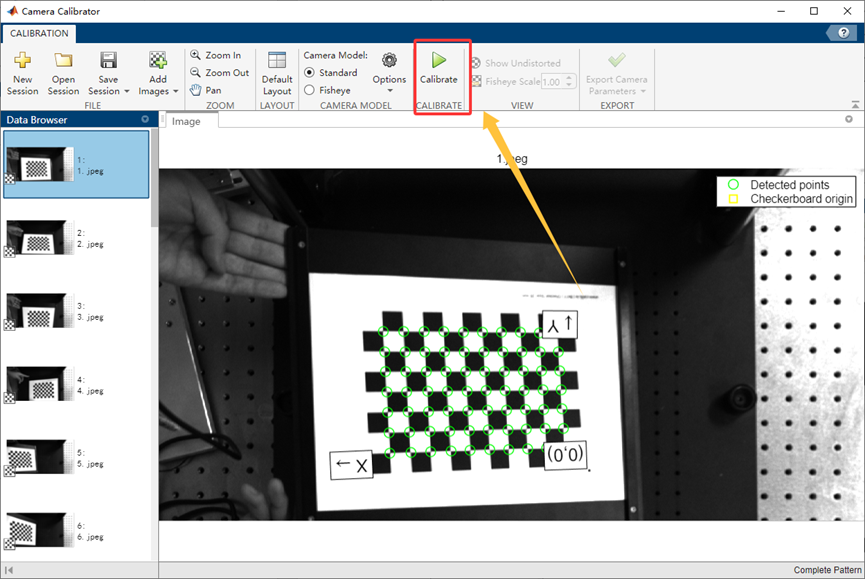
标定完成之后，即可输出结果：其中误差评估可选可不选

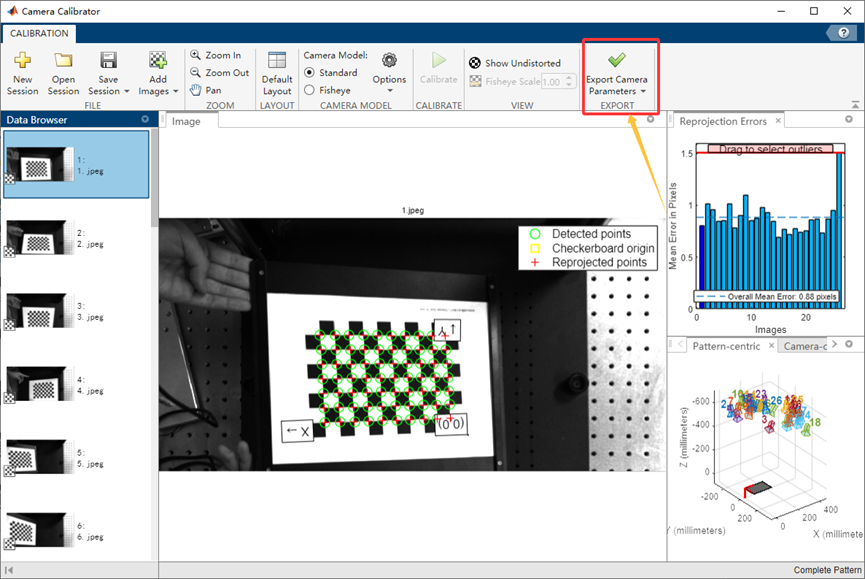
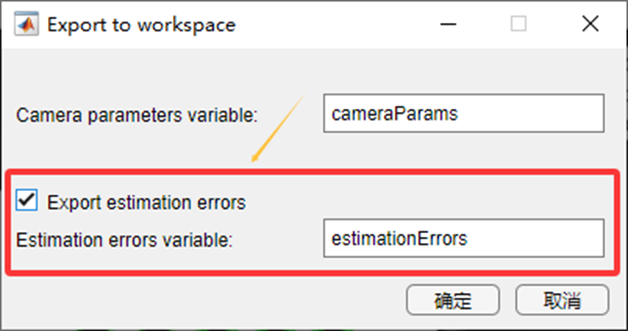
输出结果如下：可通过双击查看具体信息

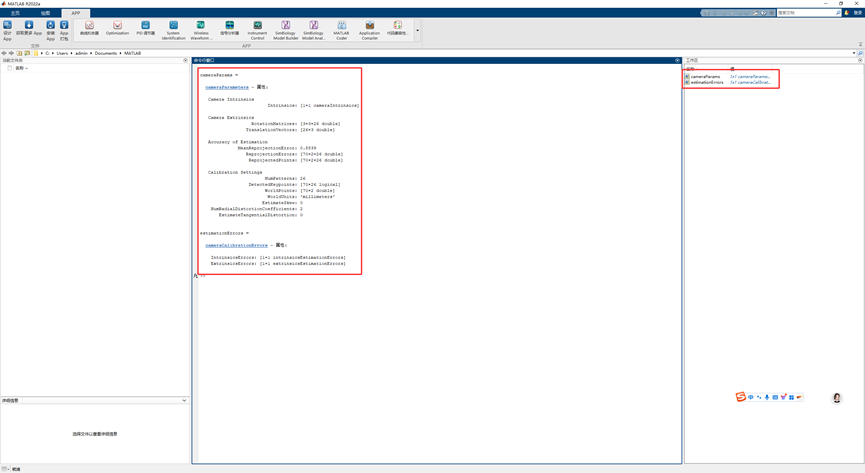
4、标定结果应用

#include #include #include using namespace cv;using namespace std;int main() { // 步骤1: 定义相机内参 Mat cameraMatrix = (Mat_(3, 3) << 5470.847189303858, 0, 2641.664843053581, // fx, 0, cx 0, 5509.530534684527, 1850.794633728518, // 0, fy, cy 0, 0, 1 // 0, 0, 1 ); // 畸变系数: k1, k2, p1, p2, k3 Mat distCoeffs = (Mat_(1, 5) << 0.04131358839568192, 0.1474656470505348, -0.03889415749765213, 0.004097644223187673, -0.1519331362471956); // 步骤2: 定义外参（相机相对于世界坐标系的位姿） // 旋转向量（Rodrigues形式），需转换为旋转矩阵 Mat rvec = (Mat_(3, 1) << -0.03022492372659337, -3.093018942247979, 0.09715930931014681); Mat R; Rodrigues(rvec, R); // 转换为3x3旋转矩阵 // 平移向量 Mat tvec = (Mat_(3, 1) << 36.16611771945472, -93.12036353800454, 715.6710066064154); // 单位：mm // 步骤3: 加载图像 Mat distortedImage = imread(\"C:/Users/admin/Desktop/temp/Camera_calibration_image/Pic_2025_07_10_153747_2.jpeg\"); if (distortedImage.empty()) { cout << \"无法加载图像！\" << endl; return -1; } // 步骤4: 畸变校正 Mat undistortedImage; undistort(distortedImage, undistortedImage, cameraMatrix, distCoeffs); // 步骤5: 计算单应矩阵H（假设物体在Z=0平面） Mat H; // 方法1、通过相机标定内参和外参计算H // H = K * [R|t]，其中[R|t]取前两列+平移向量 // 从旋转矩阵R中提取前两列（R1和R2） 这里不使用第三列，第三列对应z轴的旋转 Mat R1 = R.col(0); // 旋转矩阵的第1列 Mat R2 = R.col(1); // 旋转矩阵的第2列 // 构建3x3矩阵 [R1 R2 t]（将R的前两列与平移向量t组合） Mat R1_R2_t = Mat::zeros(3, 3, CV_64F); R1.copyTo(R1_R2_t.col(0)); R2.copyTo(R1_R2_t.col(1)); tvec.copyTo(R1_R2_t.col(2)); // 计算单应矩阵 H = K * [R1 R2 t] H = cameraMatrix * R1_R2_t; // 单应矩阵归一化（可选，但通常有助于提高稳定性） H = H / H.at(2, 2); // 方法2、使用我们已知点坐标计算H，准确性较低 // 假设我们已知图像中某点的像素坐标，计算其实际物理坐标 //vector imagePoints; //vector worldPoints; //// 添加对应点（示例：4个角点） //imagePoints.push_back(Point2f(1541, 1013)); // 像素坐标 //imagePoints.push_back(Point2f(2089, 1005)); //imagePoints.push_back(Point2f(1557, 1713)); //imagePoints.push_back(Point2f(2245, 1701)); //// 由于此方法为拟合方法，若实际数值与坐标数值差别很大，最终计算结果误差会很大，故下面设置scaleFactor //double scaleFactor = 24.0; //worldPoints.push_back(Point2f(0, 0)); // 实际坐标（单位：mm） //worldPoints.push_back(Point2f(90 * scaleFactor, 0)); //worldPoints.push_back(Point2f(0, 90 * scaleFactor)); //worldPoints.push_back(Point2f(90 * scaleFactor, 90 * scaleFactor)); //// 计算单应矩阵（更准确的方法，替代上面的简化计算） //H = findHomography(imagePoints, worldPoints, RANSAC); Mat H_inv = H.inv(); // 逆矩阵：用于从像素到世界坐标的转换 // 步骤6: 选择图像中的物体并计算尺寸 vector objectCorners; // 原始图像中角点 objectCorners.push_back(Point2f(3251, 1313)); // 物体在图像中的角点 objectCorners.push_back(Point2f(3377, 1363)); objectCorners.push_back(Point2f(4673, 1859)); // 将原图对应的像素点转换到校正后图像像素点 vector undistortedCorners; undistortPoints(objectCorners, undistortedCorners, cameraMatrix, distCoeffs); // 将归一化坐标转换到像素坐标 for (auto& pt : undistortedCorners) { pt.x = pt.x * cameraMatrix.at(0, 0) + cameraMatrix.at(0, 2); pt.y = pt.y * cameraMatrix.at(1, 1) + cameraMatrix.at(1, 2); } // 计算像素点之间的距离 double obj1_dis = norm(objectCorners[1] - objectCorners[0]); double obj2_dis = norm(objectCorners[2] - objectCorners[0]); double undistorted1_dis = norm(undistortedCorners[1] - undistortedCorners[0]); double undistorted2_dis = norm(undistortedCorners[2] - undistortedCorners[0]); // 转换为世界坐标 vector worldObjectCorners; perspectiveTransform(undistortedCorners, worldObjectCorners, H_inv); // 步骤7: 计算物体尺寸 // 计算长度 double length = norm(worldObjectCorners[2] - worldObjectCorners[0]); cout << \"物体长度: \" << length << \" 毫米\" << endl; cout << \"校正前对应坐标：(\" << objectCorners[0].x << \" , \" << objectCorners[0].y << \")---(\"; cout << objectCorners[1].x << \" , \" << objectCorners[1].y << \")---(\" << objectCorners[2].x << \" , \" << objectCorners[2].y << \")\" << endl; cout << \"校正后对应坐标：(\" << undistortedCorners[0].x << \" , \" << undistortedCorners[0].y << \")---(\"; cout << undistortedCorners[1].x << \" , \" << undistortedCorners[1].y << \")---(\" << undistortedCorners[2].x << \" , \" << undistortedCorners[2].y << \")\" << endl; cout << \"校正前前两个点像素距离：\" << obj1_dis << \" ; 后两个点像素距离：\" << obj2_dis << endl; cout << \"校正后前两个点像素距离：\" << undistorted1_dis << \" ; 后两个点像素距离：\" << undistorted2_dis << endl; // 步骤9: 保存结果 imwrite(\"原始图像.jpg\", distortedImage); imwrite(\"校正后图像.jpg\", undistortedImage); system(\"pause\"); return 0;}

矫正前图像：