刷题记录——动态规划
1.《过马卒》一道入门dp
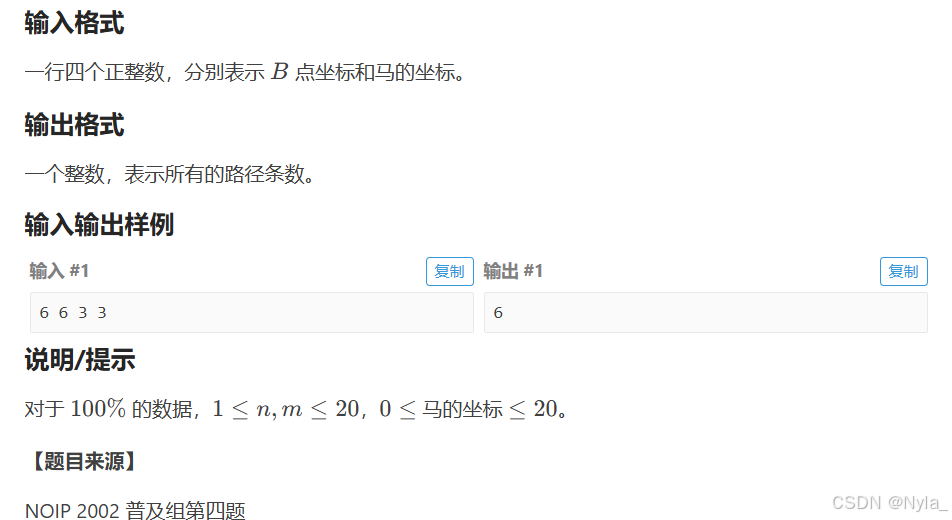
借着本题还玩了一晚上象棋(bushi
本蒟蒻终于(复述)了一遍佬的答案,思路是这样的
理解题目
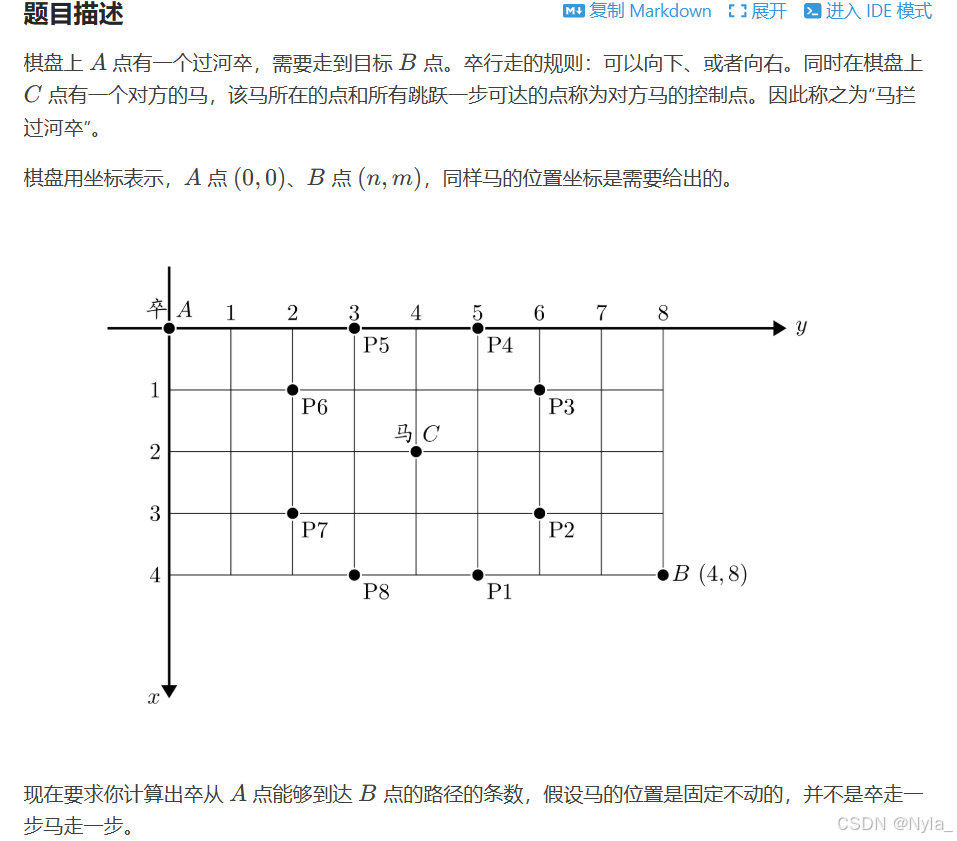
在过河卒问题里,棋盘上有一个卒和一匹马。卒只能向下或者向右移动,马会控制它所在位置以及按照 “日” 字规则能跳到的位置,卒不能经过马控制的点。
我们的目标是计算卒从棋盘左上角走到右下角有多少种不同的路径。
检查点是否被马控制的函数 check
根据马走 “日” 字的规则,马控制的点满足两个条件:
一是两点横纵坐标差值的绝对值之和为 3,二是横纵坐标差值绝对值的最大值为 2。同时满足这两个条件的点就是马控制的点,返回 true,否则返回 false。
动态规划计算路径数量
动态规划状态转移方程
在过河卒问题里,设 f[i][j] 表示卒走到坐标 (i, j) 位置的路径数量,也就是说,卒只能从上方 (i - 1, j) 或者左方 (i, j - 1) 走到当前位置 (i, j),那么到达 (i, j) 的路径数量就是到达上方点和左方点的路径数量之和。状态转移方程为
f[i][j] = f[i - 1][j] + f[i][j - 1](前提是该点没有被马控制)。
坐标加 2 避免边界问题
终点坐标和马的坐标,然后都加 2 是为了避免边界处理的麻烦,相当于给棋盘的最上面和最左边空出两行两列。
假设我们不把坐标加上 2,直接从 (0, 0) 开始计算。当卒在棋盘的最左边一列(即 j = 0)时,在计算 f[i][0] 时,根据状态转移方程需要用到 f[i][0 - 1],也就是 f[i][-1],这就出现了数组越界的情况,因为数组下标不能为负数。
如果坐标只加 1,在处理棋盘最左上角的实际起点位置(加 1 后变为 (1, 1) )时,还是会面临边界问题。例如,当计算 f[1][1] 时,根据状态转移方程需要用到 f[1 - 1][1] (即 f[0][1] )和 f[1][1 - 1] (即 f[1][0] ),这样就出现了数组越界的情况,因为数组下标为 0 可能不在我们有效的棋盘范围内。
空间优化:二维数组转化为一维数组——滚动数组
这个地方我觉得语言描述很难看懂,也可能是本人语言能力和理解力不行,其实写一遍两层for循环就知道咋回事了,外循环是行,内循环是列,二维数组转化为一维数组:f [ j ]表示到 j 列的路径数,每增加一行,更新一遍f [ j ],即
f [ j ] = f [ j ] + f [ j - 1 ]
滚动数组其实就是复用
这里举例子说明。
例如从(0,0)走到(2,2)(坐标加2后,即从(2,2)走到(4,4) )
初始f [ 2 ]=1
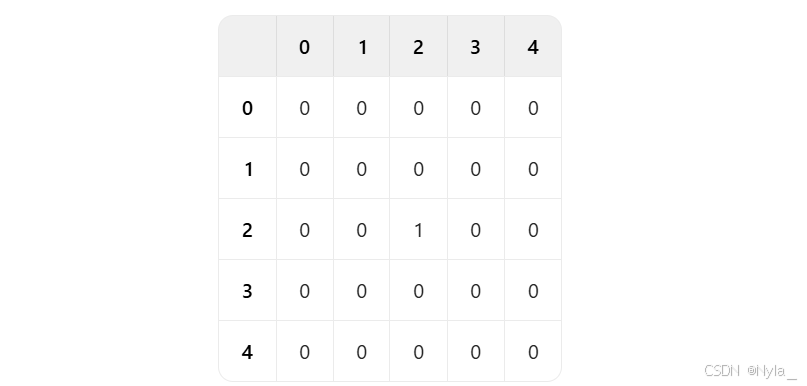
计算第 2 行(i = 2),f [ 2 ]=1, f [ 3 ]=1, f [ 4 ]=1
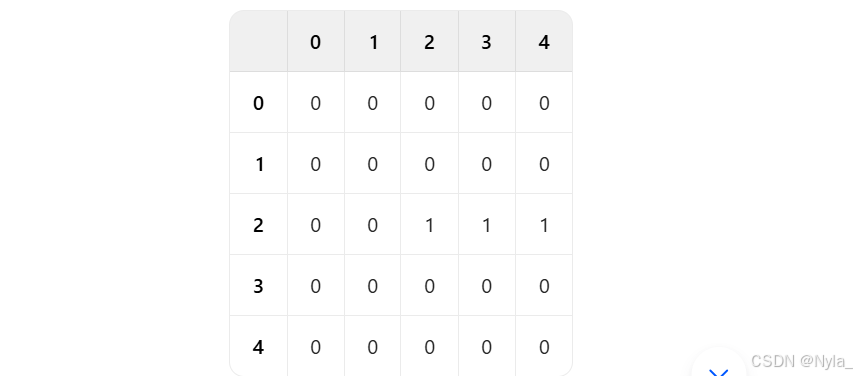
计算第 3 行(i = 3),f [ 2 ]=1, f [ 3 ]=2, f [ 4 ]=3
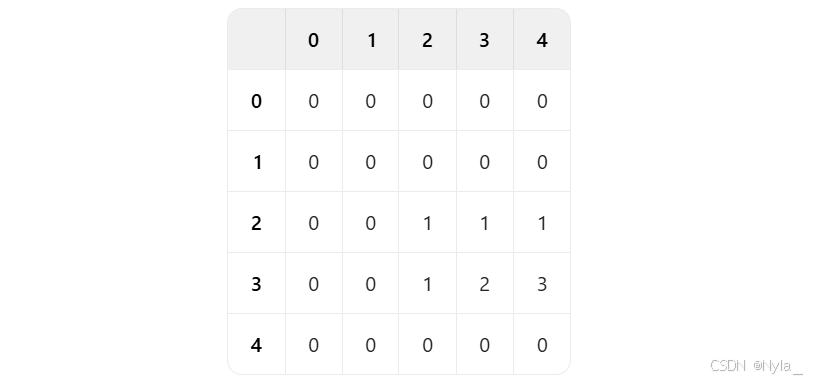
计算第 4 行(i = 4) f [ 2 ]=1, f [ 3 ]=3, f [ 4 ]=6
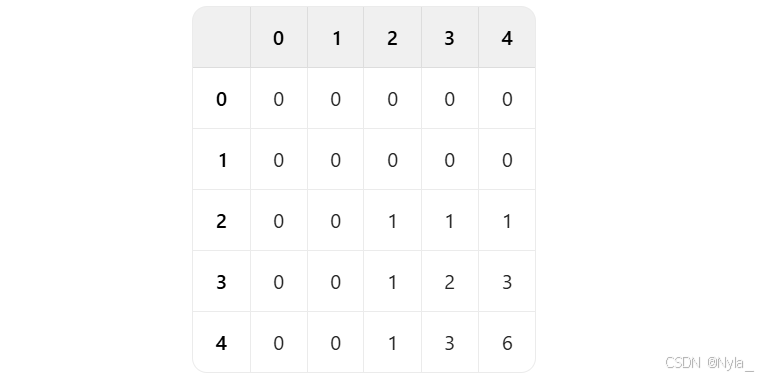
#include using namespace std;#define ll long longint dx, dy, mx, my;ll f[25];bool check(int x, int y){ if (x==mx && y==my) return 1; return (abs(x-mx)+abs(y-my)==3 && max(abs(x-mx), abs(y-my))==2);}int main(){ cin >> dx >>dy >>mx >>my; dx += 2; dy += 2; mx += 2; my += 2; f[2]=1; for (int i=2; i<=dx; i++){ for (int j=2; j<=dy; j++){ if (check(i, j)) { f[j]=0; continue; //直接跳到for循环的下一次迭代 } f[j] += f[j-1]; } } cout << f[dy] <<endl; return 0;} 2.最长上升子序列(一道dp板子题)
B3637
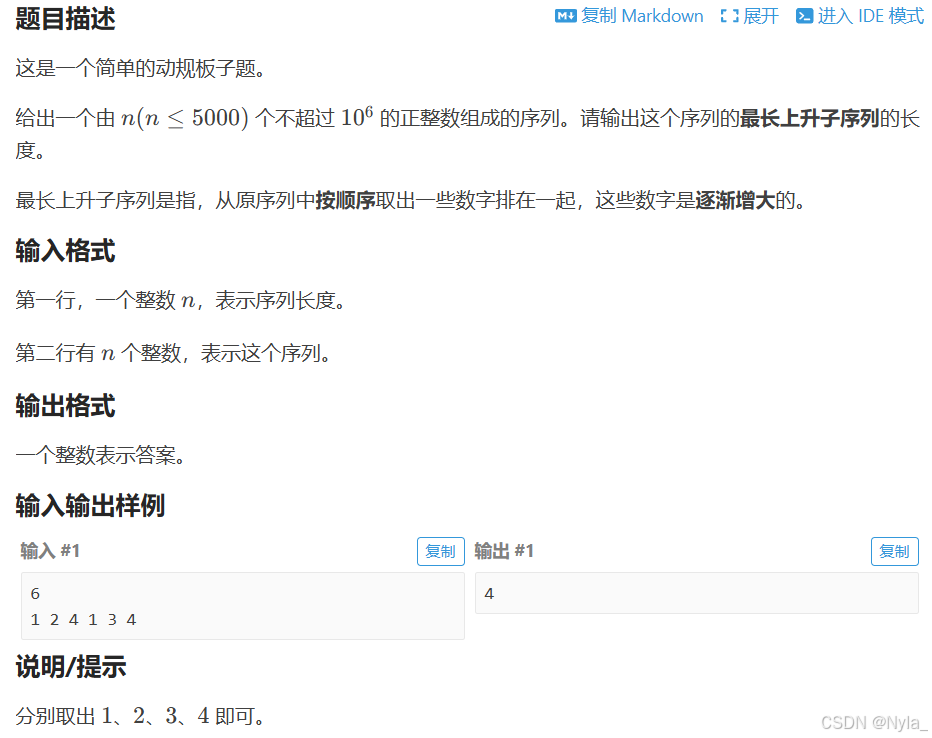

思路很简单,两层for循环,但本蒟蒻还是看的题解才写出来...
#include using namespace std;int main(){ int a[5010], n; cin >> n; for (int i=1; i> a[i]; } vector f(n+1, 1); for (int i=1; i<=n; i++){ for (int j=1; j<=i; j++){ if (a[j]<a[i]) { f[i] = max(f[i], f[j]+1); } } } int result = f[1]; for (int i=1; iresult) result = f[i]; } cout << result <<endl; return 0;}3.最大子段和
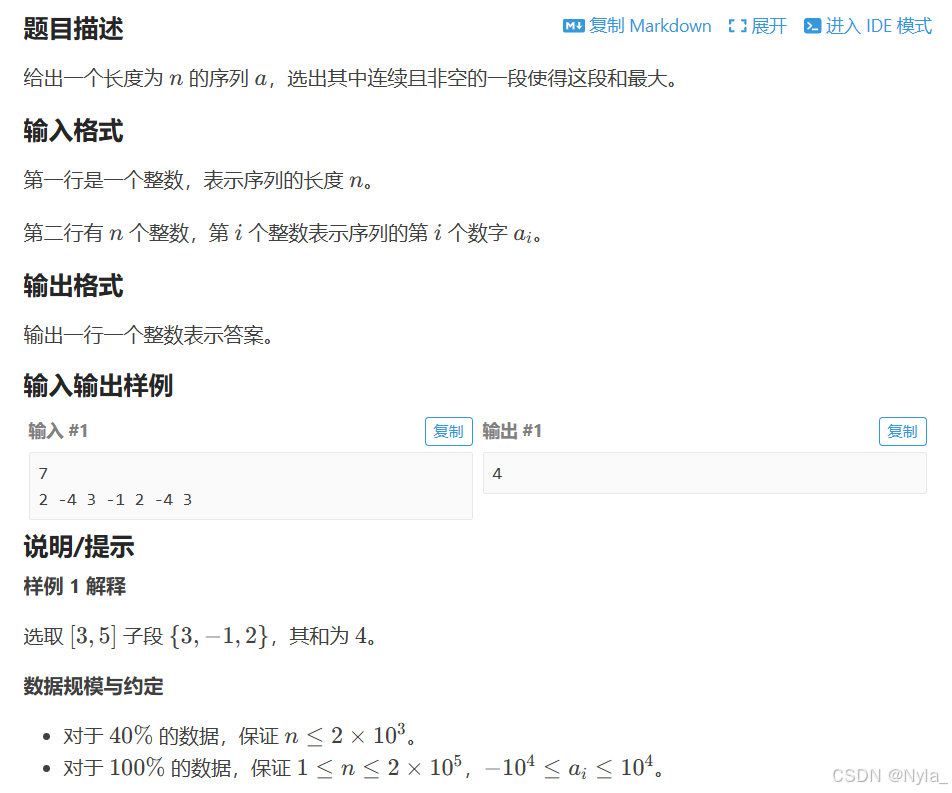
本题仍然参考大佬的题解
引入b [ i ] ,表示循环到 i 时,第 i 个数所在的有效序列的和
- 第一个数为一个有效序列
- 如果一个数加上上一个有效序列得到的结果比这个数大,那么该数也属于这个有效序列。
- 如果一个数加上上一个有效序列得到的结果比这个数小,那么这个数单独成为一个新的有效序列
#include using namespace std;int n, a[200010], b[200010];//b[i]表示循环到i时,第i个数所在的有效序列的和int main(){ cin >> n; for (int i=1; i> a[i]; } for (int i=1; ia[i]) b[i]=b[i-1]+a[i]; else b[i]=a[i]; } int result =b[1]; for (int i=1; iresult) result = b[i]; } cout << result<< endl; return 0;}大佬还对空间复杂度进行了优化,直接O(1)了,鼠鼠拜服,学习一下这种写法。
就是把a数组和b数组都优化成1个变量,并且是在求数组b[ ] 的过程中找最值。
#include using namespace std;int n, a, b, ans=-10010;int main(){ cin >> n; for (int i=1; i> a; if (i==1) b=a; else b = max(a, a+b); ans = max(ans, b); } cout << ans<< endl; return 0;}4.丝绸之路
P3399

写到本题的时候本蒟蒻还没悟怎么用动态规划思想解题,然后又又又看题解里大佬说推状态转移方程,动态规划思想的核心难道是推推状态转移方程(?,2025年AI已经发展到如此规划,本蒟蒻仍然学习不好好利用有效工具,罪过,下面是豆包老师的总结:
动态规划(Dynamic Programming,简称 DP)是一种通过把原问题分解为相对简单的子问题,并保存子问题的解来避免重复计算,从而解决复杂问题的算法策略。下面详细解释动态规划的思想、状态转移方程以及如何刷题做到举一反三。
动态规划思想核心
动态规划主要基于两个核心特性:最优子结构和重叠子问题。!!!
最优子结构
一个问题的最优解可以由其子问题的最优解组合而成。也就是说,大问题的最优解包含了小问题的最优解。例如在过河卒问题中,到达某个点的最优路径数量(这里路径数量的最优就是最多路径)可以由到达其上方点和左方点的路径数量推导出来,即 f[i][j] = f[i - 1][j] + f[i][j - 1] ,这体现了最优子结构的特性。
重叠子问题
在求解问题的过程中,很多子问题会被重复计算。动态规划通过保存这些子问题的解(通常使用数组),避免了重复计算,从而提高了算法的效率。比如在斐波那契数列问题中,计算 F(n) 时会多次用到 F(n - 1) 和 F(n - 2) ,使用动态规划可以把已经计算过的 F(k) 的值保存起来,下次再需要时直接使用,而不是重新计算。
状态转移方程
状态转移方程是动态规划的关键,它描述了如何从子问题的解推导出原问题的解。推导状态转移方程一般可以按以下步骤进行:
定义状态
明确问题的状态表示,也就是用什么来描述子问题。例如在背包问题中,状态可以定义为 dp[i][j] ,表示前 i 个物品放入容量为 j 的背包中所能获得的最大价值。
分析状态转移
考虑状态之间的转移关系,即如何从已知的状态推导出未知的状态。这需要分析问题的规则和约束条件。比如在过河卒问题中,由于卒只能向右或向下走,所以到达 (i, j) 点的路径数量等于到达 (i - 1, j) 点和 (i, j - 1) 点的路径数量之和,得到状态转移方程 f[i][j] = f[i - 1][j] + f[i][j - 1] 。
边界条件
确定状态转移的边界情况,也就是最简单的子问题的解。例如在过河卒问题中,起点的路径数量为 1,即 f[2][2] = 1 ;在斐波那契数列问题中,F(0) = 0 ,F(1) = 1 。
111111111111111111111
下面回到本题
显然,状态转移方程:
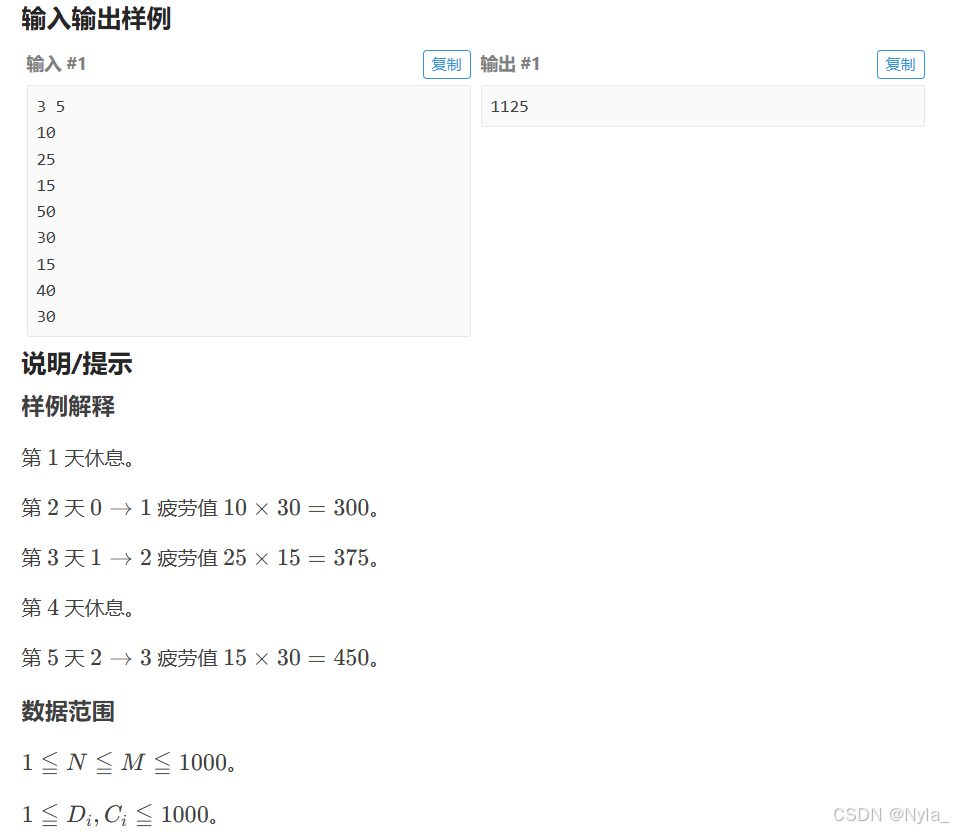
f[i][j] = min(f[i][j - 1], f[i - 1][j - 1] + D[i] * C[j])
f[i][j - 1]的含义:它表示在第j - 1天已经到达了第i号城市,而在第j天选择休息,不进行移动。由于休息不会产生额外的疲劳度,所以在第j天到达第i号城市的最少疲劳度就等于第j - 1天到达该城市的最少疲劳度。f[i - 1][j - 1] + D[i] * C[j]的含义:f[i - 1][j - 1]表示在第j - 1天到达了第i - 1号城市的最少疲劳度。D[i]是第i - 1号城市到第i号城市的距离,C[j]是第j天的气候恶劣值,那么D[i] * C[j]就是在第j天从第i - 1号城市移动到第i号城市所产生的疲劳度。所以f[i - 1][j - 1] + D[i] * C[j]表示在第j天从第i - 1号城市移动到第i号城市的总疲劳度。
#include using namespace std;int n, m, d[1010], c[1010], f[1010][1010];const int INF=2139063143;int main(){ memset(f,0x7f,sizeof(f)); cin >> n>> m; for (int i=1; i> d[i]; } for (int i=1; i> c[i]; } for (int i=0;i<=m;i++) f[0][i]=0; //第i天在第0城市 for (int i=1; i<=n; i++){ for (int j=i; j<=m-(n-i); j++){ //到第i个城市最少用了i天,最多m-(n-i)天 f[i][j] = min (f[i][j-1], f[i-1][j-1]+d[i]*c[j]); } } int ans=f[n][n]; for (int i=n; i<=m; i++){ if (f[n][i]<ans) ans = f[n][i]; } cout << ans <<endl; return 0;}5.最长前缀
P1470

 读题就读半天,有点kmp的感觉,按前面dp的思想没找到子结构,哎,上题解
读题就读半天,有点kmp的感觉,按前面dp的思想没找到子结构,哎,上题解
豆包老师的题目理解比较直观:
- 题目理解:
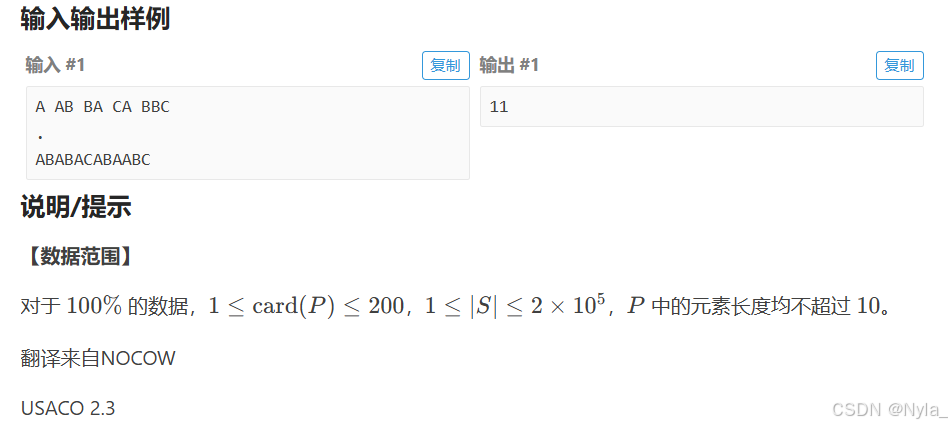
- 想象你有一堆积木(集合中的字符串),然后有一条很长的积木轨道(字符串)。你要从轨道的开头开始,看看最多能用多少积木铺满轨道开头的部分,这里的积木就是集合中的字符串,铺满就是轨道开头部分能拆分成集合中的字符串。
- 例如,集合有 “AB”“BC”,字符串是 “ABBC”,那么最长前缀就是 “ABBC”,因为它可以拆分成 “AB” 和 “BC”,这两个都在集合中。
下面是引入f数组存储结果
- 动态规划状态定义:
- 我们定义表示字符串的前个字符(也就是)是否能拆分成集合中的元素。
- 比如,如果为真,那就说明字符串的前个字符可以由集合中的元素组成。
判断方法的核心(子问题和重叠子问题):
状态转移的逻辑
状态转移的本质是利用已经解决的子问题的解来求解更大的子问题。具体到本题中,对于 f(i)(判断前 i 个字符能否拆分),我们需要考虑前面已经计算出的 f(j)(j < i)的值。
- 前提条件:如果
f(j)为true,说明字符串S的前j个字符已经可以拆分成集合P中的元素。 - 检查新子串:接下来,我们需要检查从第
j + 1个字符到第i个字符组成的子串(即S[j:i])是否在集合P中。如果这个子串在集合P中,那么就意味着我们可以在前j个字符拆分的基础上,再加上这个新的子串,从而使得前i个字符也能拆分成集合P中的元素,此时f(i)就可以设为true。
if(f[j]=true && s[j+1...i]为集合P中的一个字符串(j从i~1 到 1~10 枚举) f[i]=trueelse f[i]=false; 思路说完了。
下面记录一下中间用到的几个函数:
set p;set容器:元素唯一性+字典序
std::set 是一种用于存储唯一元素的容器,它会自动对元素进行排序,默认按照元素的升序排列。集合中的每个元素都是唯一的,不存在重复元素。在本题里,我们用 set 来存储集合 P 中的字符串元素,保证每个字符串只出现一次。
p.insert(pi);insert():向集合p中插入元素pi
if (f[j] && p.count(sl)>0)count 方法查找元素是否存在。count 方法返回集合中某个元素的数量,由于 std::set 中元素唯一,所以返回值要么是 0(元素不存在),要么是 1(元素存在)。
string sl=s.substr(j, i-j);S.substr(j, i - j)是std::string类的一个成员函数,用于截取字符串S中从索引j开始,长度为i - j的子串,并将其存储到sub变量中。- 例如,如果
S = \"ABCDE\",j = 1,i = 3,那么sub就是\"BC\"。
#include using namespace std;set p;const int maxc=200010;bool f[maxc];int main(){ string pi; while (cin >> pi && pi!=\".\"){ p.insert(pi); } string s; string si; while (cin >> si){ s += si; } f[0] = true; int n = s.size(); for (int i=1; i=0 && i-j0){ f[i] = true; break; } } } int result = 0; for (int i=n; i>=0; i--){ if (f[i]){ result = i; break; } } cout << result <<endl; return 0;}6.序列取数
P1430
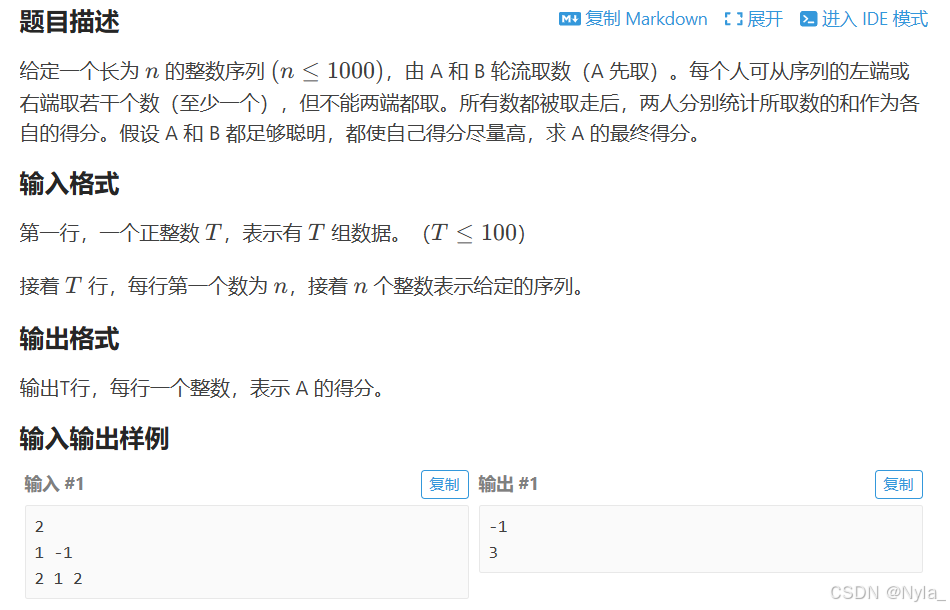
每次取完剩下的都是原序列的连续子序列,所以子问题就是:剩余序列里先手能得的最大分。
A和B都足够聪明:每次A取完后,B是剩余序列的先手。
这题的解对我来说真的是很麻烦了,但其实也都是一个一个模块组成,去除常规的辅助的模块,核心的解题模块其实也就那几行。
然而此题AC的还是很不容易,本蒟蒻还有点一知半解。
// 从左端取数的情况l[i][j] = a[i] + max(l[i + 1][j], sum[j] - sum[i] - max(l[i + 1][j], r[i + 1][j]));// 从右端取数的情况r[i][j] = a[j] + max(r[i][j - 1], sum[j - 1] - sum[i - 1] - max(l[i][j - 1], r[i][j - 1]));这两行代码是动态规划求解该博弈问题的核心状态转移方程,下面详细解释其含义和逻辑。
整体思路
在这个博弈问题中,有一个整数序列 a,两个玩家轮流从序列的左端或右端取数,目标是让先手玩家获得最大得分。我们定义了两个二维数组 l[i][j] 和 r[i][j] 来辅助求解,其中:
l[i][j]表示当先手玩家从区间[i, j]的左端开始取数时,先手玩家能获得的最大得分。r[i][j]表示当先手玩家从区间[i, j]的右端开始取数时,先手玩家能获得的最大得分。
l[i][j] = a[i] + max(l[i + 1][j], sum[j] - sum[i] - max(l[i + 1][j], r[i + 1][j]));详细解释

#include using namespace std;const int N = 1002;long long a[N], sum[N];long long l[N][N], r[N][N]; //从左端和右端取数的最大值long long score(int n, long long a[]) { // 计算前缀和 sum[0] = 0; for (int i = 1; i <= n; i++) { sum[i] = sum[i - 1] + a[i]; } // 初始化,当 i == j 时,l[i][i] 和 r[i][i] 都为 a[i] for (int i = 1; i <= n; i++) { l[i][i] = r[i][i] = a[i]; } // 枚举子序列长度 for (int len = 1; len < n; len++) { for (int i = 1; i + len > t; while (t--) { int n; cin >> n; for (int i = 1; i > a[i]; } cout << score(n, a) << endl; } return 0;}

