网站导航
> 技术文档 > 多目标优化|HKELM混合核极限学习机+NSGAII算法工艺参数优化、工程设计优化，四目标（最大化输出y1、最小化输出y2,y3,y4），Matlab完整源码

多目标优化|HKELM混合核极限学习机+NSGAII算法工艺参数优化、工程设计优化，四目标（最大化输出y1、最小化输出y2,y3,y4），Matlab完整源码

网友: 技术文档 2025-08-08 09:03:52

基本介绍

1.HKELM混合核极限学习机+NSGAII多目标优化算法，工艺参数优化、工程设计优化！（Matlab完整源码和数据）

多目标优化是指在优化问题中同时考虑多个目标的优化过程。在多目标优化中，通常存在多个冲突的目标，即改善一个目标可能会导致另一个目标的恶化。因此，多目标优化的目标是找到一组解，这组解在多个目标下都是最优的，而不是仅仅优化单一目标。
2.先通过HKELM混合核极限学习机封装因变量(y1 y2 y3 y4）与自变量(x1 x2 x3 x4 x5）代理模型，再通过nsga2寻找y极值（y1极大;y2 y3 y4极小），并给出对应的x1 x2 x3 x4 x5Pareto解集。

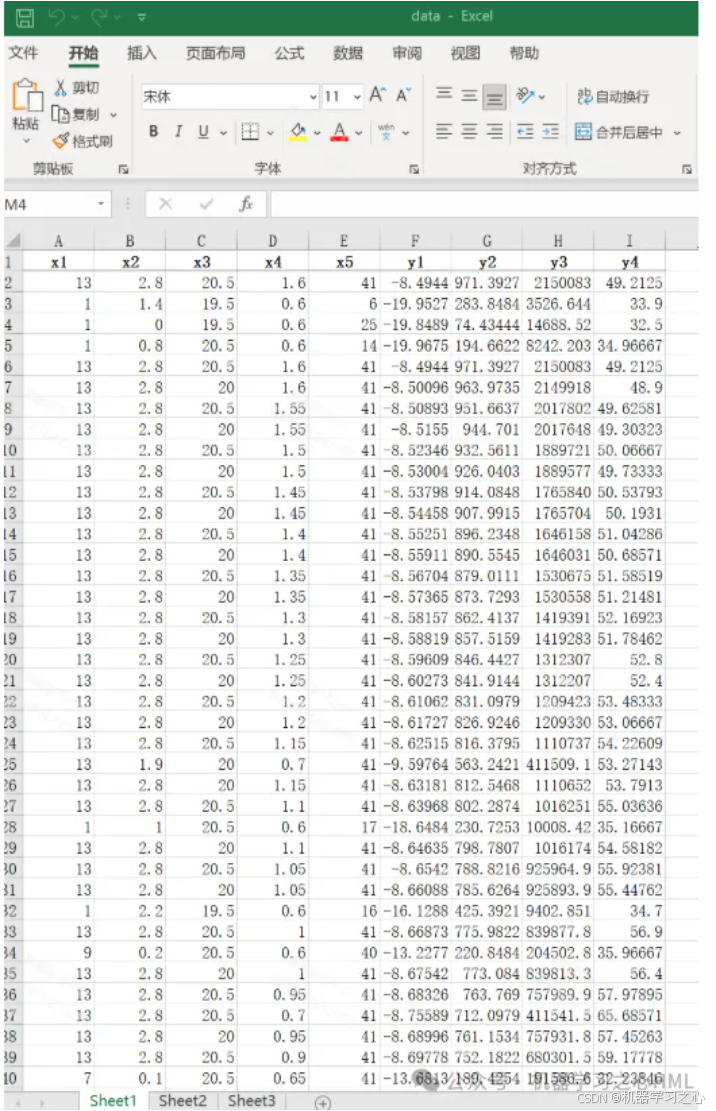
3.data为数据集，5个输入特征，4个输出变量，NSGAII算法寻极值，求出极值时(max y1; min y2;min y3;min y4)的自变量x1,x2,x3,x4,x5。

4.main1.m为HKELM混合核极限学习机主程序文件、main2.m为NSGAII多目标优化算法主程序文件，依次运行即可，其余为函数文件，无需运行。

5.命令窗口输出R2、MAE、MBE、MAPE、RMSE等评价指标，输出预测对比图、误差分析图、决定系数分析图、多目标优化算法求解Pareto解集图，可在下载区获取数据和程序内容。

6.适合工艺参数优化、工程设计优化等最优特征组合领域。

NSGA-II算法
1） 随机产生规模为N的初始种群Pt，经过非支配排序、 选择、 交叉和变异， 产生子代种群Qt， 并将两个种群联合在一起形成大小为2N的种群Rt；
2）进行快速非支配排序， 同时对每个非支配层中的个体进行拥挤度计算， 根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群Pt+1；
3） 通过遗传算法的基本操作产生新的子代种群Qt+1， 将Pt+1与Qt+1合并形成新的种群Rt， 重复以上操作， 直到满足程序结束的条件。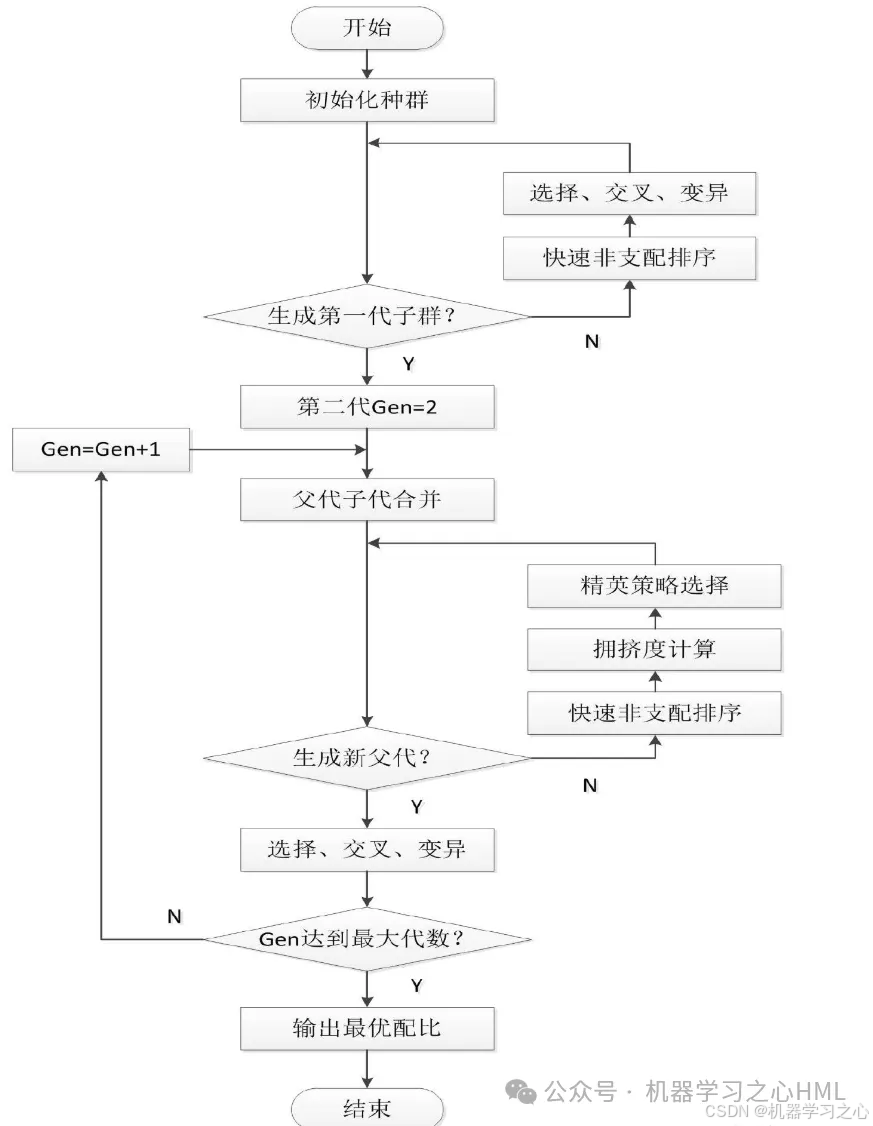
多目标优化|HKELM混合核极限学习机+NSGAII算法工艺参数优化、工程设计优化，四目标（最大化输出y1、最小化输出y2,y3,y4），Matlab完整源码

代码功能

main1_HKELM.m
  1. 核心功能：训练混合核极限学习机（HKELM）模型，用于多目标回归预测（4个输出）。
  2. 关键步骤：
    • 数据预处理：导入数据、划分训练/测试集（70%训练）、归一化。
    • HKELM建模：使用RBF+Poly双核函数组合，优化正则化系数和核参数。
    • 模型评估：计算RMSE、R²、MAE等指标，绘制预测结果对比图。
    • 模型保存：存储归一化参数、网络权重等至net.mat。
main2_NSGAII.m
  1. 核心功能：使用NSGA-II多目标优化算法，寻找使4个目标函数最优的输入变量组合。
  2. 优化目标：
    • 最大化输出1（y1）
    • 最小化输出2-4（y2,y3,y4）
  3. 关键步骤：
    • 初始化种群：定义5维输入变量范围和离散步长。
    • 多目标优化：通过非支配排序、拥挤度计算、遗传操作（交叉/变异）迭代进化。
    • 输出结果：Pareto最优解对应的输入变量和目标函数值。

逻辑关联

  1. 顺序依赖：
    • 必须先运行main1_HKELM.m生成net.mat模型文件。
    • main2_NSGAII.m的costfunction会加载此模型预测目标函数值。
  2. 数据流：#mermaid-svg-ErUGwDZ2RHjnan98 {font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-ErUGwDZ2RHjnan98 .error-icon{fill:#552222;}#mermaid-svg-ErUGwDZ2RHjnan98 .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-ErUGwDZ2RHjnan98 .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-ErUGwDZ2RHjnan98 .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-ErUGwDZ2RHjnan98 .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-ErUGwDZ2RHjnan98 .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-ErUGwDZ2RHjnan98 .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-ErUGwDZ2RHjnan98 .marker{fill:#333333;stroke:#333333;}#mermaid-svg-ErUGwDZ2RHjnan98 .marker.cross{stroke:#333333;}#mermaid-svg-ErUGwDZ2RHjnan98 svg{font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-ErUGwDZ2RHjnan98 .label{font-family:\"trebuchet ms\",verdana,arial,sans-serif;color:#333;}#mermaid-svg-ErUGwDZ2RHjnan98 .cluster-label text{fill:#333;}#mermaid-svg-ErUGwDZ2RHjnan98 .cluster-label span{color:#333;}#mermaid-svg-ErUGwDZ2RHjnan98 .label text,#mermaid-svg-ErUGwDZ2RHjnan98 span{fill:#333;color:#333;}#mermaid-svg-ErUGwDZ2RHjnan98 .node rect,#mermaid-svg-ErUGwDZ2RHjnan98 .node circle,#mermaid-svg-ErUGwDZ2RHjnan98 .node ellipse,#mermaid-svg-ErUGwDZ2RHjnan98 .node polygon,#mermaid-svg-ErUGwDZ2RHjnan98 .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-ErUGwDZ2RHjnan98 .node .label{text-align:center;}#mermaid-svg-ErUGwDZ2RHjnan98 .node.clickable{cursor:pointer;}#mermaid-svg-ErUGwDZ2RHjnan98 .arrowheadPath{fill:#333333;}#mermaid-svg-ErUGwDZ2RHjnan98 .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-ErUGwDZ2RHjnan98 .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-ErUGwDZ2RHjnan98 .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-ErUGwDZ2RHjnan98 .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-ErUGwDZ2RHjnan98 .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-ErUGwDZ2RHjnan98 .cluster text{fill:#333;}#mermaid-svg-ErUGwDZ2RHjnan98 .cluster span{color:#333;}#mermaid-svg-ErUGwDZ2RHjnan98 div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-ErUGwDZ2RHjnan98 :root{--mermaid-font-family:\"trebuchet ms\",verdana,arial,sans-serif;}保存模型加载模型main1_HKELMnet.matmain2_NSGAII预测y1-y4多目标优化

算法步骤与技术路线

HKELM（混合核极限学习机）
  1. 技术路线：#mermaid-svg-Xg3G1RpDQGQGWCty {font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-Xg3G1RpDQGQGWCty .error-icon{fill:#552222;}#mermaid-svg-Xg3G1RpDQGQGWCty .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-Xg3G1RpDQGQGWCty .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-Xg3G1RpDQGQGWCty .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-Xg3G1RpDQGQGWCty .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-Xg3G1RpDQGQGWCty .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-Xg3G1RpDQGQGWCty .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-Xg3G1RpDQGQGWCty .marker{fill:#333333;stroke:#333333;}#mermaid-svg-Xg3G1RpDQGQGWCty .marker.cross{stroke:#333333;}#mermaid-svg-Xg3G1RpDQGQGWCty svg{font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-Xg3G1RpDQGQGWCty .label{font-family:\"trebuchet ms\",verdana,arial,sans-serif;color:#333;}#mermaid-svg-Xg3G1RpDQGQGWCty .cluster-label text{fill:#333;}#mermaid-svg-Xg3G1RpDQGQGWCty .cluster-label span{color:#333;}#mermaid-svg-Xg3G1RpDQGQGWCty .label text,#mermaid-svg-Xg3G1RpDQGQGWCty span{fill:#333;color:#333;}#mermaid-svg-Xg3G1RpDQGQGWCty .node rect,#mermaid-svg-Xg3G1RpDQGQGWCty .node circle,#mermaid-svg-Xg3G1RpDQGQGWCty .node ellipse,#mermaid-svg-Xg3G1RpDQGQGWCty .node polygon,#mermaid-svg-Xg3G1RpDQGQGWCty .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-Xg3G1RpDQGQGWCty .node .label{text-align:center;}#mermaid-svg-Xg3G1RpDQGQGWCty .node.clickable{cursor:pointer;}#mermaid-svg-Xg3G1RpDQGQGWCty .arrowheadPath{fill:#333333;}#mermaid-svg-Xg3G1RpDQGQGWCty .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-Xg3G1RpDQGQGWCty .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-Xg3G1RpDQGQGWCty .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-Xg3G1RpDQGQGWCty .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-Xg3G1RpDQGQGWCty .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-Xg3G1RpDQGQGWCty .cluster text{fill:#333;}#mermaid-svg-Xg3G1RpDQGQGWCty .cluster span{color:#333;}#mermaid-svg-Xg3G1RpDQGQGWCty div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-Xg3G1RpDQGQGWCty :root{--mermaid-font-family:\"trebuchet ms\",verdana,arial,sans-serif;}数据预处理双核映射正则化求解输出权重预测+反归一化
  2. 核函数公式：
    • 混合核：K=ω⋅KRBF+(1−ω)⋅KPolyK = \\omega \\cdot K_{RBF} + (1-\\omega) \\cdot K_{Poly}K=ω⋅KRBF​+(1−ω)⋅KPoly​
    • RBF核：KRBF(xi,xj)=exp⁡(−∥xi−xj∥2σ2)K_{RBF}(x_i,x_j) = \\exp\\left(-\\frac{\\|x_i-x_j\\|^2}{\\sigma^2}\\right)KRBF​(xi​,xj​)=exp(−σ2∥xi​−xj​∥2​)
    • Poly核：KPoly(xi,xj)=(xi⋅xj+c)dK_{Poly}(x_i,x_j) = (x_i \\cdot x_j + c)^dKPoly​(xi​,xj​)=(xi​⋅xj​+c)d
  3. 参数设定：
    • Kernel_para = [σ, c, d, ω]（示例值：[0.001, 360, 5.0, 0.1]）
    • 正则化系数C=0.001
NSGA-II（非支配排序遗传算法）
  1. 优化流程：#mermaid-svg-UC7Y5Psgejhz5nl5 {font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-UC7Y5Psgejhz5nl5 .error-icon{fill:#552222;}#mermaid-svg-UC7Y5Psgejhz5nl5 .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-UC7Y5Psgejhz5nl5 .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-UC7Y5Psgejhz5nl5 .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-UC7Y5Psgejhz5nl5 .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-UC7Y5Psgejhz5nl5 .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-UC7Y5Psgejhz5nl5 .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-UC7Y5Psgejhz5nl5 .marker{fill:#333333;stroke:#333333;}#mermaid-svg-UC7Y5Psgejhz5nl5 .marker.cross{stroke:#333333;}#mermaid-svg-UC7Y5Psgejhz5nl5 svg{font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-UC7Y5Psgejhz5nl5 .label{font-family:\"trebuchet ms\",verdana,arial,sans-serif;color:#333;}#mermaid-svg-UC7Y5Psgejhz5nl5 .cluster-label text{fill:#333;}#mermaid-svg-UC7Y5Psgejhz5nl5 .cluster-label span{color:#333;}#mermaid-svg-UC7Y5Psgejhz5nl5 .label text,#mermaid-svg-UC7Y5Psgejhz5nl5 span{fill:#333;color:#333;}#mermaid-svg-UC7Y5Psgejhz5nl5 .node rect,#mermaid-svg-UC7Y5Psgejhz5nl5 .node circle,#mermaid-svg-UC7Y5Psgejhz5nl5 .node ellipse,#mermaid-svg-UC7Y5Psgejhz5nl5 .node polygon,#mermaid-svg-UC7Y5Psgejhz5nl5 .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-UC7Y5Psgejhz5nl5 .node .label{text-align:center;}#mermaid-svg-UC7Y5Psgejhz5nl5 .node.clickable{cursor:pointer;}#mermaid-svg-UC7Y5Psgejhz5nl5 .arrowheadPath{fill:#333333;}#mermaid-svg-UC7Y5Psgejhz5nl5 .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-UC7Y5Psgejhz5nl5 .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-UC7Y5Psgejhz5nl5 .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-UC7Y5Psgejhz5nl5 .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-UC7Y5Psgejhz5nl5 .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-UC7Y5Psgejhz5nl5 .cluster text{fill:#333;}#mermaid-svg-UC7Y5Psgejhz5nl5 .cluster span{color:#333;}#mermaid-svg-UC7Y5Psgejhz5nl5 div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:\"trebuchet ms\",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-UC7Y5Psgejhz5nl5 :root{--mermaid-font-family:\"trebuchet ms\",verdana,arial,sans-serif;}初始化种群非支配排序拥挤度计算选择+交叉+变异合并父代子代精英保留
  2. 关键公式：
    • 非支配排序：比较解之间的支配关系
    • 拥挤度：Id=∑m=1Mfm(i+1)−fm(i−1)fmmax⁡−fmmin⁡I_d = \\sum_{m=1}^M \\frac{f_m^{(i+1)} - f_m^{(i-1)}}{f_m^{\\max} - f_m^{\\min}}Id​=∑m=1M​fmmax​−fmmin​fm(i+1)​−fm(i−1)​​
  3. 参数设定：
    • 种群大小npop=50
    • 迭代次数maxit=100
    • 交叉概率pc=0.85, 变异概率mu=0.2
    • 变量范围：x1∈[1,13], x2∈[0,2.8], x3∈[3,21], x4∈[0.6,1.6], x5∈[6,41]

运行环境

  1. 依赖项：
    • MATLAB基础库
    • 自定义函数包：HKELM/ + NSGAII/
    • 数据文件：data.xlsx
  2. 硬件要求：
    • 无特殊要求（NSGA-II迭代100代属轻量级优化）

创新点总结

  1. 两阶段架构：
    • 阶段1：HKELM建立高精度代理模型（替代物理模型）
    • 阶段2：NSGA-II在代理模型上高效寻优
  2. 混合核优势：
    RBF核捕获局部特征 + Poly核描述全局趋势，提升回归泛化能力。
  3. 离散变量处理：
    create_x()函数实现带步长的离散变量生成（如x2步长0.1）。

注：完整运行需确保自定义函数包路径正确，且data.xlsx的格式与代码匹配（最后4列为输出）。

代码运行效果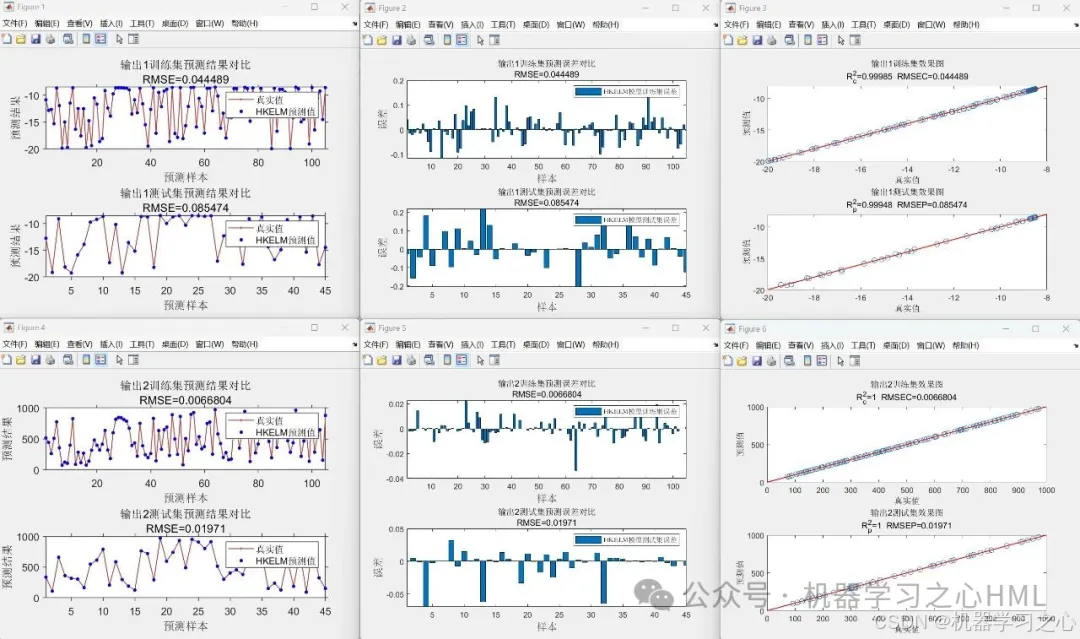
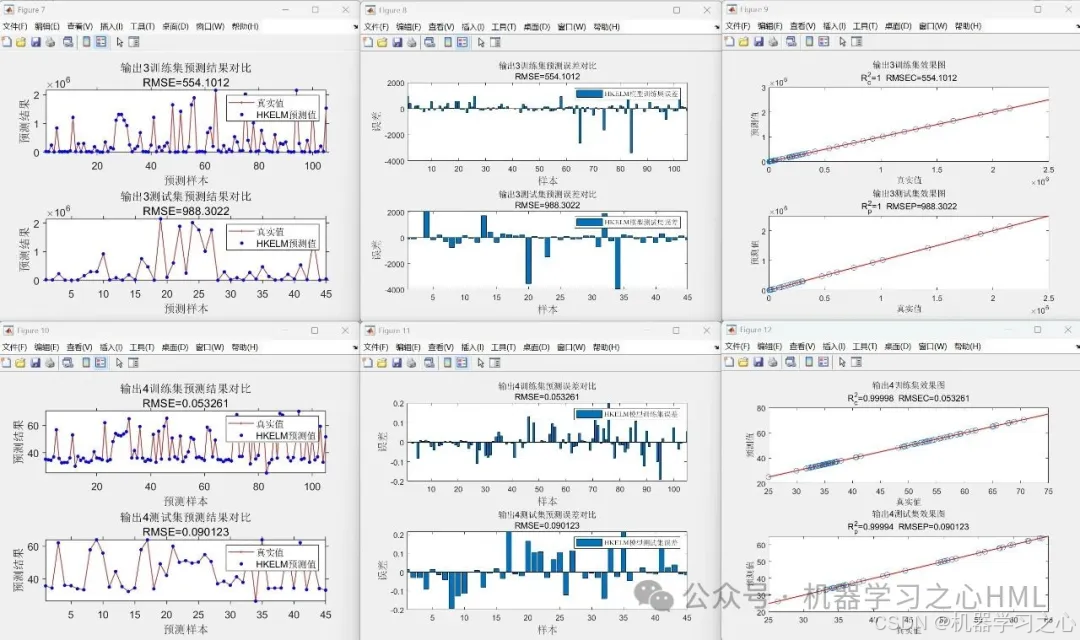
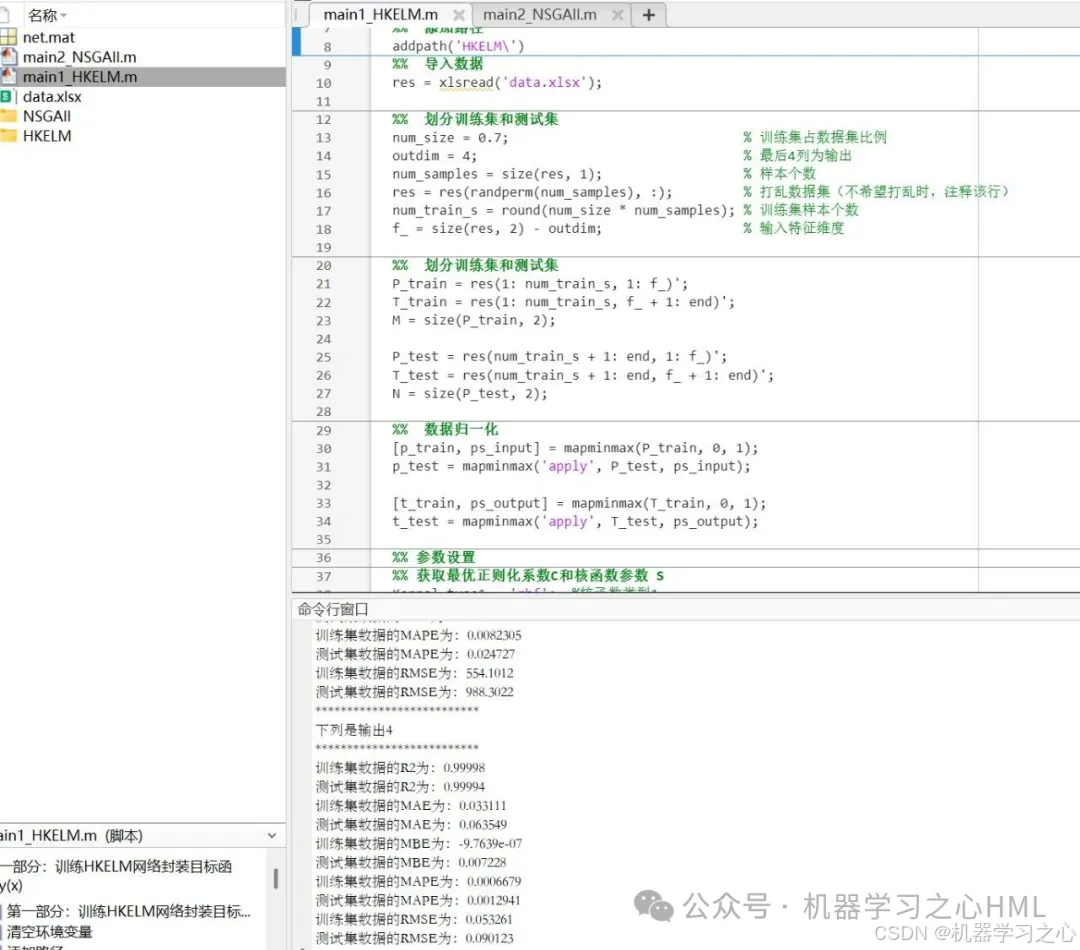
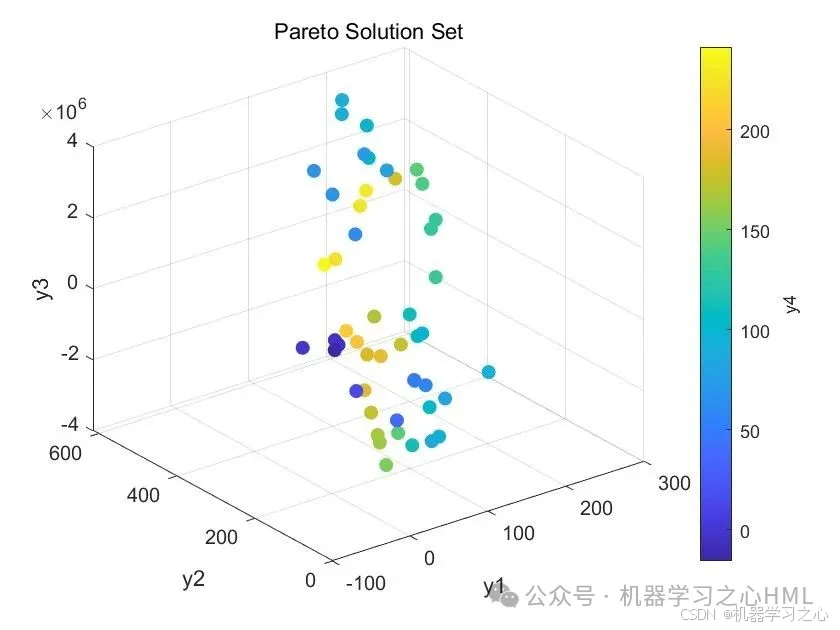
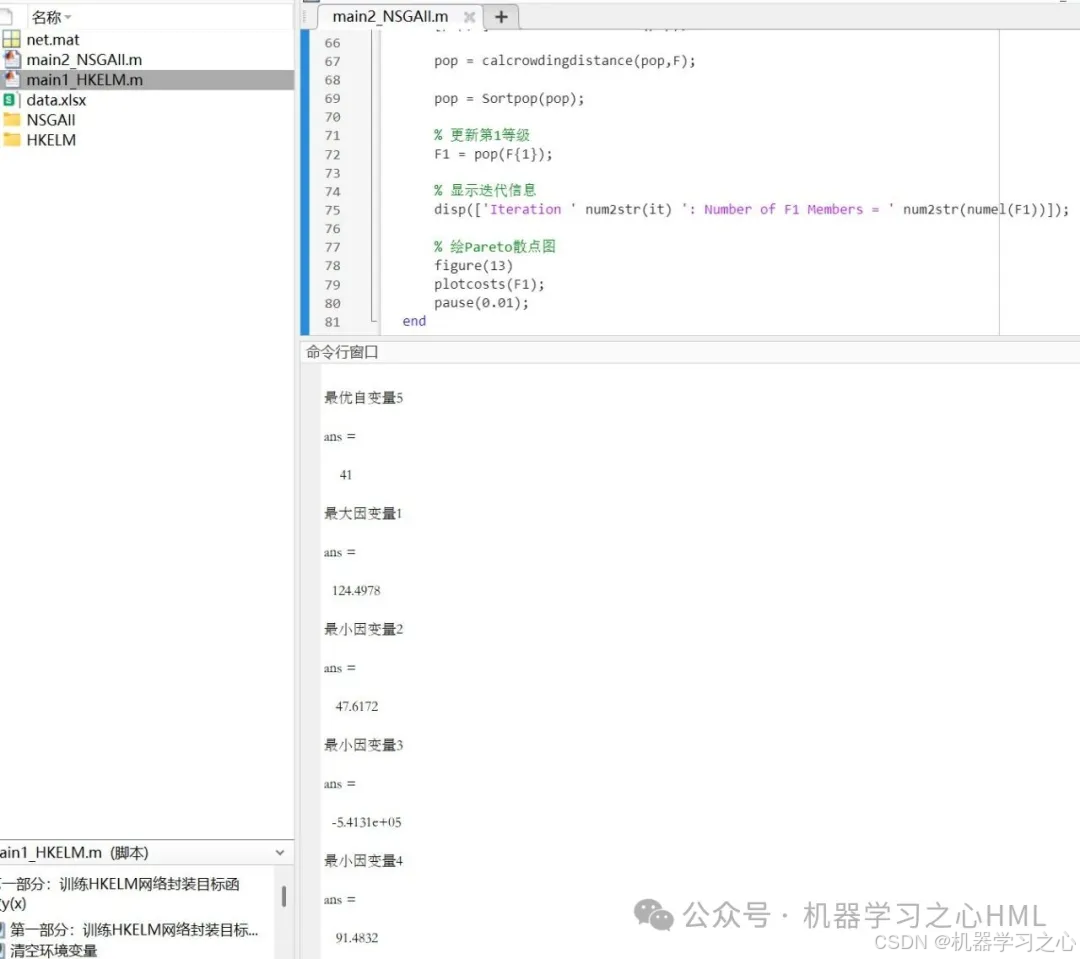
多目标优化|HKELM混合核极限学习机+NSGAII算法工艺参数优化、工程设计优化，四目标（最大化输出y1、最小化输出y2,y3,y4），Matlab完整源码
多目标优化|HKELM混合核极限学习机+NSGAII算法工艺参数优化、工程设计优化，四目标（最大化输出y1、最小化输出y2,y3,y4），Matlab完整源码
多目标优化|HKELM混合核极限学习机+NSGAII算法工艺参数优化、工程设计优化，四目标（最大化输出y1、最小化输出y2,y3,y4），Matlab完整源码
多目标优化|HKELM混合核极限学习机+NSGAII算法工艺参数优化、工程设计优化，四目标（最大化输出y1、最小化输出y2,y3,y4），Matlab完整源码
多目标优化|HKELM混合核极限学习机+NSGAII算法工艺参数优化、工程设计优化，四目标（最大化输出y1、最小化输出y2,y3,y4），Matlab完整源码
数据集
多目标优化|HKELM混合核极限学习机+NSGAII算法工艺参数优化、工程设计优化，四目标（最大化输出y1、最小化输出y2,y3,y4），Matlab完整源码

完整代码私信回复HKELM混合核极限学习机+NSGAII算法工艺参数优化、工程设计优化，四目标（最大化输出y1、最小化输出y2,y3,y4），Matlab完整源码

网络标签：

相关问题