【优选算法】双指针（一）

双指针

• 移动零
• 复写零
• 快乐数
• 盛最多水的容器

移动零

题目链接：移动零

题目描述：

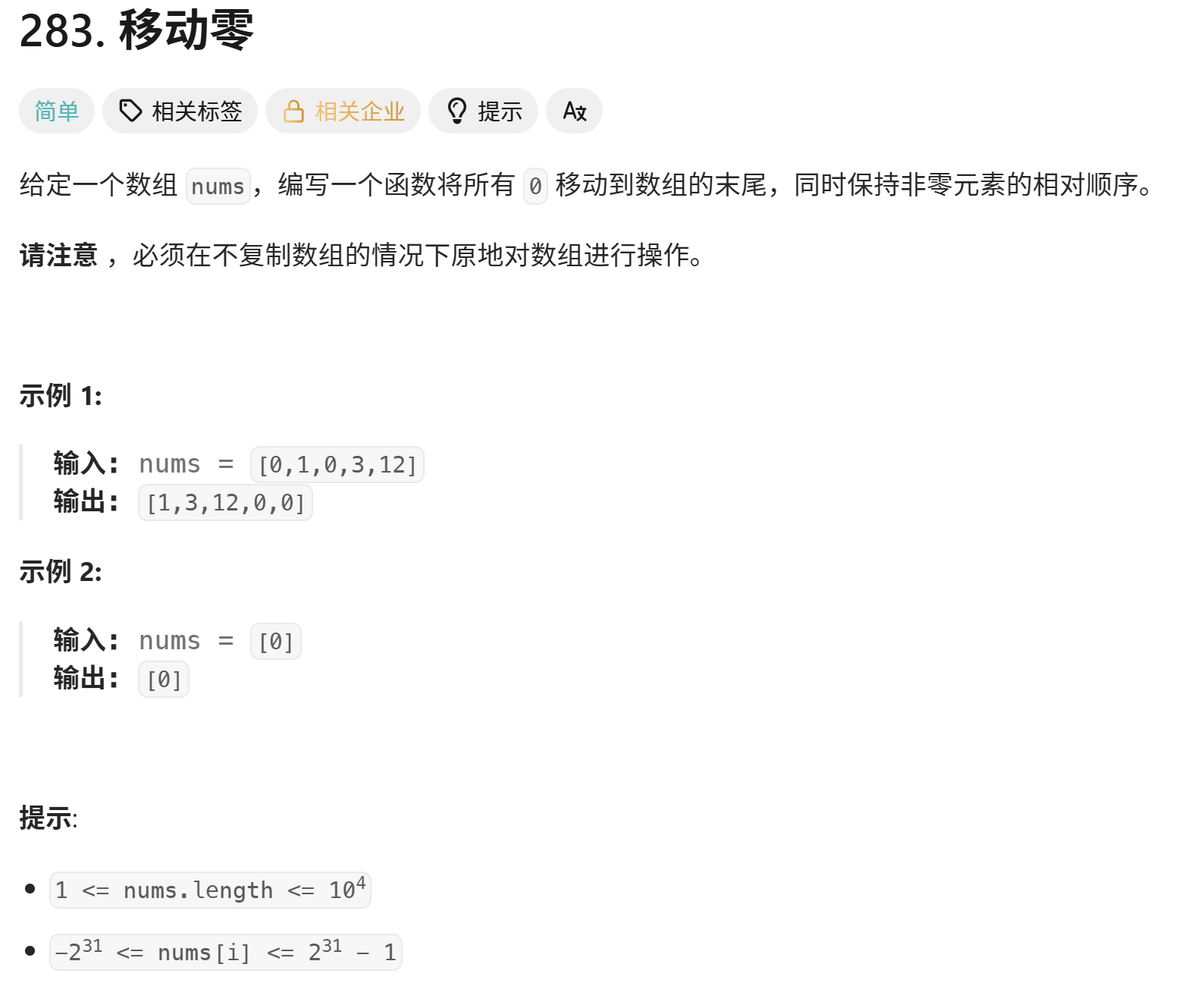
算法原理：

这种类型的题被称为【数组分块】，制定一种划分方式，将数组划分为若干个不同的区间。
解决这类题可以使用【双指针算法】：定义两个变量充当数组的下标以达到指针的效果。

双指针中两个指针的作用：
cur：从前往后扫描数组（未知区间）
dest：指向已处理区间的最后一个元素

两个指针把数组分成3个区间：
[0, dest] [dest + 1, cur - 1] [cur - 1, n - 1]

在本题中：
[0, dest] 指的是非零区间
[dest + 1, cur - 1] 指的是全零区间
[cur, n - 1] 指的是待扫描区间

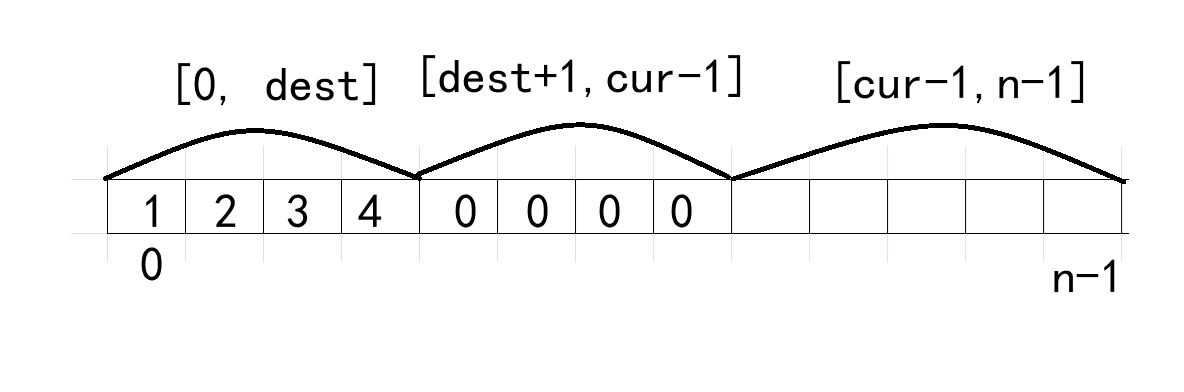
初始化时cur = 0,dest = -1,此时还未扫描，所以dest指向首元素的前一个位置。

cur在从前向后扫描的过程中：

1. 遇到 0 元素，++cur
2. 遇到非零元素，swap(nums[++dest], nums[cur++])

代码：

class Solution {public: void moveZeroes(vector<int>& nums) { for(int cur = 0, dest = -1; cur < nums.size(); ++cur) if(nums[cur]) swap(nums[++dest], nums[cur]); }};

复写零

题目链接：复写零

题目描述：

算法原理：

利用双指针，在原始数组上解决问题。

先利用双指针通过“异地操作”寻找优化成“原地操作”的方法

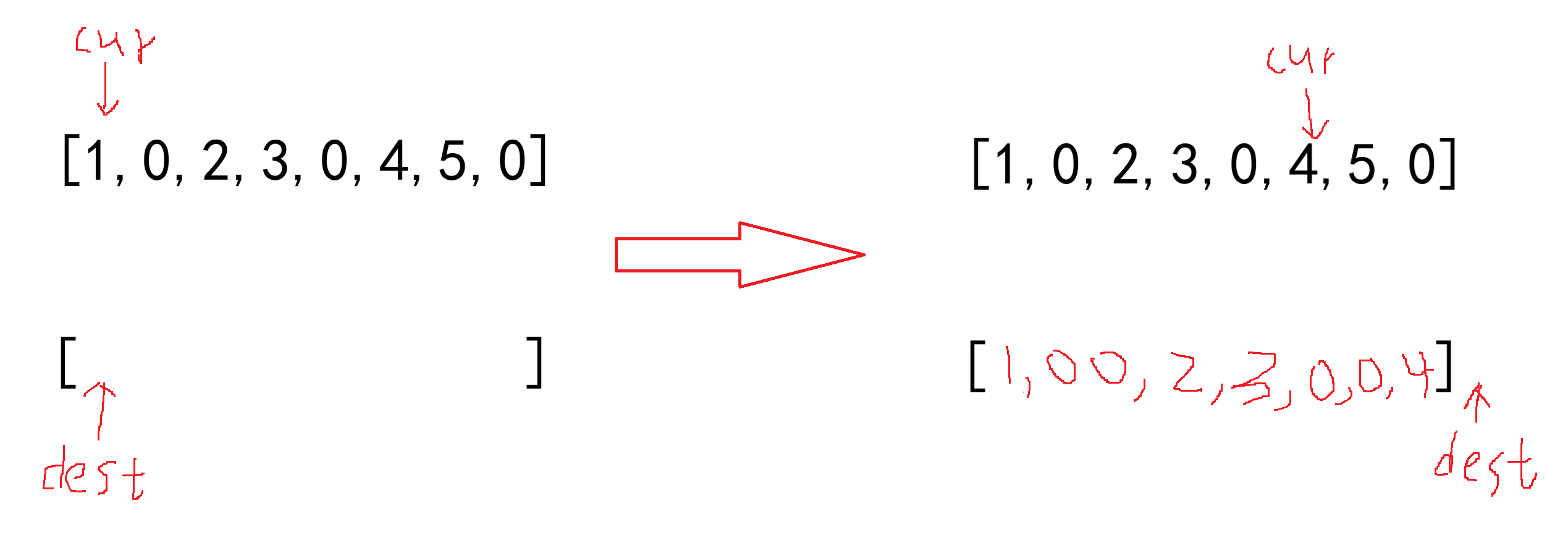
利用双指针在原数组上从前往后遍历，发现dest会跑到cur的后面，所以不能从前往后遍历。

试一试从后往前遍历，发现是可以的，但要确定 cur 的起始位置

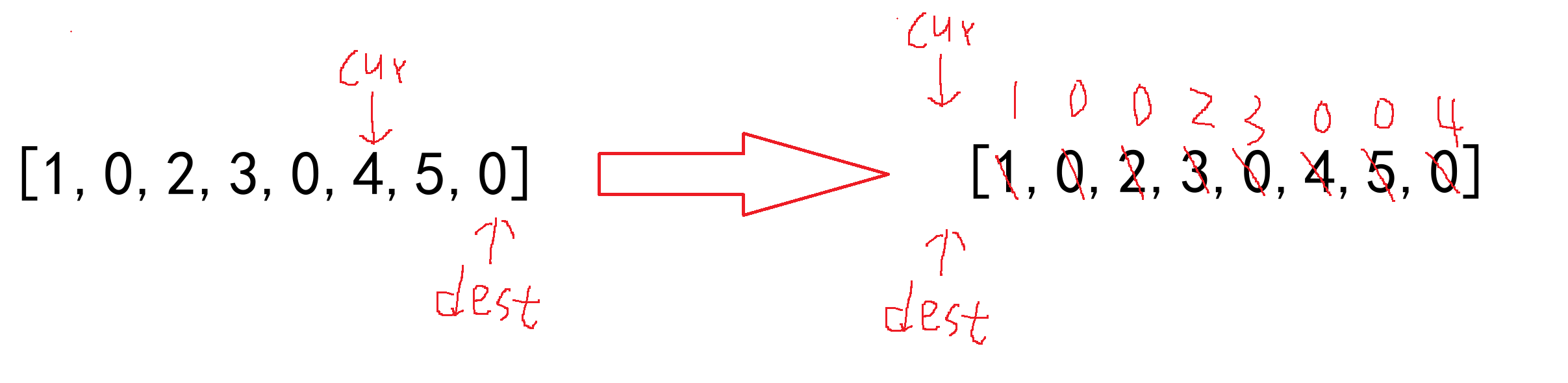
总结：
1. 找到最后一个要“复写”的数的位置
此时可以在双指针中再套一个双指针，以便后续的复写操作

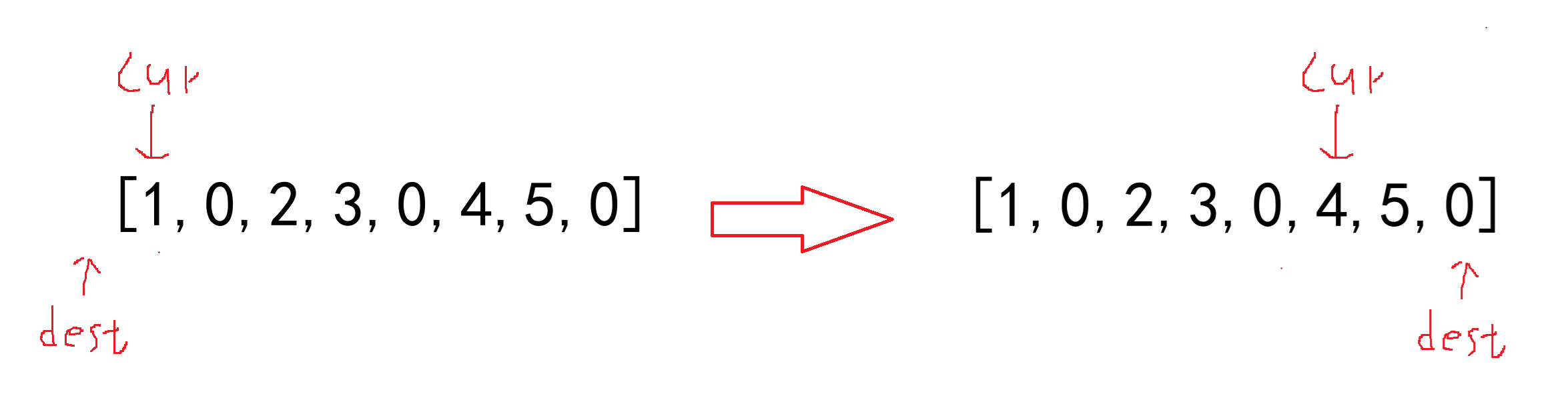
1. 判断 cur 位置的值
2. 根据其是否为 0 ，决定 dest 要向后走一步还是两步
3. 判断 dest 位置
4. 根据其是否在最后一个位置之前，决定是否++cur
5. 循环条件 dest < n - 1

2. 处理边界情况

边界情况出现的原因：最后一个要“复写”的数是 0 ，导致 dest 走了两步使 dest == n

解决方法：
arr[n - 1] = 0;
dest -= 2;
–cur;

3. 从后往前完成复写操作

1. 如果 cur 位置的值不为 0
   arr[dest–] = arr[cur–];
2. 如果 cur 位置的值为 0
   arr[dest–] = arr[cur];
   arr[dest–] = arr[cur–];
3. 循环条件：cur >= 0

代码：

class Solution {public: void duplicateZeros(vector<int>& arr) { // 1. 找到最后一个要“复写”的数的位置 int dest = -1, cur = 0, n = arr.size(); while(dest < n - 1) { if(arr[cur]) ++dest; else dest += 2; if(dest < n - 1) ++cur; } // 2. 处理边界情况 if(dest == n) { arr[n - 1] = 0; dest -= 2; --cur; } // 3. 从后往前完成复写操作 while(cur >= 0) { if(arr[cur]) arr[dest--] = arr[cur--]; else { arr[dest--] = arr[cur]; arr[dest--] = arr[cur--]; } } }};

快乐数

题目链接：快乐数

题目描述：

题目解析

对于示例一：19 -> 82 -> 68 -> 100 -> 1 之后就是 1 循环
对于示例二：2 -> 4 -> 16 -> 37 -> 58 -> 89 -> 145 -> 42 -> 20 -> 4 之后就是循环该过程

这两个实例刚好符合题目中给的两种情况

1. 情况一：一直死循环 1
2. 情况二： 一直死循环 一些数，始终变不到 1

扩展了解

其实如果题目不给这个提示的话，我们在思考的过程中是会有第三种情况的，
也就是不会进入到循环的情况，我们可以证明该情况是不存在的

证明过程

1. 由数据范围知最大值为2^31 - 1 = 2147483647，为了方便计算我们将其扩大为9999999999，
   经过一次平方和操作后变为：9^2 * 10 = 810，也就是变化区间为[1, 810]。
2. 根据雀巢原理：经过 811次平方和操作后，必然会形成一个环。
3. 所以不会进入到循环的情况是不存在的

算法原理：

如果学过数据结构的链表的话，那应该会做过判断链表是否有环，用快慢指针解决

该题也可以用快慢指针解决，只不过这里的 fast 和 slow 是指向一个一个数

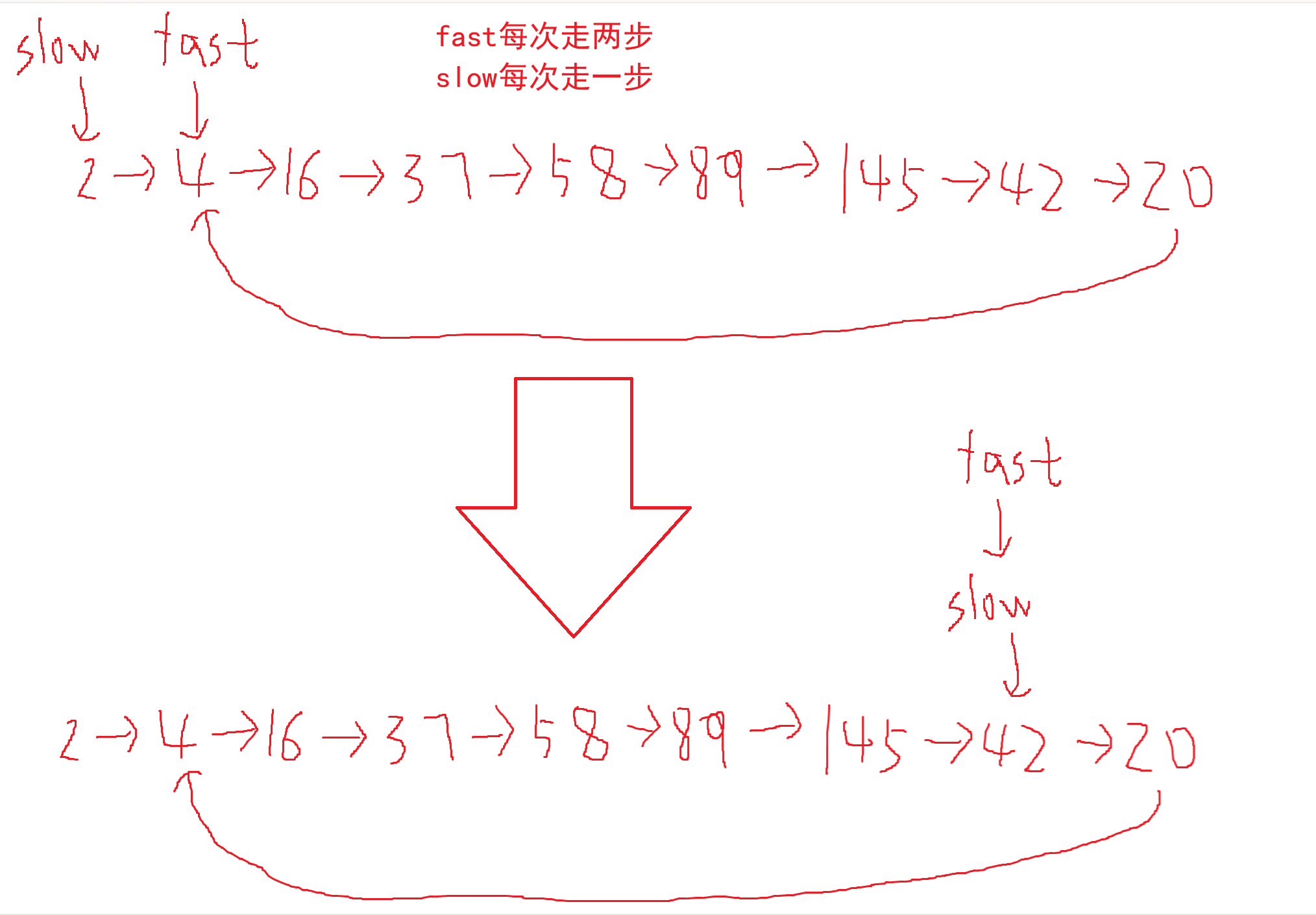
1. 定义快慢指针
2. 慢指针每次走一步，快指针每次走两步
3. 判断相遇时的值是否为 1

代码：

class Solution {public: int bitSum(int n) // 返回 n 这个数每一位的平方和 { int sum = 0; while(n) { int t = n % 10; sum += t * t; n /= 10; } return sum; } bool isHappy(int n) { int slow = n, fast = bitSum(n); while(slow != fast) { slow = bitSum(slow); fast = bitSum(bitSum(fast)); } return slow == 1; }};

盛最多水的容器

题目链接：盛最多水的容器

题目描述：

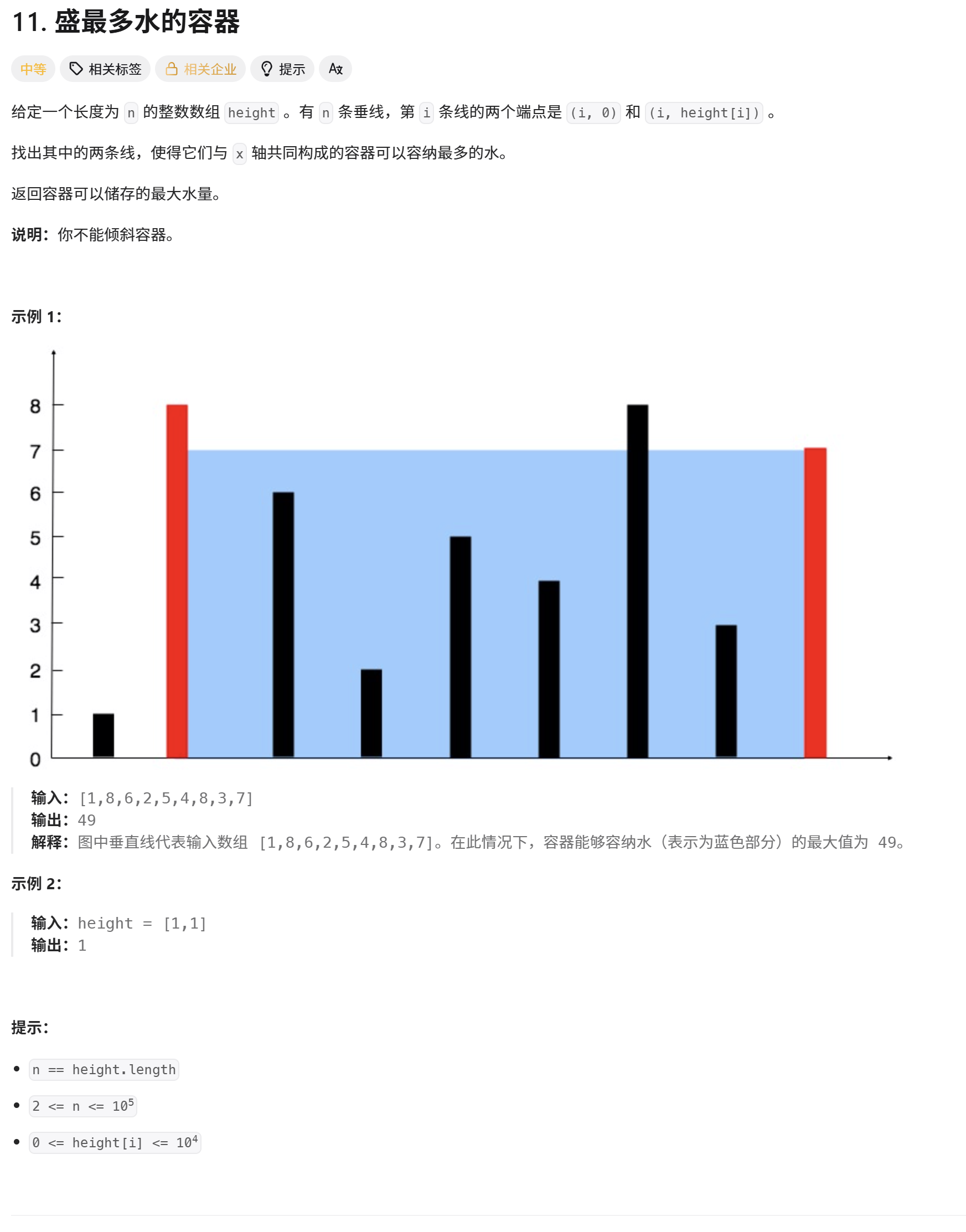
题目解析

算法原理：

代码：

class Solution {public: int maxArea(vector<int>& height) { int left = 0, right = height.size() - 1; int ret = 0; while(left < right) { int v = (right - left) * min(height[left], height[right]); ret = max(ret, v); if(height[left] < height[right]) ++left; else --right; } return ret; }};