不同数据类型在内存中的存储——深入理解内存数据结构

数据在内存中的存储方式会因数据类型的不同而有所差异，本文将围绕几种常见的数据类型展开进行分析，了解这些数据类型在内存中的存储，可以更好地帮助我们理解内存的数据结构，掌握数据在内存中的存储方式，对内存中的数据有更直观的认识。内存中的数据以小端存储方式较为常见，即低位数据存放在低地址，高位数据存放在高地址，下面的数据也是建立在小端存储的情况下进行存储，我们将数据分为两大类，整数和浮点数，来进行展开分析。

一、整数在内存中的存储

（1）int型数据：

整形数据在内存中均以二进制的形式存储，int型数据在内存中占4个字节，一个字节为8个比特位，故全部为32个比特位，每个比特位存放0或者1这两个数字，低位数据存放在低地址，高位数据存放在高地址，整形数据的最低位的地址即为整型数据的地址，整型数据内部也分为有符号整形和无符号整形，有符号整形数据中，符号位为最高位，1表示负，0表示正，不难得出，无符号整形数据能表示的最大整数为有符号整数数据的两倍。

（2）char型数据：

char类型数据在内存中的存储可以说是建立在整形数据的基础上，存储方式与整形数据类似，但char类型数据在内存中只存储1个字节，与等值的整形数据相比，只取该整形数据的最后低八位，存储在内存中。

如上图，定义了一个char类型的数据ch=1，若1为整型数据，则在内存中的存储为00000000 00000000 00000000 00000001，而char类型只取整形最后低八位00000001存储在内存中，故char类型的数据1在内存中的存储为00000001。char类型数据同样也分为有符号型和无符号型，无符号char型数据能表示的最大整数同样为有符号char型数据的两倍。同样，有符号char型数据中，最高位为符号位，但char类型的数据能表示的数的范围远远小于整形数据，由于char在内存只存储1个字节，即8个比特位，在有符号char型数据中，最大数为01111111，即127，最小10000000，即-128，故有符号char类型的数据的取值范围为-128~127，无符号char型数据能表示的最大整数为有符号char型数据的两倍，易知，无符号char型数据的取值范围0~255。有了这个认识后，我们来看下面这个例子:

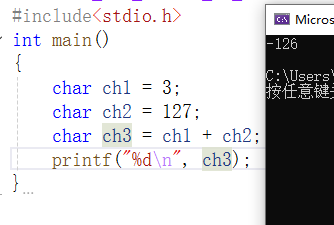
3与127的和为130，存放在ch3中，为什么ch3的值为-126呢？原因在于130超出了char类型数据所能表示的最大数127，发生溢出，130在char中的数据为10000010，10000010在有符号char类型中，由于最高位为1，即符号位为1，表示负数，负数在内存表示形式为补码，对10000010进行取反加一，得到原码11111110，即为-126，因此ch3的值为-126。

由上图可知，130存放在char类型中表示的值为-126，,进一步思考可知，当char类型数据发生溢出时，例如128存放在char中，结合上面的补码转化，可知128存放在char类型中表示的值为-128，同理，129在char中的值为-127,131在char中的值为-125，......，可知char类型数据是个循环数列，从0~127,128就变为-128,129变为-127,130变为-126，以此类推，255变为-1,256变为0，为一个循环，0~127，-128~0。至此，我们就可以尝试解决下面这个问题了。

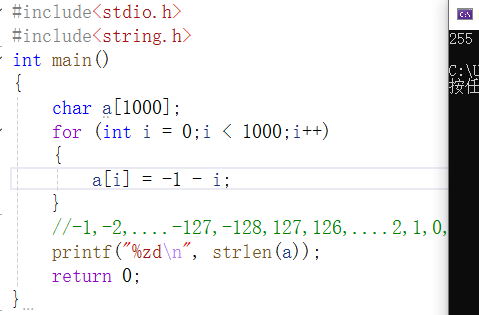
这里定义了一个char类型的数组，利用for循环对数组进行赋值，strlen函数求数组a的长度，可知当赋值到a[127]时，a[127]的值为-128，则a[128]的值为127，....随后递减为0，ASCII码为0的字符表示‘\\0’，读取到‘\\0’时，strlen停止计数，\'\\0\'之前有255个字符，故strlen函数所求结果为255。

二、浮点数在内存中的存储

浮点数在内存中也是以32位二进制的形式进行存储，但其存储方式与整数在内存中的存储方式却截然不同，浮点数存储采用IEEE754标准，这里我们以单精度float类型的浮点数为代表，具体分析下float类型浮点数在内存中的存储方式。

首先，要认识三个参数，S,M,E,S用于-1的S次幂，表示该浮点数的正负，浮点数为正时，S=0,浮点数为负时，S=1,E用于2的E次幂，M+1与前面两者相乘的结果即为该浮点数，浮点数在内存中的存储也就是这3个参数在内存中的存储。因此，为了实现浮点数在内存中的存储，要先将浮点型数据转化为以2为底数的科学计数法形式，进而计算出S,M,E，然后S存放在最高位，E+127的值存放在紧跟S之后的中间8位，M存放在最后23位，若M位数不够，则用0补足剩余的位数，浮点数的存储就完成了，此外，当E+127的8位全为0时，此时规定E的值为-126，可知，该浮点数的值非常小，趋近于0。

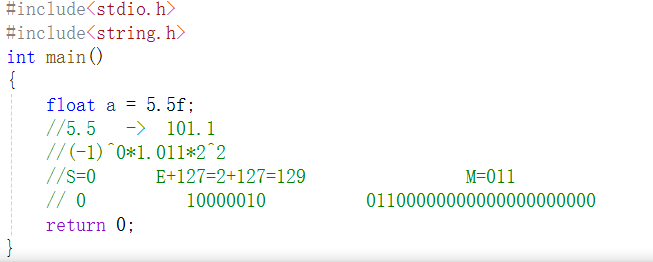
以5.5为例，首先现将5.5转化为以2为底数的科学计数法形式，进而求得S=0,E+127=2+127=129,M=011。

再将S,E+127,M以32位二进制的形式存放在内存中，如上图，则浮点数5.5在数据中的存储内容为

01000001001100000000000000000000,。

再看下面这个例子

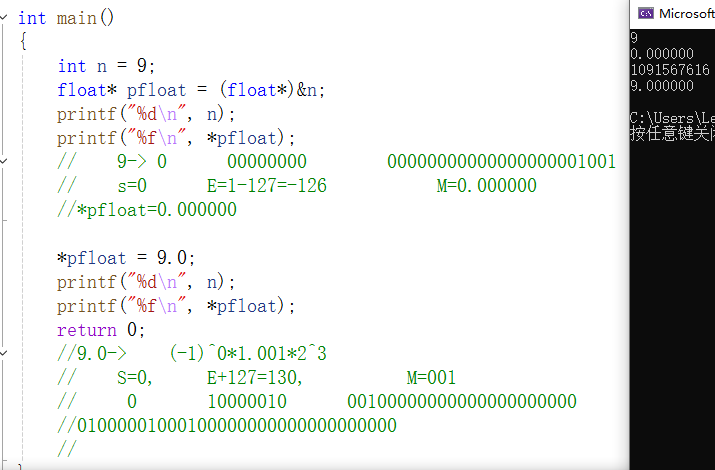
首先，定义了一个整形变量n的值为9，然后将n的地址强制类型转化为float类型，最后对float类型n的地址解引用，结果为0.000000，而不是9，为什么呢？这就是由于整形数据与浮点数数据在内存中的存储方式不同导致的，以float的视角看整形数据9在内存中的存储时，可得S=0,此时E+127的8位全为0，则E=1-127=126，则此时该浮点数非常小，可以认为是0，结果保留6位小数，则结果为0.000000。

第二个则与第一个刚好相反，9.0为float类型，首先把9转化为以2为底数的科学计数法形式，求得S=0,E+127=3+127=130，M=001，然后将S,E+127,M以32位二进制形式存放在内存中，结果为

01000001000100000000000000000000，再以整形数据的视角看待该32位二进制序列，值为一个很大的数字，为1091567616。

总结

在计算机中，数据的存储方式直接影响程序的运行结果，本文我们深入探讨了不同数据类型char，int，浮点数在内存中的存储方式，并分析了数据溢出，大小端存储，补码表示等相关概念。理解数据存储机制，不仅能帮助我们排查诡异的Bug，还能优化程序性能，当我们下次遇到数值突然变负或者浮点数计算不精确的情况时，不妨尝试从内存数据的存储角度进行分析，或许就能找到答案！