C++ 容器适配器与核心数据结构精解：栈、队列、deque 底层实现与实战应用----《Hello C++ Wrold!》(17)--(C/C++)

文章目录

• 前言
• stack
• • 其中常用的接口
  • stack的模拟实现
• queue
• • 其中常见的接口
  • queue的模拟实现
• deque
• • 常见接口
• 容器适配器
• priority_queue
• • 常用接口
  • priority_queue模拟实现
• 反向迭代器的模拟实现
• 仿函数(又叫函数对象)
• 作业部分
• • 逆波兰表达式
  • 引申

前言

在 C++ 标准库的庞大体系中，数据结构是支撑高效编程的基石，而容器适配器、序列容器以及相关的算法逻辑，则是其中最具实用价值的核心内容。无论是日常开发还是算法刷题，栈（stack）、队列（queue）、优先级队列（priority_queue）这些 “常客” 的身影几乎无处不在，它们看似简单的接口背后，藏着对数据存取规则的精妙设计 —— 栈的 “先进后出” 适配递归调用、括号匹配等场景，队列的 “先进先出” 适配层序遍历、任务调度等需求，优先级队列则通过堆结构实现带权重的数据筛选，成为 TopK 问题的利器。

深入学习这些结构时，我们往往会产生更多疑问：为什么栈和队列的默认底层容器是 deque 而非 vector 或 list？deque 的 “分段连续” 存储到底特殊在哪里，能同时兼顾头尾操作效率与一定的随机访问能力？优先级队列中，仿函数（函数对象）是如何灵活控制堆的排序逻辑的？反向迭代器的设计又暗藏哪些技巧，能让遍历方向反转却不影响底层数据结构？这些问题的答案，恰恰是从 “会用” 到 “精通” 的关键。

本文不仅会系统梳理栈、队列、deque、优先级队列的核心接口与使用场景，更会通过完整的模拟实现代码，拆解容器适配器的封装逻辑 —— 比如栈如何基于 deque 的尾插尾删实现 “先进后出”，优先级队列如何通过向上 / 向下调整算法维护堆结构。同时，针对仿函数、反向迭代器等容易混淆的概念，我们会结合实例解析其原理与应用，帮你理清 “less 与 greater 的区别”“反向迭代器的 ++ 为何是底层迭代器的 --” 等细节。

理论之外，实战更能检验掌握程度。文中精选了力扣（如最小栈、二叉树层序遍历、数组第 K 大元素）和牛客网（如栈的压入弹出序列）的经典题目，不仅提供解题思路，更附上完整代码实现，让你在刷题中直观感受容器的妙用。此外，针对容器特性的选择题解析（如不同容器迭代器的失效问题、deque 与 vector 的区别），能帮你规避学习中的常见误区。

无论你是刚接触 C++ 容器的初学者，还是想夯实数据结构基础的进阶者，这篇内容都能为你搭建一条从底层原理到实战应用的清晰路径。吃透这些知识，不仅能让你在面对复杂问题时快速找到数据结构选型的最优解，更能培养对代码逻辑的深层理解 —— 毕竟，真正的编程能力，从来都藏在对 “为什么这样设计” 的追问与探索中。

stack

栈的话是先进后出

注意区分栈顶和栈底–栈顶是最后放入的那个

其中常用的接口

empty() size() top() push(val) pop()

–注意:没有迭代器 不要去访问空的栈–可能有未定义行为

栈的构造:

eg:stackst;

stack的模拟实现

namespace renshen{// 容器适配器template<class T, class Container = deque<T>>class stack{public:void push(const T& x){_con.push_back(x);}void pop(){_con.pop_back();}T& top(){return _con.back();}size_t size(){return _con.size();}bool empty(){return _con.empty();}private:Container _con;};//补充:queue和stack库里面也有容器适配器

queue

队列的话是先进先出

其中常见的接口

empty() size() front() back() push(val) pop()

–也没有迭代器

队列的构造:

eg: queuea;

queue的模拟实现

namespace renshen{// 容器适配器template<class T, class Container = deque<T>>class queue{public:void push(const T& x){_con.push_back(x);}void pop(){_con.pop_front();}T& front(){return _con.front();}T& back(){return _con.back();}size_t size(){return _con.size();}bool empty(){return _con.empty();}private:Container _con;};//引申:vector和list都有front和back

deque

相比于vector:

1.deque极大缓解了扩容问题和能头插头删

2.deque的[]不太行，随机访问太慢了

相比于list:

1.deque支持下标随机访问

2.dequecpu高速缓存的效率不错

3.list的中间插入比deque好很多

总结:deque适合高频头插头删，尾插尾删；并且需要少量下标随机访问

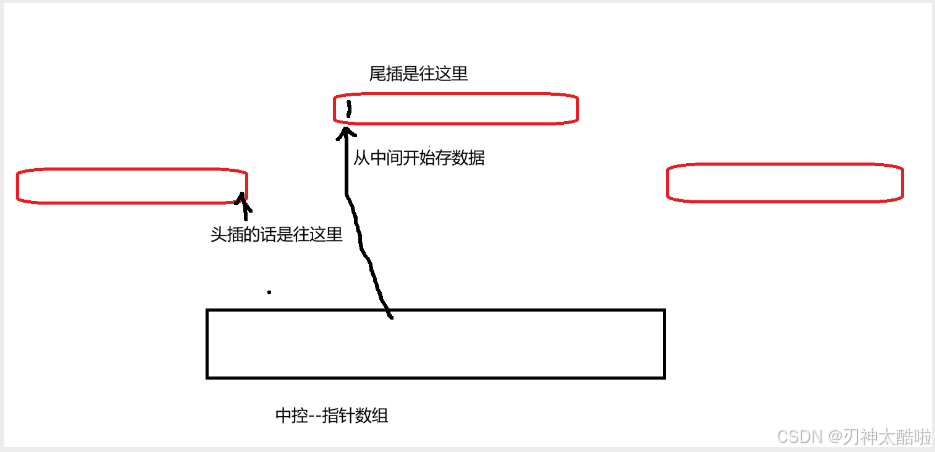
deque的模拟实现用的是中控指针数组(控制的是分散的一片一片区域[不是一个一个数据])

中控指针数组满了的话，扩下容就可以了

关于他的[]的模拟写法:([i])1.先看再不在第一个数组里面,.....2.不在就i-第一个数组的size 然后看再哪个数组里面就行了

常见接口

begin end rbegin rend size empty resize [] front back erase clearpush_front push_back pop_front pop_back insert

容器适配器

取名一般都是用的container 让模板能具有

priority_queue

叫做优先级队列，其实就是堆（堆顶就是最上面那个）

上面是类模板定义--可以看出，默认是大堆用法eg:priority_queue<int,vector,greater> pq引申：greater和greater()区分，一个是函数模板，一个是类模板

这个是构造函数的声明

topk问题的话用堆排序好些，全排序的话还是sort 时间复杂度是nlogn

常用接口

empty size top push(push进去自动排) pop(pop的最顶上那个)--没有迭代器--遍历的话只能逐项走过去

priority_queue模拟实现

namespace renshen{template<class T, class Container = vector<T>, class Comapre = less<T>>class priority_queue{private:void AdjustDown(int parent){Comapre com;size_t child = parent * 2 + 1;while (child < _con.size()){if (child + 1 < _con.size() && com(_con[child],_con[child + 1])){++child;}if (com(_con[parent],_con[child])){swap(_con[child], _con[parent]);parent = child;child = parent * 2 + 1;}else break;}}void AdjustUp(int child){Comapre com;int parent = (child - 1) / 2;while (child > 0){if (com(_con[parent],_con[child])){swap(_con[child], _con[parent]);child = parent;parent = (child - 1) / 2;}else break;}}public:priority_queue(){}template<class InputIterator>priority_queue(InputIterator first, InputIterator last){while (first != last){_con.push_back(*first);++first;}// 建堆for (int i = (_con.size()-1-1)/2; i >= 0; i--){AdjustDown(i);}}void pop(){swap(_con[0], _con[_con.size() - 1]);_con.pop_back();AdjustDown(0);}void push(const T& x){_con.push_back(x);AdjustUp(_con.size() - 1);}const T& top(){return _con[0];}bool empty(){return _con.empty();}size_t size(){return _con.size();}private:Container _con;};

反向迭代器的模拟实现

rbegin其实是end位置,rend其实是begin位置(rbegin并不是最后一个有元素的那个位置！)

namespace renshen{template<class Iterator, class Ref, class Ptr>struct ReverseIterator{typedef ReverseIterator<Iterator, Ref, Ptr> Self;Iterator _it;ReverseIterator(Iterator it):_it(it){}Ref operator*(){Iterator tmp = _it;return *(--tmp);}//反向迭代器解引用的是前一个位置Ptr operator->(){return &(operator*());}//引申:编译器会自动用返回的指针做 -> 操作Self& operator++(){--_it;return *this;}Self& operator--(){++_it;return *this;}bool operator!=(const Self& s) const{return _it != s._it;}};}

引申:重载运算符的结合性和优先级是跟本身的运算符一样的

仿函数(又叫函数对象)

这个类对象可以像函数一样使用

eg:template<class T>class Less{public:bool operator()(const T& x, const T& y){return x < y;}};调用方法:Less lesstest;lesstest(1,2)或者lesstest.operator()(1,2)

引申:库里面的less<T>是用来搞升序的,greater<T>是用来搞降序的

作业部分

力扣 155. 最小栈

力扣 最小栈注意:那个题能用容器来做！做法:搞两个栈，有一个用来存最小值(_min)--插入比当前<=的就放进去--pop出的值跟_min栈顶一样的话就_min也pop

代码展示:class MinStack {public:  void push(int val) { _st.push(val); if(_min.empty()||val<=_min.top()) _min.push(val); } void pop() { if(_st.top() == _min.top()) _min.pop(); _st.pop(); } int top() { return _st.top(); } int getMin() { return _min.top(); } private: stack<int>_st; stack<int>_min;};/** * Your MinStack object will be instantiated and called as such: * MinStack* obj = new MinStack(); * obj->push(val); * obj->pop(); * int param_3 = obj->top(); * int param_4 = obj->getMin(); */

牛客网 栈的弹出压入序列

牛客网 栈的弹出压入序列做法: 栈没跟出栈序列的元素匹配就入数据，匹配了的话就出数据--全入完了栈里面还有数据就说明不对

class Solution { public: /** * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可 * * * @param pushV int整型vector * @param popV int整型vector * @return bool布尔型 */ bool IsPopOrder(vector<int>& pushV, vector<int>& popV) { // write code here stack<int> st; int pushi = 0; int popi = 0; while (pushi <= pushV.size() - 1) { st.push(pushV[pushi++]); while (!st.empty() && st.top() == popV[popi]) { popi++; st.pop(); } } return popi == pushi; }};

力扣 102. 二叉树的层序遍历
107. 二叉树的层序遍历 II

力扣 102. 二叉树的层序遍历
做法:用queue 但是要注意root为空的情况

107. 二叉树的层序遍历 II
     做法:就是在上一题的答案的基础上，reverse一下就行(因为这个题要求自底向上遍历)

力扣 102. 二叉树的层序遍历的代码展示:/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */class Solution {public: vector<vector<int>> levelOrder(TreeNode* root) { vector<vector<int>>vv; queue<TreeNode*>q; int levelsize = 0; if(root) { q.push(root); levelsize = 1; }  while(!q.empty()) { vector<int> v; for(int i = 1;i<=levelsize;i++) { TreeNode* j = q.front(); q.pop(); v.push_back(j->val); if(j->left) q.push(j->left); if(j->right) q.push(j->right); } levelsize = q.size(); vv.push_back(v); } return vv; }};

107. 二叉树的层序遍历 II的代码展示:/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */class Solution {public: vector<vector<int>> levelOrderBottom(TreeNode* root) { vector<vector<int>>vv; queue<TreeNode*>q; int levelsize = 0; if(root) { q.push(root); levelsize = 1; }  while(!q.empty()) { vector<int> v; for(int i = 1;i<=levelsize;i++) { TreeNode* j = q.front(); q.pop(); v.push_back(j->val); if(j->left) q.push(j->left); if(j->right) q.push(j->right); } levelsize = q.size(); vv.push_back(v); } reverse(vv.begin(),vv.end()); return vv; }};

力扣 215. 数组中的第K个最大元素

力扣 215. 数组中的第K个最大元素
做法1:建大堆(把数组所有的数全放进去)，把前k-1个堆顶都踢了
做法二:建k个元素的小堆,先放k个进去,数组的其他的数遍历;如果比堆顶大，就放进去;
遍历完后,堆顶就是第k大的数
注意:建小堆要用greater

代码展示:class Solution {public: int findKthLargest(vector<int>& nums, int k) { priority_queue<int>pq; for(auto e:nums) { pq.push(e); } while(k>1) { pq.pop(); k--; } return pq.top(); }};

仿函数比起一般函数具有很多优点，以下描述错误的是©
A.在同一时间里，由某个仿函数所代表的单一函数，可能有不同的状态
B.仿函数即使定义相同，也可能有不同的类型
C.仿函数通常比一般函数速度快
D.仿函数使程序代码变简单

一下说法正确的是©
A.deque的存储空间为连续空间
B.list迭代器支持随机访问
C.如果需要高效的随机存取，还要大量的首尾的插入删除则建议使用deque
D.vector容量满时，那么插入元素时只需增加当前元素个数的内存即可

假设cont是一个Container 的示例，里面包含数个元素，那么当CONTAINER为： 1.vector 2.list 3.deque 会导致下面的代码片段崩溃的Container 类型是（C）int main(){Container cont = { 1, 2, 3, 4, 5};Container::iterator iter, tempIt;for (iter = cont.begin(); iter != cont.end();){ tempIt = iter;++iter;cont.erase(tempIt);}}A.1, 2B.2, 3C.1, 3D.1, 2, 3原因:vector和deque底层是连续空间，删除会挪动数据，最终导致iter意义变了

逆波兰表达式

引申:逆波兰表达式也叫做后缀表达式–也就是操作数顺序不变，操作符按优先级重排

举例如下:

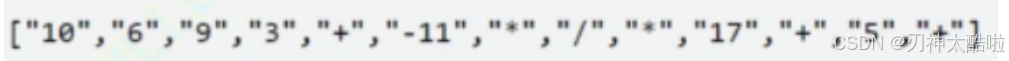
中缀表达式(平时的写法就是这个)转化为后缀表达式的方法:

一.遇到操作数就输出

二.操作符:

a.栈为空或当前操作符比栈顶的优先级高，这个操作符就入栈

b.栈不为空或当前操作符比栈顶的优先级低或者相等,就输出栈顶操作符

表达式结束后，依次出栈里面的操作符

注意:遇到左括号的话就递归，遇到右括号停止递归

这里的递归是:

遇到左括号时，把左括号当做新的起点，遇到右括号时就一直出栈，直到出到左括号为止

引申

自己搞的头文件里面没展开命名空间的话，在.cpp里面要在自己头文件之前展开命名空间才行，不然会报错

比如: using namespace std;#include \"text.h\"

在堆上开辟的空间的地址是随机的,没有地址先开就在前面的这些规定,栈就不一样