文章阅读非线性Non-Linearities In Atomic Quantum Receivers: Harmonic And Intermodulation Distortion
总括
Non-Linearities In Atomic Quantum Receivers: Harmonic And Intermodulation Distortion
我们将原⼦外差接收器中的这些差异归因于量⼦ Rydberg EIT 系统中存在的⾮线性响应和多波混频效应,预计这些效应会表现出与传统射频电⼦学的偏差。从拟合开始,我们测得 IP3= 2.7 dBV/m。必须强调的是,这些额外的峰值不是由检测中或接收器后端的任何电⼦伪影引起的。相反,它们只是作为原⼦本⾝的⾼阶效应出现的。在 RF 外差测量中,原⼦会受到来⾃ LO 和信号(Fand F) 场的 RF 电场。 根据⾃由空间中电磁学的叠加原理,由多个场分量引起的电场振幅是所有分量的线性和。通常情况下,谐波产⽣和 IMD 是由于元件(可能是⼆极管、放⼤器或接收器系统)在⾼电场下的⾮线性响应⽽产⽣的。在⽬前的情况下,正是原⼦ EIT 介质对电场的⾮线性响应导致了谐波产⽣和 IMD。
经典混频器
混频器的谐波分析
混频器是射频和微波系统中关键的组件,用于实现频率转换(如将高频信号下变频到中频)。其非线性特性会导致输入信号的频率成分互相调制,产生新的频率分量,包括基波、谐波和交调产物。以下是对混频器谐波分析的详细说明:
1. 混频器的非线性特性与谐波产生

2. 主要谐波分量及其影响

3. 谐波分析的数学方法
(1) 泰勒级数展开法
假设混频器的非线性特性可用泰勒级数近似: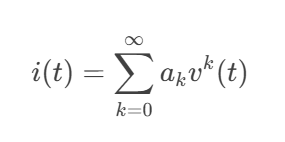
通过展开输入信号并提取各阶项,可解析计算各谐波分量的幅度。
(2) 转换矩阵法
适用于周期性大信号(如本振LO)驱动下的混频器,将非线性时变系统等效为线性时不变网络,通过矩阵计算谐波响应。
(3) 频谱仿真
使用电路仿真工具(如ADS、SPICE)进行时域-频域联合仿真,直接观察输出频谱中的谐波成分。
4. 谐波抑制技术
5. 实际测试与指标
(1) 谐波功率比(Harmonic Power Ratio)
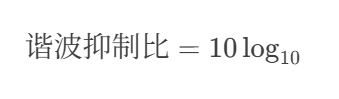
- 典型值:二次谐波抑制需优于-30 dBc,三次谐波优于-40 dBc。
(2) 测试步骤
- 输入信号:注入LO和RF信号。
- 频谱分析:用频谱仪测量输出端频谱,识别(\\omega_{\\text{IF}} = \\omega_{\\text{LO}} \\pm \\omega_{\\text{RF}}})及谐波分量。
- 功率计算:记录基波与各次谐波的功率值,计算抑制比。
6. 设计实例:双平衡混频器的谐波特性
- 结构:由四个二极管组成的环形混频器,本振(LO)和射频(RF)信号通过变压器耦合。
- 优势:
- 抑制偶次谐波(如(2\\omega_{\\text{LO}}}), (2\\omega_{\\text{RF}}}))。
- 高端口隔离度(LO-RF > 30 dB)。
- 谐波特性:
- 主要谐波为奇次((3\\omega_{\\text{LO}}}), (3\\omega_{\\text{RF}}})等)。
- 通过巴伦(Balun)和滤波进一步优化。
7. 总结
- 关键点:混频器的谐波由非线性特性引起,需通过数学建模、仿真和实测分析。
- 设计目标:在保证变频效率的同时,最大限度抑制谐波(尤其是二次和三次)。
- 趋势:集成化混频器(如Gilbert Cell)结合数字预失真(DPD),可进一步提升谐波抑制能力。
里德堡原子非线性响应
对原子接收器非线性行为研究的分析
1. 实验目的
该研究旨在通过单音测试(Single-Tone Measurement)系统表征原子接收器在射频(RF)信号作用下的非线性行为,包括谐波失真(Harmonic Distortion)和压缩点(P1dB)、截距点(IP2/IP3)等关键性能参数,以验证其与传统电子接收器的非线性响应差异。
2. 实验设计与方法

3. 实验结果与关键发现

4. 非线性机制解析

5. 技术意义与应用潜力

6. 局限性与未来方向
- 带宽限制:原子跃迁的自然线宽限制了工作带宽,需通过多原子混合或动态调谐扩展频段。
- 环境敏感性:原子气室对温度、磁场的稳定性要求较高,需开发鲁棒封装技术。
- 功率处理能力:高场强可能导致原子电离,需优化功率管理策略。
总结
该工作通过单音测试系统揭示了原子接收器的非线性行为,验证了其谐波生成机制与传统电子器件的本质差异。实验结果表明,原子接收器在可控场强下表现出可预测的非线性响应(如谐波斜率接近理论值),并具备抑制高阶失真的潜力。这一特性为安全通信、射频指纹识别等应用提供了物理层新思路,但需进一步解决带宽与环境稳定性问题以实现工程化应用。
双音非线性
对原子接收器互调失真研究的详细分析
1. 实验设计与配置
- 双音信号设置:

2. 数据呈现与关键结果
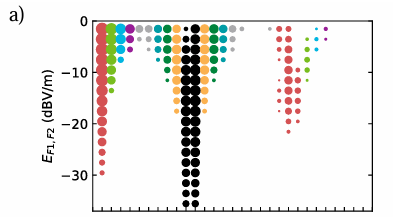
(1) IMD图谱(图4a)
-
图谱结构:
- 横轴:中频范围(10 kHz至300 kHz),覆盖基频与高阶互调产物。
- 纵轴:施加的射频电场强度(( E_1 = E_2 ))。
- 点表示:每个点对应检测到的频谱峰值,大小表示相对信号强度,颜色标记不同阶数的IMD:
- 黑色:基频(( f_1 )、( f_2 ))。
- 红色:二阶IMD(( N=2 ))。
- 黄色:三阶IMD(( N=3 ))。
- 绿色/青色/紫色:四阶(( N=4 ))、五阶(( N=5 ))、六阶(( N=6 ))、八阶(( N=8 ))IMD。
- 灰色:八阶以上IMD。
-
观察现象:
- 随着电场强度增加,高阶IMD逐渐显现,且高阶产物(如八阶)在强场下出现。
- 颜色分布:低阶IMD(如二阶、三阶)在低场强时即存在,高阶IMD需要更高场强激发。
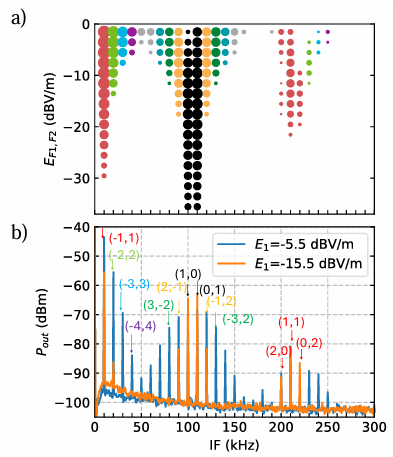
(2) 频谱响应示例(图4b)
- 选取场强切片:
- 低场强:仅基频和低阶IMD可见(如二阶、四阶)。
- 高场强:高阶IMD(如八阶)显著增强。


(3) 信号强度与场强关系(图4c)
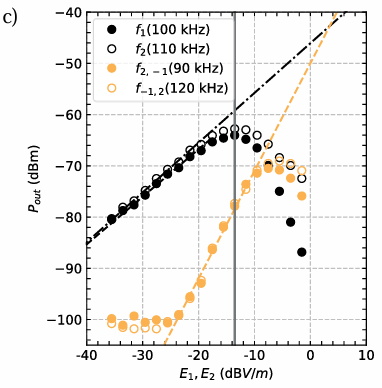


3. 物理机制解析

(1) 原子介质的非线性来源

(2) IMD抑制的量子特性
- 窄带滤波效应:
- 里德堡跃迁的自然线宽(MHz级)形成物理带通滤波器,抑制带外能量的输入,减少互调产物生成。
- 可控非线性响应:
- 通过调节EIT光强、原子密度等参数,可动态调整非线性阈值,实现IMD的人为控制。
4. 技术意义与性能优势

5. 实验验证与局限性
-
验证IMD来源:
- 确认互调产物源自原子非线性响应,而非后端电子噪声(如放大器失真)。
- 通过电场标定(基于里德堡原子)确保测量准确性。
-
局限性:
- 带宽限制:原子自然线宽限制工作频段,需多原子混合或动态调谐扩展。
- 功率处理能力:高场强可能引发原子电离,需优化功率管理策略。
6. 总结
该研究通过高精度双音测试,揭示了原子接收器在互调失真(IMD)行为上的独特优势:
- 非线性抑制:量子机制导致IMD斜率低于经典系统,减少带内干扰。
- 高线性度:宽动态范围和高压缩点(P1dB)支持强信号处理。
- 物理层可控性:通过调节原子参数实现IMD动态调控,为安全通信和射频指纹识别提供新途径。
对原子接收器互调失真研究的详细分析

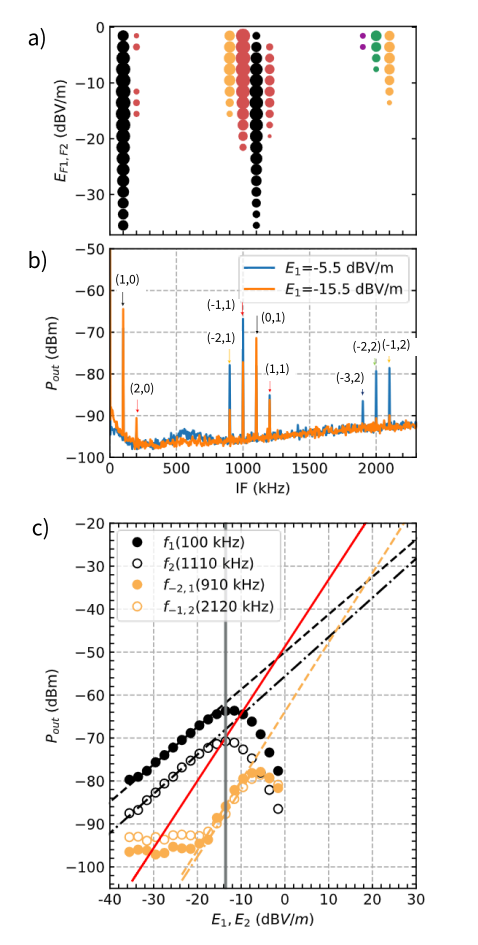



4. 技术意义与性能优势
高线性动态范围:
-
高IP3值(19.3 dBV/m)表明原子接收器在大信号输入下仍保持低失真,适用于高功率射频环境。
-
低IMD斜率(1.6)减少了带内干扰,提升信噪比(SNR)和系统灵敏度。
抗干扰能力:
- 原子IF带宽的窄带滤波特性(MHz级)天然抑制带外信号的IMD生成,增强抗邻道干扰(ACI)能力。
量子特性应用:
- 通过调节EIT光强或原子密度,可动态控制非线性响应,为物理层加密(如射频指纹)提供新手段。

6. 局限性与未来方向
-
带宽限制:原子自然线宽限制工作频段,需通过多原子集成或斯塔克调谐扩展。
-
环境敏感性:原子气室需严格控温、控磁,影响实际部署的鲁棒性。
-
功率处理:高场强可能引发原子电离,需优化场强管理策略。
总结
-
该研究通过对比不同频率间隔下的互调失真行为,揭示了原子接收器的量子非线性特性:
-
IMD斜率降低:量子相干性与带外衰减共同抑制非线性效率,斜率远低于经典系统。
-
高IP3与动态范围:宽线性工作区支持高功率输入,适用于抗干扰通信。
-
频率选择性优势:窄带原子滤波天然抑制带外干扰,提升信号纯净度。
对原子接收器与经典LNA互调失真性能对比的详细分析




5. 技术意义与应用潜力
• 高灵敏度通信:
低噪声基底与高SFDR使其适用于弱信号探测(如深空通信、量子雷达)。
• 抗干扰系统:
宽线性范围(FoM=35 dB)支持密集信号环境(如5G基站、军事电子战)。
• 安全通信:
利用IMD频谱的唯一性,实现物理层加密或射频指纹识别。

6. 局限性与未来方向
• 带宽限制:
原子自然线宽(MHz级)限制工作频段,需通过多原子集成或动态调谐扩展。
• 环境敏感性:
原子气室需精密控制温度、磁场,实际部署中需封装与稳定技术。
• 工程化挑战:
光学读取系统(如激光器、光电探测器)的微型化与成本控制。

总结
该研究通过量化SFDR(58 dB)与FoM(35 dB),揭示了原子接收器在互调失真性能上对经典LNA的显著优势,其核心源于量子机制的低噪声基底、高线性度及可控非线性响应。这些特性使其在抗干扰通信、高灵敏度传感和安全加密领域具有广阔应用前景,但需进一步解决带宽限制与环境鲁棒性问题以实现实际部署。
以下是对该部分工作的结构化分析:
1. 核心性能指标的定义与计算
• 无杂散动态范围(SFDR):
• 公式:( \\text{SFDR} = \\frac{2}{3} (\\text{IP3}_{\\text{out}} - N_0) )
• 参数来源:
◦ \\( \\text{IP3}_{\\text{out}} = -34 \\, \\text{dBm} \\)(三阶截止点输出功率,从图5c纵轴读取)◦ \\( N_0 = -121 \\, \\text{dBm} \\)(噪声基底,1 Hz分辨率带宽下的测量值)• 计算结果:( \\text{SFDR} = \\frac{2}{3} (-34 - (-121)) = 58 , \\text{dB} )
• 意义:SFDR衡量接收器在噪声基底以上无显著失真的最大动态范围,值越高表明抗干扰能力越强。
• 失真品质因数(FoM):
• 定义:( \\text{FoM} = \\text{IP3} - \\text{P1dB} )(输入功率层面,IP3和P1dB均取自图5c横轴)
• 原子接收器结果:( \\text{FoM} \\approx 35 , \\text{dB} )
• 经典LNA对比:典型FoM ≤ 12 dB(如Mini-Circuits ZX60-06183LN+等)
• 意义:FoM越大,表明接收器在压缩点前能容忍更强的信号而不引发显著三阶失真,抗干扰能力更优。
2. 量子与经典系统的性能对比
• 原子接收器优势:
• FoM显著更高(35 dB vs. 12 dB):量子系统在相同压缩点下,三阶失真出现更晚,动态范围更宽。
• 潜在原因:
◦ 非线性机制差异:里德堡原子的多波混频效应导致非线性响应斜率低于经典器件(如三阶IMD斜率2.1 vs. 3),延迟了失真阈值。◦ 量子噪声特性:原子系统的噪声基底可能更低,但此处未直接比较,需结合具体实验条件。• SFDR的适用性:
• 量子接收器的SFDR=58 dB虽未直接与LNA对比,但高FoM暗示其在大信号干扰下的稳健性更优。
3. 实验比较的关键区别与局限性
• 信号类型差异:
• 原子接收器:直接检测自由空间射频电场(如通过里德堡原子的电磁感应透明变化)。
• 经典LNA:处理导线中的电子信号,需通过天线转换自由空间场为电压信号。
• 影响:FoM比较未考虑天线增益或阻抗匹配,实际应用中天线性能可能影响绝对信号转换效率。
• 指标相对性:
• FoM为相对指标:仅反映输入功率层面的失真容忍度,未统一信号场强(如dBV/m vs. dBm)。
• 绝对性能对比的挑战:需假设天线参数(如有效孔径)才能统一量纲,而天线设计多样性导致难以标准化。
4. 技术意义与应用潜力
• 抗干扰能力:
• 原子接收器在存在强邻近干扰信号时(如通信频段拥挤场景),可能更不易被三阶失真淹没。
• 高灵敏度与非线性协同:
• 里德堡原子的高电场灵敏度(可达μV/m级)与独特非线性结合,或适用于弱信号探测中的复杂电磁环境。
• 潜在应用场景:
• 雷达与通信:在密集信号环境中提升信号分辨能力。
• 射频传感:用于电磁兼容性(EMC)测试或频谱监测,识别微小失真。
5. 未解决的问题与未来方向
• 量化转换因素:
• 如何将自由空间场强(dBV/m)与LNA的输入电压(dBm)公平对比?需建立包含天线效率的联合模型。
• 动态范围的实际限制:
• 原子接收器的P1dB压缩点较低(约-15.5 dBV/m),可能限制其处理强信号的能力,需优化原子密度或EIT参数以扩展线性区。
• 环境因素影响:
• 温度、原子碰撞等因素是否影响IMD特性?需进一步研究环境鲁棒性。
结论
该工作通过定义FoM和SFDR,首次系统量化了量子接收器在IMD性能上超越经典LNA的潜力。尽管存在信号类型和指标相对性的差异,35 dB的FoM和58 dB的SFDR仍凸显了里德堡原子系统在抗干扰和高动态范围场景的应用前景。未来需结合天线模型和实际环境测试,推动量子射频技术走向实用化。


