借助Leetcode 热门题目学习C++系列——原地算法_矩阵置零原地算法

技术文档

借助Leetcode 热门题目学习C++系列——原地算法

文章目录

借助Leetcode 热门题目学习C++系列——原地算法
- 1. 题目内容——矩阵置零
- 2. 原地算法
- 3. 代码实现
- - `vector<vector>& matrix`
  - 1. `vector`
  - 2. `vector<vector>`
  - 3. 传值和引用
  - 4. Vector 的特性
  - 5. 基本操作

1. 题目内容——矩阵置零

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法。
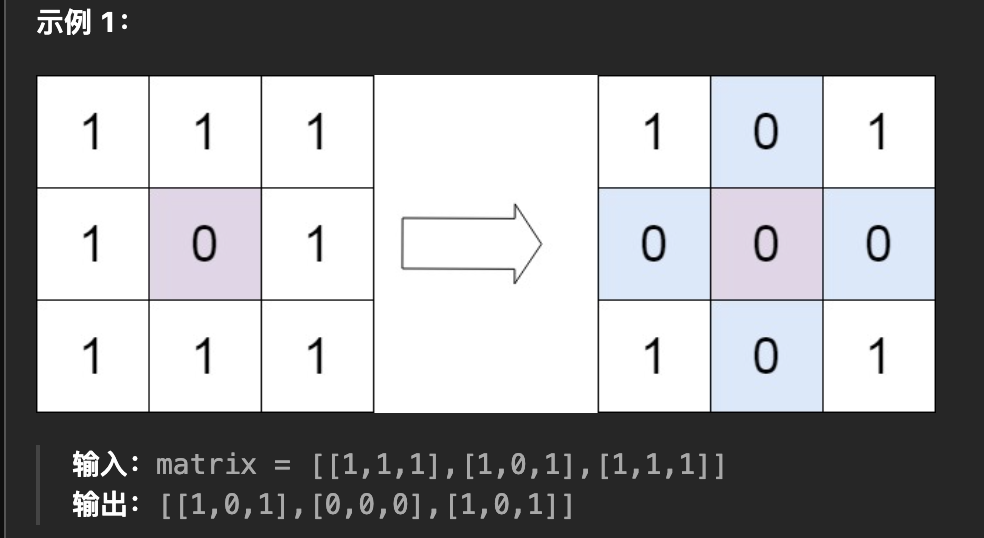
借助Leetcode 热门题目学习C++系列——原地算法_矩阵置零原地算法
看起来很简单的任务，对吧？但是这题让我觉得有趣的地方在于——原地算法。

2. 原地算法

原地算法是什么？

原地算法（in-place algorithm ）是一种使用小的，固定数量的额外空间来转换资料的算法。当算法执行时，输入的资料通常会被要输出的部份覆盖掉。

在计算复杂性理论中，原地算法包含使用 $O (1)$ 空间复杂度的所有算法。

通俗地说，就是求解问题只在原数据结构上进行，基本不需要额外的空间进行处理，输出之前会对输入的数据结构内容进行修改。本题也是一个道理，我需要直接输出置零的结果。因此不难得知，新建一个同样巨大的矩阵实际上并不被允许。

这道题的魅力，在我看来，是在我已经成功用 $O (m + n)$ 的额外空间轻松实现后，没想到这题甚至可以用 $O (1)$ 的额外开销实现。

3. 代码实现

下面是我最初的想法：

用一个col和row数组，提前记录是否存在元素为0的情况。例如：第i行第j列的元素为0，则记录row[i] 和col[j]为真。
遍历我们的两个信息数组，只要是第i行或者第j列为0，则相应元素直接置零。

那可能有疑问了，为什么不直接遇到一个0就直接把对应行列全处理呢？

答案是，会引入新的本不该为0的元素，我想，最后的结局就是，整个矩阵都变成了0。同时，不做任何记录会使在对某一行（或一列）做置零时将矩阵原来的0元素位置信息丢失，导致置零处理出现遗漏。

class Solution {public: void setZeroes(vector<vector<int>>& matrix) { int m = matrix.size(); int n = matrix[0].size(); vector<int> row(m), col(n); for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { if (!matrix[i][j]) {  row[i] = col[j] = true; } } } for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { if (row[i] || col[j]) {  matrix[i][j] = 0; } } } }};

上面是 $O (m + n)$ 的额外开销的实现。

但是，最妙的是，只用了两个额外变量的记录：

flag_col0和 flag_row0，分别表示第一列和第一行是否存在0元素。

思路如下：

flag_col0和 flag_row0的计算
遍历剩下的行列，并将是否出现零的逻辑结果存放在第一行和第一列中（原地算法的精妙）
依照第一行和第一列以及两个记录值flag_col0和 flag_row0对矩阵进行置零处理。

问题又来了，第一行用来存结果，那它自己的信息怎么办？不会被改动和覆盖吗？
实际上，由于我只在第i行出现0元素的情况下，才会修改matrix[i][0]，而此时这个值不再有存在的必要（因为马上在第三步会被置零）。

class Solution {public: void setZeroes(vector<vector<int>>& matrix) { int m = matrix.size(); int n = matrix[0].size(); int flag_col0 = false, flag_row0 = false; for (int i = 0; i < m; i++) { if (!matrix[i][0]) { flag_col0 = true; } } for (int j = 0; j < n; j++) { if (!matrix[0][j]) { flag_row0 = true; } } for (int i = 1; i < m; i++) { for (int j = 1; j < n; j++) { if (!matrix[i][j]) {  matrix[i][0] = matrix[0][j] = 0; } } } for (int i = 1; i < m; i++) { for (int j = 1; j < n; j++) { if (!matrix[i][0] || !matrix[0][j]) {  matrix[i][j] = 0; } } } if (flag_col0) { for (int i = 0; i < m; i++) { matrix[i][0] = 0; } } if (flag_row0) { for (int j = 0; j < n; j++) { matrix[0][j] = 0; } } }};

既然是学习C++，那就理解一下——

`vector<vector>& matrix`

vector 是 C++ 标准模板库（STL）的一部分，是一种序列容器，它允许你在运行时动态地插入和删除元素。
vector 是基于数组的数据结构，但它可以自动管理内存，这意味着你不需要手动分配和释放内存。

1. `vector`

表示一个一维的整型动态数组：

vector<int> row = {1, 2, 3};

2. `vector<vector>`

表示一个二维的整型动态数组，也就是一个矩阵：

vector<vector<int>> matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9}};

3. 传值和引用

传值：复制一份数据，原矩阵不变

void func(vector<vector<int>> matrix);

引用：共享数据，原矩阵会被修改

void func(vector<vector<int>>& matrix);

4. Vector 的特性

动态大小：vector 的大小可以根据需要自动增长和缩小。
连续存储：vector 中的元素在内存中是连续存储的，这使得访问元素非常快速。
可迭代：vector 可以被迭代，可以使用循环（如 for 循环）来访问它的元素。
元素类型：vector 可以存储任何类型的元素，包括内置类型、对象、指针等。

5. 基本操作

#include

创建 Vector
创建一个 vector 可以像创建其他变量一样简单：

std::vector<int> myVector; // 创建一个存储整数的空 vector

可以使用 push_back 方法向 vector 中添加元素：

myVector.push_back(7); // 将整数 7 添加到 vector 的末尾

访问元素
可以使用下标操作符 [] 或 at() 方法访问 vector 中的元素：

int x = myVector[0]; // 获取第一个元素int y = myVector.at(1); // 获取第二个元素

获取大小
可以使用 size() 方法获取 vector 中元素的数量：

int size = myVector.size(); // 获取 vector 中的元素数量

迭代访问
- 可以使用迭代器遍历 vector 中的元素，或者使用范围循环：

for (auto it = myVector.begin(); it != myVector.end(); ++it) { std::cout << *it << \" \";}

for (int element : myVector) { std::cout << element << \" \";}

删除元素
可以使用 erase() 方法删除 vector 中的元素：

myVector.erase(myVector.begin() + 2); // 删除第三个元素

清空 Vector
可以使用 clear() 方法清空 vector 中的所有元素：

myVector.clear(); // 清空 vector

借助Leetcode 热门题目学习C++系列——原地算法_矩阵置零原地算法