空间组合与像素蔓延:硬币动态规划与颜色填充的算法二重奏
在算法宇宙的对立两极,离散数学与连续空间奏响奇妙的交响。当硬币在组合数学中碰撞出无限可能,当颜色在像素网格中如水银泻地般蔓延,两种看似无关的挑战在\"状态演化\"的哲学层面共振。今日,我们将深入两个经典问题:硬币表示法(Coin Change)与颜色填充(Flood Fill)。一个在离散整数域探索组合爆炸,一个在连续像素空间实现区域生长。跟随本文,您将掌握完全背包动态规划与图遍历扩散的思维框架,体验从数论到拓扑学的思维跃迁!
问题一:硬币表示法——离散组合的完全背包艺术
硬币。给定数量不限的硬币,币值为25分、10分、5分和1分,编写代码计算n分有几种表示法。(结果可能会很大,你需要将结果模上1000000007)
问题本质
给定无限供应的四种面额硬币(25/10/5/1分),计算组成金额 $n$ 的独特组合方式数量(模 $10^9+7$)。
示例解析
n=10 → 4种表示法:1. 10(单枚10分)2. 5+5(两枚5分)3. 5+1×5(一枚5分+五枚1分)4. 1×10(十枚1分)
算法策略:动态规划与完全背包优化
-
状态空间建模:
-
$dp[i]$:组成金额 $i$ 的组合数
-
初始状态:$dp[0]=1$(零金额存在空解)
-
-
状态转移方程:
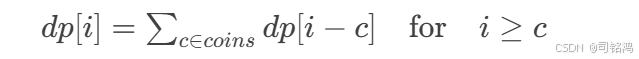
-
组合去重优化:
-
有序枚举原则:按面额降序(25→10→5→1)处理硬币
-
状态转移约束:当前硬币面额 $\\leq$ 目标金额时才转移
-
-
模运算处理:
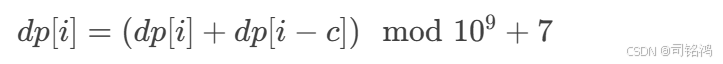
数学本质
问题等价于求解丢番图方程:
25x+10y+5z+w=n(x,y,z,w∈N)25x+10y+5z+w=n(x,y,z,w∈N)
的解空间基数,属组合数论范畴。
复杂度优化
-
空间压缩:使用滚动数组将空间复杂度降至 $O(n)$
-
时间优化:$O(n \\cdot |coins|)$,$|coins|=4$ 即 $O(4n)$
示例推演(n=5)
初始化:dp = [1,0,0,0,0,0]处理5分: dp[5] += dp[0] → dp[5]=1处理1分: dp[1] += dp[0] → 1 dp[2] += dp[1] → 1 dp[3] += dp[2] → 1 dp[4] += dp[3] → 1 dp[5] += dp[4] → 1+1=2最终:dp[5]=2
题目程序:
#include // 包含标准输入输出库#include // 包含动态内存分配和程序退出函数#define MOD 1000000007 // 定义模数常量,10^9+7int main() { // 主函数入口 int n; // 声明目标金额变量n // 提示用户输入金额n printf(\"Enter the amount in cents (n): \"); // 读取用户输入的整数并存储到n if (scanf(\"%d\", &n) != 1) { // 如果读取失败 // 打印错误信息 printf(\"Invalid input. Please enter an integer.\\n\"); return 1; // 非正常退出程序 } if (n < 0) { // 检查输入是否为负数 // 打印错误信息 printf(\"Error: Amount cannot be negative.\\n\"); return 1; // 非正常退出程序 } // 动态分配dp数组,大小为n+1(包含0到n) int *dp = (int*)calloc(n + 1, sizeof(int)); if (dp == NULL) { // 检查内存分配是否成功 // 打印内存分配失败信息 printf(\"Memory allocation failed.\\n\"); return 1; // 非正常退出程序 } dp[0] = 1; // 初始化dp[0]=1(表示金额0有1种组合:空组合) // 定义硬币面额数组(按降序排列:25,10,5,1) const int coins[] = {25, 10, 5, 1}; // 计算硬币种类数量(4种) const int num_coins = sizeof(coins) / sizeof(coins[0]); // 外层循环:遍历每种硬币(从最大面额到最小) for (int i = 0; i < num_coins; i++) { int coin = coins[i]; // 获取当前硬币面额 // 内层循环:从当前硬币面额开始,更新到目标金额n for (int j = coin; j <= n; j++) { // 状态转移:dp[j] = dp[j] + dp[j-coin] dp[j] = (dp[j] + dp[j - coin]) % MOD; } } // 输出结果:组成金额n的组合数(模10^9+7) printf(\"Number of unique combinations: %d\\n\", dp[n]); free(dp); // 释放动态分配的dp数组内存 return 0; // 程序正常退出}输出结果: 
问题二:颜色填充——连续空间的图遍历扩散
编写函数,实现许多图片编辑软件都支持的「颜色填充」功能。
待填充的图像用二维数组 image 表示,元素为初始颜色值。初始坐标点的行坐标为 sr 列坐标为 sc。需要填充的新颜色为 newColor 。
「周围区域」是指颜色相同且在上、下、左、右四个方向上存在相连情况的若干元素。
请用新颜色填充初始坐标点的周围区域,并返回填充后的图像。
问题定义
在二维像素矩阵 $image$ 中,从种子点 $(sr,sc)$ 开始,将与种子点颜色相同且四连通的区域填充为 $newColor$。
示例解析
输入: [[1,1,1], [1,1,0], [1,0,1]] 种子点(1,1),新颜色2输出: [[2,2,2], [2,2,0], [2,0,1]]
题目程序:
#include // 包含标准输入输出库#include // 包含动态内存分配和程序退出函数// 定义像素点结构体typedef struct { int x; // 像素的行坐标 int y; // 像素的列坐标} Point;// 定义最大栈大小(假设图像最大为100x100)#define MAX_STACK_SIZE 10000// 颜色填充函数void floodFill(int** image, int imageSize, int* imageColSize, int sr, int sc, int newColor) { // 获取种子点的原始颜色 int oldColor = image[sr][sc]; // 如果新颜色等于旧颜色,直接返回(无需填充) if (oldColor == newColor) { return; } // 创建栈用于存储待处理像素点 Point* stack = (Point*)malloc(MAX_STACK_SIZE * sizeof(Point)); // 初始化栈顶指针 int top = -1; // 将种子点压入栈 top++; stack[top] = (Point){sr, sc}; // 循环处理直到栈为空 while (top >= 0) { // 弹出栈顶像素点 Point p = stack[top]; top--; int x = p.x; int y = p.y; // 如果当前点颜色已改变,跳过处理 if (image[x][y] != oldColor) { continue; } // 向左扫描直到边界(相同颜色区域的最左端) int left = y; while (left >= 0 && image[x][left] == oldColor) { left--; } // 向右扫描直到边界(相同颜色区域的最右端) int right = y; while (right < imageColSize[x] && image[x][right] == oldColor) { right++; } // 填充当前扫描行(从left+1到right-1) for (int col = left + 1; col = 0 && image[x - 1][col] == oldColor) { // 将符合条件的点压入栈 top++; stack[top] = (Point){x - 1, col}; } // 检查下一行同列位置 if (x + 1 < imageSize && image[x + 1][col] == oldColor) { // 将符合条件的点压入栈 top++; stack[top] = (Point){x + 1, col}; } } } // 释放栈内存 free(stack);}// 打印图像矩阵void printImage(int** image, int rows, int cols) { for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { printf(\"%d \", image[i][j]); // 打印每个像素值 } printf(\"\\n\"); // 换行 }}int main() { // 设置图像参数 int rows = 3, cols = 3; // 动态分配图像内存 int** image = (int**)malloc(rows * sizeof(int*)); for (int i = 0; i < rows; i++) { image[i] = (int*)malloc(cols * sizeof(int)); } // 初始化图像数据 int data[3][3] = { {1, 1, 1}, {1, 1, 0}, {1, 0, 1} }; // 复制数据到图像矩阵 for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { image[i][j] = data[i][j]; } } // 设置每行列数(所有行相同) int* colSizes = (int*)malloc(rows * sizeof(int)); for (int i = 0; i < rows; i++) { colSizes[i] = cols; } // 打印填充前的图像 printf(\"Original image:\\n\"); printImage(image, rows, cols); // 执行颜色填充(种子点(1,1),新颜色2) floodFill(image, rows, colSizes, 1, 1, 2); // 打印填充后的图像 printf(\"\\nAfter flood fill:\\n\"); printImage(image, rows, cols); // 释放内存 for (int i = 0; i < rows; i++) { free(image[i]); } free(image); free(colSizes); return 0; // 程序正常退出}输出结果: 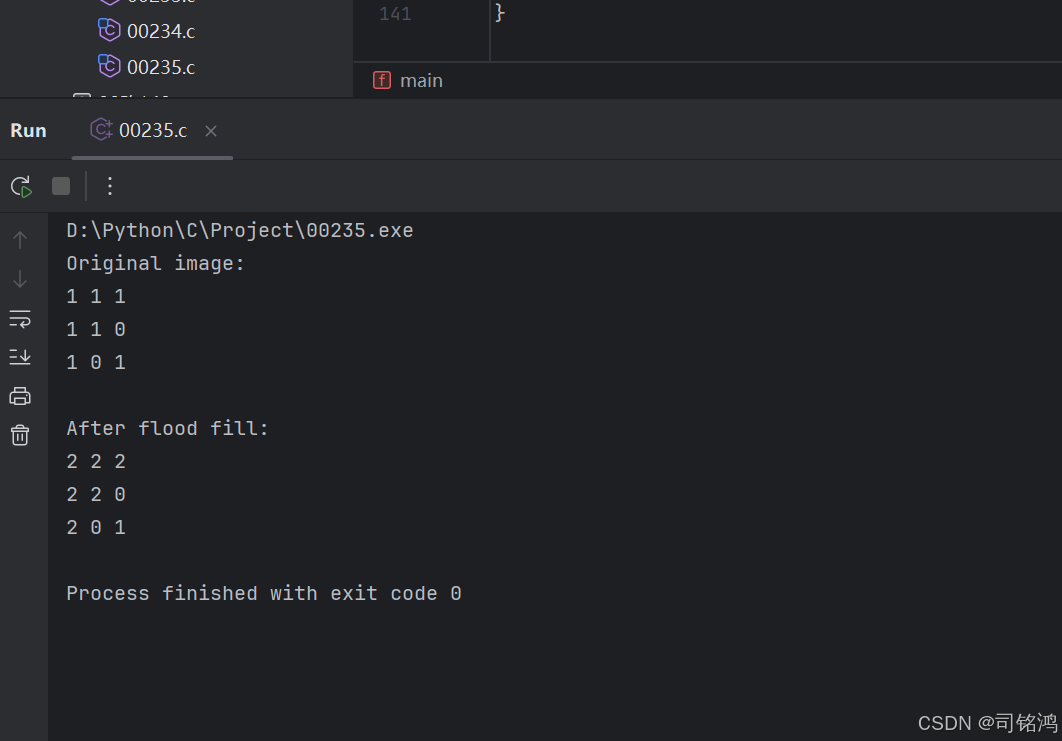
算法策略:多范式扩散模型
-
核心算法选择:
算法 空间复杂度 特点 BFS $O(\\min(m,n))$ 队列实现,辐射式扩散 DFS $O(mn)$ 递归实现,深度优先 扫描线 $O(1)$ 无递归栈,工业级方案 -
四连通向量:
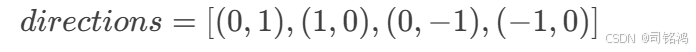
-
边界条件:
-
坐标合法性:$0 \\leq x < m,\\ 0 \\leq y < n$
-
颜色匹配:$image[x][y] == oldColor$
-
终止条件:遇到不同颜色或边界
-
扫描线填充优化(工业级实现)
def scanline_fill(sr, sc, newColor): oldColor = image[sr][sc] if oldColor == newColor: return stack = [(sr, sc)] while stack: x, y = stack.pop() # 向左填充至边界 l = y while l >= 0 and image[x][l] == oldColor: l -= 1 # 向右填充至边界 r = y while r 0 and image[x-1][i] == oldColor: stack.append((x-1, i)) if x < m-1 and image[x+1][i] == oldColor: stack.append((x+1, i))
算法对比:离散组合与连续扩散的辩证统一
哲学统一性
-
状态演化思想:
-
硬币:金额状态 $i$ 由 $i-c$ 演化而来
-
填充:像素状态由邻域状态传播而来
-
-
边界处理艺术:
-
硬币:金额边界 $i=0$ 作为初始状态
-
填充:图像边界与颜色突变作为终止条件
-
-
维度转换智慧:
-
硬币:将三维组合问题(面额×数量×金额)压缩为一维DP
-
填充:将二维连通问题分解为一维行扫描
-
结语:离散与连续的算法协奏曲
硬币表示法是组合数学在计算机科学的完美映射——它证明:通过动态规划的状态转移,无限组合可能性可被优雅地压缩进线性空间。颜色填充则是计算几何的经典实践,揭示了区域生长算法在像素拓扑中的普适性。
二者共同诠释算法设计的核心法则:
\"所有离散问题都有连续背景,
所有连续问题都有离散本质\"
—— 大卫·希尔伯特(数学巨匠)
在AI时代,这些思想延伸至:
-
区块链(硬币问题→UTXO模型优化)
-
计算机视觉(颜色填充→语义分割算法基础)
当您面对复杂系统时,请铭记:
-
硬币的启示:通过状态压缩驯服组合爆炸
-
填充的箴言:通过局部扩散实现全局变化
深度思考:
-
硬币DP的状态转移能否类比神经元激活机制?
-
颜色填充算法如何优化自动驾驶场景分割?
欢迎在评论区展开跨学科对话!


